并网逆变器输出LCL滤波器的优化设计

2015-01-03杨公德施火泉

电源学报 2015年1期

关键词：电感阻尼谐波

杨公德，施火泉，吴磊，王猛

（1.江南大学物联网工程学院，无锡 214122；2.广东工业大学自动化学院，广州 510006）

并网逆变器输出LCL滤波器的优化设计

杨公德1，施火泉1，吴磊1，王猛2

（1.江南大学物联网工程学院，无锡 214122；2.广东工业大学自动化学院，广州 510006）

具有优越滤波性能、易于集成和封装的LCL滤波器在分布式并网发电系统中的应用日益广泛，然而零阻尼引起的谐振问题不仅影响闭环控制系统的稳定性，而且导致入网电流性能降低。如何设计和优化滤波参数来提升LCL滤波器的滤波性能成为研究的热点。在滤波总电感和滤波电容满足系统性能的条件下，比较分析了电感分布系数和阻尼电阻对系统的稳定性、滤波效果、开关次谐波衰减比、阻尼值及阻尼损耗的影响，并在此基础上，给出了电感分布系数和阻尼电阻优化方法一般设计流程。仿真结果表明该优化方法是有效的。

LCL滤波器；电感分布系数；阻尼电阻；滤波效果；阻尼损耗

引言

分布式并网发电系统采用传统的大电感滤除电流中的开关次谐波来满足并网的相关标准，不仅会降低系统的动态性能，而且因其体积和重量较大而不易集成和封装。针对这个问题，许多文献提出采用较小电感和电容的LCL滤波器。尽管LCL滤波器抑制开关次谐波的效果优越，但其发生谐振时产生的零阻尼不仅影响闭环控制系统的稳定性，而且导致入网电流的性能降低［1］。因而如何设计和优化滤波参数来提升LCL滤波器的滤波性能成为研究的热点。文献［2-4］给出了滤波器设计的一般步骤，但没有讨论各个参数内在的联系及其对系统性能的影响，并且有些参数凭借经验方式给定；文献［5-8］探讨了各滤波参数之间的内在联系并且给出了部分约束条件的关系式，但仍需要多次尝试才能找到合适参数；文献［9］通过图解分析法设计和优化了滤波器参数，虽然直观，但当某一参数或指标变化时，结果就会不同，同时作图也较为复杂。

本文通过比较分析滤波参数对LCL滤波系统的稳定性、滤波效果、开关次谐波衰减比、阻尼值及阻尼损耗的影响，在综合各种约束条件的基础上提出一种滤波器优化设计方法，并通过仿真分析验证该方法的有效性。

1 LCL滤波器等效模型

依据LCL滤波单相桥式并网逆变器的拓扑结构得到的LCL滤波器等效模型［1］如图1所示。图中，L1为逆变器侧电感，L2为网侧电感，Cf为滤波电容，Rd为阻尼电阻。Ug为电网电压，Uinv为全桥逆变器输出交流电压。

图1 LCL滤波器等效模型Fig.1 Equivalent mode of LCL filter

令L1＋L2＝L，L1/L＝k，其中k为电感分布系数，L为总滤波电感。由图1可得到从Uinv、i1到ig的传递函数为

2 滤波参数对系统性能影响分析

在设计总滤波电感L时，既要满足并网电流的谐波指标，又要考虑并网电流跟踪电网电压的快速性要求；设计滤波电容时，既要考虑衰减高频谐波能力，又要使系统具有较高的效率。据此［2］本文设定L＝2.5 mH，Cf＝20 μF，分析电感分布系数k和阻尼电阻Rd对系统的稳定性、滤波效果、开关次谐波衰减比、阻尼值及阻尼损耗的影响。

2.1 滤波参数对系统稳定性影响分析

图2分别给出了式（1）不同k和Rd时所对应的零极点。由奈斯稳定判据可知随着Rd值的逐渐增大，系统的稳定性就相应地增加；由于k的对称性，在分析k对稳定性的影响时，仅分析其左半部分，当k值逐渐增大时，系统的稳定性却相应地减少。

图2 不同k和Rd所对应的零极点Fig.2 Zero-pole diagram of different k and Rd

2.2 k和Rd对系统滤波效果的影响分析

图3分别给出了式（1）中不同的k和Rd时所对应的Bode图。当k一定时，随着Rd的逐渐增大，虽对谐振峰起到很好的抑致作用，但系统的高频滤波效果逐渐变差；当Rd一定时，随着k值的增大，虽然其频率带宽有所降低，但其高频谐波的衰减速率较大。

图3 不同k和Rd时所对应的Bode图Fig.3 Bode diagram of different k and Rd

2.3 滤波参数对衰减比的影响分析

将从逆变器侧开关次谐波电流i1h到网侧开关次谐波电流igh的传递函数的幅值记为高次谐波衰减比D，即

式中，ωc为开关角频率。取开关频率为20 kHz。则D与k和Rd二维关系如图4所示。当Rd为定值时，D随着k值的增大而增加;而对于不同的Rd时，D都有一个由缓慢变化到快速变化的转折点，并且Rd越大，这个转折点越小；当k为定值且Rd较小时，D随Rd的增大而迅速增加；当Rd超过某一临界值后，D不再随Rd的变化而变化；对于不同的k，D都有一个由快速变化到几乎不变化的转折点，并且k越大，这个转折点就越小，同时其对应的阻尼值也比较小。

图4 不同的k和Rd所对应D的关系Fig.4 Relationship of different k and Rdcorresponding with D

2.4 滤波参数对系统阻尼值的影响分析

LCL滤波器必然存在谐振尖峰的主要原因是系统无阻尼值，通过在滤波电容支路串联电阻的方式可以增加系统的阻尼值，从而达到消除谐振尖峰而使系统稳定的目的。依据式（1）的第1个算式得到阻尼值ζ为

则ζ与k和Rd的二维关系如图5所示。当k为定值时，ζ和Rd呈线性关系，且ζ随着Rd的增大而增大；当k为不同的值时，其值越大，ζ的变化速率越小。当Rd为定值时，ζ随着k的增大先减小至最小值再由最小值继续增大，并且在k值的两端，ζ随k变化的速率较大；当Rd不同时，其值越大，ζ越大，并且在k值的两端，ζ随k变化的速率也在增大。

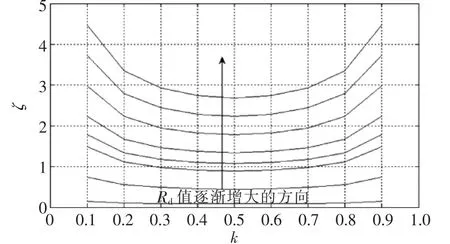
图5 不同k和Rd对应的ζ的关系Fig.5 Relationship of different k and Rdcorresponding with ζ

2.5 滤波参数对系统阻尼损耗的影响分析

电容支路串联的阻尼电阻可通过抑制谐振点来保障系统的稳定性，但同时也带来了阻尼损耗问题。如果对其处理不当，不仅会降低系统效率，也可能影响其他器件的性能而使系统的可靠性降低。因而串入电路的阻尼电阻在保证系统稳定的条件下，需尽可能小地降低系统的阻尼损耗。鉴于此，由式（1）和基本电流定律可得流过阻尼电阻的电流为

电流ic主要由开关整个频率次谐波电流、基波电流及谐振电流等三部分构成，由于滤波电容对基波的阻抗较大，因而对于基波电流而言，阻容支路可以看作开路。另外由于阻尼电阻对谐振峰的抑制作用，也可近似认为流过阻容支路的谐振电流为0。因而阻尼电阻的阻尼损耗主要源于开关频率次谐波电流，即

式中，Ih为谐波电流的有效值。由式（5）所得P与k和Rd的二维关系如图6所示。当k为定值时，P先随着Rd的增大而增大到最大值，随后再减小，并且功率增大的速率远大于功率减小的速率；当k逐渐增大时，出现转折时的Rd值越小。当Rd小于某一临界值时，P随k的增大开始时几乎保持不变，随后呈下降的趋势，并且k越大，P保持为恒定值的范围越小，功率下降速率越大；当Rd大于某一临界值时，P随k的增大而一直减小，并且k越大，P越小。

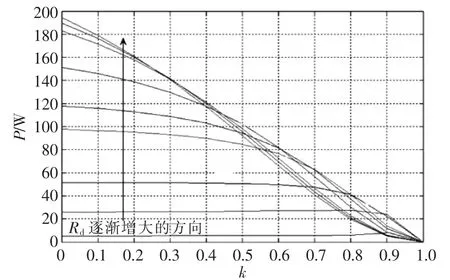
图6 不同k和Rd所对应的P的关系Fig.l Relationship of different k and Rdcorresponding with P

3 LCL滤波参数的优化

3.1 滤波参数优化过程

LCL滤波的并网逆变器对谐振频率的限制条件为10ω＜ωres＜0.5ωc，其中ω为电网角频率。依据此限制条件可知，能使系统稳定的k的取值范围为：0.099＜k＜0.283或0.717＜k＜0.911，且关于k＝0.5对称。由图5可知，串入滤波电容支路的阻尼电阻太小而使系统处于欠阻尼状态，仍会使系统出现谐振而不稳定，因而为了使系统具有较好的稳定性，本文选定阻尼值ζ≥0.5，则阻尼电阻Rd的范围为

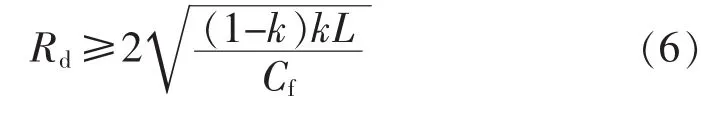
根据以上所得k的范围，并带入已知滤波参数值可得：Rd≥5.036 Ω。

k的取值需要满足开关次谐波衰减比的指标、一定的阻尼值及较小的阻尼损耗等约束条件。一般情况下开关次谐波衰减比小于20%。根据图4可知，Rd越大，则越不易满足开关次谐波衰减比的指标，故此要求Rd值不要太大，通过分析阻尼值和k的二维关系可知Rd值越大越易满足阻尼值ζ≥0.5的要求。而根据图6可知，在经过某一转折阻尼电阻后，功率损耗随着阻尼电阻的增大而减小，若求解的最小阻尼电阻在转折阻尼电阻的左侧时能使功率损耗最小，就选择这个最小的阻尼电阻作为设计值；若其值在右侧，则希望阻尼电阻值越大越好。综合考虑稳定性、滤波效果及功率损耗等因素，电感分布系数的取值最好在0.099～0.283之间，阻尼电阻的范围最好在最小阻尼电阻到转折阻尼电阻之间，尤其宜取最小阻尼电阻值。

3.2 滤波参数优化的一般方法

以上滤波器参数优化是基于L＝2.5 mH、Cf＝20 μF的情况进行分析的。对于在给定开关频率下工作的不同容量的逆变系统，当按照一般的步骤设计出满足系统性能要求的总滤波电感L和滤波电容Cf后，也可以按照以上分析方法对电感分布系数k和阻尼电阻Rd进行优化，其优化过程的流程如图7所示。

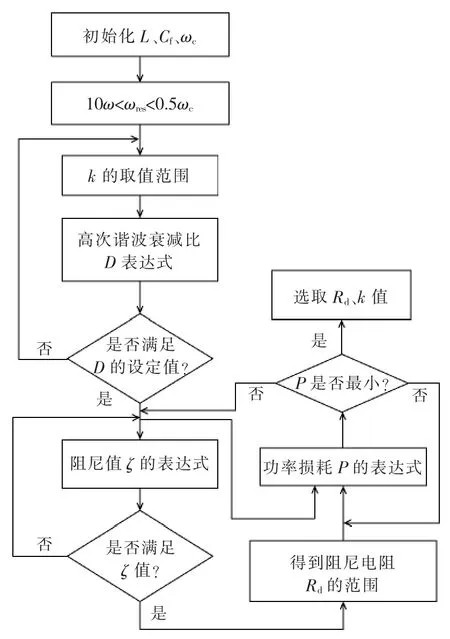
图7 k和Rd优化设计流程Fig.7 Flow chart of k and Rdoptimization design

4 仿真结果

为了验证所优化设计的滤波参数的有效性，依据LCL滤波单相并网逆变器控制框图，采用i1和ig的加权电流和电容电流的双闭环控制搭建了仿真模型［10-15］，如图8所示。其仿真参数为：直流母线电压Ud为400 V，开关频率为20 kHz，电网电压Ug为220 V/50 Hz。

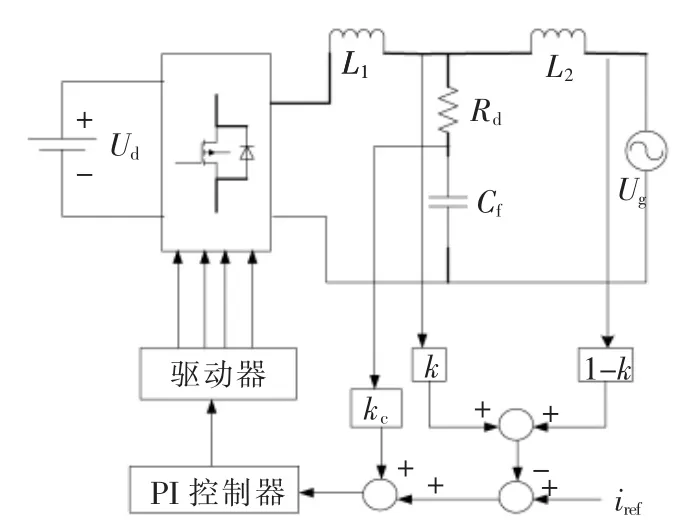
图8 LCL滤波单相桥并网逆变器的控制框图Fig.8 Control block diagram of single-phase bridge inverter connected-grid with LCL filter

当Rd为5.036 Ω，k分别为0.2、0.4和0.6时，逆变器侧电感电流、电容电流及网侧电流的仿真波形如图9所示。

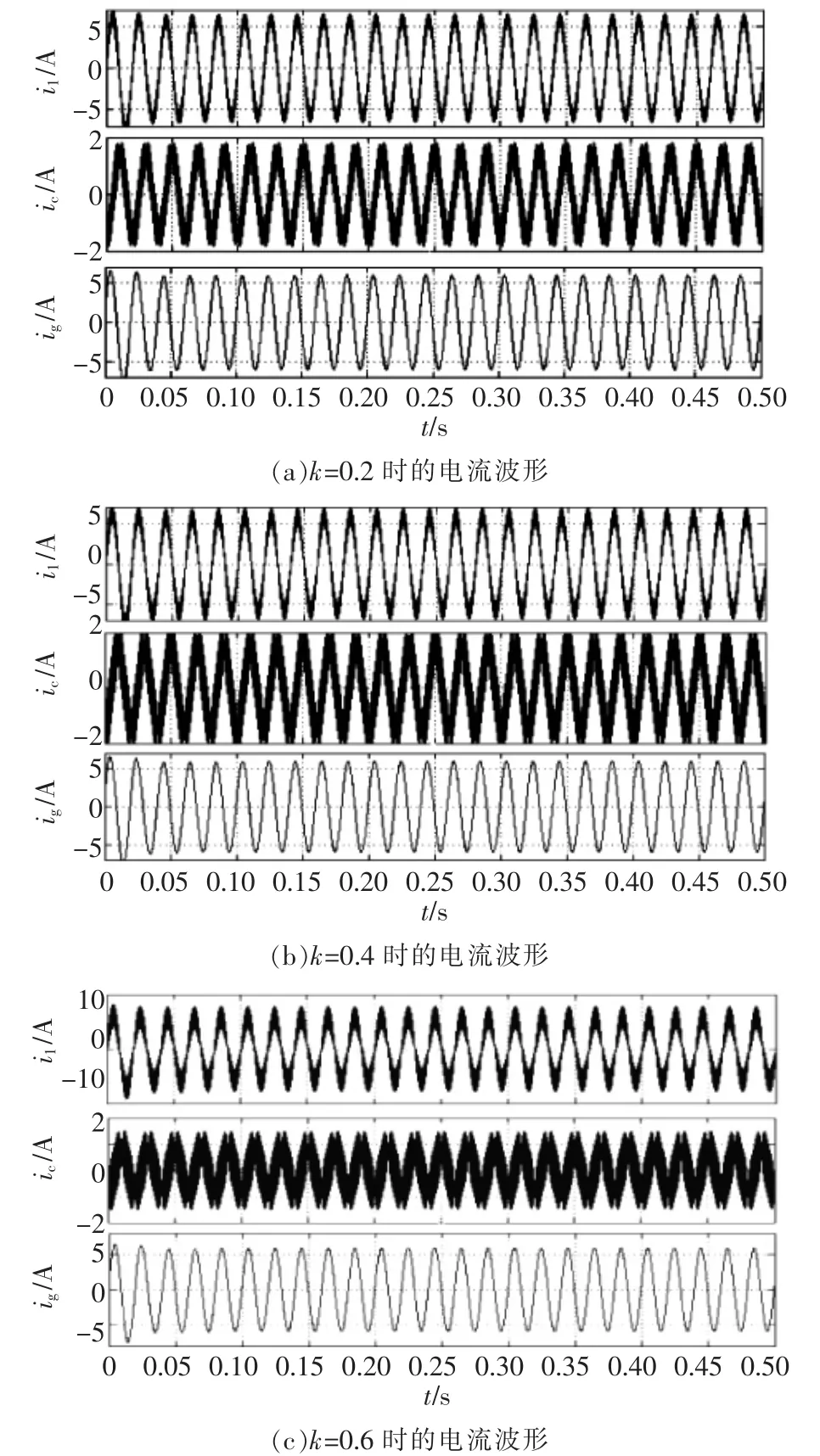
图9 逆变器输出电流波形Fig.9 Output current waveforms of inverter

为了定量比较分析本文优化方法的正确性和有效性，当电感分布系数k和阻尼电阻Rd不同时，逆变器侧电感电流、电容电流及网侧电感电流的谐波畸变率，开关次谐波衰减比、阻尼值和功率损耗分别如表1～表4所示。

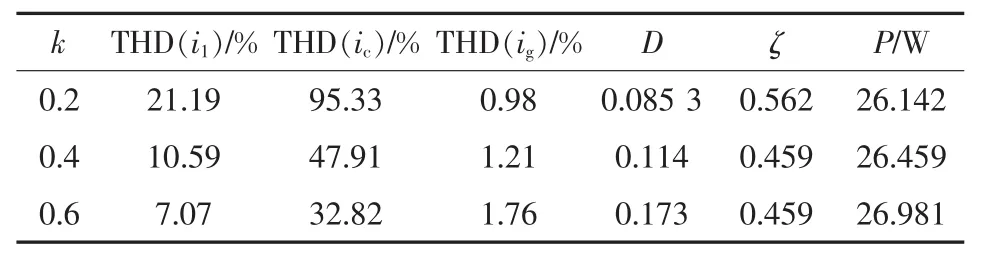
表1 Rd＝5.03 Ω时的性能指标Tab.1 Performance indexes when Rdis 5.03 Ω

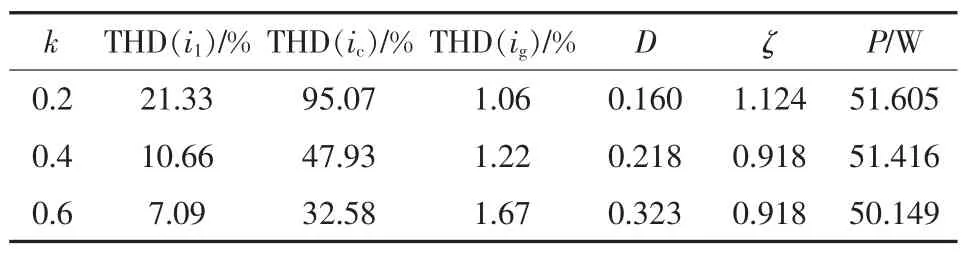
表2 Rd＝10 Ω时的性能指标Tab.2 Performance indexes when Rdis 10 Ω

表3 Rd＝15 Ω时的性能指标Tab.3 Performance indexes when Rdis 15 Ω

表4 Rd=200 Ω时的性能指标Tab.4 Performance indexes when Rdis 200 Ω

通过分析可知，表中的数据同以上分析和优化设计的结果相一致。

5 结语

本文在滤波总电感和滤波电容满足系统性能的条件下，比较分析了电感分布系数和阻尼电阻对系统的稳定性、滤波效果、开关次谐波衰减比、阻尼值及阻尼损耗的影响。在此基础上，通过综合考虑滤波参数和系统性能的内在关系，提出一种LCL滤波器的优化方法，并给出了一般设计流程，仿真结果表明了本文所优化的滤波参数的正确性和有效性。与传统滤波参数设计方法相比，此方案依据各种约束条件，通过编程建立一个可视化的操作界面，可以很方便地获得满足系统所需要的滤波参数，在工程上具有一定的应用价值。

［1］周克亮，王政，徐青山.光伏与风力发电系统并网变换器［M］.北京：机械工业出版社，2013：267-273.Zhou Keliang，Wang Zheng，Xu Qingshan.Grid Convertes for PV and Wind Power Systems［M］.Beijing：China Machine Press，2013.

［2］张宪平，李亚西，潘磊.三相电压型整流器的LCL型滤波器分析与设计［J］.电气应用，2007，26（5）：65-68.Zhang Xianping，Li Yaxi，Pan Lei.Analysis and design of LCL type filter for three-phase voltage source rectifier［J］.Electric Applications，2007，26（5）：65-68.

［3］Marco L，Fred B.Design and control of a LCL filter based three phase active rectifier［J］.IEEE Transactions on Industry Applications，2005，41（5）：1281-1290.

［4］Liserr，Fuchs.Filter-based active damping of v-oltage source converters with LCL filter［J］.IEEE Transactions on Industrial Electronics，2011，（55）：3623-3633.

［5］张勇.分布式发电系统中的LCL滤波器性能分析和设计［J］.电力电容器与无功补偿，2013，34（6）：29-32.Zhang Rong.LCL filter design and perfomance analysis for distributed generation system［J］.Power Capacitor＆Reactive Power Compensation，2013，34（6）：29-32.

［6］张国荣，李中均.并联有源电力滤波器中LCL滤波器的分析与设计［J］.高压电，2011，47（6）：19-28.Zhang Guorong，Li Zhongjun.Analysis and design of LCL-filter in shunt active power filter［J］.High Voltage Apparatus，2011，47（6）：19-28.

［7］王要强，吴凤江.阻尼损耗最小化的LCL滤波器参优化设计［J］.中国电机工程学报，2010，30（27）：90-94.Wang Yaoqiang，Wu Fengjiang.Optimized design of LCL filter for minimal damping loss［J］.Proceedings of the CSEE，2010，30（27）：90-94.

［8］王盼，刘飞.基于有源阻尼的并联有源滤波器输出LCL滤波器设计［J］.电力自动化设备，2013，33（4）：161-166.Wang Pan，Liu Fei.Design of output LCL filter based on shunt APF with active damping［J］.Electric Power Automation Equipment，2013，33（4）：161-166.

［9］刘虔，彭力.一种基于图解的LCL滤波器设计和优化方法［J］.中国电机工程学报，2012，32（36）：36-42.Liu Qian，Peng Li.A design and optimization method of LCL filters based on the graphic-analysis［J］.Proceedings of the CSEE，2012，32（36）：36-42.

［10］许津铭，谢少军.LCL滤波并网逆变器的鲁棒电流控制［J］.电力系统自动化，2012，19（36）：99-103.Xu Jinming，Xie Shaojun.A robust current control strategy for grid-connected inverters with LCL filters［J］.Au-tomation of Electric Power Systems，2012，19（36）：99-103.

［11］雷一，赵争鸣.LCL滤波的光伏并网逆变器有源阻尼与无源阻尼混合控制［J］.电力自动化设备，2012，11（32）：23-27.Lei Yi，Zhao Zhengming.Hybrid control of active and passive damping for grid-connected PV inverter with LCL filter［J］.Electric Power Automation Equipment，2012，11（32）：23-27.

［12］Agorreta，Borrega，López.Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants［J］.IEEE Transactions on Power Electronics，2011，3（26）：770-785.

［13］Dannehl，Fuchs.Limitations of voltage oriented PI current control of grid-connected PWM rectifiers with LCL filters［J］.IEEE Transactions on Industrial Electronics，2009，2（56）：380-388.

［14］He Ning，Xu Dehong.Weighted average current control in a three phase grid inverter with a LCL Filter［J］.IEEE Trans actiens on Industrial Electron ics，2013，28（6）：2085-2098.

［15］沈国桥，徐德鸿.LCL型并网逆变器的分裂电容法电流控制［J］.中国电机工程学报，2008，28（18）：36-41.Shen Guoqiao，Xu Dehong.Current control for grid-connected inverters by splitting the capacitor of LCL filter［J］.Proceedings of the CSEE，2008，28（18）：36-41.

Optimization Design of Output LCL Filter for Inverter Connected-Grid

YANG Gongde1，SHI Huoquan1，WU Lei1，WANG Meng2
（1.School of Internet of Things Engineering，Jiangnan University，Wuxi 214122，China；2.School of Automation，Guangdong University of Technology，Guangzhou，510006，China）

The LCL filter owned superior filter performance，integrated and encapsulated easily，is becoming more and more widely used in the distributed generation system connected-grid.However the resonance occurred by zero damping not only affects the stability of the closed-loop system，but also decreases the performance of net current.So how to design and optimize the filter parameters to improve the filter performance of the filter becomes the hot spot of the research.Under the conditions of the total inductance and the capacitance can meet the filter performances，the paper analyzes comparatively how the inductance distribution coefficient and damping resistance impact on the stability of the system，filtering effect，switch order harmonic attenuation ratio，damping value and the damping loss.On this basis，proposed an optimization method，and given the general design flow chart.The simulation results show the optimization method is effective.

LCL filter；inductance distribution coefficient；damping resistance；filtering effect；damping loss