基于SVPWM的七相感应电机谐波消除方法研究

2015-01-03骆海燕黎梅云郭冀岭

电源学报 2015年1期

关键词：基波定子矢量

骆海燕，陆可，黎梅云，郭冀岭

（西南交通大学电气工程学院，成都 610031）

基于SVPWM的七相感应电机谐波消除方法研究

骆海燕，陆可，黎梅云，郭冀岭

（西南交通大学电气工程学院，成都 610031）

在电压源逆变器供电的多相电机驱动系统中，由于电机在广义零序子空间中的阻抗很小，采用传统SVPWM将会导致较大的定子谐波电流。在分析七相感应电机数学模型和逆变器基础上，针对3次、5次空间谐波问题，提出了一种基于SVPWM的谐波消除方法。通过调节矢量作用的顺序，同时使3次、5次子空间合成矢量为零来消除3次、5次谐波电流。在Matlab/Simulink仿真软件和七相感应电机调速平台下，通过仿真和实验验证了所提出控制算法的正确性和有效性。

七相感应电机；空间矢量脉宽调制；谐波消除；谐波子空间

引言

与传统的三相感应电机相比，七相感应电机有很多突出的优点：降低对功率器件容量的要求，易于实现低压大功率调速；同时由于相数冗余，运行可靠性高，转矩脉动小［1］。文献［2-3］选择两个电压矢量合成SVPWM，其目的是为了减少开关次数从而减少开关损耗。但只是传统三相SVPWM的简单推广，没有考虑电压矢量在广义零序子空间中的影响；文献［4］针对七相电压型逆变器提出的SVPWM引入了电压矢量作用占空比的概念，简化了计算，但对谐波问题考虑较少。

本文在详细分析七相感应电机数学模型及其电压源逆变器空间矢量的基础上，提出一种低输出谐波和低开关损耗的控制方法［5］。根据空间解耦思想，电压矢量在基波子空间作用的同时，其投影在谐波子空间内也会产生合成矢量，用3种幅值、6个矢量来合成参考矢量［6］，并通过调整矢量施加顺序及时间，同时使3次、5次谐波子空间合成矢量为零，以达到消除谐波的效果。

1 七相感应电机数学模型

对于七相感应电动机的建模和控制应该从七维空间的角度考虑［7］。因此，选择适当的空间变换，可以使得控制任务得到简化，多相感应电动机的解耦变换矩阵公式［8］为

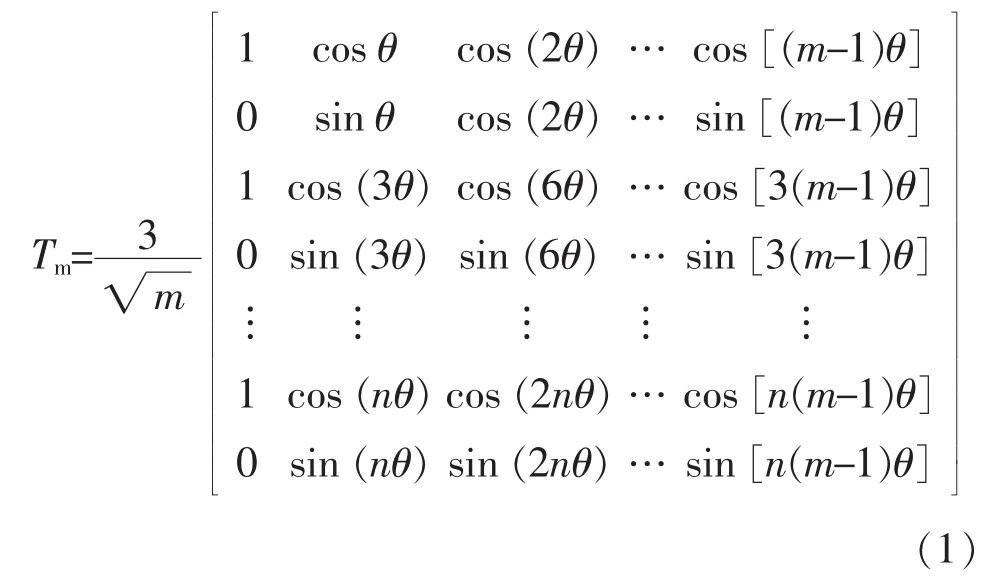
式中：m为多相感应电动机的相数；n＝2［m/2］±1（m为奇数时取“＋”，m为偶数时取“-”），［m/2］是取整运算，且当m为奇数时矩阵中无最后一行。因此，利用多相感应电动机的变换公式可得出七相感应电动机的解耦变换矩阵T7。θ＝2π/7时，T7为

矩阵前两行对应基波子空间（α-β），电机变量中基波和14k±1（k＝0，1，2，...）次谐波都被映射到该子空间上，形成旋转磁场，参与机电能量转换；第3行和第4行、第5行和第6行分别对应3次谐波子空间（z11-z12）和 5次谐波子空间（z21-z22），14k±3次谐波和14k±5次谐波被分别映射到这两个子空间上，不产生旋转磁场，但会产生谐波电流；矩阵的最后一行对应零序子空间，7k次谐波被映射到该子空间上（定子7相Y接可忽略该空间）。

利用旋转变换，将转子侧的变量变换至定子侧，从而得到七相感应电动机的数学方程。由于电机的定子绕组开路并不影响转子侧结构，故转子侧的变换矩阵仍然为T7［9］。

将该变换阵代入到自然坐标系下电机方程，可得旋转坐标系下基波子空间电压、磁链和转矩方程分别为

式中：Ψs、Ψr分别为定、转子磁链基波；Ls、Lr分别为定、转子自感；Lm为互感；Rs为定子电阻；Rr为转子电阻；ωs、ωsl分别为定子频同步角速度和转差；np为极对数；p为微分算子。

2 七相逆变器的空间电压矢量分析

七相感应电机电压逆变器如图1所示。

图1 七相感应电机逆变器系统结构Fig.1 Structure of seven-phase induction motor inverter

七相逆变器有128个电压矢量，0、127为零矢量，非零矢量中除去35、75、70…101和69、39、23…83两组矢量外，剩余7组矢量形成同心正14边形，平面可以被细分为十四个扇区，每个扇区的夹角度数为π/7［10-11］。电压矢量分布如图2所示。

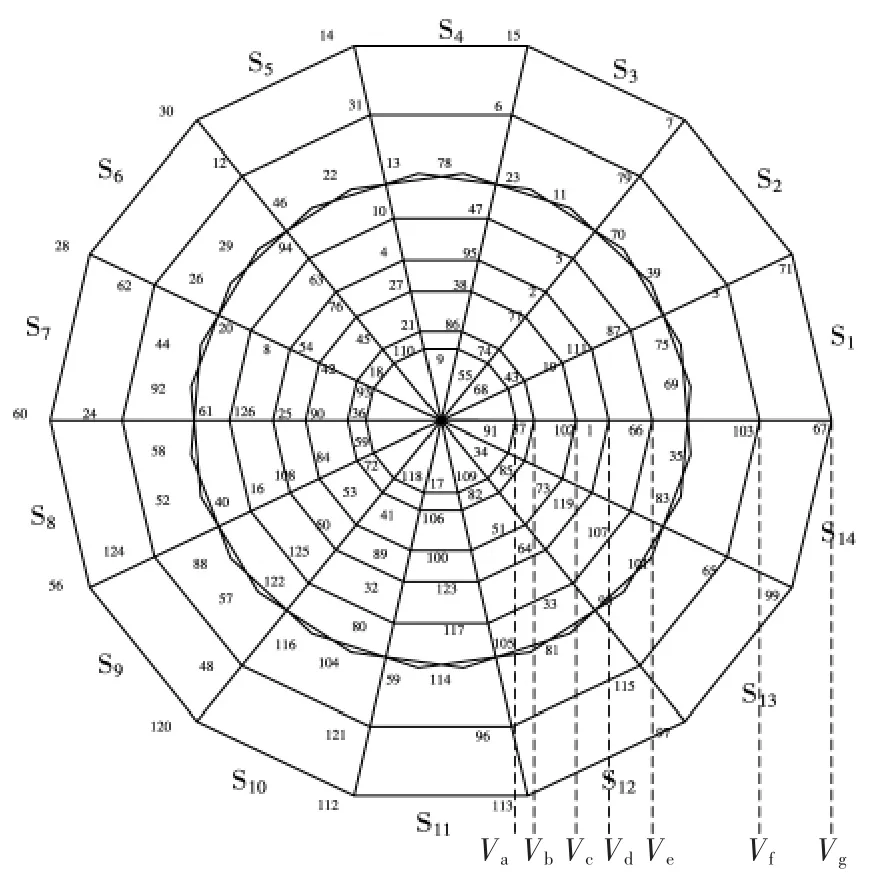
图2 七相系统电压矢量分布Fig.2 Distribution of seven-phase system voltage vector

图中的每一个电压矢量相对应的二进制数代表了逆变器的开关状态［12］，从低位到高位依次为abcdefg。令最小圈矢量幅值为Va，最大圈矢量幅值为Vg，以此类推，矢量幅值从小到大分别为Va、Vb、Vc、Vd、Ve、Vf、Vg。通过数学验算可得各个电压矢量幅值之间的数学关系［13］为

2014年至2017年，全省扶持的微型企业带动社会投资分别为28.04亿元、84.88亿元、94.27亿元、40.33亿元，4年累计带动社会投资247.51亿元，已成为拉动全省民间投资增长的新生力量。从申报企业行业分类来看，全省零售业、农业、租赁和商务服务业、养殖业、餐饮业、软件和信息技术服务业、批发业、工业、信息传输业等重点行业微型企业占比达92%。涌现了一批以高原特色农业、现代特色服务业为代表的特色产业板块，微型企业行业多元化、产业特色化趋势逐步显现。

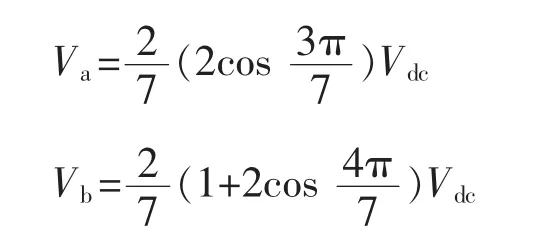
则各矢量幅值之比为：Va∶Vb∶Vc∶Vd∶Ve∶Vf＝0.127∶0.159∶0.229∶0.286∶0.356∶0.515∶0.642。

本文提出的SVPWM基本思想是从多维矢量空间调制的观点出发，以负载等效电路为基础找出电压矢量之间的关系，运用集合的方法对其进行了分类，选择其中具有代表性的电压矢量集合来实现PWM算法。

电压型逆变器中开关状态决定了负载等效电路的结构［14］。例如对于一个七相电压逆变器，开关状态为（1110000）时，其负载等效电路为4个负载并联再与另外3个并联负载串联，定义｛C34｝为等效电路，所以一个七相电压逆变器有3种基本的负载等效电路：｛C16｝、｛C34｝和｛C25｝。

相应地，七相逆变器有｛C16｝、｛C25｝和｛C34｝3个电压矢量集合。每一个集合根据其开关状态中“1”的相邻性可继续分为若干个子集，例如在｛C25｝中，开关状态（1100000）和（01100000）中“1”都是连续的，它们有相同的“1”的相邻性，对应的电压矢量属于相同的子集；而开关状态（1110000）和（1100100）则不具有相同的“1”的相邻性，对应的电压矢量属于不同的子集［15］。

Vd组的14个矢量构成｛C16｝；Vf、Va、Ve这三组矢量虽然属于｛C25｝组合，但是Va、Ve中开关状态的“0”或“1”不具备相邻性，属于伪｛C25｝组合，应避免使用；同理，Vg组矢量属于｛C34｝组合，Vb、Vc组属于伪｛C34｝组合。

选定｛C16｝、｛C25｝和｛C34｝3个集合中基波子空间组Vd、Vf、Vg构成的电压矢量来实现，使合成的电压矢量最大，对电机来说，则会使形成的定子磁通更大。具体实现方法如下。

选定Vd、Vf、Vg三组电压矢量，以基波空间第一扇区S1为例，分别投影在两谐波子空间中，见图3。

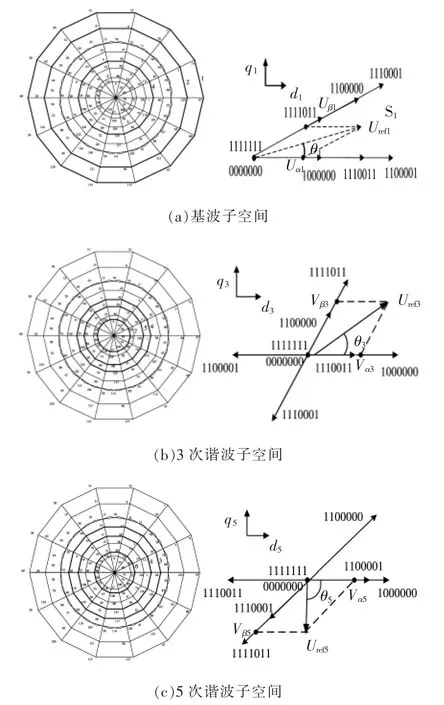
图3 七相系统空间矢量3个子空间Fig.3 Three voltage vector subspaces of seven-phase system

3 七相SVPWM谐波消除算法原理

在基波子空间施加电压矢量合成参考矢量的同时，在谐波子空间也会分别产生3次和5次谐波合成矢量。为消除3次、5次谐波，需要使3次谐波子空间和5次谐波子空间合成均为0。由图3可得

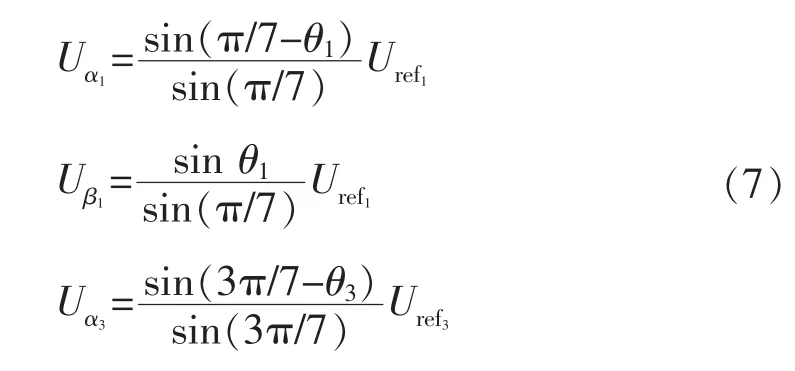
在基波子空间，以扇区S1为例，开关周期Ts内除去零矢量作用时间，有效矢量按Vd1（1）-Vf2（3）-Vg1（67）-Vg2（71）-Vf1（103）-Vd2（111）顺序，会获得较少的开关次数和较小的开关损耗。作用时间分别为T1、T2、T3、T4、T5、T6。由伏秒平衡关系可知：

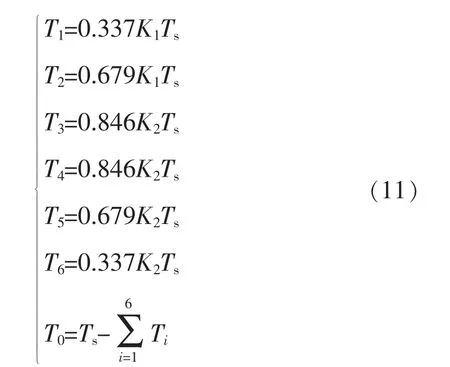
其中：

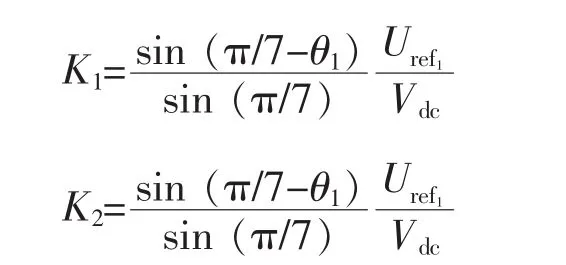
由此SVPWM算法中各相桥臂开关动作电平变化如图4所示。

图4 SVPWM在扇区S1内矢量作用时间及相互转换Fig.4 Function time and conversion in sector S1of SVPWM

4 仿真结果与实验验证

七相感应电机参数如下：定子电阻为0.631 Ω，转子电阻为1.123 Ω，定子电感为22.57 mH，转子电感为22.57 mH，互感为21.6 mH，转动惯量为0.144 kg·m2，极对数为2，仿真中给定转速为980 r/ min，在t＝0.8 s时，突加20 N·m负载，直流电压Ud为200 V，转矩限幅值为20 N·m，开关频率设置为5 kHz。仿真结果如图5所示。

图5（a）、图5（b）为电机转速与电磁转矩，在0.8 s突加负载时，转速经过0.01 s后便能稳定在980 r/min左右，转矩有轻微的脉动；图5（c）为传统SVPWM调制方法的负载相电流ia，存在很大的3次和5次定子谐波电流；图5（d）为使用本文提出方法的负载相电流ia，电流基本为正弦波形状；图5（e）为消谐前负载相电压Ua；图5（f）为消谐后负载相电压Ua。仿真结果表明谐波得到有效消除。

利用TI公司的TMS320F28335数字信号处理芯片作为本文实验平台的主要控制芯片。实验结果波形如图6、图7所示。以七相感应电机b相为例，采用本文方法后，消谐前后对比，显然，定子电压Ub、电流ib谐波大大减少，谐波得到有效抑制。

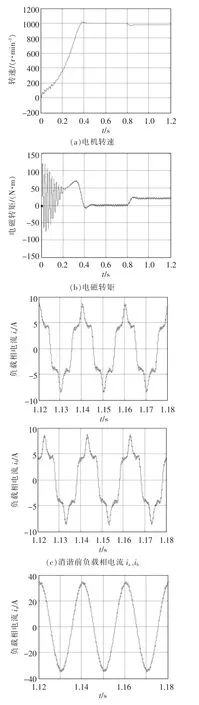
图5 仿真波形Fig.5 Simulation waves

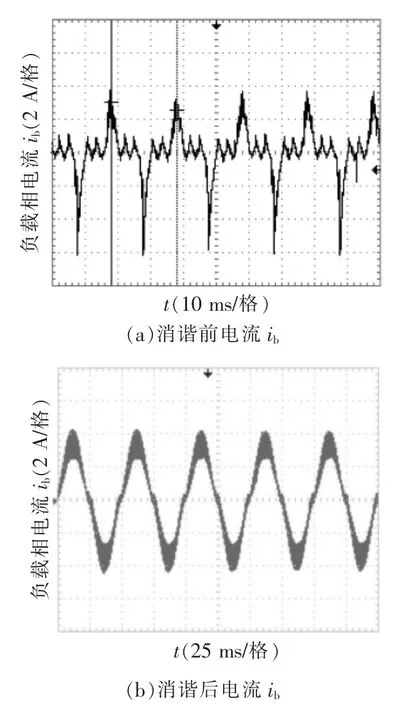
图6 负载相电流ib波形Fig.6 Simulation waves of load phase current

图7 相电压仿真波形Fig.7 Simulation waves of phase voltage

5 结语

针对七相感应电机传统SVPWM调制时3、5次谐波子空间定子电流谐波大的问题，结合基于DSP28335的实验平台，提出一种可行的消除子空间谐波理论，并提供了具体实现方法。通过仿真分析和实验，该方法不仅在d-q子空间中合成的给定电压矢量满足转矩控制的要求，而且使3、5次子空间中合成电压矢量为零，有效抑制了电流谐波，减少了开关次数，同时又获得了对转矩和转速的良好动态控制，实验结果表明本文所提出的控制算法的正确性和有效性。

［1］Levi E，Bojoi R，Profumo R，et al.Multiphase induction motor drives-a technology status review［J］.IET Electric，Power Application，2007，1（4）：489-516.

［2］Yu Fei，Zhang Xiaofeng，Li Huaishu，et al.The space vector PWM control research of a multi-phase permanent magnet synchronous motor for electrical propulsion［J］.ICEMS，2003，2：604-607.

［3］Shi Ruhe，Toliyat H A.Vector control of five-phase synchronous reluctance motor with space pulse width modulation for minimum switching losses［J］.IAS2001，2001，3：2097-2103.

［4］Casadei D，Dujic D，Levi E，et al.General modulation strategy for seven-phase inverters with independent control of multiple voltage space vectors［J］.IEEE Transactions on Industry Electronics，2008，55（5）：1921-1932.

［5］宋庆国，张晓锋，等.高性能五相逆变器PWM算法研究［J］.电力电子技术，2007，11：106-109.Song Qingguo，Zhang Xiaofeng，et al.Research on high performance PWM technique of Five-Phase inverter［J］.Power Electronics，2007，11：106-109（in Chinese）.

［6］Kelly J，Strangas E.Multiphase space vector pulse width modulation［J］.IEEE Transactions on Energy Conversion，2003，18（2）：259-264.

［7］薛山，温旭辉.一种新颖的多相 SVPWM［J］.电工技术学报，2006，21（2）：68-72，107.Xue Shan，Wen Xuhui.Nover multiphase SVPWM［J］.Transactions of China Electrotechnical Society，2006，21（2）：68-72，107（in Chinese）.

［8］李山.多相感应电机控制系统的研究［D］.重庆大学，2009.Li Shan.Research on the Control Technologies of Multiphase Induction Machine［D］.Chongqing：School of Electrical Engineering，Chongqing University，，2009（in Chinese）.

［9］郭冀岭，肖建，等.基于 DSP28335的七相感应电机矢量控制［J］.电源学报，2014，12（1）：74-83.Guo Jiling，Xiao Jian.Vector control of Seven-Phase induction motor based on DSP28335［J］.Journal of Power Supply，2014，12（1）：74-83（in Chinese）.

［10］Grandi G，Serra G，Tani A.Space vector modulation of a seven-phase voltage source inverter［J］.ICEMS，2006，8：6-11.

［11］Casadei D，Mengoni M，Serra G，et al.Seven-phase Induction Motor Drive Based on Stator Flux Vector Control［C］.Power Electronics Electrical Drives Automation and Motion（SPEEDAM）.Pisa，Italy，2010：1628-1633.

［12］Dong Tian，Lin Chen，et al.Modeling an Simulation of Dural Three-phase Induction Machine with Two Opened Phases［C］.International Conference on Digital Object Identifier，2008.

［13］Domenico Casadei，Drazen Dujic，Emil Levi，et al.General modulation strategy for seven-phase inverters with independent control of multiple voltage space vectors［J］.IEEE Transactions on Industry Electronics，2008，55（5）：1921-1932.

［14］Amin A H，Wooi H P，Arof H，et al.Fuzzy logic control of a three phase induction motor using field oriented control method［C］.Proceedings of the 41st SICE Annual Conference.New York，IEEE，2002：264-267.

［15］侯立军.多相感应电机变频调速系统的研究［D］.西安：西安交通大学，2003.Hou Lijun.Multi-phase Induction Machine Drive Research［D］.Xi’an：School of Electrical Engineering，Xi’an Jiaotong University，2003（in Chinese）.

Research of Harmonic Elimination Method for Seven-phase Induction Motor Based on SVPWM

LUO Haiyan，LU Ke，LI Meiyun，GUO Jiling
（College of Electric Power Engineering，Southwest Jiaotong University，Chengdu 610031，China）

In the multiphase motor drive system supported by VSI，the traditional SVPWM will lead to larger stator harmonic current，due to the small impedance in the generalized zero sequence subspaces.According to the 3rd and 5th harmonics problem in seven-phase VSI and mathematical model，this paper proposes a novel SVPWM method.By adjusting the vector sequence，it can make the synthetic vector be zero in the 3rd and 5th sub space，and reduce the 3rd and 5th harmonic component.Finally，using Matlab/Simulink and the seven-phase IM test bench，the simulation and experimentation results prove the validity and effectiveness of the proposed method.

seven-phase induction motor；SVPWM；harmonic elimination；harmonic sub-space