参考作物蒸腾量的多重分形特性分析

张 杰,刘国栋,孙怀卫,吴 静

（1.重庆水利电力职业技术学院水利工程系,重庆 402160；2.中国科学院南京土壤研究所土壤与农业可持续发展国家重点实验室,南京 210008；3.华中科技大学水电与数字化工程学院,武汉 430074）

参考作物蒸腾量的多重分形特性分析

张 杰1,刘国栋2,3,孙怀卫2,3,吴 静3

（1.重庆水利电力职业技术学院水利工程系,重庆 402160；2.中国科学院南京土壤研究所土壤与农业可持续发展国家重点实验室,南京 210008；3.华中科技大学水电与数字化工程学院,武汉 430074）

分析ET（Evapotranspiration,参考作物蒸腾量）的动力学特性,有助于进行中长期需水量的分析与预测。将多重分形特性分析方法应用于1978—2007年间30 a汉江流域3个典型站点（钟祥、天门、武汉）的参考作物ET时间序列。结果表明,逐日参考作物ET序列不仅具有不规则的高频振荡的特征,而且还具有明显的分形行为；在不同时间宽度（日、旬、月）下,逐日参考作物ET序列的多重分形特征最强。进一步的分析结果表明,序列中脉动引起的波动相关性和极端事件引起的胖尾概率等都是引起多重分形特征形成的原因。结合趋势转折分析方法发现：不同时间阶段内的多重分形特征显著；但在不同的时间段内,多重分形谱和局部分维宽度等都受到了极端事件的影响,且影响幅度与所处流域内的位置有关。

水资源；参考作物蒸腾量；年代转际；多重分形分析；趋势转折分析方法

2015,32（12）：18－24,35

1 研究背景

作物需水量是进行水文循环分析和水资源评价过程中的一个重要参数[1－2］。参考作物ET的计算是分析实际需水量的基础,由此引发了对作物需水过程及其变化机理、预报及模拟等相关研究的广泛关注[3－4］。

气候系统的变量序列中往往存在着不同尺度间的自相似性结构[5］,应用混沌和分形的方法对气候变量的非线性演化过程进行定量分析发现,气候系统在大尺度上存在高低值的振荡,而不同峰谷区间内又存在更小尺度的高低值振荡,即其变化呈现出不同时间宽度、不同尺度间的自相似分形结构[6］。一般认为,作物需水量受作物自身生理机制以及近地层气象因子非线性、非平稳变化的影响也具有自相似的特点。刘丙军等[7］用单分形结构分析了参考作物ET的分形特征；谢先红等[4］采用多重分形非趋势波动分析法分析了参考作物ET时间序列的长程相关性和分形特性。

分形理论解释了复杂系统中有序与无序、确定性与随机性的统一,通过分形维数可以定量描述系统变量的自相似结构特征[8］。在一些复杂系统中,不同的局部条件可能导致不同的局部特性,针对事物的测量单位可能导致对系统的整体认识有很大不同[9］,因此单分形可能无法全面描述非均匀的多分形结构。多重分形,又称为多重分形测度,能刻画包括气候系统在内的多种非均匀性特征,多种研究方法（包括MFDFA、配分函数法等）的应用也逐渐趋于多样化[10］。本文利用多重分形的配分函数法,通过计算汉江流域典型站点1978—2007年间30 a的参考作物ET,深入研究其多重分形特性,并结合年代转际分析方法,分析影响需水量变化的动力学机理,为参考作物ET的研究提供实证基础。

2 资料和方法

2.1 研究区域

南水北调中线工程可能引起流域内不同区域供水和需水的不确定性,并由此引起了研究者的广泛关注[11］。汉江流域的整体地势为西北高、东南低,上游山岭高度海拔一般在1 000 m以上,下游泛滥平原地带的海拔多在50 m以下；对流域内高程（DEM）数据统计分析表明,其地势分布中海拔50 m以下的平原占流域总面积的9.9%,50～250 m的低缓岗地占27%。由此可见汉江流域地势起伏不平,可能造成流域内的水文水情存在很大的差异。针对汉江流域特性,为分析参考作物ET时间序列特性,选择位于汉江流域中下游的典型站点,从上游到下游依次为钟祥、天门和武汉站,3个站点的平均海拔高度为41.0 m,能够较好地反映下游平原的海拔高度。通过搜集气象站点的逐日气温和降水数据,结合由中国气象局国家气象中心气象资料室提供的观测资料,经过对数据的完整性、一致性和极值检验,选取了30 a（1978年1月1日至2007年12月31日）的逐日数据。表1给出了典型站点的基本信息和气象特征,研究区域及气象站点分布见图1。其中,钟祥站平均风速较大,而武汉站平均气压和平均气温较大,3个典型站点之间的平均ET位于2.26～2.36 mm之间。

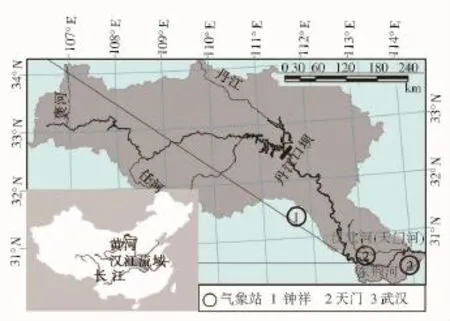
图1 汉江流域及气象站位置Fig.1 Layout of different meteorologic stations in the Hanjiang basin of China

2.2 参考作物ET序列的计算模型

在土壤水充足、作物生育状况正常的状况下,农田消耗于作物蒸腾和棵间土壤蒸发的总水量称为作物需水量。作物需水量反映了作物对水分的需求,目前常用的计算方法是先计算参考作物ET,再经过不同作物需水系数的修正得到实际作物需水量。而计算参考作物ET的模型较多,目前广泛应用的是FAO推出的Penman-Monteith模型。由于1998年的Penman-Monteith模型具有物理机制清晰,适应于不同气候区和推广应用较广等特点,在我国应用最多,且经过了较多学者进行的方法应用比较研究[12］,因此本文选用此模型进行参考作物ET的计算。

2.3 趋势分析方法

趋势分析方法主要用于对气候系统内的不同时间范围所对应的阶段性变化特征进行描述,能够识别叠加在更长期变化趋势的扰动。气候系统内的突变一般可以归为均值突变、变率突变和趋势突变3类。其中：均值突变是指一个气候的基本状态（以平均值表示）向另一个气候的急剧变化；变率突变是指变率变化中的2个气候状态的平均值并无明显差异,但其变率有极明显的不同；趋势突变则主要是因为2个气候阶段具有完全相反的变化趋势。变化趋势转折判别模型（piecewise linear fitting model,PLFIM）是最近提出的一种新方法,所利用的数学原理参见文献[13］。计算准则如下：①趋势转折点之间的间隔必须等于或者超过某一给定的值；②两个连续分段的线性趋势变化必须遵从趋势符号相反（趋势突变）或趋势变化达到某种程度（变率突变）的原则；③根据计算结果得到的最佳分段组合,得到所需时间尺度上的趋势转折点检验结果以及各时间段的线性变化趋势。

2.4 多重分形分析方法

参考作物ET作为一种气候序列,内在的大振幅脉动与小振幅脉动间可能存在不同的长程相关性,有可能会导致内在多分形标度行为[5］。多重分形分析能够分析分形维的混合状态,更加真实地描述系统的复杂统计特性,弥补了传统统计分析模型的不足,是刻画气候变化复杂波动的有力工具[4］。方法主要是将复杂体系分成许多奇异度不同的区域,通过具有时变性的参数来刻画气候数据时间序列的局部特征。配分函数（partition function）法是多重分形分析的一种,并被用在金融时间序列、水文河流分区、降雨序列和土壤水的分析中[10,14－15］。

针对参考作物ET时间序列特性,多重分形分析方法还可以结合一些数据变换方法进一步地对多重分形行为的原因进行分析。通常时间序列中的多重分形行为存在2种原因：①小幅波动和大幅波动中不同的长程相关性会造成多重分形；对数据进行重排处理,可以保持波动分布但破坏了相关性,从而可以用来辨识多重分形是否由此引起。②波动的胖尾概率分布引起多重分形。因此,对数据进行相位随机化替代处理可以弱化时间序列分布的非高斯性。重排和替代处理的步骤见文献[16］。

表1 典型站点信息及气象特征Table 1 Basic information and meteorologic characteristics of typical sites

本文采用配分函数（partition function）法对参考作物ET的时间序列进行多重分形分析,具体数学原理如下：由参考作物ET计算变化序列（如日、旬或月）为,其中T为序列的长度。将该测度μ的支撑集分为尺度为l的盒子,可得N＝T/l个盒子,第n个盒子内的测度为

于是,q阶配分函数xq（l）为

式中,q的取值范围为－∞到∞间的整数,可视实际情况而定。不同的q表示不同等份在配分函数中的作用不同,从而将分形体分成具有不同层次的区域来进行研究。根据参考作物ET时间序列的长度,本文q的取值范围假定为－50≤q≤50。在计算过程中,当时,为了避免数值计算中内存消耗过大,可用式（3）等价计算配分函数xq（l）的对数。

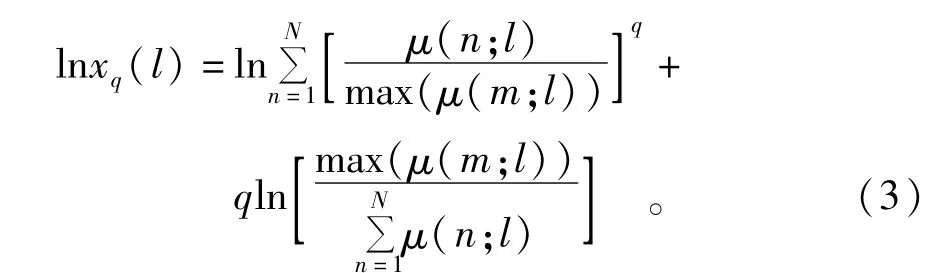
若测度μ具有自相似性,则标度指数函数τ（q）存在；通过求取lnxq（l）～lnl的斜率能够得到τ（q）。且若τ（q）为q的线性函数,则测度μ为单分形；若τ（q）为q的非线性函数（或凸函数）,则μ为多重分形。

对标度指数函数τ（q）进行勒让德变换后,可以得到如下关系成立：

式中：α（q）称为局部分维,又称为奇异性指数,反映了所对应的区域发生的几率；f（α）称为标度指数,又称为多重分形奇异谱。利用数值计算可以得到奇异谱f（α）随奇异性指数α（q）的变化曲线,称为多重分形谱曲线（f（α）-a曲线）,反映了概率分布的特征。

3 多重分形及成因分析

3.1 多重分形分析

在依据Penman-Monteith模型计算出的参考作物ET的基础上,为分析变量的多尺度振荡特征和不同时间尺度的层次结构,需要根据选取的不同时间尺度计算平均值作为时段内循环值。通过观察变量的距平序列,可以了解时间序列的不同尺度振荡特性和标度行为。逐日参考作物ET去掉年循环后的变动序列如图2所示。去掉参考作物ET的年循环后,序列中仍然包含了剧烈变化及快速涨落等多尺度的高频振荡特征；同时序列的不规则振荡也反映了不同尺度的振荡间可能存在不同的标度及分形行为。作物需水量受气温、辐射、风速等气象因素的影响,以前有学者研究也表明,平均气温等变量表现出了多重分形的特征,且这种分形特征与长程记忆性更为相关[5］。因此,图2中所呈现的小振幅脉动和大振幅脉动共存的现象,虽然可能说明了参考作物ET序列可能存在多重分形特征,但是仍需要进一步地量化分析。

图2 不同站点的参考作物ET时间序列Fig.2 Time series of reference crop evapotranspiration in different stations

为了定量分析参考作物ET的多重分形特征,对不同时间标度下的lnxq（l）-lnl曲线进行了分析,如图3所示。图中的5条线所代表的阶数q从上到下依次为－50,－20,0,20,50,从结果可知,当q＜0时,具有微小的抖动,但整个尺度范围内呈现线性关系；当q≥0时,在整个尺度变化范围内都呈现了良好的线性关系,由此可以看出参考作物ET的时间序列在规定的尺度内具有明显的分形特征。图3中也可以看到,在以日、旬、月为时间宽度下计算得到的双对数曲线都较为接近,而且在q＜0时的线性关系较为一致,也验证了ET序列的分形特性；在以日为时间标度下的分形标度不变性达到了5个数量级（超过10 000个数据,即约30 a数据）。由此验证了本研究中所选取的数据长度较为合适,对于参考作物ET的研究中需要注意研究数据长度的选取,多重分形特征与长程记忆性之间的关系分析需要依赖长序列的研究数据。

图3 不同时间标度下的lnxq（l）-lnl曲线Fig.3 Curves of lnxq（l）vs.lnl in different time scales

图4中给出了不同时间标度下的标度指数τ（q）和q之间的关系。从图4中可以看出,以日为时间宽度下得到的曲线关系为非线性曲线关系,体现了逐日作物ET序列的多重分形特性。而以旬、月为时间宽度的τ（q）-q曲线呈近似线性关系,表明作物ET多重分形不明显。逐日作物ET序列所存在的多重分形特征说明,可以用分形理论来解释逐日作物ET序列的变化,这对于分析作物ET波动动力学的机理研究非常重要。为了分析作物ET序列所存在的多重分形特性,尤其是识别逐日作物ET序列的多重分形成因,因此有必要开展多重分形成因分析。

图4 不同时间标度下的τ（q）-q曲线Fig.4 Curves of τ（q）vs.q in different time scales

3.2 多重分形成因分析

经过对作物ET的原始、替代和重排处理,能够通过对作物ET序列的τ（q）-q曲线的分析进而得到多重分形特征的成因。从图5中可以看出,经过变换的逐日作物ET序列的多重分形强度中,3种处理的多重分形特征的强度依次为替代＞原始＞重排,由此可以说明对于作物ET序列变动中的持久相关性起了一定的作用,但相对而言,胖尾概率（极端事件）的影响可能造成ET序列的较大变化。因此,参考作物ET受胖尾概率影响较大,说明对于参考作物ET的分析中需要注重对于极端事件的分析,结合图2的结果,更加可以说明长时间的参考作物ET序列研究中极端事件的影响不可忽略。冯涛等[5］（2010）对北京地区的气候变量进行随机重排处理后发现,气候序列的内在多分形标度行为是由大振幅脉动与小振幅脉动间不同的长程相关性引起的；但从以上分析可以发现,重排后的逐日ET序列的多重分形特征依旧比较明显,说明序列的波动相关性和胖尾分布都会导致多重分形特征。

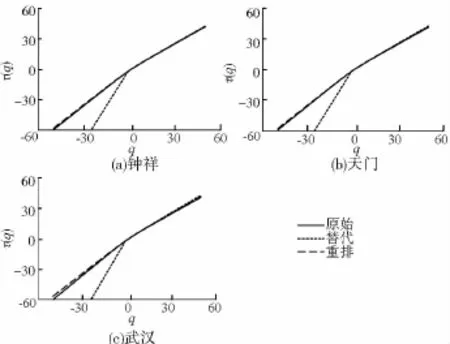
图5 逐日作物ET序列的τ（q）-q曲线Fig.5 Curves of τ（q）vs.q of daily evapotranspiration series

图6给出了逐日时间序列的多重分形谱f（α）-α曲线。从结果中可以看出,替代序列的多重分形谱明显宽于原始序列,这说明参考作物ET的时间序列具有明显的自身特性,替代数据序列破坏了参考作物ET的规律性特征；重排序列的多重分形谱宽度比原始序列略窄,这说明ET序列经过重排处理后的多重分形随之减弱,证明参考作物ET波动的变化存在一定的持久相关性。以上的分析中,揭示了需水量的多重分形性质可能既由系统内的自组织行为造成,同时也可能由于时间范围内的某些极端事件引起。

图6 逐日ET序列的f（α）-α曲线Fig.6 Curves of f（α）vs.α of daily evapotranspiration series

在已有其他地点开展的研究中发现,对ET随机重排处理后的多重分形性质不明显[4］。在气候系统的研究中,人们也发现对于一个时间尺度较长的气候序列,整个时间段上的线性趋势可能并不能描述出气候变化的波动特征[13］。为此,需结合针对整段时间范围内的年代际趋势转折分析工具,对不同时间范围内的分形特征进行分析。

4 年代际多重分形特征变化

根据年代际转折分析（PLFIM）方法[13］,对参考作物ET的年均值进行了计算和判别,结果如图7所示。图7中还给出了30 a趋势的参考作物ET的变化趋势,3个典型站点的ET变化趋势都为略微减小趋势,但年代际变化显著。其中：对于钟祥站点,1978—1985年间ET呈减小趋势,1986—1999年间ET略微增加,2000—2007年间ET显著增加；对于天门站点,1978—1985年间ET呈减小趋势,1986—1998年间ET显著增加,1999—2007年间ET显著减小；对于武汉站点,1978—1991年间ET有减小趋势,1992—1999年间ET略微增加,2000—2007年间ET显著增加。由此可以发现,对于汉江流域内的典型站点,1985年、1991年、1998年、1999年均为年代际转折发生的关键节点；参见各典型站点的水利志可以发现,天门地区1984年末、钟祥地区1985年遭受了旱灾,而1991年、1998年均存在流域内的洪灾,由此可见年代际转折的分析结果与历史性的极端事件发生较为一致。

图7 1978—2007年均参考作物ET的变化趋势Fig.7 Trend of annually-mean crop reference evaportranspiration in 1978—2007

为了考察不同时间范围对ET序列的多重分形谱的影响,按照年代际转折分析结果,分别对3个典型站点的不同年代际阶段的参考作物ET序列进行分析。不同年代际的逐日时间序列τ（q）-q曲线如图8所示。从图中可以看出,3个阶段内的标度指数函数τ（q）与q之间的关系都呈现出非线性的趋势,即具有明显的多重分形特征。其中,最早一个阶段内（钟祥、天门为1978—1985年；武汉为1978—1991年）的非线性趋势在3个站点中都比较明显,多重分形特征最强。

图8 不同年代际的逐日时间序列τ（q）-q曲线Fig.8 Curves of τ（q）vs.q of daily series in different periods

不同年代际的逐日ET序列的多重分形f（α）和局部维α的相互关系曲线如图9所示。从图中可以看出,不同时间范围内的多重分形谱曲线的高度和宽度存在较大的差异,其中第1阶段（钟祥、天门为1978—1985年；武汉为1978—1991年）的多重分形宽度都相对较大,表明了这一时期的ET序列的多重分形特性较强；而第2阶段（钟祥为1986—1999年；天门为1986—1998年；武汉为1992—1999年）的多重分形宽度相对较小,表明这一时期的ET序列受极端事件影响较大,多重分形特性较弱。其中,位于汉江流域中游的钟祥、天门站点,在第2阶段的f（α）＜1,这说明ET序列变化的不确定性增加；由此可以说明,极端事件对于河流中上游地区的影响要大于下游。

图9 不同年代际的逐日时间序列f（α）-α曲线Fig.9 Curves of f（α）vs.α of daily series in different periods

根据不同年代范围内的ET序列的多重分形谱计算结果,3个典型站点的局部分维α和多重分形谱f（a）变化范围如表2所示。从表中可以看出,3个站点内的局部分维宽度Δα变化幅度为0.120～0.485,多重分形谱高差Δf（α）为0.611～0.973。其中,第2阶段内的局部分维宽度Δα平均变化幅度较小,仅为0.203,所对应的Δf（α）为0.718；第一阶段的变化幅度最大；这说明第1个时间范围内的ET序列的多重分形特征最强,而最近的多重分形特征减弱,这一结果也与近来我们所感知的极端事件频率增加等较为相符。在站点的相互比较上,武汉站点的局部分维宽度Δα要大于钟祥和天门站点,但多重分形谱变化幅度Δf（α）没有明显的增加,造成这个现象的原因可能是下游地区影响ET的极端事件发生概率较大。

表2 不同年代范围内参考作物ET的多重分形谱参数Table 2 Multifractal spectrum parameters of reference crop evapotranspiration in different periods

5 结 论

本文通过多重分形的配分函数法和变化趋势转折判别模型（PLFIM）法相结合,定量分析了汉江流域3个典型站点（钟祥、天门和武汉）参考作物ET序列的多重分形结构,很好地描述了多分形结构特征和不同年限范围内的分形变化规律。得到了如下结论：

（1）通过分析逐日参考作物ET去掉年循环后的变化序列,发现序列具有不规则高频振荡的特征,反映了作物需水量序列的不同标度及分形行为；结合进一步的统计矩函数和尺度的关系曲线,可以发现在不同尺度下参考作物ET分形特性,但标度指数函数的分析揭示逐日ET的多重分形特征最强。这对于分析需水量的波动动力学机理研究具有重要意义。

（2）为了分析参考作物ET的多分形行为,通过对原始序列进行重排和替代处理,通过多重分形谱的差异表征了ET序列中脉动引起的波动相关性和极端事件（胖尾概率）等可能对需水量造成的影响,为分析气候变化条件下的需水量预测等建立了理论基础。

（3）结合趋势转折分析结果,对不同时间范围内的ET序列的多重分形特征进行分析,结果发现,不同时间阶段内的多重分形特征都十分明显；但在不同的时间段内,多重分形谱和局部分维宽度等都受到了极端事件的影响,且影响幅度可能与所处流域内的位置有关。由此,可以根据不同的地区特点和需水量变化特征,合理构建区域的水资源配置体系,加强风险管理。

参考文献：

[1]陈 燕.江苏省长江流域片水资源配置模型及应用[J］.水力发电学报,2011,30（4）：79－84.（CHEN Yan.Model of Water Resources Allocation and Its Application to Jiangsu Yangtze River Basin[J］.Journal of Hydroelectric Engineering,2011,30（4）：79－84.（in Chinese））

[2]金菊良,洪天求,王文圣.基于熵和FAHP的水资源可持续利用模糊综合评价模型[J］.水力发电学报,2007,26（4）：22－28.（JIN Ju-liang,HONG Tian-qiu,WANG Wen-sheng.Entropy and FAHP Based Fuzzy Comprehensive Evaluation Model of Water Resources Sustaining Utilization[J］.Journal of Hydroelectric Engineering,2007,26（4）：22－28.（in Chinese））

[3]王晓红,侯浩波.有作物的潜水蒸发规律试验研究和理论分析（1）——有作物生长条件下的潜水蒸发规律试验研究[J］.水力发电学报,2008,27（4）：60－66.（WANG Xiao-hong,HOU Hao-bo.Study on Shallow Groundwater Evaporation Laws of Crops and Bare Soil[J］.Journal of Hydroelectric Engineering,2008,27（4）：60－66.（in Chinese））

[4]谢先红,崔远来,周玉桃.参考作物蒸腾量时间序列的长程相关性和多重分形分布[J］.水利学报,2008,39（12）：1327－1333.（XIE Xian-hong,CUI Yuan-lai,ZHOU Yu-tao.Long-term Correlation and Multi-fractality of Time Series of Reference Crop Evapotranspiration[J］.Journal of Hydraulic Engineering,2008,39（12）：1327－1333.（in Chinese））

[5]冯 涛,付遵涛,毛江玉.北京地区气候变化的多分形特征研究[J］.地球物理学报,2010,53（9）：2037－2044.（FENG Tao,FU Zun-tao,MAO Jiang-yu.The Multi－fractal Characteristics of Climate Variables in Beijing[J］.Chinese Journal of Geophysics,2010,53（9）：2037－2044.（in Chinese））

[6]FENG Tao,FU Zun-tao,DENG Xing,et al.A Brief Description to Different Multi-fractal Behavior of Daily Wind Speed Records over China[J］.Physics Letters A,2009,373：4134－4141.

[7]刘丙军,邵东国,沈新平.参考作物蒸腾量时间分形特征研究[J］.灌溉排水学报,2006,25（5）：9－13.（LIU Bing-jun,SHAO Dong-guo,SHEN Xin-ping.Research on Temporal Fractal Features of Reference evapotranspiration[J］.Journal of Irrigation and Drainage,2006,25（5）：9－13.（in Chinese））

[8]GHASHGHAIE S,BREYMANN W,PEINKE J,et al.Turbulent Cascades in Foreign Exchange Markets[J］.Nature,1996,381（6585）：767－770.

[9]都国雄,宁宣熙.上海证券市场的多重分形特性分析[J］.系统工程理论与实践,2007,（10）：40－47.（DU Guo-xiong,NING Xuan-xi.Mutifractal Analysis on Shanghai Stock Market[J］.Systems Engineering：Theory＆Practice,2007,（10）：40－47.（in Chinese））

[10］LOPES R,BETROUNI N.Fractal and Multifractal Analysis：A Review[J］.Medical Image Analysis,2009,13（4）：634－649.

[11］康 玲,何小聪,熊其玲.基于贝叶斯网络理论的南水北调中线工程水源区与受水区降水丰枯遭遇风险分析[J］.水利学报,2010,41（8）：908－913.（KANG Ling,HE Xiao-cong,XIONG Qi-ling.Risk Analysis for Precipitation Rich-poor Encounter between Source Area and Receiving Area of the Middle Route of South-to-North Water Transfer Project Based on Bayes-net theory[J］.Journal of Hydraulic Engineering,2010,41（8）：908－913.（in Chinese））

[12］彭世彰,徐俊增.参考作物蒸发蒸腾量计算方法的应用比较[J］.灌溉排水学报,2004,23（6）：5－9.（PENG Shi-zhang,XU Jun-zeng.Comparison of Computing Methods of Reference Crop Evapotranspiration[J］.Journal of Irrigation and Drainage,2004,23（6）：5－9.（in Chinese））

[13］TOMÉ A R,MIRANDA P M A.Piecewise Linear Fitting and Trend Changing Points of Climate Parameters[J］.Geophysical Research Letters,2004,31（2）：L02207.

[14］MASCARO G,VIVONI E R,DEIDDA R.Downscaling Soil Moisture in the Southern Great Plains through a Calibrated Multifractal Model for Land Surface Modeling Applications[J］.Water Resource Research,2010,46（8）：863－863.

[15］VENUGOPAL V,ROUX S G,FOUFOULA-GEORGIOU E,et al.Revisiting Multifractality of High-resolution Temporal Rainfall Using A Wavelet-based Formalism[J］.Water Resource Research,2006,42（6）：376－389.

[16］苑 莹,庄新田.国际汇率的多重分形消除趋势波动分析[J］.管理科学,2007,20（4）：80－85.（YUAN Ying,ZHUANG Xin-tian.Multifractal Detrended Fluctuation Analysis of International Exchange Rates[J］.Journal of Management Sciences,2007,20（4）：80－85.（in Chinese））

（编辑：刘运飞）

Multifractal Analysis of Time Series of Reference Crop Evapotranspiration7

ZHANG Jie1,LIU Guo-dong2,3,SUN Huai-wei2,3,WU Jing3
（1.School of Hydraulic Engineering,Chongqing Water Resources and Electric Engineering College,Chongqing 402160,China；2.State Key Laboratory of Soil and Sustainable Agriculture,Institute of Soil Science of Chinese Academy of Sciences,Nanjing 210008,China；3.School of Hydropower and Information Engineering,Huazhong University of Science and Technology,Wuhan 430074,China）

In order to predict water requirement in the medium-to-long period,we studied dynamics features of reference crop evapotranspiration.Multifractal analysis was applied to the time series of reference crop evapotranspiration of three stations（Zhongxiang,Tianmen and Wuhan）,located in Hanjiang basin from 1978 to 2007.Results show that,the daily reference crop evapotranspiration contains characteristics of irregular high-frequency fluctuation and exhibits the strongest multifractal characteristics among different time intervals such as one day,ten days and one month.Further analysis by partition function shows that,most part of multifractality in the time series’data was due to correlations caused by fluctuations and the fat-tailed probability distributions caused by extreme events.Moreover,the multifractal features vary within the different parts of the time series and the changes can be explained by the methods of piecewise linear fitting and trend changing points（PLFIM）.Finally,both of multifractal spetrum and local piecewise width are influenced by extreme climate events in different time intervals,and the effects of extreme climate events are relevant to different locations in basin.

water resources；reference crop evapotranspiration；inter-decadal variation；multifractal analysis PLFIM；

S161.4；TV213

A

1001－5485（2015）12－0018－07

10.11988/ckyyb.20140550

2014－07－04；

2014－09－01

国家自然科学基金项目（51309106,51239004）；华中科技大学自主创新基金项目（2014QN235）

张 杰（1983－）,男,重庆人,讲师,主要研究方向为水资源评价,（电话）13996192362（电子信箱）zhmuxin＠foxmail.com。

孙怀卫（1985－）,男,湖北天门人,讲师,博士,主要研究方向为水文学及水资源,（电话）13419600578（电子信箱）huaiweisun＠whu.edu.cn。