埋深对地下结构地震反应特点的影响研究

岳粹洲，郑永来

(同济大学土木工程学院,上海 200092)

埋深对地下结构地震反应特点的影响研究

岳粹洲，郑永来

(同济大学土木工程学院,上海 200092)

在地震作用下,地下结构的地震响应影响因素复杂多变,地下结构的埋深就是其中之一。针对地下结构埋深对地下结构的地震动响应的影响,通过建立处于不同埋置深度的2种结构模型,运用FLAC软件进行数值模拟研究。研究表明,在地震作用下,同一位置的地震波,在保持入射波不变的情况下,当地下结构位于不同的埋置深度时,结构上相同位置的地震响应差别不明显。

埋深；地下结构；地震响应；异同性；FLAC软件

2015,32(11):78-81

1 研究背景

近年来,为了拓展城市空间,地下空间的发展日益受到重视。与大量的地面结构震害相比,地下结构震害资料相对较少,导致一段时间以来,人们普遍认为地下结构具有较好的抗震性能,未对地下结构抗震研究给予足够重视。在地下结构设计时,设计人员往往只是盲目地照搬地面结构的抗震设计方法。但是近些年来,特别是1995年日本阪神地震以后,由于阪神地震中大量的地下结构和地下设施遭到严重破坏,地下结构抗震问题受到了研究人员的关注,成为近些年地震工程领域的研究热点[1-2]。

地下结构的抗震设计不像地面结构那样,拥有完善的抗震设计规范和方法。近年来,经过众多学者的努力,虽然提出了许多地下结构抗震设计方法,但是各种方法基本上都是针对特定结构或土体性质提出的,适用性有限,至今还没有一种普遍适用于地下结构的抗震设计方法[3]。现有的地下结构抗震研究方法主要可分为3个大的类别:原型观测、理论分析和模型试验。模型试验方法是地下结构抗震研究的一个重要途径,主要包括人工震源试验、振动台试验和离心机振动台试验。振动台试验开展相对较多,近年来取得丰硕的成果。徐志英、施善云[4](1993)采用加重乳胶铁粉材料制作成方形管道模型,在3 m×5 m的大型振动台上进行试验,采用简谐波在垂直于结构轴线的水平方向激振,测定了地下结构内的动应力以及砂土与地下结构接触面上的动土压力及加速度,在实验基础上提出了土-地下结构动力相互作用的计算模型。杨林德等[5](2003)对典型地铁车站结构、地铁车站接头结构进行了大型振动台试验(台面尺寸4.0 m×4.0 m,最大承载15 t),通过试验获得了模型加速度时程、结构构件应变和结构表面动土压力等数据,进一步了解了软土中地铁结构动力反应的规律,并为改进计算模型和分析方法进而制定软土条件下地铁抗震设计指南等提供了依据。陶连金等[6](2006)对地铁车站结构进行了振动台模型试验,采用多次加载方式,得到了不同荷载级别下的中柱及侧墙钢筋,中柱、顶板及侧墙混凝土的应变反应,结构模型及周围土层的加速度时程以及土与结构之间的接触压力反应等。然而,上述所有的试验均是针对特定的结构或者有固定的设定参数,但是如果改变其中的埋深参数,试验结果是否仍然有效有待商榷,本文将针对埋深对地下结构的地震响应影响进行研究。

2 数值模拟

2.1 模型描述

笔者为了探索地下埋深对结构抗震性能的影响,考虑到结构一般纵向较长,故而对其一断面进行二维平面特性分析,借助于二维有限差分软件FLAC,拟对一单层结构针对其不同位置采用FLAC软件进行模拟分析。针对某一地区,取长20 m、高10 m的区块,进行网格划分,网格单元边长为1 m,取为正四边形网格。该地下结构为单层单跨结构,净跨为3 m,净高为3 m,柱截面宽为0.24 m,梁截面高0.24 m,基础梁截面高为0.3 m。为了比较二者的振动特点,建立了2种不同埋深的结构位置模型,埋深分别为地面以下2 m和地面以下5 m(即结构顶部距地面的距离),相应位置见图1。模型中土体的边界条件根据实际情况设置为:底部边界x方向和y方向均固定,左右两侧边界的x方向固定。

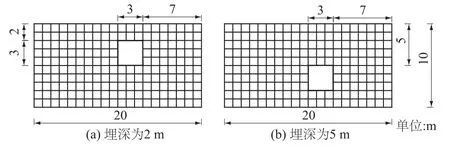
图1 结构在地面以下所处位置示意图Fig.1 Layout of the structures under the ground

2.2 材料模型及参数

2.2.1 土体模型

土体材料采用FLAC软件中提供的应变软化本构模型,它的黏聚力可以起到弱化土壤材料塑形应变的作用。这种模型与拉力流动法则相关联,在塑性屈服开始后,内聚力、摩擦角、剪胀扩容和抗拉强度可能会发生变化,试验中将内聚力定义成分段线性函数。应变软化本构模型基于Mohr-Coulomb本构模型发展而来[7],其屈服条件的一般形式为

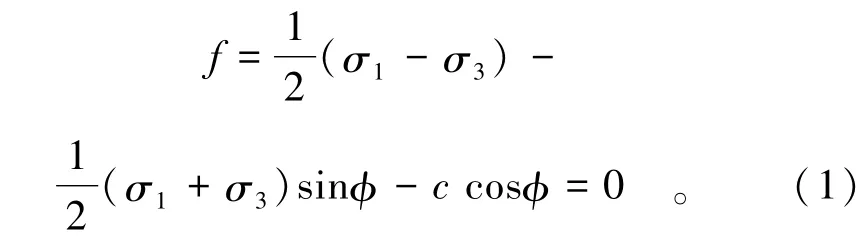
式中:σ1,σ3分别为平面内最大、最小主应力；φ为材料的内摩擦角；c为材料的凝聚强度。

在Mohr-Coulomb模型中,内摩擦角φ和凝聚强度c在材料的整个受力屈服过程中均保持不变,而在应变软化本构模型中可能会遵循某一函数形式进行变化,实验中将内聚力c定义为分段线性函数[8-9]。土壤材料性质具体参数见表1、表2及图2。

2.2.2 结构模型

研究中所分析的结构,采用FLAC软件中的结构单元进行模拟,主要采用梁结构单元,梁结构单元有2组不同的参数取值,其中结构模型中的梁、柱采用材料编号为2的梁结构单元进行模拟,基础梁采用材料编号为1的梁结构单元进行模拟,具体参数取值见表3。

表1 土壤材料性质Table 1 Properties of the soil

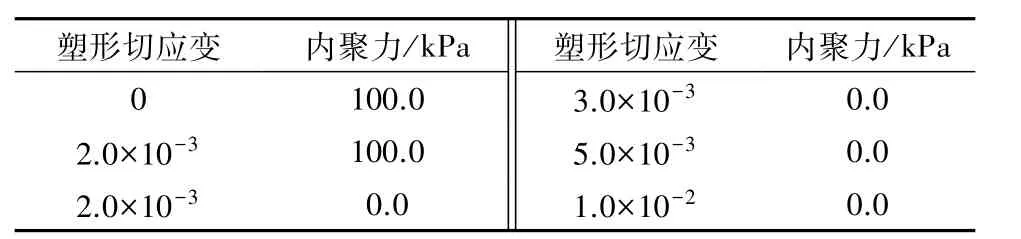
表2 土壤材料的塑形切应变与内聚力的对应关系Table 2 Corresponding relation between plastic shear strain and cohesion of the soil

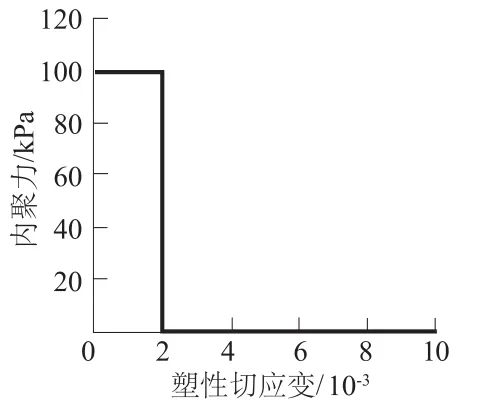
图2 土壤材料的塑形切应变与内聚力的对应关系取值Fig.2 Relation between plastic shear strain and cohesion of the soil

表3 梁结构单元的材料特性Table 3 Material properties of the beam structural element

2.2.3 模型校核

该模型试验中动力荷载的加载过程是,在模型的底部施加x方向的正弦波。正弦波的振幅为1 m/s,频率为10 Hz,入射波方程为

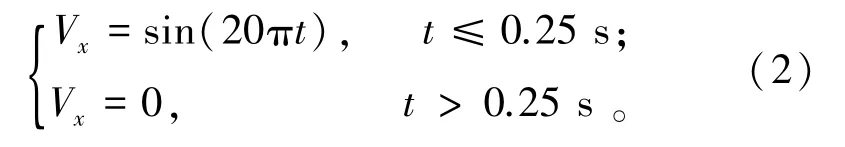
基于材料的弹性性质,压缩波和剪切波的波速[10]可以按下式进行计算:

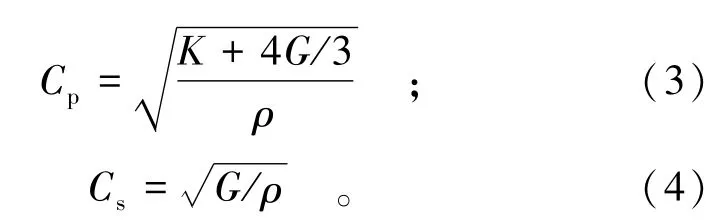
式中:Cp为压缩波波速；Cs为剪切波波速；K为材料的体积模量；G为材料的剪切模量；ρ为材料密度。

根据式(3)和式(4)可以计算得到压缩波和剪切波波速分别为Cp=840 m/s和Cs=485 m/s。建模过程中模型网格划分的最大单元尺寸为1 m,可以计算出此网格能够传递的波的最小频率。体系振动时,体系第一振型时的基本频率f的计算公式为

式中:C为与振型对应的波速；λ为与振型对应的最大波长。

Kuhlemeyer和Lysmer[11](1973)提出,为了能够更清晰地反应波在模型中的传递,模型单元的空间尺寸Δl必须小于输入波中最小频率所对应波长的1/10～1/8,即

式中λ为输入波成分中具有不可忽略的能量成份的最小频率所对应的波长。

根据式(5)和式(6)可以计算得出该模型模拟的波最小频率为

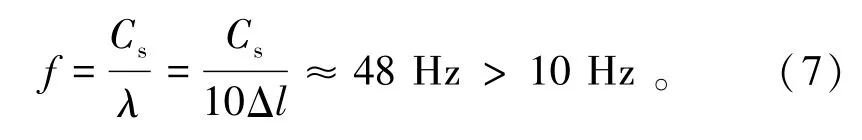
因此,该模型的单元尺寸足够小,能够满足输入频率波的传递。

此外,该试验的本构模型采用应变软化模型,该模型中的塑形流动特性能够消散波传递中的大部分能量,因此对于振动试验的结果分析来说,振动阻尼的选择就不是必要的,本试验采用无阻尼的形式。在输入动力过程中,采用振幅为1 m/s、频率为10 Hz的正弦波,持续时间为0.25 s。模型左侧和右侧的边界条件设为自由场边界,用于吸收波的能量,减少反射波。

2.3 数值模拟结果

在模型底部输入前面已经介绍的正弦波,主要检测结构顶部右侧的端点位置节点(建模时属于结构节点编号为7,将上部结构的节点7位置记为节点7,将下部结构的节点7位置记为节点7′)的时程曲线,然后进行不同情况下的比较,本文主要检测了节点的水平方向的速度曲线和位移曲线,然后进行对比分析。

对于节点的水平方向位移响应,见图3(a),图中分别给出了上部与下部结构上相同节点7位置处在地震波输入时间段0.5 s内的水平位移响应曲线,实线表示的是上部结构节点7的水平位移响应,虚线表示的是下部结构节点7′的水平位移响应；对于节点的水平方向速度响应,见图3(b),图中给出了节点7位置处在地震波输入时间段0.5 s内的节点水平速度响应曲线,实线表示的是上部结构节点7处的水平速度响应,虚线表示的是下部结构节点7′处的水平速度响应。

从图3(a)中可以看出,上部结构节点7处的水平方向最大位移略低于0.04 m,下部结构节点7处的水平方向最大位移略高于0.04 m,二者相差很小,基本可以忽略。其它各时刻,上、下部结构节点7处的水平位移也基本相当。从而可以得出结论:对于结构上的同一位置点处,当结构埋深不同时,其在振动作用下的水平方向位移响应的区别不大,基本相同。

从图3(b)中可以看出,在水平振动波作用下,在与输入波方向一致的方向上,上、下部结构上节点7处的水平响应速度基本相同；而在与输入波反向的方向上,节点7处的水平响应速度最大值略有差别,尤其是在动力荷载作用输入的前0.25 s时间内,反方向的最大速度有最大不超过0.1 m/s的差别,在动力输入结束后,正反方向的速度基本一致,并且周期也一致。从而可以得出结论:对于结构上的同一位置点处,当结构埋深不同时,其在振动作用下的水平方向速度响应的区别同样不大,基本相同；从速度的响应曲线上同样可以得到,位于不同位置的节点7的加速度响应也基本一致。

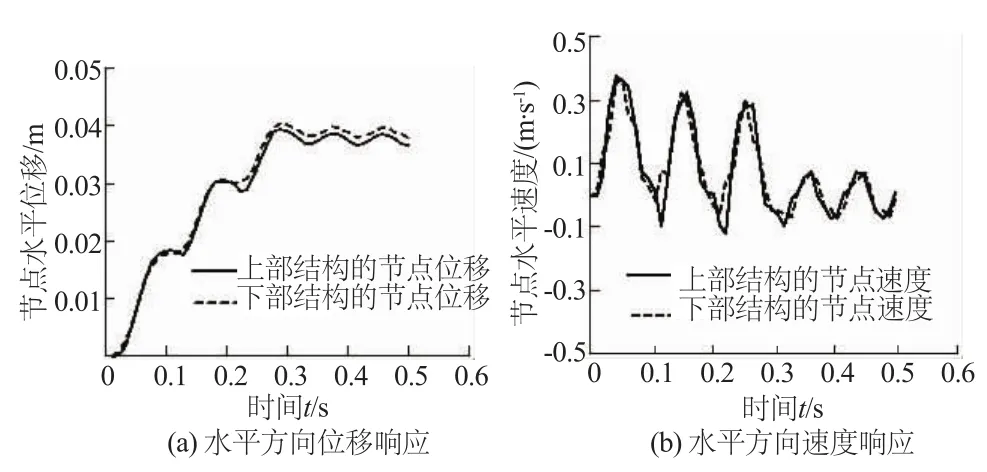
图3 节点7的水平方向位移和速度响应Fig.3 Responses of the horizontal displacement vs. time and horizontal velocity vs.time at point 7

3 结 论

以上的研究表明,在地震作用下,对于同一位置的地震波,入射方向相同,且波形不变的情况下,当地下结构位于不同的埋置深度时,结构上相同位置的地震响应差别不明显,可以认为基本相同。因此,在进行地震作用下地下构筑物或建筑物的振动台地震模拟时,模型结构的埋深对于试验结果的影响基本可以忽略,在考虑地震影响的各种复杂因素时可以不考虑埋置深度的影响,简化试验研究的复杂程度。

[1]孙 超,薄景山,齐文浩,等.地下结构抗震研究现状及展望[J].世界地震工程,2009,25(2):94-99.(SUNChao,BO Jing-shan,QI Wen-hao,et al.Status and Prospect of Seismic Research on Underground Structures[J].World Information on Earthquake Engineering, 2009,25(2):94-99.(in Chinese))

[2]郑永来,杨林德,李文艺,等.地下结构抗震[M].上海:同济大学出版社,2011.(ZHENG Yong-lai,YANG Linde,LI Wen-yi,et al.Underground Structure Seismic[M].Shanghai:Tongji University Press,2011.(in Chinese))

[3]白广斌,赵 杰,汪 宇.地下结构抗震分析方法综述[J].防灾减灾学报,2012,28(1):20-26.(BAI Guang-bin,ZHAO Jie,WANG Yu.Review of Methods for Antiseismic Research of Underground Engineering[J].Journal of Disaster Prevention and Reduction, 2012,28(1):20-26.(in Chinese))

[4]徐志英,施善云.土与地下结构动力相互作用的大型振动台试验与计算[J].岩土工程学报,1993,15(4):1-7. (XU Zhi-ying,SHI Shan-yun.Large-scale Shaking Table Model Test and Calculation on the Dynamic Interaction Between Soil and Underground Structure[J].Chinese Journal of Geotechnical Engineering,1993,15(4):1-7. (in Chinese))

[5]杨林德,季倩倩,郑永来,等.软土地铁车站结构的振动台模型试验[J].现代隧道技术,2003,40(1):7-11. (YANG Lin-de,JI Qian-qian,ZHENG Yong-lai,et al. Shaking Table Model Test on the Underground Structure of Subway Station in Soft Soil[J].Modern Tunnelling Technology,2003,40(1):7-11.(in Chinese))

[6]陶连金,王沛霖,边 金.典型地铁车站结构振动台模型试验[J].地震工程与工程振动,2008,28(1):157-164.(TAO Lian-jin,WANG Pei-lin,BIAN Jin.Shaking Table Model Test on Typical Subway Station Structure[J].Earthquake Engineering and Engineering Vibration, 2008,28(1):157-164.(in Chinese))

[7]夏志皋.塑性力学[M].上海:同济大学出版社,2008. (XIA Zhi-gao.Plastic Mechanics[M].Shanghai:Tongji University Press,2008.(in Chinese))

[8]Itasca Consulting Group,Inc.FLAC(Fast Lagrangian A-nalysis of Continua)Online Manual[K].Minnesota, USA:Itasca Consulting Group,Inc.,2001.

[9]刘 波,韩彦辉.FLAC原理、实例与应用指南[M].北京:人民交通出版社,2005.(LIU Bo,HAN Yan-hui. Theories,Examples and Applications of FLAC[M].Beijing:China Communications Press,2005.(in Chinese))

[10]JOYNER W B,CHEN A T F.Calculation of Nonlinear Ground Response in Earthquakes[J].Bulletin of the Seismological Society of America,1975,65(5):1315-1336.

[11]KUHLEMEYER R L,LYSMER J.Finite Element Method Accuracy for Wave Propagation Problems[J].Journal of the Soil Mechanics and Foundations Division,1973, 99(5):421-427.

(编辑:姜小兰)

Research of the Influence of Embedded Depth on Seismic Response of Underground Structure

YUE Cui-zhou,ZHENG Yong-lai
(School of Civil Engineering,Tongji University,Shanghai 200092,China)

Under the seismic action,factors affecting the seismic response of underground structure are complicated,among which the embedded depth of underground structures is taken into consideration.In order to know effects of embedded depth on seismic response of structures,we established two models with different depths,using the FLAC software for numerical simulation.The research result shows that,for given position of seismic wave,responses for underground structures at different embedded depths tend to be not obviously different under the conditions of unchanged incident wave.

embedded depth；underground structure；seismic response；difference and similarity；FLAC software

TU93

A

1001-5485(2015)11-0078-04

10.11988/ckyyb.20140459

2014-06-05；

2014-07-03

岳粹洲(1988-),男,安徽颍上人,硕士研究生,从事地下结构抗震方面的研究,(电话)021-65981565(电子信箱)ycz_hao@sina. com。