地下岩体裂隙蠕变渗流耦合分析

陈俊国，刘卫群，梁浩楠

(1.中国矿业大学力学与建筑工程学院,江苏徐州 221008；2.山东科技大学矿业与安全工程学院,山东青岛 266590)

地下岩体裂隙蠕变渗流耦合分析

陈俊国1，2，刘卫群1，梁浩楠1

(1.中国矿业大学力学与建筑工程学院,江苏徐州 221008；2.山东科技大学矿业与安全工程学院,山东青岛 266590)

震后断层区岩体裂隙的愈合对于地震水力响应研究具有重要的作用。为研究裂隙岩体愈合对深部断层区渗透率时空演化规律的影响,在离散裂隙网络藕合模型基础上加入裂隙蠕变效应,建立裂隙岩体流固藕合时空演化模型,并利用COMSOL Multiphysics对建立的藕合方程进行求解。结果表明:封堵之前,常规的藕合渗流达到稳定状态,由于具有完整的通道,任意时刻的流固藕合并不能改变流体的压力；随着封堵发生,在蠕变效应下,裂隙开度减小,单元体渗透率降低,流体压力增大。该研究成果为震后破裂带岩体的愈合机理及渗透率演化分析提供了理论依据。

裂隙岩体；蠕变效应；渗透率；裂隙开度；流固藕合

2015,32(11):45-51

1 研究背景

由裂隙主导的地下岩体损伤区水力特性对于地震的产生和传播具有重要的影响[1-3]。地下流体不仅参与地震孕育发生的全过程,而且充当地震信息传播的媒介。美国劳伦斯伯克利国家实验室的Montgomery和Manga[4]详细探讨了溪流量和井水水位对地震的响应,认为由地震引起的地壳变形以及地表振荡通过固结地表沉积物、岩石裂隙扩展、含水层变形以及裂隙中充填物的阻塞与清除来影响地下裂隙岩体的渗透率,并且通过观察认为溪流量和井水水位的变化幅度与地震震级有密切的关系；Wang (2003)[5]根据1999年台湾井水对集集地震的响应情况提出了井水水位的4种响应形式,认为影响地震水力响应的因素是繁多复杂的；Wang等(2008)[6]通过观察发现,震后井水水位随时间表现出较大范围的波动；Liu等[7-8]在实验室中研究了裂隙砂岩在动态载荷下渗透率变化的规律,并且在裂隙中添加充填物研究振动对裂隙含沙渗流的的影响；Geballe等[9]利用汶川地震过后台湾刘家井的水位变化数据,提出了新的模型解释渗透率随时间的指数型递减规律,与Brodsky等[10]提出的模型进行对比分析,显示了较好的结果；Elkhoury等[11]应用井水水位对地球固体潮的响应测量地层渗透率,通过对20 a期间地震过后渗透率的测量,认为地震波能够增加地层的渗透率,并认为此发现为提高煤层气及石油的开采效率提供了一种可能的方法；Xue等[3]在汶川震后地层破裂区应用深部钻孔实时监测地下水位潮汐响应的方法测量渗透率随时间的变化,在大部分情况下,当断层区岩体愈合时,渗透率将会迅速下降,并且揭示了大地震过后,在远震影响下断层区岩体愈合和破裂交替进行的过程。

以往研究[9-10]均是根据实地测量结果和经验给定渗透率模型,此类模型主要是从宏观角度对现象进行解释,并不能从微观机理及各个影响因素层面进行定量分析,而地层渗透率的变化是由固体岩石的力学环境和流体流动相互作用的复杂过程。本文基于前人的现场监测和实验室测试结论,综合考虑应力环境和流体流动特性,将裂隙岩体愈合能力归因于裂隙的蠕变效应,建立考虑蠕变效应的裂隙网络岩体藕合渗流模型,探讨震后破裂区裂隙岩体渗透率的时空演化规律。

2 岩体裂隙蠕变模型

裂隙岩体的蠕变特性一直是岩石力学研究的重要内容,目前对完整岩石和裂隙面蠕变模型的研究成果[12-14]较多。杨松林等[13]在Huang[15]给出的单一裂隙面的弹性本构关系基础上将变形增量、柔度矩阵和应力增量表示为时间的函数,给出了单一裂隙面的蠕变关系,即

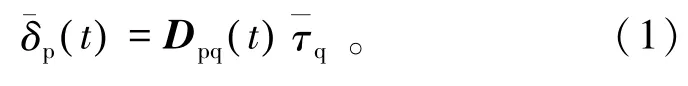
或者

为了简化裂隙蠕变模型,杨松林等[13]忽略裂隙面法向应力作用下的蠕变变形,将法向变形视为固定的弹性变形。实际上,当裂隙面较软弱、法向力较大时,裂隙面的法向蠕变变形会比较明显。因此,将法向刚度和切向刚度表示为时间的函数,并代入式(2)得:

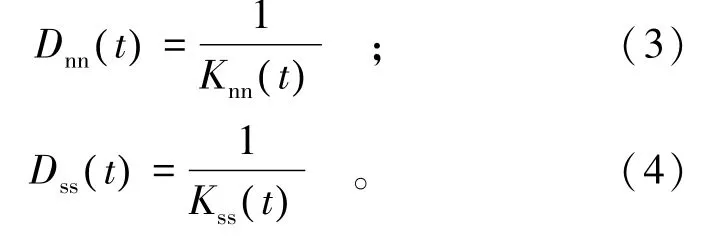
若裂隙面的法向和切向蠕变变形规律均符合广义Kelvin模型,则有

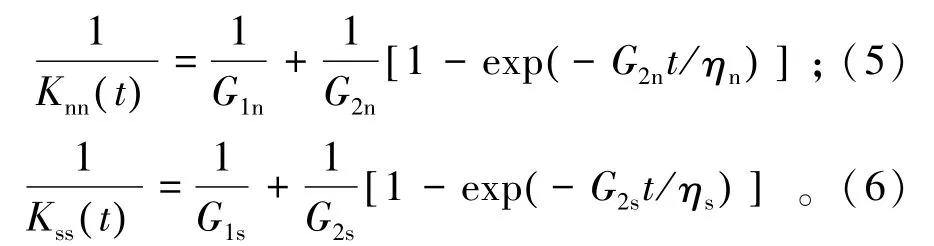
式中:G1n,G2n和ηn分别为裂隙面的法向弹性模量、黏弹性模量和黏滞系数；G1s,G2s和ηs分别为裂隙面的切向弹性模量、黏弹性模量和黏滞系数。

本文建立的裂隙蠕变-渗流模型中,裂隙体积模量只与法向刚度有关,忽略剪胀效应,表征单元体内裂隙的变化只与裂隙和岩块的体积模量有关。因此,本文采用裂隙面法向蠕变的广义Kelvin模型作为裂隙蠕变的基本模型,探讨裂隙岩体地层渗透率的时空演化规律。设裂隙的法向刚度为Kn,则有

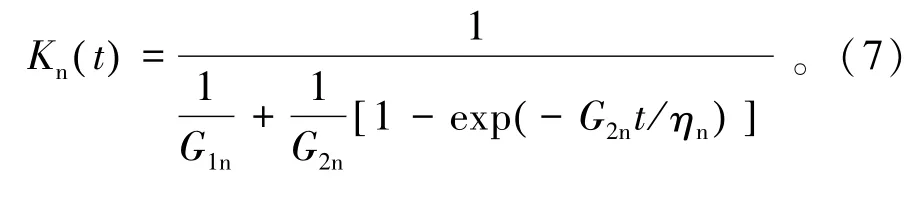
3 裂隙蠕变-渗流耦合模型

本文基于双重孔隙介质模型[16]建立裂隙蠕变-渗流藕合模型,模型中,REV表征单元体由岩块和裂隙组成,断裂区由裂隙主导,忽略岩块的渗透率,水流在裂隙中进行。模型中综合考虑了外在应力和流体压力共同作用下岩块的变形、裂隙的变形、裂隙的蠕变效应及裂隙-流体的藕合过程。模型推导基于以下假设:

(1)震后断裂区裂隙密布,裂隙是流体流动的主要通道,忽略岩块的渗透率。

(2)流体流动符合达西渗流法则。

(3)裂隙区充满流体,即饱和渗流。

(4)蠕变只发生在裂隙面之间,忽略岩块的蠕变。

3.1 裂隙网络岩体变形的控制方程

根据假设,如图1所示,岩体被概化为具有相同尺寸的岩块和裂隙的结构[16]。岩块为长度为a的立方体块,岩块之间为裂隙,宽度为b,σ为作用于岩体的外力。

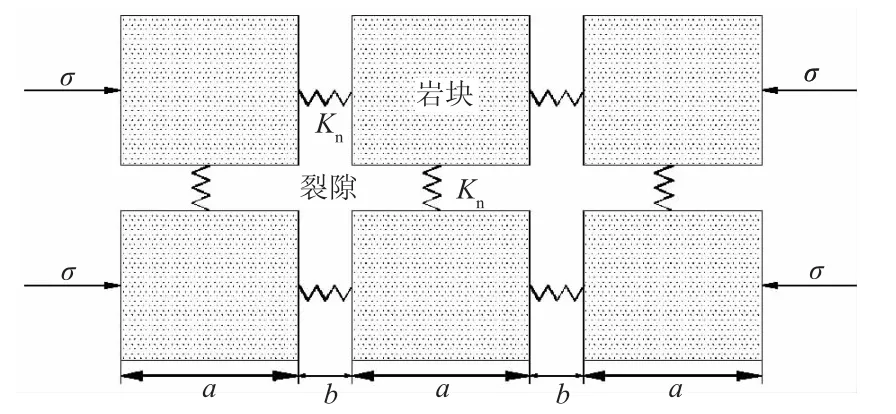
图1 断层区的物理模型Fig.1 Physical model for fault zone

岩体变形的几何方程为

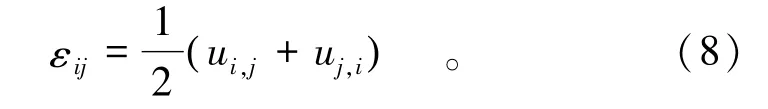
式中εij为应变张量分量；ui为位移分量。

在忽略惯性力作用,岩体的平衡方程可表示为

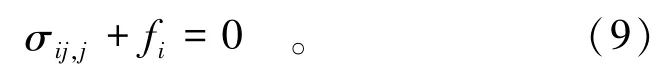
式中:σij为应力张量的分量；fi为体力的分量。

根据多孔介质弹性理论[17],表征单元体的本构方程可表示为

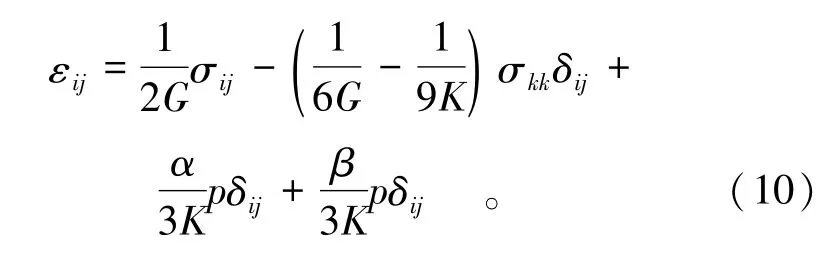
裂隙的存在将会对岩体的力学性质产生很大的影响,本文根据双重孔隙介质模型[1]中煤的弹性参数的定义对式(10)的参数进行如下定义:

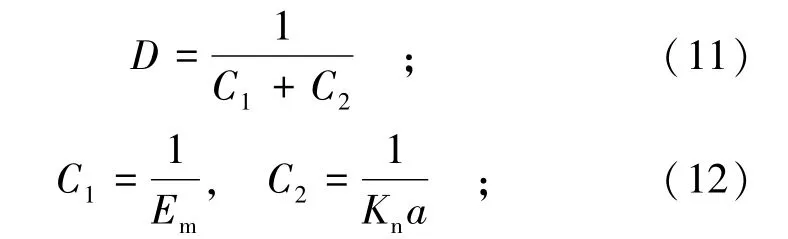
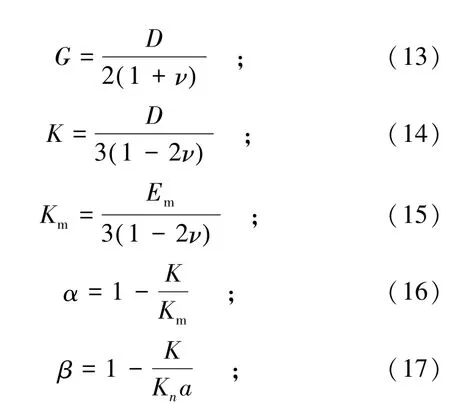
式中:Em为岩块的弹性模量；G为剪切模量；p为裂隙中流体压力；K为岩体的体积模量；Km为岩块的体积模量；Kn为单个裂隙的法向刚度；α和β分别为岩块和裂隙的Biot系数；δij为Kronecker符号；ν为泊松比。

联立式(8)至式(10),整理得到Navier型的公式为

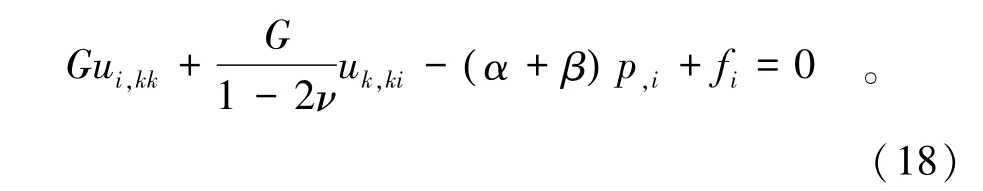
式(18)即是裂隙岩体变形的控制方程。

3.2 流体流动的控制方程

地下水在裂隙岩体中流动的质量平衡方程为

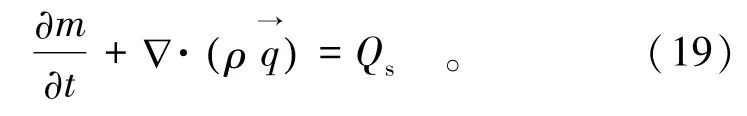
式中:m为单位体积裂隙岩体中所含流体的质量；ρ为流体的密度；为Darcy定律的速度矢量；Qs为流体的补给源；t为时间。

由于流体只在裂隙中流动,单元体内流体的质量可以表示为

式中φf为裂隙岩体的裂隙度,表示单位体积裂隙岩体中,裂隙体积所占的比值。

由前文假设可知,地下水在裂隙岩体中的流动为稳态达西渗流,根据达西定律,流体的速度矢量为

式中:k为裂隙岩体渗透率；μ为流体的动力黏滞系数。

下面探讨裂隙岩体中单元体变形特性及渗透率的表达形式。由立方定律可知,裂隙的渗透率取决于裂隙开度,岩块和裂隙的变形将会引起裂隙宽度的变化,为研究这些变化对渗透率的影响,本文从从离散裂隙网络模型中取出一个表征单元体(REV)进行研究。如图2所示,实线表示REV变形前的形态,虚线表示变形后的形态。

如图2所示REV的结构,任意方向上的变形由岩块的变形和裂隙变形组成,则

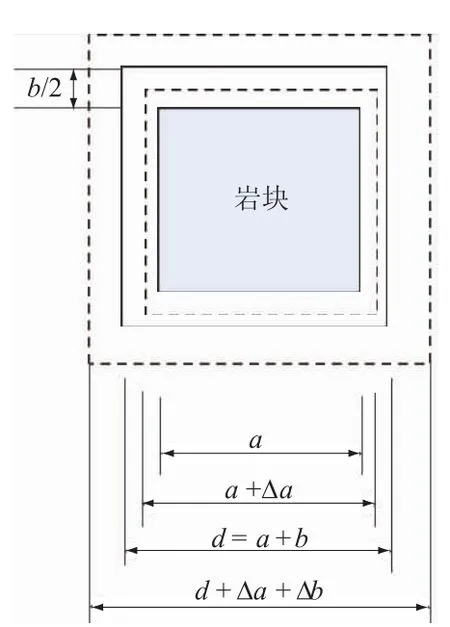
图2 表征单元体(REV)变形示意图Fig.2 Schematic diagram of deformation of representative elementary volume

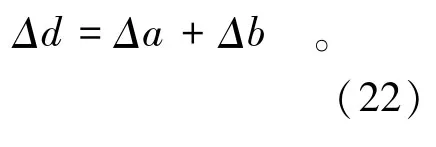
其中,

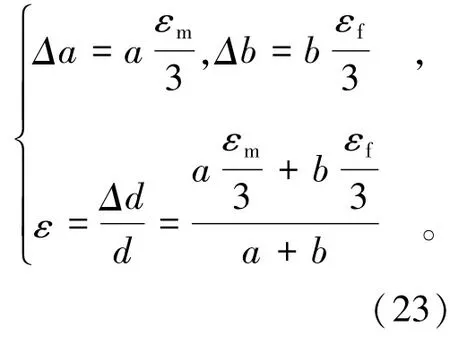
由于b≪a,则d=a+b≈a,式(23)的应变公式可变形为

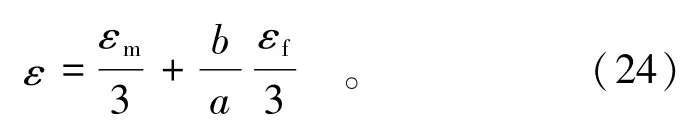
式中:d为岩块和裂隙的宽度之和；a为岩块的宽度；b为裂隙开度；ε为REV在任意一方向上的应变之和；εm,εf分别为岩块和裂隙的体积应变,其表达式分别为

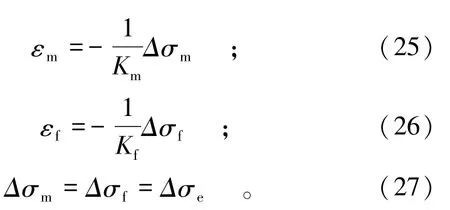
式中:Kf为裂隙的等效体积模量,Kf=a0Kn；Δσm为裂隙对岩块的作用力；Δσf为岩块对裂隙的作用力。Δσm=Δσf且与有效应力的变化Δσe是相等的。

假设在外力和流体压力的作用下,REV的体积应变是εv,则

联立以上各式得

式中:a0为岩块的初始宽度；b0为裂隙的初始张开度。

将式(29)代入式(26)得

在REV变形过程中,裂隙开度为

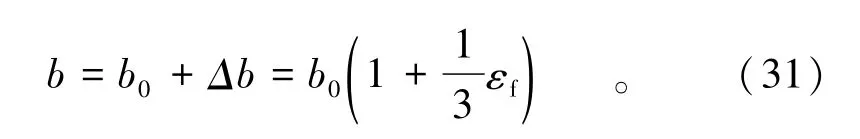
联立式(30)和式(31)得

同理:

对于如图1所示的裂隙系统,由立方定理表示的渗透率表达式[16]为

则将式(32)和式(33)代入式(34)得

表征单元体的裂隙孔隙度可以由裂隙的间距a (即岩石块的宽度)和裂隙开度b计算得到,即

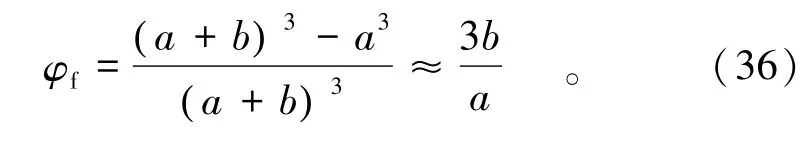
则

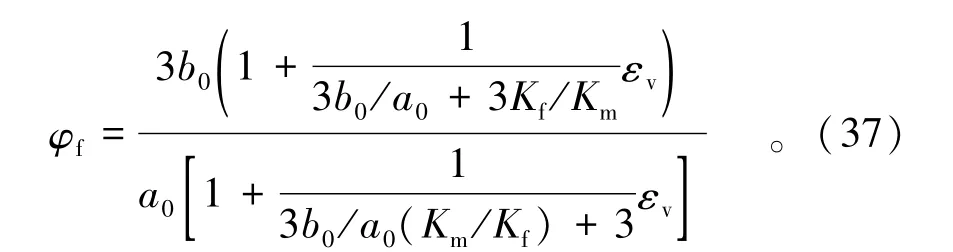
3.3 地下岩体裂隙蠕变-渗流耦合分析的控制方程

裂隙岩体变形的控制方程为

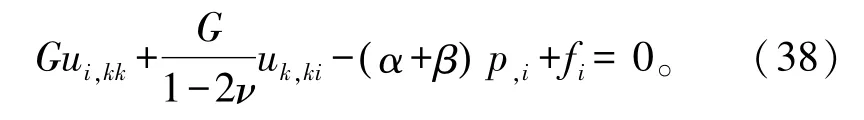
式中p为裂隙中流体压力,由流体流动的达西定律的初始条件和边界条件确定。

对于流体流动的控制方程,本文根据断层区裂隙岩体的在不同阶段具有不同的水力响应特性,将流体流动的控制方程根据时间划分成2个阶段,分别为:

(1)0≤t≤t0,地震刚过时,断层区裂隙岩体渗透率较高且还没有发生堵塞,可认为裂隙具有蠕变效应的稳态渗流,即在初期,求解域(断层区某一区域)具有完整的流通性,根据压差可自由流出边界,因此流体压力不会随时间发生变化,则有

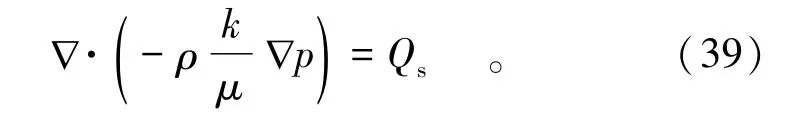
至此,建立了断层区在发生堵塞之前的蠕变-渗流藕合的控制方程。

(2)t0＜t≤t′0,裂隙经过一段时间的挤压和愈合,区域的边界被堵塞,不能发生流体的流动,此时流体具有压缩性,设ρ=c0p,则由质量守恒方程:

得流体流动的控制方程为

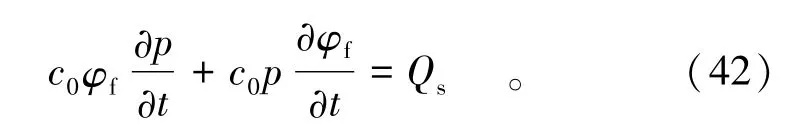
结合断层区表征单元体的变形控制方程(18)得裂隙愈合堵塞后水力响应的藕合模型。

至此,建立了地下岩体裂隙蠕变-渗流藕合的控制方程。下面探讨模型的边界条件和初始条件。

(1)对于变形控制方程,位移边界条件为

(2)对于流体流动方程,采用Dirichlet和Neumann边界条件,即:

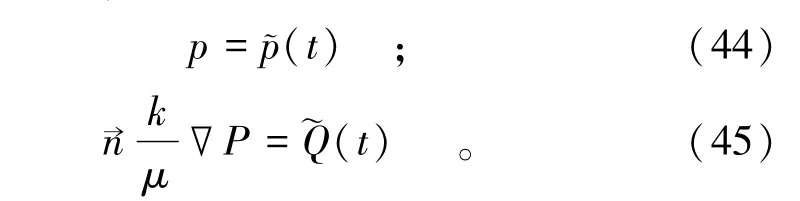
求解域位移初始条件为

式中u0是求解域的初始位移。

求解域流体压力初始条件为

式中p0是流体初始压力。

4 模型求解

本文采用COMSOL Multiphysics软件来进行数值模拟。COMSOL Multiphysics是一款大型高级数值仿真软件,因其高效的计算性能和杰出的多场直接藕合分析能力实现了任意多物理场的高度精确的数值仿真,在工程中得到了广泛的应用。本文的数值模型均是在该软件上建立并运算。

4.1 数值模型与模拟参数

如图3所示,模型尺寸为10 m×10 m,在模型的中点处设置一个圆形裂口,半径为0.01 m,其目的就是通过裂口边界的开合,决定流体的自由流通和流体堵塞在区域裂隙中。左、下、右边界为简支约束,上边界受6 MPa均布力。模型的渗流边界设置为四周均为无渗流边界,根据时间控制内部井口边界的开合,求解域内初始水压为p0=2 MPa。模型求解所需要的参数见表1。

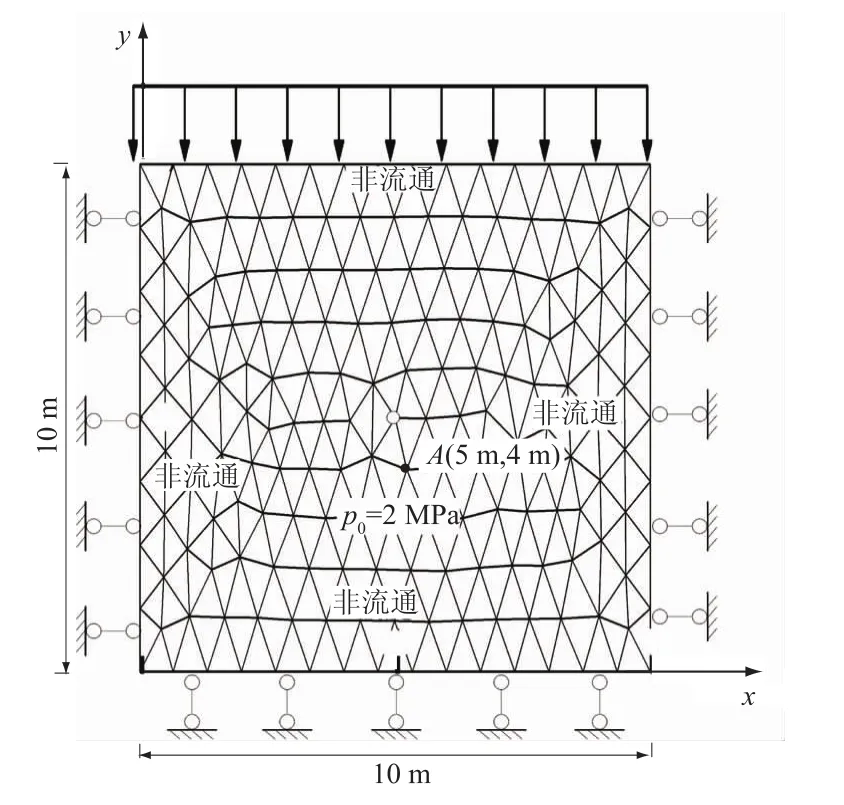
图3 数值模型Fig.3 Numerical simulation model

表1 数值模拟参数Table 1 Parameters of numerical simulation model

4.2 数值模拟结果及分析

由于求解域根据受力情况及边界条件是一个对称结构,本文只对区域内点进行分析。设置时间0≤t≤50 d时,为有蠕变效应的稳态流固藕合；50 d＜t≤1 000 d时,流体流动的边界被封堵,此时无流体运动,裂隙中流体压力随蠕变进行发生变化。

由渗透率的推导过程可知,渗透率与体应变有直接的关系,在t＞0的时间里,蠕变一直进行着,因此区域内体应变是随时间的一个变化量,区域内点A(5 m,4 m)的变化如图4所示。

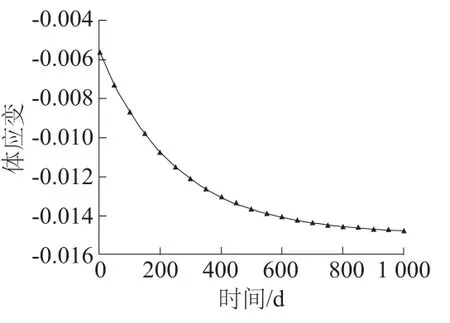
图4 求解域中A点体应变随时间的变化Fig.4 Volume strain vs.time of point A in solution domain

在t=0时刻,即裂隙蠕变效应尚未发生时,常规裂隙岩体流固藕合所产生的体应变,可认为是震后裂隙岩体的流固藕合产生的体应变。在t＞0时,蠕变发生后,由控制方程可知,体应变主要受蠕变效应的影响,蠕变时裂隙刚度是随时间的变化量,因而体应变随时间的变化关系如图4所示,可以看出在t=1 000 d时,体应变绝对值较蠕变之前增加了1倍,影响较大。由式(32)和式(35)可知,裂隙开度和渗透率均是体应变的函数,图5为观察点A(5 m,4 m)的裂隙开度和渗透率的变化曲线。

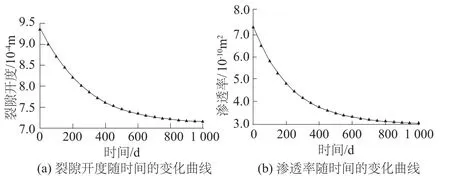
图5 求解域中A点裂隙开度和渗透率随时间的变化关系Fig.5 Fracture aperture vs.time and permeability vs. time of point A in solution domain

由图5(a)可知,当t=0时,在法向应力和孔隙压力的藕合作用下,裂隙的开度已经降低；当t＞0时,由于裂隙蠕变,裂隙开度随刚度的降低和外力、孔隙压力共同作用下,裂隙开度随时间降低,即:在裂隙愈合过程中,由于应力挤压的蠕变作用下,断层区中裂隙开度会慢慢降低；继而导致与裂隙开度密切相关的裂隙岩体渗透率的降低。由图5(b)可知,渗透率随时间降低,其曲线理应是图5(a)的三次方关系,只是图中并不能明显地表达出来。由于裂隙开度与体应变之间的线性关系,对比图4和5(a)可以发现二者随时间的变化曲线是相似的。

在前文建立模型时,设定了区域封堵的时间,限制模型求解域中流体出口,使流动不能发生,持续的蠕变会造成裂隙开度降低,其中的流体被挤压,流体压力将会发生变化。如图6所示,无论在何时进行封堵,流体压力均会增大,且从与图5(a)的对比中可以看出,流体压力的增大与裂隙开度降低成反对应关系,这些结论与文献资料中对于愈合过程中流体压力增大是相吻合的。t＜t0时,流体可根据达西定律流动,且有完整的通道,任意时刻的流固藕合并不能改变流体的压力,因此在这期间,求解域中流体压力稳定在2 MPa；t≥t0时,流体压力增大并呈相同的增长趋势,这与蠕变造成的裂隙开度降低形式不随外界有效应力变化相吻合。另外,从图6可以看出,封堵发生的时间越早,流体压力达到某一阈值的时间就会越早。在实际中,由于地震发生后,一般会有大量的琐碎岩石颗粒或者泥沙颗粒流入断层区造成封堵,这是愈合前期的封堵,会在地震过后数天内完成；另外一个封堵机制是在长期的愈合过程中,矿物质在各种物理、化学作用下结晶析出,附着在裂隙表面造成封堵,因此实际的封堵机制比较复杂难测,本节提供了一种封堵的效果模拟。

图6 不同初始封堵时间对流体压力的影响Fig.6 Influence of initial plugging time on fluid pressure

5 结 语

(1)推导了裂隙岩体流固藕合模型的一般表达式。假定本文表征单元体是由岩块和围绕着岩块的裂隙组成,其变形为基质和裂隙的变形之和,并由此建立了基于立方定理的单元体渗透率表达式。

(2)将岩体裂隙愈合现象归因于裂隙蠕变效应,并将广义Kelvin模型作为裂隙蠕变的基本模型,取得较好的效果。但是广义Kelvin模型并不能认为是深部裂隙岩体愈合的真实模型,因为在实验室条件下很难模拟深部岩体所处的应力环境及地震作用的破裂形式,而广义Kelvin模型是在实验条件下得到的,与真实的深部裂隙岩体蠕变形式必然不同。并且由裂隙蠕变表达式可知,裂隙刚度并不能无限减小,这就使得裂隙不能达到完全愈合,与真实震后岩体能够完全愈合不符,因此,探索真实的深部裂隙岩体愈合模型是未来的研究方向。

(3)本文从影响地层渗透率的机理分析,给出了综合各种地质因素的数学模型,为地震水力响应提供了合理的解释,具有重要的参考价值。

[1]RICE J R.Heating and Weakening of Faults During Earthquake Slip[J].Journal of Geophysical Research,2006, 111(B05):311.

[2]REMPEL A W,RICE J R.Thermal Pressurization and Onset of Melting in Fault Zones[J].Journal of Geophysical Research,2006,111(B09):535-540.

[3]XUE L,LI H B,BRODSKY E E,et al.Continuous Permeability Measurements Record Healing Inside the Wenchuan Earthquake Fault Zone[J].Science,2013,340: 1555-1559.

[4]MONTGOMERY D R,MANGA M.StreamFlow and Water Well Responses to Earthquakes[J].Science,2003,300: 2047-2049.

[5]WANG C Y,DREGER D S,WANG C H,et al.Field Relations among Coseismic Ground Motion,Water Level Change and Liquefaction for the 1999 Chi-Chi(Mw=7.5) Earthquake,Taiwan[J].Geophysical Research Letters, 2003,30(17):1890-1893.

[6]WANG C Y,CHIA Y.Mechanism of Water Level Changes During Earthquakes:Near Field versus Intermediate Field[J].Geophysical Research Letters,2008,35(12) :86-109.

[7]LIU W Q,MANGA M.Changes in Permeability Caused by Dynamic Stresses in Fractured Sandstone[J].Geophysical Research Letters,2009,36(20):146-158.

[8]朱 立,刘卫群,王甘林.振动对充填裂隙渗透率影响的实验研究[J].实验力学,2012,27(2):201-206. (ZHU Li,LIU Wei-qun,WANG GAN-lin.Experimental Study the Influence of Vibration on the Permeability of Fractured Sandstone with Sediment Particles[J].Journal of Experimental Mechanics,2012,27(2):201-206.(in Chinese))

[9]GEBALLE Z M,WANG C Y,MANGA M.A Permeabilitychange ModelforWater-levelChangesTriggeredby Teleseismic Waves[J].Geofluids,2011,11(3):302-308.

[10]BRODSKY EE,ROELOFFS E,WOODCOCK D,et al.A Mechanism for Sustained Groundwater Pressure Changes Induced by Distant Earthquakes[J].Journal of Geophysical Research,2003,108(B8):2390-2392.

[11]ELKHOURY J E,BRODSKY E E,AGNEW D C.Seismic Waves Increase Permeability[J].Nature,2006,441: 1135-1138.

[12]徐卫亚,杨圣奇.节理岩石剪切流变特性试验与模型研究[J].岩石力学与工程学报,2005,24(增2):5536-5542.(XU Wei-ya,YANG Sheng-qi.Experiment and Modeling Investigation on Shear Rheological Property of Joint Rock[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(Sup.2):5536-5542.(in Chinese))

[13]杨松林,张建民,黄启平.节理岩体蠕变特性研究[J].岩土力学,2004,25(8):1225-1228.(YANG Song-lin, ZHANG Jian-min,HUANG Qi-pin.Analysis of Creep Model of Jointed Rock[J].Rock and Soil Mechanics, 2004,25(8):1225-1228.(in Chinese))

[14]熊良霄,杨林德.考虑节理面法向蠕变的节理岩体蠕变模型[J].中南大学学报(自然科学版),2009,40(3): 814-821.(XIONG Liang-xiao,YANG Lin-de.Creep Model for Rock Mass Considering Normal Creep of Rock Joint Plane[J].Journal of Central South University(Science and Technology),2009,40(3):814-821.(in Chinese))

[15]HUANG T H.Elastic Moduli for Fractured Rock Mass[J]. Rock Mechanics&Rock Engineering,1995,28(3):135-144.

[16]WU Y,LIU J S,ELSWORTH D,et al.Dual Poroelastic Response of Coal Seam to CO2Injection[J].International Journal of Greenhouse Gas Control,2010,4(4):668-678.

[17]DETOURNAY E,CHENG A H D.Fundamentals of Poroelasticity[M]//FAIRHURST C.Comprehensive Rock Engineering:Principles,Practice and Projects:Vol.2.Oxford:Pergamon Press,1993:113-171.

(编辑:黄 玲)

Creep-seepage Coupled Analysis of Underground Fractured Rock Mass

CHEN Jun-guo1,2,LIU Wei-qun1,LIANG Hao-nan1
(1.School of Mechanics&Civil Engineering,China University of Mining and Technology, Xuzhou 221008,China；2.College of Mining&Safety Engineering,Shandong University of Science&Technology,Qingdao 266590,China)

Crack-healing of rock mass in fault zones after earthquake plays an important role for hydraulic response for the earthquake.In order to study the healing effect of fractured rock mass on the spatio-temporal evolution law of permeability in deep fault zones,we introduced creep effect of fracture to the network coupled model of discrete fractures.On this basis,a new spatio-temporal evolution model for fractured rock mass based on fluid-solid coupling was built,and the coupled equations were solved with the software of COMSOL Multiphysics.The results show that, before sealing,common coupled seepage achieves a steady state.Due to complete seepage channel,the fluid-solid interaction can't change fluid pressure at any given time.As sealing happens,under the influence of creep,fracture aperture and permeability of unit body decrease,but fluid pressure increases.The conclusions can provide a theoretical basis for healing mechanism of rock mass and evolution analysis of permeability in fractured zones after earthquake.

fractured rock mass；creep effect；permeability；fracture aperture；fluid-solid coupling

TU45

A

1001-5485(2015)11-0045-07

10.11988/ckyyb.20140499

2014-06-20；

2014-08-10

国家自然科学基金项目(41074040)；国家重点基础研究发展计划(973)项目(2009CB219605)

陈俊国(1981-),男,山东潍坊人,博士研究生,主要从事地下裂隙岩体渗流力学方面的研究,(电话)13406482700(电子信箱)chenjunguo2002@163.com。