基于合作博弈模型的矿产资源开发利用合作策略研究∗

吕 波芦翠杰王盼河

(1.山西博韬投资有限公司,山西省太原市,030031; 2.中国矿业大学(北京)管理学院,北京市海淀区,100083)

基于合作博弈模型的矿产资源开发利用合作策略研究∗

吕 波1芦翠杰2王盼河2

(1.山西博韬投资有限公司,山西省太原市,030031; 2.中国矿业大学(北京)管理学院,北京市海淀区,100083)

在概括我国矿产资源开发利用合作机制现状的基础上,识别矿产资源开发利用主体之间的收益分配矛盾,然后基于开展Shapley值法的矿产资源开发利用收益分配研究,最后以Shapley值法应用进行算例分析。

收益分配 Shapley值法 算例分析

1 矿产资源开发利用合作机制现状与矛盾

我国矿产资源开发利用合作机制主要表现为一种多层级的委托—代理关系。在矿产资源开发利用过程中,这种委托—代理关系中各主体利益诉求并不相同。由于不同的利益诉求,它们在合作过程中,也表现出不同的矛盾与问题。

1.1 我国矿产资源开发利用的收益分配主体

所谓收益分配主体是指在某种前提条件下获得相应份额利益的社会群体或团体,主要有矿产资源所有者——中央政府、矿产资源管理者——地方政府、矿产资源经营者——矿业企业、矿业职工、矿区居民。在矿产资源开发利用收益分配中,各主体之间的关系主要是由矿产资源开发利用过程中所涉及经济利益之间的利害关系所决定的,见图1。

图1 矿产资源开发利用收益分配主体间的关系示意图

1.2 各收益分配主体之间的矛盾

矿产资源开发利用各主体的利益结构表现为经济利益、社会利益、政治利益、生态利益的组合,见表1。各收益主体具有不同的利益偏好排序组合,核心利益不一致以及利益偏好排序组合差异,使收益主体在利益追求过程中发生利益冲突,产生利益矛盾。

表1 矿产资源开发利用收益主体利益结构表

2 基于Shapley值法的矿产资源开发利用策略研究

收益分配问题是矿产资源开发利用及运作管理中一个敏感而复杂的问题,矿产资源开发利用主体之间的收益分配是造成矛盾冲突的关键所在,因此如何进行各方主体之间的合作与收益分配,以确保各主体方的合作与目标达成,成为各方主体联盟组成和运行的一个关键问题。

Shapley值法是矿产资源开发利用合作收益分配研究很好的选择。Shapley值作为合作博弈理论中的重要概念,它用数学的方法来解决多方合作的收益分配问题。通过合作各主体对合作联盟的贡献大小,衡量成员在合作中的重要性,应用Shapley值法将合作收益在各方之间进行分配。

下面本文将从Shapley值法出发,基于中央政府、地方政府、矿业企业、矿区居民四方主体,开展基于Shapley值法的矿产资源开发利用策略研究。

2.1 矿产资源开发利用利益分配的方法——Shapley值法

假设n个合作成员组成的联盟为集合N＝{1,2,…n} ,根据各利益相关主体的在矿产资源开发利用中贡献大小的重要程度,本文对矿产资源开发利用收益的分配主要采用Shapley值法,主要是因为其更为客观合理,从集体的利益出发。在求解Shapley值时,首先应满足如下公理:

(1)对称性原理:若博弈中的两个局中人相互替代,不影响最终结果。即对任意置换π和i∈N,有:

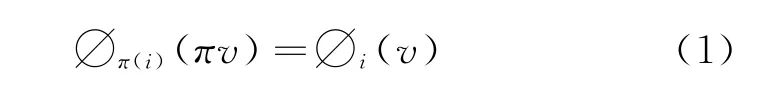
(2)若博弈中的某局中人加入联盟后未使得联盟的财富增加,则该局中人的财富为零。即:

(3)协同原理:所有成员所创造的的价值之和等于v(N),v(N)是联盟的总财富。则:

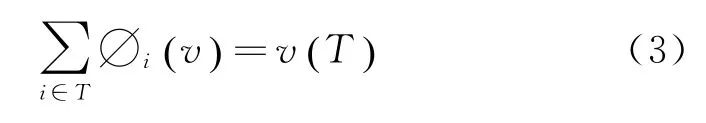
(4)可分可加性原理:两个博弈之和的值等于两个博弈值之和,对任给的两个博弈u和v,有:

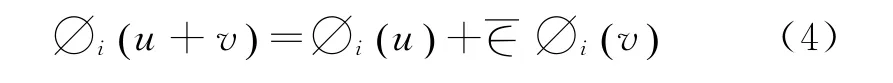
联盟的分配方案向量为∅(v)＝则存在唯一的Shapley值∅(v),有:

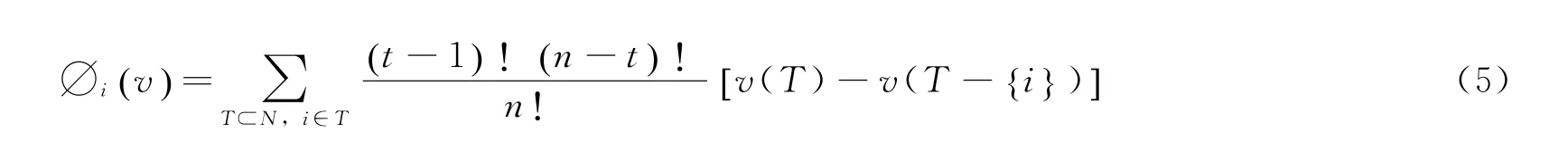
2.2 基于Shapley值法的算例分析

2.2.1 模型假设

(1)矿产资源开发利用过程中,有中央政府、地方政府、矿业企业、矿区居民四方主体N＝{1,2,3,4},合作过程中,各主体分别会获得各自的收益,同时,所获收益满足可转移支付条件。

(2)每个主体可以单独进行,也可与其他主体合作进行,只是成本较高。即满足超可加性。

(3)1个主体或2个主体合作、3个主体合作以及4个主体合作的情况下其收益如表2所示。

表2 合作收益分配表

合作收益分配表2中,净收益6表示6个单位,4表示4个单位等,表中的净收益值满足假设条件1和条件2,即净收益满足可转移支付条件和超可加性。

2.2.2 利益分配过程

用Shapley值法合理分配中央政府、地方政府、矿业企业、矿区居民四方主体之间合作收益。

表3 ∅1(v)的计算

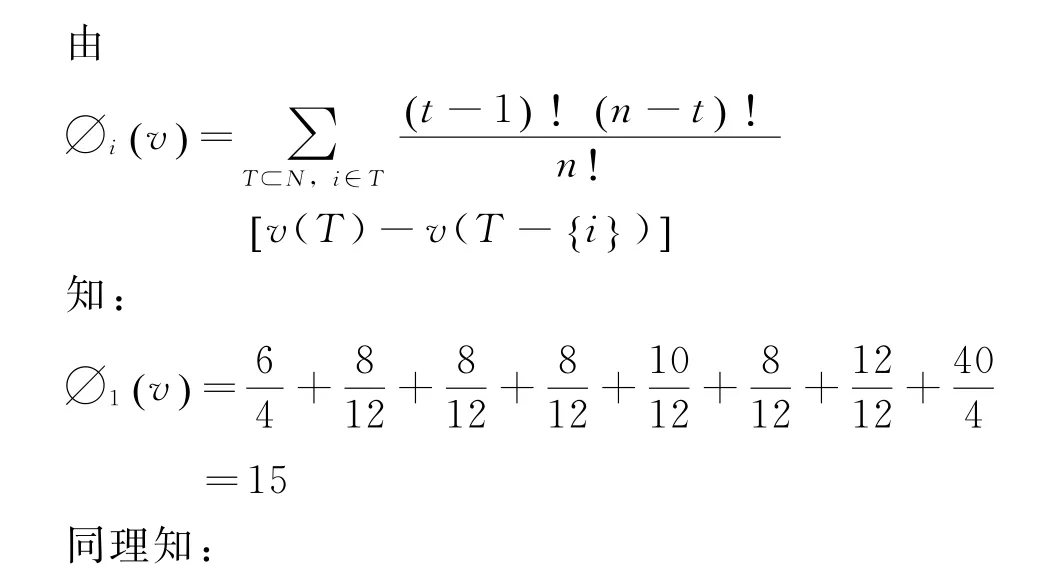
表4 ∅2(v)的计算

表5 ∅3(v)的计算

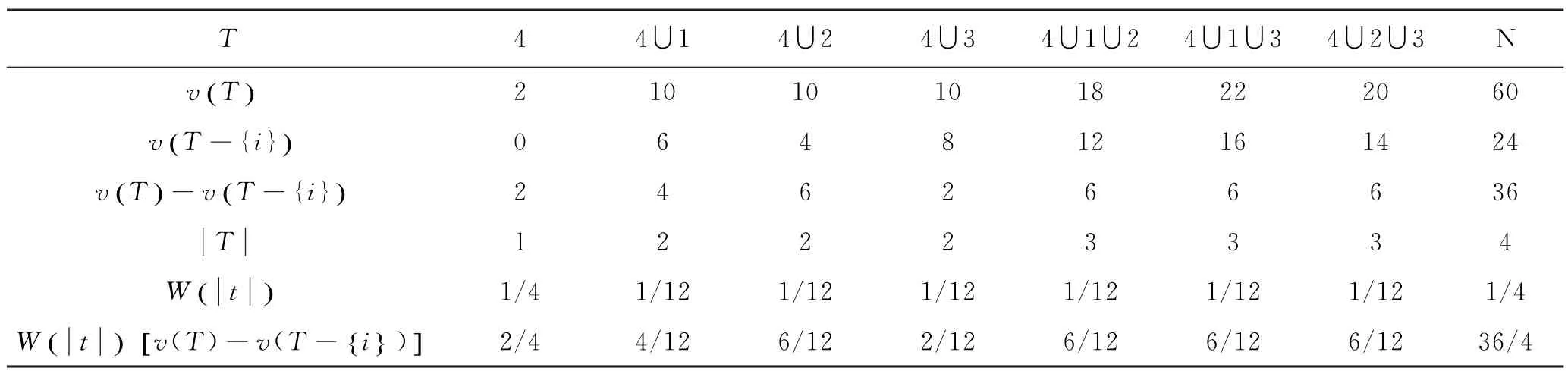
表6 ∅4(v)的计算

表7 非合作与合作的对照

∅1(v)、∅2(v)、∅3(v)和∅4(v)的计算结果分别见表3、表4、表5、表6,非合作与合作的对照情况见表7,通过表7中非合作收益一栏可知,主体1、主体2、主体3、主体4在任何两方都不合作情况下,各自的收益分别为6、4、8、2;合作收益一栏表示4个主体在四方共同合作情况下各自的收益情况,可知主体1、主体2、主体3、主体4各自的收益分别为15、14.33、17.33、12;收益变动幅度一栏表示合作情况下收益水平相对于非合作情况下收益水平的变动幅度,可知主体1、主体2、主体3、主体4各自的变动幅度分别为＋150%、＋258.25%、＋116.63%、＋500%。

3 结论

(1)通过中央政府、地方政府、矿业企业、矿区居民四方主体之间的合作,可以提高整体效益,即v({1,2,3,4})＞v({1})＋v({2})＋v({3})＋v({4}),验证了假设条件中的超可加性。即四方合作比四方主体在任何两方均不合作的情况下更有利。

(2)通过非合作收益与合作收益的对比可知,中央政府、地方政府、矿业企业、矿区居民四方主体共同合作能明显提高各自的收益,并且各自收益的增长幅度均较大。

(3)以Shapley值法作为各主体合作利益分配的依据,既与平均分配不同,也与按非合作收益的比例分配不同。Shapley值反映了各个主体在集体中的重要程度,基于Shapley值法可以分析各个主体对总体的贡献,根据各自的贡献大小分配各自在合作过程中应有的收益,从而使分配方法更加科学、有效,这对矿产资源开发利用过程中合作利益分配有一定的理论指导意义。各有关部门及相关主体可在具体实践过程中可以更多的借鉴这种模型化、量化的方法进行合作利益分配,减少经验型的分配方法。

[1] 袁莉玲.矿产资源利益共享机制下的矿山企业行为研究[D].成都理工大学,2010

[2] 颜坤林.我国矿产资源开发的利益分配机制研究[D].石河子大学,2008[3] 崔龙鹏,丰年,张传乐.淮南矿产资源态势与可持续发展战略思考[J].中国煤炭,2001(10)

[4] 李道平.论公共政策过程中的利益冲突[J].市政建设,2008(12)

[5] 刘岩.校企合作创新网络的结构模式和运行机制研究[D].河南农业大学,2011

[6] 张伟.汽车行业供应链博弈关系及收益分配模型研究[D].长安大学,2006

[7] 谭莉莉.高新技术中小企业合作创新与融资问题研究[D].重庆大学,2004

[8] 姚龙景.基于Shapley值的供应商管理用户库存收益分配模式研究[D].山东大学,2010

[10] 赵艳.基于合作博弈论的我国家电企业营销渠道研究[D].黑龙江大学,2009

[11] 刘卫.基于博弈论的虚拟共同配送系统信任机制研究[D].北京工商大学,2008

Study on the development and utilization of mineral resources cooperation strategy based on cooperation game model

Lv Bo1,Lu Cuijie2,Wang Panhe2
(1.Shanxi Botao Investment Limited Corporation,Taiyuan,Shanxi 030031,China; 2.China University of Mining and Technology,Beijing,Haidian,Beijing 100083,China)

This paper identified the income distribution conflicts of different mineral resources development and utilization subjects,based on the understanding of the mineral resources utilization cooperative mechanism status.Then the author proposed the study on the profit distribution of mineral resources based on Shapley value method,and finally applied it to numerical example analysis.

income distribution,Shapley value method,example analysis

TD－9

A

吕波(1973－),男,山西省阳泉市平定县人,山西博韬投资有限公司董事长,工商管理硕士,博士研究生在读,从事资源开发与规划的研究。

(责任编辑 张大鹏)

国家科技支撑计划项目(2013BAH12F04),天地科技工艺技术创新项目(KJ－2013－TDHT－01)