基于CFD的钻井船月池流场及附加阻力研究

李志雨 张海彬

（中国船舶及海洋工程设计研究院 上海200011）

引 言

钻井船具有较好的自航能力，机动灵活，在满足频繁的调遣需求方面具有无可比拟的优越性，其良好的可变载荷能力将有效降低远程补给的成本。钻井船是目前深海油气钻探开发的主力装备之一。由于钻井作业的需要，钻井船在靠近船舯部位设有较大的月池开口，导致其航行阻力较未开口时有明显增加，阻力增加量可占全船阻力的10%～15%，在航速较高时甚至可达100%。已有研究表明，月池附加阻力与月池内水体的振荡形式及幅度有较大的关系，而月池的形式及尺寸决定了月池内水体的振荡模式，航速决定了振荡的幅度［1］。月池内水体的振荡模式主要有沿垂向的“活塞”形式及沿纵向的“晃荡”形式［2］。对于矩形月池，“活塞”形式主要发生在短月池，“晃荡”形式主要发生在长月池。

目前主要采用模型试验方法对钻井船阻力进行研究，但在方案设计阶段，模型试验既费时又昂贵，相比之下CFD方法更经济，且可以更深入研究钻井船流场特性，分析月池附加阻力的成因，为研究月池减阻措施提供理论支持。国内外学者对月池内水体振荡现象进行了较多研究，但对月池附加阻力数值计算研究较少。Erik对二维月池流场进行了数值模拟，并分析了流场特性及通过二维月池阻力预报三维月池阻力的可行性［3］。刘学勤借助数值计算方法对两型深水钻井船阻力进行预报，形成预报深水钻井船阻力性能的方法和流程［4］。

本文应用商业CFD软件Fluent，对某钻井船航行时的流场进行模拟，预报该船的阻力性能，并与循环水槽模型试验结果进行对比分析，研究采用数值计算方法预报月池附加阻力的可行性和可靠性。

1 数学模型

船舶在静水中航行时，其流场为粘性不可压流场，可以用计算流体力学方法建立数学模型。船舶粘性流场的控制方程有连续性方程和动量方程，雷诺平均化后的控制方程为：

式中：ui为流体时均速度分量，m/s；

p为流体压强，Pa；

fi为流体体积力分量，N；

v为流体运动粘性系数，m2/s；

上述方程在求解时不封闭，需引入部分湍流方程来使其封闭。本文使用在船舶粘性流动计算中应用较广的SSTk-ω两方程湍流模型，其方程为：

式中：各符号物理意义详见文献［5］。

船体兴波及月池内流体的振荡都会对阻力产生很大的影响，因此自由液面不可忽略。本文采用VOF方法捕捉自由液面，第q相的输运方程可表示为：

式中：为第q相的体积分数，是p相到q相的质量输运，是q相到p相的质量输运，为源项。

2 数值模拟

2.1 船体及月池尺度

本文应用Fluent软件进行钻井船阻力性能数值模拟，计算中钻井船船体及月池尺度如表1所示。图1为船体及月池示意图，月池位于船舯偏后，为阶梯型月池，前部台阶高度8.4 m，后部台阶高度13.3 m。

表1 船体及月池尺度 m

图1 船体及月池示意图

2.2 计算域及网格划分

本船模型试验是在循环水槽中进行，根据水槽试验段的尺寸选定船模缩尺比为59.885 7。为了使数值模拟结果同模型试验结果具有可比性，本文进行船模尺度的流场模拟，计算域宽度和水深的选取同循环水槽实际尺寸一致，船前延伸1倍船长，船后延伸3倍船长，自由面距上边界1.5倍吃水。

采用H型结构化网格进行网格划分，对船艏和船艉部分圆弧区进行O型网格处理，以提高网格质量。距壁面第一层网格高度参照文献［6］，选取千分之一船长，对水线面附近区域及月池内部区域网格进行适当加密。船体及月池表面网格如图2所示。

图2 船体及月池表面网格

本文对裸船体流场划分了粗、中、细三组不同密度的网格，分别对三个航速进行了数值模拟，来研究不同网格密度数值分析的收敛性。相应的网格数分别为：网格1为1 548 450、网格2为2 488 710、网格3为3 332 662。

2.3 离散格式及求解算法

本文采用定常方法计算了多组航速时的阻力，采用非定常方法研究了某一流速下的月池流场特性。

采用有限体积法对控制方程进行了离散，压力项插值采用PRESTO！格式，其他项均采用二阶迎风格式离散，定常方法体积分数采用二阶迎风格式离散，非定常方法体积分数采用一阶迎风格式离散。压力-速度耦合方程采用SIMPLEC算法求解。

3 数值模拟结果及分析

为减小阻塞效应对结果的影响，根据循环水槽试验经验，运用田村法对流速进行修正，公式如下：

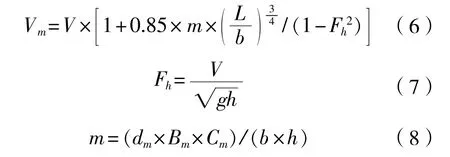
式中：b为水槽宽度，m；h为水槽深度，m；dm为模型吃水，m；Bm为模型型宽，m；Cm为模型中横剖面系数；L为模型水线长，m；V为船模速度也即循环水槽试验段的水流速度，m/s；Vm为修正后的船模速度，m/s。

3.1 网格收敛性验证

表2给出三组网格的阻力计算结果。结果显示，计算值大于试验值，且随着网格数的增加，计算值越来越接近于试验值，但相比网格数的增加，阻力的减小比例较小。考虑到增加月池模型之后网格数将大幅增加以及计算资源的限制，在本文后续计算中，裸船体阻力计算采用网格2，带月池模型的网格数接近网格3。

表2 不同网格密度阻力计算结果及试验结果

3.2 计算值与试验值对比

本文将计算结果与循环水槽试验结果进行对比，以验证数值计算结果的准确程度。

表3给出裸船体以及裸船体和月池模型的阻力计算值和试验值，可见各流速下裸船体阻力的计算值比试验值偏大，误差在3%～7%之间；而带月池的阻力计算结果在流速较低时偏大，流速较高时偏小，误差在8%以内。由于月池内流动较复杂，用定常方法计算的误差在8%以内是可以接受的。

表3 数值计算与模型试验所得阻力值的对比

3.3 月池流场及附加阻力分析

3.3.1 月池流场分析

钻井船在航行过程中，月池内流体为非定常流动，虽然定常方法能较好地预报阻力，但不能准确模拟月池内部流体的非定常特性；因此本文对Fr=0.139 时的月池流场进行了非定常研究。

图3-图6为月池内水体呈现周期流动时的几个典型速度矢量图，其中横剖面位于120号肋位，纵剖面为中纵剖面，模拟流动时刻分别为19.05 s和19.40 s。由纵剖面图可以看到，船底处水流流经月池时携带月池底部水体一起向后移动，于是月池内前壁上部的水向下补充，月池内上部的水向前流动，月池后壁的水向上运动，形成了月池内的漩涡；自由面的变化主要由月池内漩涡及台阶前壁反射的波叠加而成，波面升高幅度与试验观察结果较为接近；月池内外水体质量交换在纵向上主要发生在月池开口后方靠近后壁处。由横剖面图可以看到，在月池开口侧边会有流动分离，生成不完全对称的两个小漩涡，发生质量交换；月池内靠近自由面处也有漩涡运动；横向流动的不对称以及在月池开口侧边的质量交换是月池三维效应产生的主要原因，导致二维月池计算结果与试验结果相比存在较大误差。

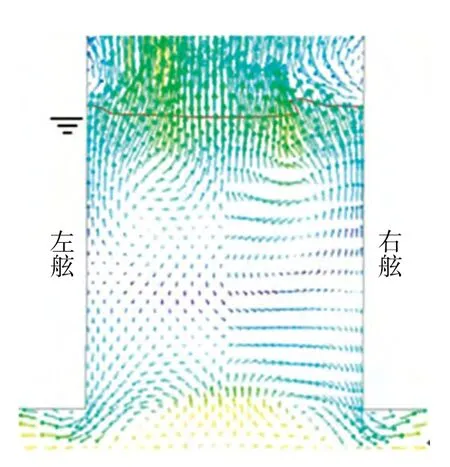
图3 横剖面速度矢量（19.05 s）

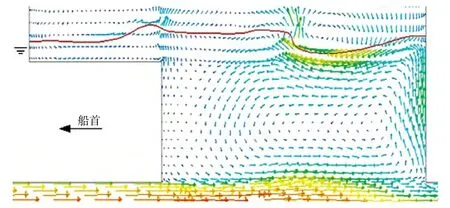
图4 纵剖面速度矢量（19.05 s）

图5 横剖面速度矢量（19.40 s）

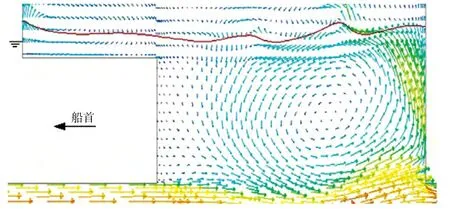
图6 纵剖面速度矢量（19.40 s）

本文研究的月池开口长宽比为2.57，属长月池，加之前部台阶平面在水面以下，致使月池内水体运动以前后晃荡为主。船底水流为月池内漩涡运动提供能量，随着月池内自由面的晃荡和水体的垂荡，月池内外水体质量产生相互交换，改变了月池附近船体流场和压力分布，月池附加阻力则由此产生。

图7给出月池的受力时历，可以看到，月池受力稳定后呈现周期特性，并可得到其周期为0.792 s。图8为试验中月池中部浪高仪记录的波面升高时历以及经过傅立叶变换后的波面幅值谱，得到其固有频率为1.399 Hz，即其固有周期为0.715 s。比较两者可知，计算得到的月池受力周期比试验得到的波面升高周期偏大（但较为接近）；因此可认为实际波面升高周期同月池受力周期相同。

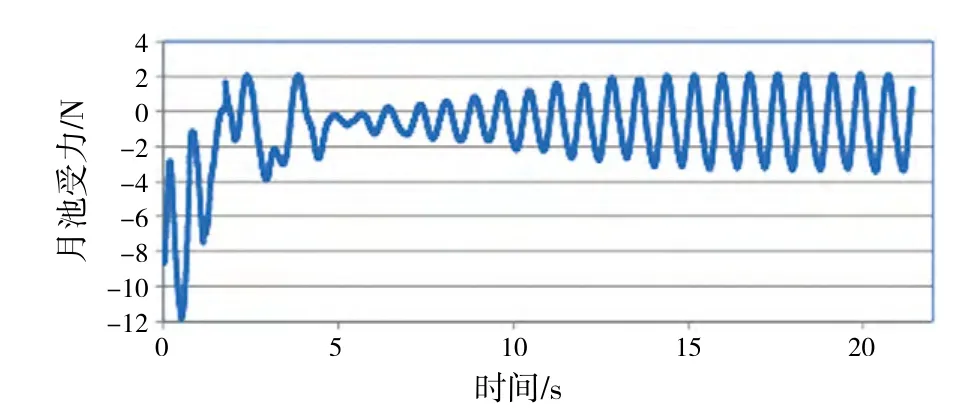
图7 月池受力时历（计算结果）

图8 波面升高时历及波面幅值谱（试验结果）

3.3.2 月池附加阻力分析

将试验和计算得到的阻力值换算到实船阻力，得到实船阻力曲线，如图9所示。可以看到有月池的实船阻力曲线在裸船体实船阻力曲线上方，且随着航速的增加，阻力增加量逐渐变大。因数值计算结果与试验结果仍有一定的差异，本文用模型试验的结果来分析月池附加阻力。

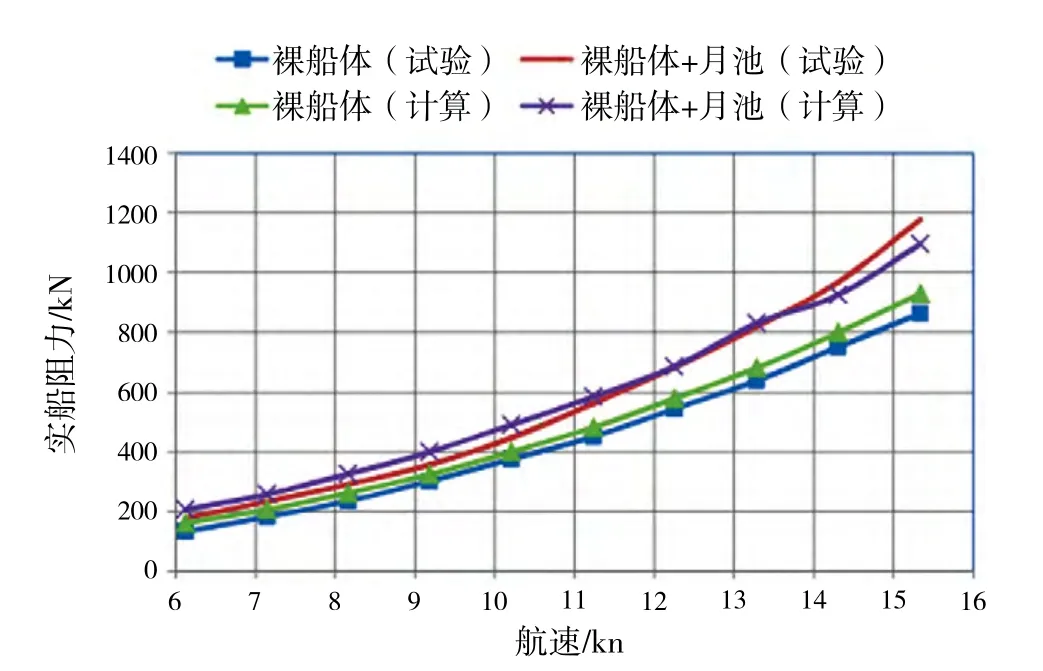
图9 实船阻力曲线

图10为由月池引起的阻力增加百分比曲线，包含本文研究的阶梯型月池及与阶梯型月池开口尺寸相同的常规直壁型月池。对于阶梯月池，随航速的增加，阻力增加百分比先减小，10 kn之后阶梯式逐步增大。对直壁型月池，阻力增加百分比曲线在7 kn附近出现一个极大值，9 kn之后出现一个极小值，阻力增加幅度比阶梯型月池高出很多，尤其在10 kn之后，两者差别随航速增加越来越明显；试验中观察到直壁型月池在7 kn时月池内水体以“活塞”振荡形式为主，之后变为前后“晃荡”形式，造成该曲线有两个比较明显的极值。

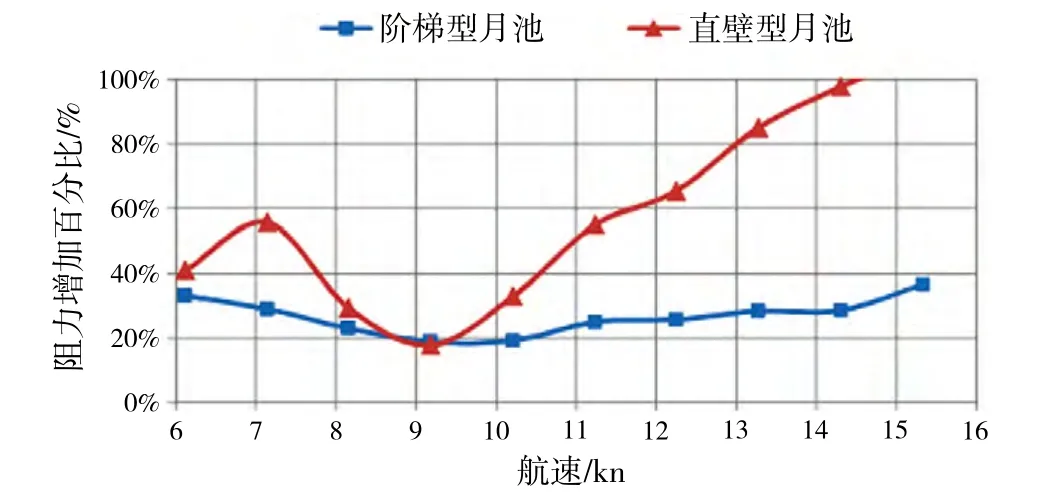
图10 阻力增加百分比曲线（试验结果）

本文研究的阶梯型月池较直壁式矩形月池有更好的阻力性能。略低于水面的前部台阶可减缓月池内水体的晃动幅度，从而减小月池的附加阻力。

4 结 论

本文采用数值分析与模型试验相结合的方法对某钻井船月池流场和附加阻力进行研究，研究结果表明：

（1）定常方法预报的钻井船阻力与试验结果较为吻合，证明该方法可以应用于月池附加阻力的数值预报。

（2）非定常方法可以模拟月池内流体的非定常特性，船底水流分离及月池内外水体质量交换维持了月池内的周期性漩涡运动，改变月池附近船体流场及压力分布，这是月池附加阻力产生的主要原因。

（3）对于传统月池形式，本文研究的阶梯型月池具有更好的阻力性能。

［1］ Riaan van’t Veer，Haye Jan Tholen.Added Resistance Of Moonpools In Calm Water ［C］//Proceedings of the ASME 27th Internactional Conference on Offshore Mechanics and Arctic Engineering.2008.

［2］ Fukuda.Behavior of water in vertical well with bottom opening of ship and its effect on ship motions ［J］.Journal of the Society of Naval Architects of Japan，1977，141 ：107-122.

［3］ Erik Hammargren，John Tornblom，Effect of the Moonpool on the Total Resistance of a Drillship ［D］.MSc Thesis Chalmers University of Technology，2012.

［4］ 刘学勤.深水钻井船水动力性能研究［D］.上海：中国船舶及海洋工程设计研究院，2013.

［5］ ANSYS.Ansys Fluent Theory Guide［R］.2012.

［6］ 张志荣，李百齐，赵峰.船舶粘性流动计算中的湍流模式应用比较［J］.水动力学研究及进展（A辑），2004（5）：637-642.