FSC赛车车架结构有限元分析
2015-01-03孙博文韩忠浩王晓怡胡振凯
孙博文,韩忠浩,王晓怡,胡振凯
(辽宁工业大学,辽宁 锦州 121001)
FSC赛车车架结构有限元分析
孙博文,韩忠浩,王晓怡,胡振凯
(辽宁工业大学,辽宁 锦州 121001)
车架是汽车的重要组成之一,它必须满足在各种工况下的强度和刚度要求,车辆才能正常行驶。对赛车而言更是如此。本文首先建立了辽宁工业大学2014年赛车车架的三维模型;然后导入到ANSYS workbench软件中,建立有限元模型,通过对有限元模型进行约束、加载,来模拟赛车在各工况下的运行情况;最后查看计算结果,判断车架是否满足要求。因此,各工况的强度、模态分析结果,对赛车的安全以及保证正常行驶具有重大意义。
FSC赛车车架;强度及刚度分析;模态分析;有限元分析
CLC NO.: U463.3 Document Code: A Article ID: 1671-7988(2015)03--
引言
中国大学生方程式汽车大赛(简称FSC)是由各高等院校汽车专业的在校学生组队参与设计与制造的比赛。所设计的赛车需满足大赛规则要求。
赛车车架作为各部件的安装载体,其安全性是赛车能否行驶的保证,也是保护车手安全的前提。本文利用Ansys workbench对车架模型进行有限元分析。
1、赛车车架模型的建立
赛车车架是按照FSC大赛规则设计的空间桁架,是由壁厚不同、长短不同的钢管焊接而成的。所设计的车架结构需要满足两方面的要求:(1)车架要有一定的强度和刚度来装配赛车上的其他总成;(2)车架的固有振动频率需要能避开各种激励频率,得到合理的动态特性,避免发生共振[1]。本文利用CATIA软件建立车架模型(如图1)。
2、赛车车架有限元模型的建立
2.1 模型修复
将已建立的车架模型导入到ANSYS workbench软件中,可以看到有的连接杆件之间产生了缝隙(如图2),这将导致划分的网格出现节点不共享的现象(如图3),从而影响接下来的分析。
这样的连接关系与实际不符,应对模型进行修改。利用Joint工具可将杆件连接起来。对修复后的模型进行分网,发现模型中网格节点共享(如图4),符合实际。
2.2 材料选择以及网格划分
由于4130钢具有高强度和高韧性,所以本车架采用此材料。4130钢材料属性主要有密度7.85×103kg/m3,弹性模量211GPa,泊松比0.279,屈服极限785MPa。
考虑到网格精度和计算时间的平衡问题,所以在划分网格时,单元尺寸选定为5mm,单元类型选用壳单元进行分网。单元形态是以大量四边形网格为主,以少量三角形网格为辅组成的。并根据杆件设定厚度。最终得到了车架的有限元模型(如图5)。整个车架的共划分为112540个单元及110081个节点。
划分好的网格需要对它的质量进行检查,高质量的网格会得到高质量的结果。Workbench中对网格质量的检查项目主要有:Element Quality、Skewness、Aspect Ratio。这些检查项目代表的意义如表1。查看本车架的网格质量检查项目(图6),可以看出所划分的网格满足各检查项目的要求。
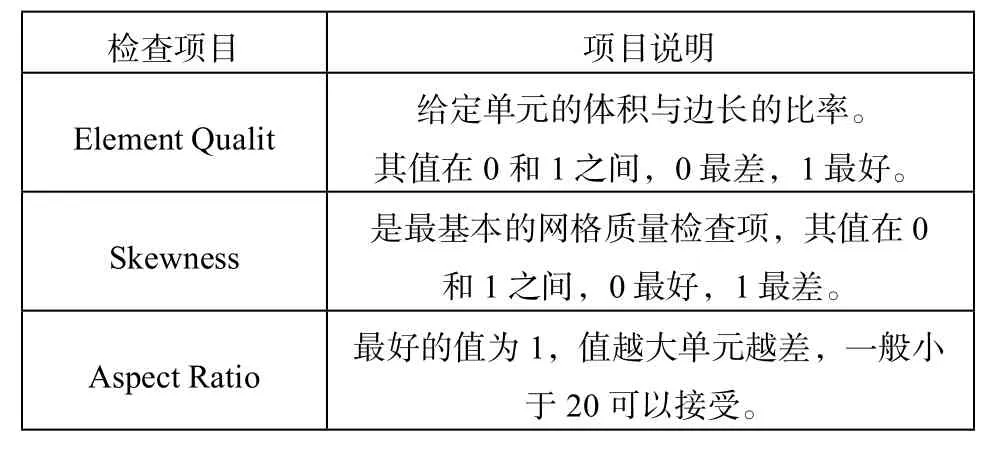
表1 [2]work bench中网格检查项目及说明
3、车架的强度分析
根据国家标准 GB/T 13043—1991 中规定∶ 样车必须以一定车速在各种道路上行驶一段里程。 典型工况是高速道路、强扭转道路和一般道路及弯曲道路上的弯曲、扭转、紧急制动和急转弯等 4 种工况[3]。本文将对上述4种工况进行模拟,验证车架的强度是否符合要求。
3.1 车架的静态载荷
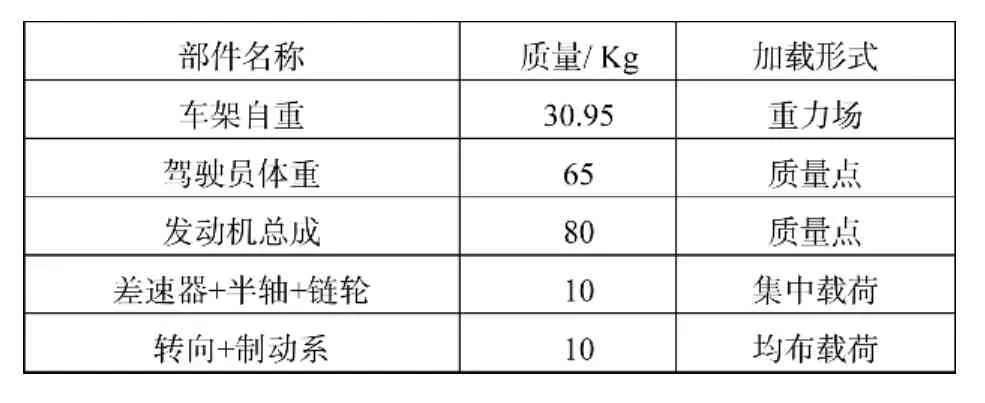
表2 各部件的质量及加载形式
车架所受到的静态载荷指的是作用到车架上各部件所产生的重力。主要包括车架自重、驾驶员体重、发动机总成质量等。将所有质量换算为重力,施加到车架的相应位置上。各部件的质量及加载形式如表2所示。
3.2 弯曲工况
弯曲工况指的是赛车在水平良好路面上匀速直线行驶或静止状态。为更好的对工况进行模拟,需将静载荷乘上一个动载系数,一般为2.0~2.5,本文取2.0。
约束情况:以赛车前进方向为X轴,横向为Y轴,垂直方向为Z轴。对前悬架右连接点进行固定约束,对前悬架左连接点进行X、Z方向的约束,对后悬架左、右连接点处进行Z方向的约束。
经过加载和约束后,运行程序进行计算,并得到相应的应力云图和位移云图。结果如图7、图8所示。从图7中可以看出最大应力为169MPa,发生在车架前环底部多杆焊接处,小于屈服极限。从图8可以看出最大位移量为1.26mm,发生在座舱底部交叉杆处。因此,弯曲工况下的车架强度满足要求。
3.3 扭转工况
扭转工况指的是一侧车轮悬空时,所受到的扭矩使车架产生扭转现象。本文模拟前悬架左侧连接点施加向上647N的集中力,前悬架右侧连接点施加向下647N的集中力。实践表明,车架承受最剧烈的扭转工况是在汽车低速通过崎岖不平路面时发生的。由于车速较低,故取动载系数为1.5[4]。
约束情况:对后悬架左连接点进行固定约束,对后悬架右连接点进行X、Z方向的约束。释放前悬架的连接点。
计算得到扭转工况下的应力、位移云图。结果如图9、图10所示。
从图9可以看出最大应力为119MPa,发生在座舱底部多杆连接处。从图10可以看出最大位移量为0.94mm,发生在座舱底部的交叉杆上。因此,车架在扭转工况下满足要求。
3.4 制动工况
制动工况指的是刹车的情况。赛车在行驶过程中需要频繁的制动,驾驶员和发动机除了受到垂直方向的载荷外,还受纵向惯性力的作用[5]。此惯性力通过设置惯性加速度a=1.4g方式进行加载,其方向沿纵向向前。
约束情况:对前悬架左、右连接点进行固定约束,对后悬架左、右连接点的Y、Z方向进行约束。
从图11可以看出最大应力为164MPa,发生在主环座舱底部多杆相交处,小于屈服极限。从图12可以看出最大位移量为0.81mm,发生在座舱底部相交杆处。因此,车架在制动工况下强度满足要求。
3.5 急速转弯工况
赛车在转弯行驶时,车架除了受到静态载荷的作用外,还会受到由于转弯产生的离心力作用。本文模拟赛车向左转弯,离心加速度为10.9m/s2,沿横向向右。
约束情况:对前悬架左、右连接点进行固定约束,对后悬架左、右连接点的X、Z方向进行约束。
从图13可以看出,最大应力为205.69Mpa,发生在座舱底部交叉杆与侧防撞杆的交叉位置。图14中最大位移为0.99mm,发生在座舱交叉处。满足要求。
4、刚度分析
刚度表示车架在外力下抵抗变形的能力,也是衡量车架性能的重要指标。
4.1 车架的弯曲刚度
为了节约计算时间,可将车架简化成图15所示简单的梁结构。把集中载荷1471.5N分别作用到车架两侧的纵向中点位置,方向垂直向下。约束情况与弯曲工况相同。通过计算得到位移云图(图16),从中找到最大位移量。
从图16中得到Z方向的最大位移量为0.48mm。将所有数据带入下列公式(1)中,就可算出车架的弯曲刚度。
F—集中载荷,N
L—车架前后悬架间的距离,m
f—加载点的挠度,m
本车架的弯曲刚度为2.37× 105Ng m2,查阅相关资料发现本车架的弯曲刚度合理。
4.2 车架的扭转刚度
将车架前舱视为如图17的梁结构,左悬架连接点施加-647N的集中载荷,右悬架连接点施加647N的集中载荷。约束同扭转工况相同。运行程序,从位移云图可以查看到最大位移量为0.39mm(图18)。
根据扭转后的最大位移量和前舱宽度B可以求出扭转角θ
根据施加集中载荷F和前舱宽度B可求出转矩T
根据转矩T和扭转角θ可求扭转刚度E
本车架的扭转刚度为1302.7Ng m/°,查询国外赛车设计资料可知,大多是扭转刚度在1000~4000Ng m/°[3]。本车架的扭转刚度在此范围内,因此合理。
5、车架的模态分析
赛车在行驶时,会受到来自路面不平度、发动机振动以及轮胎动态不平衡的激振。如果这些激振的频率与车架的固有频率相接近,则会发生共振,导致车架破坏。因此,分析车架的固有频率和振型是有必要的。
利用modal模块对车架进行模态分析,首先对模型进行分网,然后设置所要分析的阶数,运行程序得出所需要的频率和振型。车架的固有频率及振型特点如表3所示,第一阶的固有频率接近0,记录非零频率开始的六阶频率。
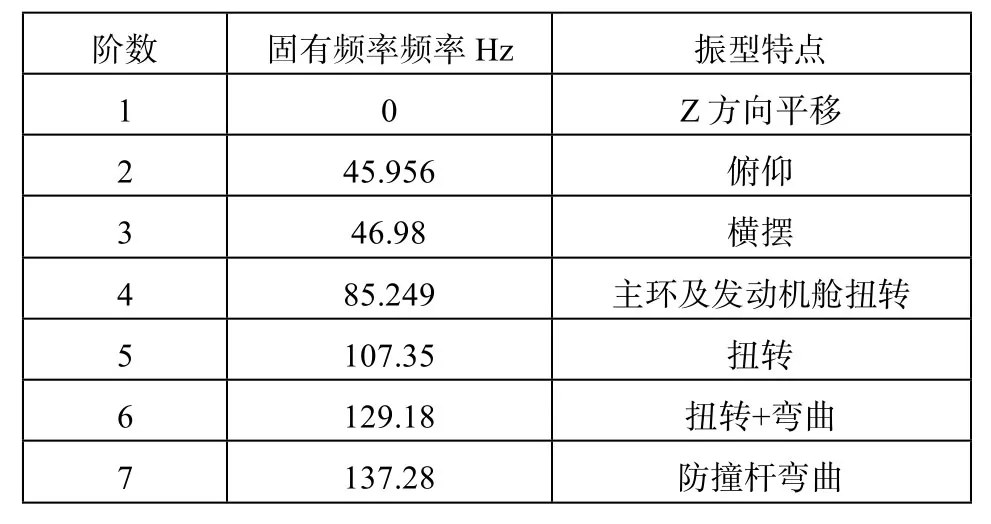
表3 模态分析固有频率及振型特点
激振中由于路面不平的频率一般为1~20HZ,车轮不平衡引起的频率一般低于11HZ。本赛车采用的发动机最高转速为12500r/min,常用转速为5000~7000r/min,怠速为2000r/min。根据发动机频率计算公式
z——发动机缸数;
τ——发动机冲程数
n——发动机转数。
由公式(5)可知常用发动机引起的激振频率为167~233HZ,怠速频率为66.7HZ。发动机怠速频率介于第三阶与第四阶频率之间,而所有频率都小于发动机常用频率范围。因为车架的振动频率避开了激振的频率,所以本车架安全可靠,不会有引起共振的危险。
6、结论
通过对辽宁工业大学2014年赛车车架进行强度、刚度和模态分析,得到了车架在4种工况下的应力、位移云图与弯曲、扭转刚度,以及车架的前6阶固有频率。结果表明,本车架在强度方面,能够抵抗破坏,满足安全要求;在刚度方面,能够抵抗变形,保证性能良好;在模态分析方面,车架的频率避开了激振的频率,避免了车架发生共振破坏的危险。同时可在结果中找出强度、刚度的富裕部位,为车架的优化设计提供理论依据。
[1] 周永光,阳林,吴发亮.FSAE 赛车车架结构优化和轻量化[J].农业装备与车辆工程,2012.
[2] 贺绍华.赛车轻量化系统方法与车架优化[D].广东:广东工业大学,2013.
[3] 赵帅,隰大帅,王世朝,陆善.FSAE赛车车架的强度和刚度分析[J].计算机辅助工程,2011.
[4] 刁秀永,鲁植雄,钟文军,谢鹏.基于ANSYSWorkbench的FSAE车架有限元分析[J]. 农业装备与车辆工程,2013.
[5] 乔邦. 基于有限元分析的大学生方程式赛车车架结构强度优化[D].河南:河南科技大学.
The Finite Element Analysis of FSC Racing Frame Structure
Sun Bowen, Han Zhonghao, Wang XiaoYi, Hu Zhenkai
(Liaoning University Of Technology, Liaoning Jinzhou 121001)
A frame is the main component of a vehicle. It must meet the requirements of strength and stiffness under driving conditions.the vehicle can be driven normally. Thus, it is also important to the racing car. In this paper, the author firstly established the three-dimensional frame model of the racing car of Liaoning University of Technology in 2014. Then establishing the finite element model by importing the frame model to ANSYS workbench software and simulating the racing car under different conditions by adding constrain and loads to the model. At last, determining the frame whether the simulation result fulfills its purpose. Therefore, the analysis of the strength and modal under different conditions is very meaningful for the safety and normally driving of the car.
FSC Racing Frame; strength and stiffness analysis; modal analysis; finite element analysis
U463.3
A
1671-7988(2015)03--
孙博文,就职于辽宁工业大学,汽车与交通工程学院。
