带权值参数的两两组合测试用例集生成算法

李龙澍，王雅婷

(安徽大学计算机科学与技术学院，合肥230601)

1 概述

在整个软件开发生命周期中，软件测试是非常重要的一个环节，是保证软件质量、提高软件可靠性的重要手段。研究表明，有20% ～40%左右的软件故障是由某个系统参数引发，20% ～40%左右的故障由某2个参数的相互作用引发，而大约70%的软件故障是由1个或2个参数的作用引起的［1］。所以，对各种待测软件系统而言，两两组合测试是一种科学、实用而有效的测试方法［2］。

目前国内外在两两组合覆盖的测试数据生成方面已有广泛研究，主要有以下算法:正交拉丁方算法［3］，Williams 算法［4］，Kobayashi算法［5］，AETG 算法［6-7］，IPO 算法［8-11］，PSST 算法［12］等。但这些算法都是致力于如何减小测试集的规模，并未考虑到参数带权值的实际要求。参数被赋予权值基本有2种情况:(1)因参数重要程度不同而赋予相应权值;(2)因生成的测试集过大而无法完全执行测试用例时，赋予参数权值以使生成的测试用例带有权值和，然后根据权值和可以优先执行比较重要的测试用例。前者是对待测系统硬性要求的处理，后者则为测试人员如何选择测试用例提供了重要依据。因此，本文在研究逐参数(In-Parameter-Order，IPO)扩展策略的基础上，考虑待测系统参数被赋予权值的情况，提出一种参数带权值的两两组合测试用例集生成方法。

2 基本概念及相关定义

假设待测系统SUT(Software Under Testing)的n个输入参数集合 X={x1，x2，…，xn}，其中每个输入参数对应的取值域为Dj(j∈［1，n］)，即每个输入参数有|Dj|个互异的取值。

定义1(测试集) 设集合 T={t1，t2，…，ti}，如果对 ti∈T，有 ti={ti1，ti2，…，tin}，且 tij∈Dj(j∈［1，n］)，则称集合T为待测系统SUT的一个测试集，ti为待测系统SUT的一条测试用例。

定义2(两两组合测试集) 设 T为待测系统SUT的一个测试集，如果对X中不同参数之间的任一两两取值组合(y，z)，都至少存在一个ti∈T，满足y∈ti且z∈ti，则称T为待测系统SUT的一个两两组合测试集。

定义3(参数需求度) 设 ti={ti1，ti2，…，tij}，其中tij∈Dj(j∈［1，n))，为已有测试集中的一条测试用例，x1，x2，…，xj为已扩展参数，将其作为待扩展参数xj+1进行组合时的可选参数，定义每个已扩展参数相对于待扩展参数的参数需求度为:

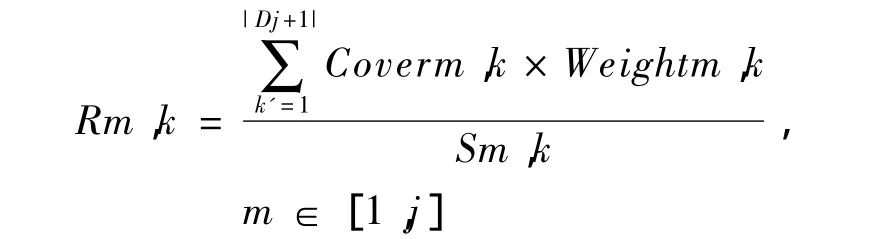
当待扩展参数的值 Dj+1，k’(参数值集 Dj+1中的第k’个取值)与已扩展参数的值Dm，k(参数值集Dm中的第 k个取值)的组合未覆盖时，Coverm，k取1，已覆盖则取 0;Weightm，k为该组合的权重值;Sm，k等于已有测试集中Dm，k的总个数。

3 IPO算法影响因子分析及改进

IPO算法是一种逐参数扩展进而生成两两组合覆盖测试数据的方法。其核心步骤为水平扩展和垂直扩展两部分，但在扩展次序和参数取值上，该算法并未考虑到有关影响因子对算法性能的影响。所以，本文从扩展次序和参数取值上出发，分析对算法性能可能产生影响的有关因子，并分别对影响因子做出合理的改进。

3．1 待扩展参数的扩展次序

IPO算法中第一个扩展次序问题，即待扩展参数的扩展次序。该算法在选择一个未扩展参数作为扩展对象时，采用了随机次序进行扩展，并未考虑参数次序不同而可能产生的不同影响。本文考虑在根据某些因素对待扩展参数进行排序后，再按照此顺序逐一扩展参数。

定义4(参数值的权值) 为每个参数取值Di，k(参数值集Di中的第k个取值)赋予一个数值Wi，k(－1．0≤Wi，k≤1．0)，其中，－1．0 表示优先级最低;1．0表示优先级最高，这个Wi，k就称为该参数值的权值。

为每个参数取值赋予一个权值 Wi，k后，对可选参数进行排序的步骤如下:

(1)计算参数值两两组合的组合权重值

当参数 xi取值为 Di，k，参数 xj取值为 Dj，k’，则两两组合(Di，k，Dj，k’)的组合权重值为 Wi，k× Wj，k’。参数x1取1，参数x2取5，则两两组合(1，5)的组合权重值为 W1，2× W2，2=0．2 ×0．2=0．04。

(2)计算两参数间权值和

两参数间权值和为该两参数所有取值两两组合的组合权重值之和，计算公式为:

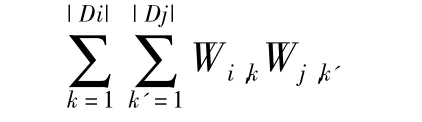
如参数(x1，x3)两参数间权值和为Wj，k'=0．4 × 0．2+0．4 × 0．5+0．2 × 0．2+0．2 ×0．5+0．3 × 0．2+0．3 × 0．5+0．1 × 0．2+0．1 ×0．5=0．7。同理，得(x1，x2)，(x2，x3)两参数间权值和分别为0．9，0．63。参数和参数取值及参数值权值的输入如表1所示。其中，括号中的数值为该参数值的权值。

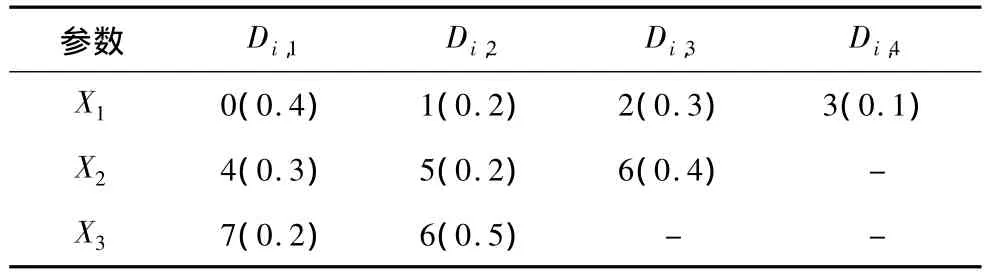
表1 参数和参数取值及参数值权值的输入

(3)计算各参数的权值总和

每个参数的权值总和等于该参数与其他参数的两参数间权值和的和。例如，上述例子各参数的权值总和如表2所示。

表2 各参数的权值总和

最后，根据各参数的权值总和的大小按降序进行排序，得到待扩展参数的扩展次序。例如，上述例子的扩展次序为:x1，x2，x3。这种排序过程适用于参数值带权值的情况，若参数值未被赋予权值，则可直接根据参数取值个数|Dj|按降序对待扩展参数进行排序。

3．2 已有测试集的扩展次序

IPO算法中的第2个扩展次序问题是在选定待扩展参数后，需要对已有测试集中的测试用例进行水平扩展，即已有测试集的扩展次序。IPO算法对该扩展次序并未做任何处理，只是按照原本的已有测试集次序进行扩展［13］。所以，本文在考虑不同的扩展次序可能生成不同的测试集结果的基础上，根据有关影响因子对已有测试集中的测试用例进行排序，过程如下:首先根据定义3中参数需求度的概念，计算已有测试用例的需求度R:

当参数值未被赋予权值时，则Weightm，k=1，可以进一步简化公式。然后，根据已有测试用例的需求度R按从大到小降序的顺序进行排序，得到已有测试集的扩展次序。

3．3 待扩展参数的取值选择

IPO算法中参数取值问题，是指在进行水平扩展时，为待扩展参数选取一个参数值，即待扩展参数的取值选择。该算法只是将待扩展参数 xj+1的|Dj+1|个可选值依次扩展到已有测试集中，若此时仍有可选值未被扩展，则未扩展完的可选值直接进入垂直扩展步骤;反之，则继续选择覆盖率较大的可选值进行赋值，直到完成水平扩展［13］。在此参数取值问题上，本文同样根据某些因素进行选择，具体过程如下:

(1)计算参数值的权值贡献

依次选取待扩展参数的参数值，然后计算所选取参数值对应的权值贡献。计算公式为:

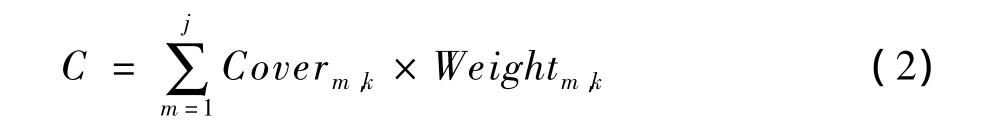
其中，Coverm，k和 Weightm，k的约束如同定义 3 中一样。

在这个计算过程中，有一种特殊情况，就是扩展的两两组合包含了前面测试用例所覆盖过的两两组合，那么此两两组合所对应的Coverm，k=0，即此两两组合所对应的参数值两两组合的组合权重值不计入该参数值的权值贡献。

(2)为待扩展参数选取参数值

比较每个参数值所对应的权值贡献，选取使权值贡献达到最大的那个参数值作为此测试用例待扩

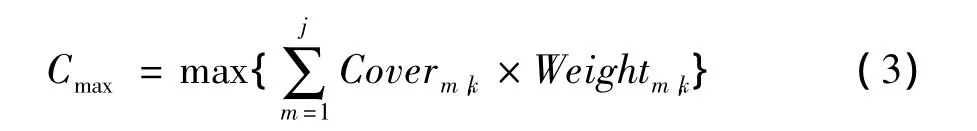
当参数值未被赋予权值时，上述两步骤中的Weightm，k=1。

4 算法描述

IPO_PW(In-Parameter-Order based Parameter Weight)算法主要是根据参数的权值对IPO中的扩展次序和参数取值进行有关改进。并且，在扩展完所有参数后，对得到的测试集用约简算法进一步处理，以获得更加简化的测试集。这种方法不仅生成的测试用例少，而且更适应现实场景对组合测试的要求。IPO_PW算法的基本步骤如下:

(1)确定待扩展参数的扩展次序:按照3．1节中待扩展参数的扩展次序的改进方法对参数进行排序。

(2)初始化，从已排序参数列中选取前2个参数，将这2个参数的所有两两组合加入测试集。

(3)重复步骤(3)～步骤(6)，直到扩展完所有参数。

(4)选取下一待扩展参数，为每个测试用例计算式(1)的值，并根据式(1)的值更新水平扩展顺序。

(5)使用水平扩展算法1进行水平扩展。

(6)使用IPO垂直扩展算法进行垂直扩展。

(7)使用算法2对扩展完后的已有测试集进行约简处理。

(8)输出测试集。

算法1水平扩展算法

输入 T={已有测试集};xj+1=待扩展参数;Dj+1={待扩展参数的取值域};Wj+1={待扩展参数的权值域}

输出 T={经过扩展后的测试集}展参数的参数取值。选取公式为:

算法2约简算法

输入 T={约简前的测试集}

输出 T’={约简后的测试集}

5 实验结果与分析

由于IPO_PW算法是在基于IPO算法的基础上实现的，因此IPO_PW算法也是一种启发式算法，它不能保证在任何情况下都能生成最小的两两组合测试集。为了检验IPO_PW算法在生成组合测试集过程中的实际效果，将IPO_PW算法的实验结果与组合测试其他几种经典算法进行比较，如表3所示。

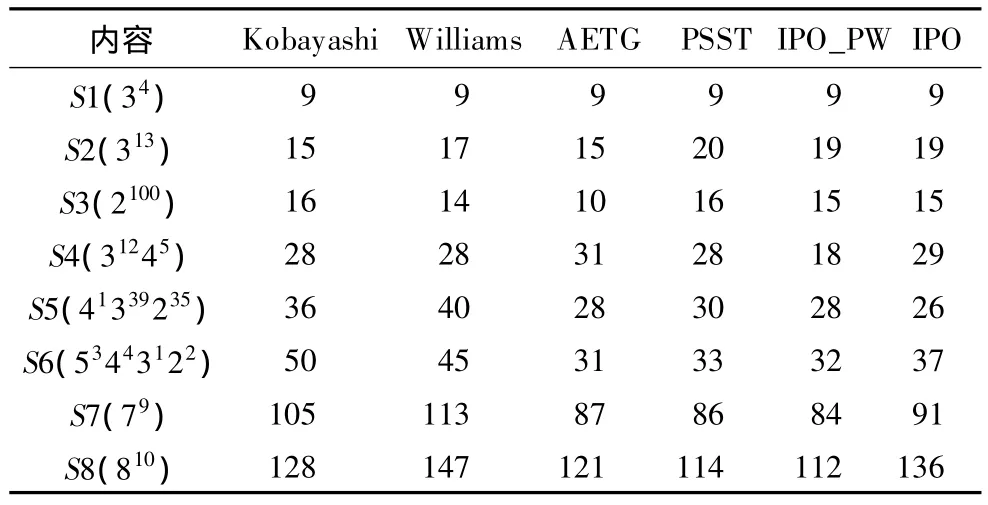
表3 6种算法的测试集大小对比

目前，有关两两组合覆盖表生成的研究主要是关注如何减小测试集规模，因此表3主要集中于各种方法生成的测试集大小的比较。从表3可以看出，IPO_PW算法总体上是可以获得较优的测试集，特别是随着测试集规模的增大，这种优越性更加明显。此外，IPO_PW算法还有一个重要特性，即它得到的测试用例是按其权值和降序排列的，在无法测试所有的测试用例时，可以优先选择那些比较重要的测试用例进行测试，这尤其适用于现实场景中。

6 结束语

本文基于IPO算法提出一种处理参数带权值的组合测试集生成算法。这种算法主要是对影响测试集的3个因素进行改进，并且在生成测试集后进行约简，进一步减小测试集的规模。实验结果表明，该算法在一定范围内不仅提高了IPO算法的测试性能，而且具有很强的实际应用性。但目前的两两组合测试算法生成的测试集都只是最优解的近似，今后将对现有算法作研究，以取得更好的测试效果。

［1］ 聂长海，徐宝文，史 亮．一种新的二水平多因素系统两两组合覆盖测试数据生成算法［J］．计算机学报，2006，29(6):841-848．

［2］ 高建华，刘 慧．配对组合测试中参数约束问题研究［J］．计算机工程与科学，2011，33(3):103-107．

［3］ Yan Jun，Zhang Jian．A Backtracking Search Tool for Constructing Combinatorial Test Suites［J］．The Journal of Systems and Software，2008，81(10):1681-1693．

［4］ Williams A W，Probert R L．A Practical Strategy for Testing Pair-wise Coverage of Network Interfaces［C］//Proceedings of the 7th International Symposium on Software Reliability Engineering．Washington D．C．，USA:IEEE Press，1997:246-254．

［5］ Noritaka K，Tatssuhio T，Tohru K．A New Method for Constructing Pair-wise Covering Designs for Software Testing［J］．Information Processing Letters，2002，81(2):85-91．

［6］ Cohen D M，DalalS R，Parelius J，etal．The Combinatorial Design Approach to Automatic Test Generation［J］．IEEE Software，1996，13(5):83-87．

［7］ Cohen D M，Dalal S R，Fredman M L，et al．The AETG System:An Approach to Test Based on Combinatorial Design［J］．IEEE Transactions on Software Engineering，1997，23(7):437-444．

［8］ 惠战伟，黄 松，苏士瀚，等．成对覆盖组合测试用例生成方法研究［C］//2010亚太地区信息论学术会议论文集．［出版地不详］:中国电子学会信息论分会，2010:264-267．

［9］ Yu Lei，Tai K C．In-parameter-order:A Test Generation Strategy for Pairwise Testing［D］．Raleigh，USA:North Carolina State University，2001．

［10］ Tai K C，Yu Lei．A TestGeneration Strategy for Pairwise Testing［J］．IEEE Transactions on Software Engineering，2002，28(1):109-111．

［11］ 严 俊，张 健．组合测试:原理与方法［J］．软件学报，2009，20(6):1393-1405．

［12］ 史 亮，聂长海，徐宝文．基于解空间树的组合测试数据生成［J］．计算机学报，2006，29(6):849-857．

［13］ 戴 丽．组合测试用例生成技术的研究与应用［D］．广州:华南理工大学，2011．