基于气象因素的SVR 方法在温州电网负荷预测中的应用
2015-01-02徐沐阳何钢健袁金腾
徐沐阳 何钢健 胡 元 袁金腾
1.温州市气象局;2.国网温州供电公司
根据温州电网的负荷特征及温州的气候特征,通过考虑气象因素优化选择历史样本数据,在预测模型中加入气象因素作为输入向量,使用回归型支持向量机方法进行温州电网的负荷预测。实践证明,考虑气象因素的回归型支持向量机方法可进一步提高温州电网负荷预测的精度。
引言
电能是现代社会必不可少的能源之一。近年来,许多研究表明电网负荷与气象因素有着密切的关系。通过分析温州电网负荷与气象因素的相关性,找到影响温州电网负荷的气象因素,并在预测算法中加以考虑。基于气象因素的回归型支持向量机方法可更好地为电力系统的安全、经济运行和优化调度等提供科学的依据。
本文根据温州电网的负荷特征及温州的气候特征,采取适用于温州电网负荷预测的计算机算法,并将之应用于实际预测工作中,取得了良好效果。
回归型支持向量机
支持向量机(SVM)是由Vapnik 等人基于统计学习理论率先提出,它的主要思想是建立一个能够使得不同分类之间的隔离边缘达到最大化的分类超平面,并以之作为决策曲面;支持向量机遵循结构风险最小化原则:学习机器在测试数据上的误差率(即泛化误差率)以训练误差和一个依赖于VC 维数的项的和为界,在可分模式情况下,支持向量机对于前一项的值为零,并且使第二项最小化;因此,在回归拟合、分类识别等问题中,支持向量机能提供很好的泛化性能,能够优于较多已有方法。支持向量机正被广泛地应用于各领域,电网负荷预测就是其中之一。
为了利用SVM 解决回归拟合方面的问题,Vapnik等人在SVM 分类的基础上引入了ε 不敏感损失函数,从而得到了回归型支持向量机(SVR)。SVM 应用于回归拟合分析时,其基本思想不再是寻找一个最优分类面使得样本最优分类,而是寻找一个最优分类面使得所有训练样本离该最优分类面的误差最小。
假设训练样本集为{(xi,y i),i=1,2,3,…,l },其中,xi(xi ∈Rd)是训练样本的输入矢量,yi 则是对应的输出数据。回归型支持向量机的公式推导过程如下:设在高维特征空间中建立的线性回归函数为

其中,φ(x) 为非线性映射函数。
定义ε 线性不敏感损失函数

其中,f(x) 为回归函数返回的预测值;y 为对应的真实值。
类似于SVM 分类情况,引入松弛变量 iξ,*iξ,并将上述ω,b 的问题用数学语言描述出来,即

其中,C 为惩罚因子,C 越大表示对训练误差大于ε的样本惩罚越大,ε 规定了回归函数的误差要求,ε 越小表示回归函数的误差越小。
求解程式(3)时,同样引入Largrange 函数,并转换为对偶形式:

其中,K (xi,xj)=φ(xi)φ(xj)为核函数。

其中,Nnsv为支持向量个数。
于是,回归函数为

从程式(7)中可以看出,SVR 最终的函数形式与SVM 相同,其结构与神经网络的结构较为类似,如图1所示。输出是中间节点的线性组合,每个中间节点对应一个支持向量。
SVR 方法在温州电网负荷预测中的应用
选择历史数据样本
根据温州本地的气候特点,分析温州历史负荷数据和气象数据,得出温州各个季节显著影响温州电力负荷的不同气象因素。显著影响春季温州电力负荷的气象因素是日最高气温和天气状况,按照预测的要求对天气状况进行量化:晴天(<1 成云)时赋值为4.多云(2~8 成云)时赋值为3,阴天(>9 成云或微量降水)时赋值为2,有雨(>0.1mm)时赋值为1;显著影响夏季温州电力负荷的气象因素是日最高气温、日最低气温和日平均相对湿度;显著影响秋季温州电力负荷的气象因素是日最低气温;显著影响冬季温州电力负荷的气象因素是日平均相对湿度。
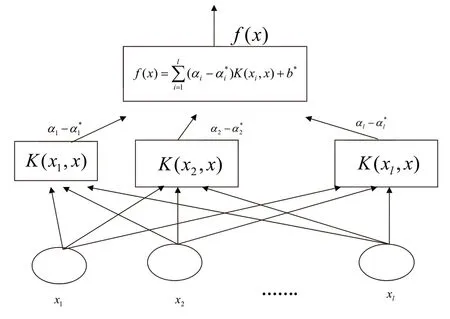
图1 SVR 的结构图
根据实际操作可行性(数据收集难易程度、数据是否连续等),在影响电网每天96 个采集点(每15 分钟一个采集点)负荷的气象因素中选取对应每天96 点的温度和湿度作为预测模型的输入向量。一天中的温度和湿度的变化是连续的,温度和湿度的日变化可以很好地表征天气日变化。但是一天中的降水的变化是不连续的,而且降水对于电网负荷的影响还具有累积效应和滞后性。况且降水的发生一定程度上也可以通过湿度的变大及持续维持高位来反应。因此,本文未选取降水量作为模型输入向量。
根据待预测日的天气条件在不同季节选取不同的具显著影响的气象因素,并以此气象因素作为依据筛选同天气类型的负荷历史数据样本,然后在其中找出与待预测日相同日类型(工作日与非工作日)的负荷历史数据样本。选定负荷历史数据样本后,再调出与其对应的气象数据样本,即对应96 点负荷数据的96 个采集点的温度、湿度数据。历史数据样本选定后,对所选的数据样本进行异常数据的判定和处理。
选择训练算法
支持向量机将需要解决的问题转化为解决一个带约束的二次规划问题,当训练样本比较少时,可以选择内点法、共轭梯度法、牛顿法等传统方法进行求解。然而,当训练样本比较大时,传统算法的复杂度会急剧增加,且占用的内存资源会很大。因此,为了减小算法的复杂度,提升算法的效率,不少专家和学者提出了许多解决大数目训练样本的支持向量机训练方法。
本文采用的是LIBSVM 算法,该算法对SVM 所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数可以解决很多问题,并且该算法还提供了交互检验的功能,提高了算法运行的速度和精度。
负荷预测的具体步骤
使用MATLAB 作为运算工具,使用回归型支持向量机方法预测待预测日负荷的具体步骤和算法流程图如下。
S1、按本文上述的历史数据样本选择规定,选定历史数据,并进行异常数据的判定和处理。
S2、将S1 中初步处理过的所有历史数据输入LIBSVM 工具箱,并选定因变量(待预测日的96 点负荷)和自变量(历史负荷、历史负荷对应的各具体气象因素),LIBSVM 将所有样本分类形成训练集和测试集。
S3、对训练集和测试集进行归一化预处理,归一化后既可以提高分类和预测的准确率,又可以方便算法的运行。

图2 程序流程图
S4、利用LIBSVM工具箱提供的功能对SVM中参数进行交叉验证以选择对于模型最优的参数(惩罚参数c、RBF 核函数中的gamma 参数g)。最佳参数c 和g 能够使得验证分类准确率达到最高,在满足条件的所有c 和g 组合中选取c 最小的那组作为模型的最佳参数。如果在满足条件的c 和g 组合中对应最小的c有多组g,那么就选取在组合序列中的第一组c 和g 作为模型的最佳参数。惩罚参数c 过大会导致支持向量机发生过学习(训练集分类准确率很高而测试集分类准确率很低),所以判定在能够使得验证分类准确率达到最高的所有c 和g 组合中较小的惩罚参数c 是更优的选择。
S5、利用S4 中选取的最佳参数,使用LIBSVM 工具箱中svmtrain 函数训练SVM,得到一个model。model 是预测模型,其中包含各种参数。
S6、利用S5 中得到的model,使用LIBSVM 工具箱中svmpredict 函数对测试集进行测试,通过预测指标来判定model 的预测性能。
S7、利用S6 中通过性能判定的model,建立决策函数
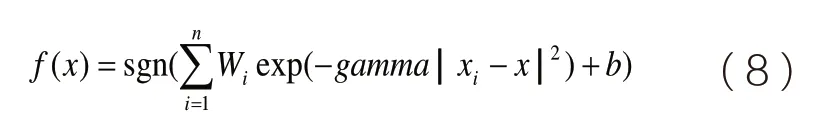
通过决策函数来预测待预测日样本的96 点负荷。其中,||xi-x||代表二范数距离;b=-model.rho(一个标量数字);n=model.totalSV 代表支持向量的个数。对于每一个表示支持向量的系数(即SVR 结构图中的);表示支持向量(历史负荷数据和各气象因子数据);x 是待预测标签的样本;gamma 就是参数g。
算法检验
假定2014 年7 月7 日(周一,工作日)的温州各县的电力负荷作为待预测日负荷,根据本文上述的历史数据样本选择规定来选取样本数据。选择与待预测日相同天气类型、日类型的参照日的数据作为历史样本数据,因此选定2014 年6 月26 日的温州各县市的负荷数据和气象数据作为历史样本数据。采用虚拟预测方法,将7 月7 日作为待预测日进行96 点的负荷预测,然后与该日的实际负荷数据作比较,以检验本文提出的日负荷预测方法的准确性和实效性。由于温州的地理位置、地形及其他一些原因,各县每天的气象条件不同、负荷数据特征不同,因此,首先进行温州各县的负荷预测,再将各县的预测负荷值累加,从而得到预测的温州地区总负荷。
如图3、4 所示:图3 为2014 年7 月7 日温州电网负荷预测的结果对比;图4 为2014 年7 月7 日温州电网负荷预测的相对误差。得出的预测结果表明:2014 年7 月7 日温州地区负荷预测准确率约为98.15%;96 个预测点中相对误差大于5%的有7 个,最大相对误差为6.49%,平均相对误差为1.27%。

图3 温州电网2014 年7 月7 日负荷预测结果对比图

图4 温州电网2014 年7 月7 日负荷预测的相对误差
依照上述算例,根据本文叙述的方法流程,对其后5个工作日(2014 年7 月8 日至7 月11 日及7 月14 日)再次进行96 点负荷预测,结果表明该5 个工作日温州地区的负荷预测准确率都达98%以上。96 个预测点中相对误差大于5%的个数依次为0、7、0、12、6;最大相对误差依次为2.29%、7.06%、1.53%、8.47%、6.08%;平均相对误差依次为0.41%、0.97%、0.02%、0.91%、0.18%。
上述算例均为一般工作日的情形,休息日、节假日的负荷预测可按同样的方法流程进行,但进行负荷预测前需对历史数据样本仔细筛选,本文限于篇幅不作赘述。具体算例可参见文献。
结语
本文采用的SVR 算法通过交互检验寻求预测模型的最优参数,加快了预测模型的运行速度与精度。通过考虑气象因素优化选择历史样本数据,在预测模型中加入气象因素作为输入向量,进一步提高了温州电网负荷预测的精度。本算例中选择了温湿条件作为气象因素输入向量,对于其他气象因素由于数据不易收集处理等原因,尚未加考虑,有待以后进一步的实践研究。
