脉冲调制信号的相位噪声恶化仿真

潘开阳

(南京电子技术研究所， 南京210039)

0 引言

相位噪声为雷达、通信及电子战等电子设备中激励信号的关键指标之一，是衡量信号质量的关键依据［1］。因此，在各种频率源系统设计中，该指标作为重要指标被考核，并且该指标的测量大多是基于连续波信号进行的。但对于脉冲体制雷达系统，发射激励信号一般都为脉冲调制信号。考虑到雷达信号脉冲重复频率远低于雷达载频信号的相位噪声频谱分布，不满足奈奎斯特采样定理，造成载频脉冲相邻谱线相位噪声的边带混叠效应，实际脉冲调制后的相位噪声较连续波信号有不同程度的恶化。特别是对于空间探测雷达和远程预警雷达，脉冲重复频率极低，使频谱混叠效应非常严重，造成雷达发射脉冲的载频相位噪声比本振的相位噪声差很多，影响雷达在强杂波环境下的高瞬时动态探测［2］。因此，需要预先量化仿真脉冲调制对连续波信号相位噪声的影响，指导雷达系统上行链路及波形调制参数设计。

本文首先介绍了连续波信号的相位噪声模型，然后详细分析了脉冲调制对连续波相位噪声的影响，最后利用SystemVue软件搭建了仿真模型对脉冲调制后相位噪声恶化程度进行量化仿真分析。

1 连续波相位噪声模型

受到内部热噪声和外界干扰的影响，频率源的输出信号不再是理想正弦波，而是相位和幅度受到噪声及干扰影响的调制信号U0，

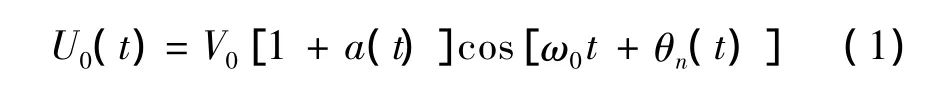
式中:V0为输出信号的幅度值;ω0为输出信号的角频率;a(t)和θn(t)分别为输出信号的相对幅值和相位的起伏;t为时间。

相位噪声在频域上的表征可以采用功率谱密度表示，通常是以单载波的幅值作为参考，然后偏移一定的频率。测量该频偏处带宽为1 Hz时的相对噪声功率，作为该信号单边带相位噪声的测量值，由于相位噪声电平低于载波信号电平，因此其为负值，可表示为

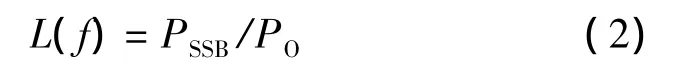
式中:PSSB为单边带偏离载波频率f时的噪声功率;PO为载波信号功率。

相位噪声的定义如图1所示。

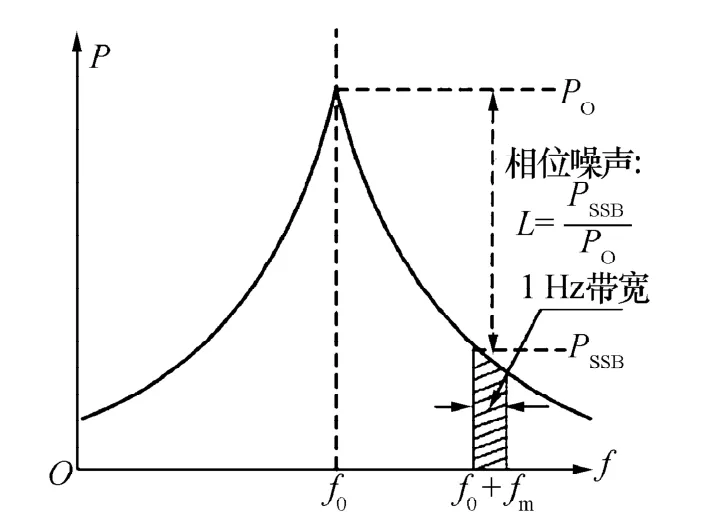
图1 相位噪声定义示意图

与通道热噪声相比，相位噪声具有以下特点:

(1)相位噪声总是伴随信号而存在的;

(2)相位噪声相比载波功率往往差几个数量级，处理的是强信号和弱噪声的问题;

(3)通道热噪声是在带宽内均匀分布的，而相位噪声功率谱密度分布满足幂律分布，不同频偏处的噪声功率谱密度相差很大，无法用平均噪声功率表征;

(4)相位噪声为乘性噪声，其恶化与载波频率有关。

2 脉冲调制对连续波相噪恶化

上面分析的相位噪声定义都是针对连续波信号而言，但对采用脉冲体制的雷达系统来说，连续波激励信号存在的相位噪声边带经过视频周期脉冲调制，调制后的信号会产生上下边带，信号的能量则包含在这些边带中［3］。

连续波信号经过脉冲调制，调制信号的上下边带谱线可以表示为

式中:FC为载波频率;n=0，1，…;PRF为脉冲重复频率。

主谱线在调制信号载波中心，旁谱线向载波中频频率两侧扩展，主谱线中最大的信号即是载波信号，组成主旁谱线幅度依据以下公式变化

式中:VC为载波中心频率幅值;VL为频偏ω处的幅值;ω为距离中心频率的频偏。

脉冲调制信号第一主瓣的宽度与调制脉冲时域宽度有关，脉冲宽度越窄，主瓣宽度越宽，第一零点位置在1/τ处。主瓣包含载波频率谱线，主瓣的宽度为 2/τ。

脉冲调制信号频谱为载波频率与脉冲信号频谱的频域卷积，如图2所示。

图2 脉冲调制信号频谱示意图

脉冲调制后的信号都会在其上下边带PRF的整数倍频偏产生响应的边带谐波信号。

如果连续波信号上存在杂散信号，脉冲调制后的信号频谱为连续波信号及其杂散信号与脉冲信号频谱的同时卷积，卷积结果为信号与杂散分别卷积结果之和［4-5］。由此可见:

(1)对含有杂散的连续波进行调制后，调制信号频谱不但包含主信号的脉冲调制，还存在杂散信号的脉冲调制，从而杂散尖峰与脉冲调制信号卷积服从函数sinX/X分布;

(2)杂散信号的脉冲调制可通过PRF折叠影响到主连续波信号中心谱线±PRF/2范围内。

连续波信号经过脉冲调制后，其中心谱线±PRF/2范围内的相位噪声受到其他PRF折叠过来的相位噪声影响，其综合效果后的相位噪声可以表示为

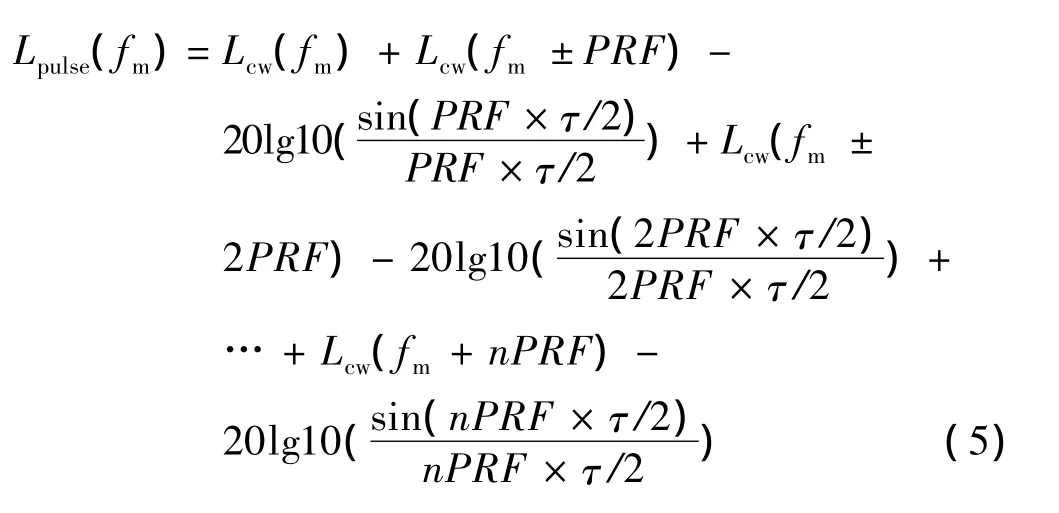
式中:Lpulse(fm)表示脉冲调制后频偏为fm的相位噪声;Lcw(fm)为连续波频偏为fm的相位噪声;PRF为脉冲重复频率;τ为调制脉冲宽度;n=1，2，…。

脉冲调制后，信号的相位噪声频谱特性如图3所示。

由图3可知:

(1)当对连续波信号进行脉冲调制时，相位噪声可视为连续杂散信号，调制后连续波信号的相位噪声会折叠到脉冲调制载波频谱的中心谱线;

(2)通过脉冲调制，偏移载波大于±PRF/2频偏相位噪声的能量可折叠到中心谱线±PRF/2频偏范围内，导致主谱线的合成噪声有所增加，脉冲调制信号的相位噪声较连续波信号的相位噪声有所恶化。

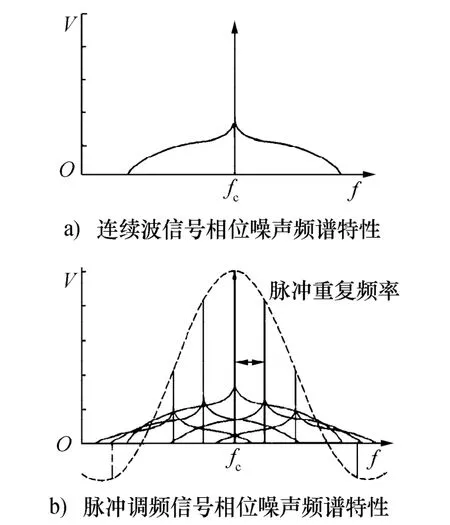
图3 脉冲调制信号相位噪声频谱图

3 仿真分析与实验验证

为了验证脉冲调制对连续波相位噪声的具体恶化程度，本文利用SystemVue软件搭建了脉冲调制相位噪声恶化仿真平台，具体模型如图4所示。

图4 仿真模型

其中仿真设置的具体参数如下:

(1)载波频率:52 kHz，功率10 dBm，相噪设置为

-76 dBc/Hz@f0±10 Hz;

-105 dBc/Hz@f0±100 Hz;

-115 dBc/Hz@f0±1 000 Hz;

-120 dBc/Hz@f0±10 000 Hz以外。

(2)信号底噪:-130 dBm/Hz。

(3)脉冲调制:周期 500 μs，脉宽 50 μs。

(4)采样率:100 kHz。

(5)频率分辨率:1 Hz。

仿真结果如图5所示。由图5可知:

(1)脉冲调制后，近端相位噪声恶化程度较小，如80 Hz频偏处的相噪恶化只有0.5 dB，230 Hz频偏的相噪恶化达5.7 dB;

(2)远端相位噪声恶化程度基本平稳，1 kHz频偏外的相噪恶化为9.7 dB。

图5 仿真模型

通过更改仿真参数，如脉冲调制周期、脉宽，连续波基底热噪声，重新仿真对比后可以得到:

(1)脉冲调制后的相位噪声是在连续波基础上恶化的，近端(1 Hz～100 Hz)由于相噪基底较高，对脉冲调制混叠效应引入的相噪恶化不敏感，中端(100 Hz～200 Hz)有一定程度恶化，远端(大于200 Hz)恶化程度较大;

(2)脉冲调制后相位噪声在近端频偏处的恶化程度与脉冲周期、脉宽、连续波相噪分布、基底热噪声等因素有关，脉宽减小或周期增大时，频谱混叠程度增强，相噪恶化增大;

(3)当基底热噪声小于相位噪声1个数量级以上时，脉冲调制后远端频偏处的相位噪声恶化可用公式10lg10(1/占空比)来量化表达;

(4)当连续波信号的基底热噪声与相噪水平相当时，基底热噪声开始影响脉冲调制后的相噪指标测试，因此设计频率源时需尽量采用低噪声模拟器件，合理设计上行链路增益分布，减少附加热噪声对相位噪声的影响;

(5)注意连续波信号PRF以外的杂散，可通过脉冲调制折叠进入主频谱±0.5 PRF中，影响脉冲调制信号相噪测试结果。

为了验证仿真的可行性，利用信号源和频谱仪搭建实验平台进行实验验证。其中，信号源采用安捷伦公司的E8257D，产生1.1 GHz连续波信号，采用周期500 μs，脉宽 50 μs进行脉冲调制;频谱仪采用安捷伦公司的E4440B。连续波和脉冲调制后的相位噪声测试结果见表1。

表1 连续波和脉冲调制相位噪声测试对比

可以发现，连续波形信号经过脉冲调制后，近端频偏(1 Hz～100 Hz)恶化较小，为3.4 dB左右，但是远端(大于230 Hz)频偏恶化较大，为6.2 dB～10.9 dB，测量数值基本与前面仿真结果一致，验证了仿真方式的有效性和结论的可行性。

4 结束语

针对脉冲调制后相位噪声的混叠效应，本文利用SystemVue软件搭建了脉冲调制对连续波相位噪声影响的仿真模型，通过仿真可以看出:脉冲调制信号的相位噪声是在连续波基础上恶化的，近端频偏由于相噪基底较高，对脉冲调制混叠效应引入的相噪恶化不敏感，中端频偏有一定程度恶化，远端频偏恶化程度较大;相位噪声的具体恶化程度与频偏位置、脉冲周期、脉冲宽度及基底热噪声等因素有关，这对采用脉冲调制体制雷达系统的相位噪声测量具有实际参考意义。

［1］ 施 柳，杨 芳，李海松.基于直接频谱法的相位噪声测试方法研究［J］.上海航天，2012，29(3):69-72.Shi Liu，Yang Fang，Li Haisong.Research on testing method of phase-noise based on direct spectrum analysis method［J］.Aerospace Shanghai，2012，29(3):69-72.

［2］ 郭崇贤.相控阵雷达接收技术［M］.北京:国防工业出版社，2009:210-212.Guo Chongxian.Receiving technology of phased-array radar［M］.Beijing:National Defense Industry Press，2009:210-212.

［3］ 张贵军，周 渭，郑延秋.脉冲调制对连续波载波单边带相位噪声的影响［J］.宇航计测技术，2003，23(1):17-20.Zhang Guijun，Zhou Wei，Zheng Yanqiu.Affection to phase noise of a CW carrier by the pulse modulation［J］.Journal of Astronautic Metrology and Measurement，2003，23(1):17-20.

［4］ 张志鑫，颜 雨.相位噪声对多普勒雷达接收机影响的分析［J］.成都电子机械高等专科学校学报，2012，15(1):25-27.Zhang Zhixin，Yan Yu.Analysis of phase noise effects on Doppler radar receiver［J］.Journal of Chengdu Electromechanical College，2012，15(1):25-27.

［5］ 陈晓龙，王家礼，孙 璐，等.脉冲调制信号相位噪声测量中的功率谱估计方法［J］.西安电子科技大学学报，2012，39(4):138-143.Chen Xiaolong，Wang Jiali，Sun Lu，et al.Method for estimating power spectral density in pulsed carrier phase noise measurements［J］.Journal of Xidian University，2012，39(4):138-143.