基于BM窗口竞争的高效单模式匹配算法

陈 伟，滕宏舜

（浙江师范大学数理与信息工程学院，浙江 金华321004）

1 概述

字符串模式匹配，即在一个文本T＝t1t2…tn中找出某个特定模式串P＝p1p2…pn首次出现或所有模式串出现的位置，其中，T和P都是有限字符集Z上的字符序列；n和m 为正整数，且n≥m。T中当前和模式P进行匹配的m长子串被称为匹配窗口。

字符串模式匹配算法作为基础算法之一，已被广泛应用于计算机和网络数据搜索方面。它在文档编辑、文献资料检索、海量数据挖掘、DNA序列检测、病毒检测、图像处理、Web搜索、网络入侵检测、内容安全技术及事务管理系统等非数值处理方面有非常广泛的应用。如网络入侵检测系统，约有30%的时间用来进行模式匹配［1］，而在加强网络交互的情况下，则用于模式匹配的时间约占总量的80%［2］。

模式匹配问题可分为单模式匹配和多模式匹配2类。典型的单模式算法主要有KMP算法、SKIP算法、BM算法［3］。其中有大量基于BM的改进算法 BMH［4］，BMHS［5］，BMH2C［6］，BMG［7］更适合中文字符的 BM 改进［8］、N－BMHS［9］。文献［10］分析双字符串在模式串中出现的不同情形和模式串后继字符的关系确定右移量。文献［11］提出基于Sunday算法的改进算法，在匹配前先找到模式串中的特征字符（出现概率最小的字符），再进行特征字符与尾字符双重匹配，增大了首次不匹配的可能性。文献［12］提出Sunday改进算法，利用Unicode中文双字节编码的内部关联性，优化原Sunday算法的跳转值，补偿Sunday算法因降低空间消耗而造成的时间效能损耗，提升在中文Unicode编码环境下的匹配性能。Y＿BMHS算法［13］利用辅助的二维数组，文本串中间隔的2位字符和模式串首字符的唯一性，使得模式串以最大位移m＋3进行右移的概率提高。

本文以经典单模式匹配算法Boyer－Moore（BM）为研究对象，充分利用BM系列改进算法之间的差异性实现失配窗口右移距离最大化，以窗口竞争的思想提高匹配窗口到位率，尽量减少不必要的匹配过程。

2 BM算法及其改进算法

BM系列算法的特点是从模式串P的尾部（最右端）开始扫描。它将P与目标文本T的左端对齐后，在匹配窗口中自右向左逐个比对。

2．1 BM 算法

BM算法采用坏字符和好后缀2项规则。设Z为与P，T相关的有限一元字符集，P中的字符构成Z的子集Zp，k为当前模式匹配窗口尾部所在位置，即窗口的最右端。坏字符规则使用预计算的skip数组，定义为：

在该规则中，一旦某字符失配，即P［i］≠T［j］，则跳跃距离s＝skip1（x）－（m－i），如图1所示。

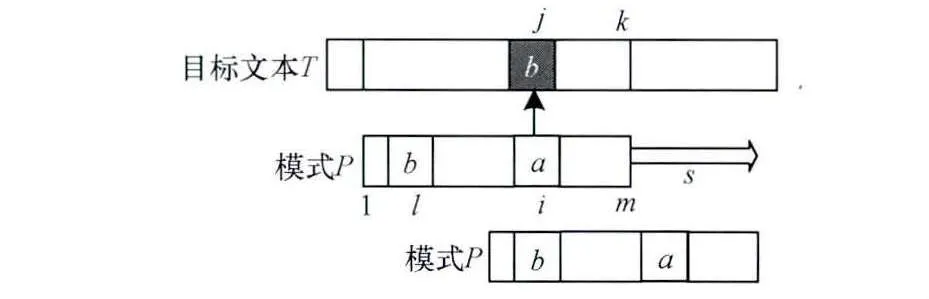
图1 坏字符规则

好后缀规则使用预计算的shift数组。在该规则中，如果P尾部的k位（记为P1子串）已经和当前匹配窗口中T的部分字符串（记为T1子串）匹配成功（P1＝T1），此时的下一位字符却突然发生失配，则算法检查P中前边m－k位是否存在该P1子串的同版本子串P2（P2＝P1）。若P2存在，则将模式串P右移使P2与T1对齐。否则，检查P从最左边字符开始的m－k位中是否存在前缀P3，使之成为P1的任意后缀。如果存在，则右移模式串使其对齐。如果两者皆不存在，此时可直接将模式串P向右移动，使P［1］对齐T1后的第一个字符。

BM算法的预处理时间复杂度为O（m＋Z），空间复杂度为O（Z），最好情况下的时间复杂度为O（n／m），最坏情况下时间复杂度为O（nm）。

2．2 BM系列改进算法

BM的内在缺陷在于：坏字符规则可能造成右移数为负值（回头左移）。所以，算法取2个规则函数所产生移动值中更大的那个数为右移距离。

另一个问题是：好后缀规则的实用性不强。好后缀规则的预处理和计算过程都较复杂。而且，研究表明，坏字符规则在匹配过程中占主导地位的概率为94．03%，远远高于好后缀。因此，文献［4］提出的BMH算法以及后续类似改进都抛弃了好后缀，而只采用坏字符规则。

BMH解决了BM算法中模式串有可能左移的问题。在BMH中，无论失配发生在当前窗口的什么位置，都由目标文本T中和模式串最后一个位置pm对应的字符tk，即当前窗口的尾字符来决定右移距离。它比BM更紧凑，效率也更高，在最好的情况下复杂度为O（n／m）。

文献［5］将BMH进一步改进成了BMHS，其主要思想是：利用当前窗口的下一个字符tk＋1而不是尾字符tk来计算右移量，即将skip函数改为：

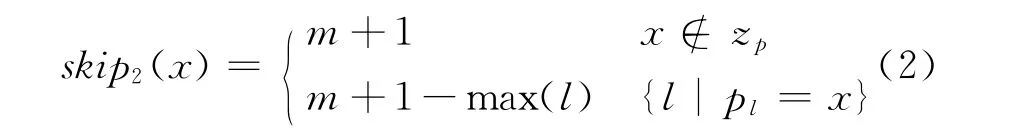
这使得最大和平均移动距离分别由m和（m＋1）／2增加为m＋1和（m＋1）／2。BMHS在最好情况下的时间复杂度为O（n／m＋1）。通常情况下，其速度大于BMH。

但是，BMHS相对于BMH有一个缺陷：当tk＋1出现在模式中，而tk不出现时，BMHS的右移距离反而不如BMH，使其匹配窗口反而落后于BMH。

一些研究者注意到两者间的差异性。文献［6］提出了BMH2C算法，用当前窗口末字符tk和下一字符tk＋1组成二元组来计算右移量。设Z2为基于字符集Z的二元字符集，Z2P为P中二元字符组集合。文献［6］重新定义了skip函数：

上述3种算法的右移量比较如表1所示。

表1 3种算法的右移量比较

从表1可见，BMH2C克服了BMH和BMHS的缺点，达到了后两者的最优解。但另一方面，BMH2C只是对它们的合并和微调，其最大右移量仍然是m＋1，并未获得突破性改进。

2．3 BMG算法

文献［7］的研究同样基于BMH和BMHS。当BMHS窗口落后于BMH时，其匹配过程是多余的。希望对BMHS进行改进，使其窗口能进一步向右滑动，提出的方法是定义一个唯一性函数：

然后，据此考察tk＋1字符在模式P中出现的唯一性。由此，提出了BMG算法。算法过程为：（1）计算出由字符tk得到的右移位置k1＝k＋skip1（tk）（原BMH部分）和由字符tk＋1得到的右移位置k2＝k＋skip2（tk＋1）（原 BMHS部分）。（2）判断两者的大小。如果k1＞k2，再判断tk＋1在模式串中出现的频次。若 Q（tk＋1）＝1，则将tk＋1＋m和模式串末端对齐作为新匹配窗口（BMHS改进部分）；否则，便意味着即使经过这样的改进，BMHS窗口依然跟不上BMH，只能放弃该窗口，将tk1和模式串末端对齐。

可以看出，唯一性函数Q（x）对BHMS算法的落后只是部分补偿，该算法有一定的改进效果，提供了一种无需进行任何字符比对便能确定当前窗口是否失配的前景。但对BMH和BMHS的设计思想仍然是突而不破，仅考虑了k1＞k2时的情形。其最大右移距离仍是m＋1。它存在2大问题：

（1）当落后的BMHS窗口获得补偿超越靠前的BMH窗口，使之成为新的落后窗口时，未有效利用该新落后窗口信息，只是将之简单地抛弃。

（2）没有利用落后BMHS窗口的尾字符信息，浪费了获取更大跳跃距离的可能性。

3 窗口竞争技术

3．1 窗口滑动过程

从第2节可以看出，对BMH，BMHS的改进成为模式匹配算法进化的主要途径之一。一种最简单的改进方式为：对于skip（tk）＝m，通过连续测试找到满足skip（tk＋lm）≠m（l∈N＋）的最小l值，以此定位窗口位置。对于skip（tk＋1）＝m，亦可作类似处理。

从表1可以看出，BMH，BMHS和BMH2C3种算法的右移步伐是不一样的。设它们自同一匹配窗口起步后，右移距离从小到大依次排列为a，b，c，即有a≥b≥c，如图2所示。此时，若有a＝b＝c，说明3种算法达成一致，可以开始在窗口字符与模式串之间进行比对，判断是否能找到一个匹配。否则，必有至少一个窗口的右移距离最大，处于最右的位置，被称为前端窗口，而其余窗口则落在后面，被称为落后窗口。可以认为落后窗口无需比对即告失配。此时，如何处理它们成为关键问题。

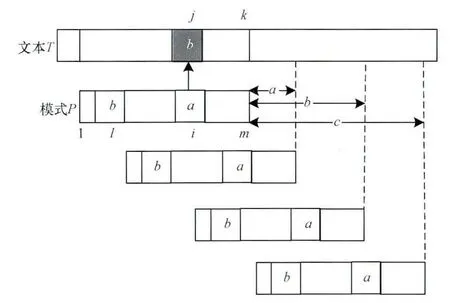
图2 3种算法的不同步右移

如同BMG和其他类似改进所期望的那样，每个落后窗口的使命都是尽快超越当前的前端窗口，使之与自己地位对换。如此反复，便可以在不进行任何字符比对尝试的情况下，仅通过计算skip函数就使窗口不断向前滑动，从而大大减小比对次数。

为达上述目的，落后窗口应尽量使用右移距离最大的BMH2C实现超越（即测试tktk＋1的skip3函数），并且需要维护一张按位置前后排序的窗口状态表。

3．2 BMHS2C

结合BMHS和BMH2C算法，利用模式串对应文本串末尾后面2个字符串tk＋1tk＋2来计算右移量，使得文本串的右移量最大提升到m＋2。skip函数如下：

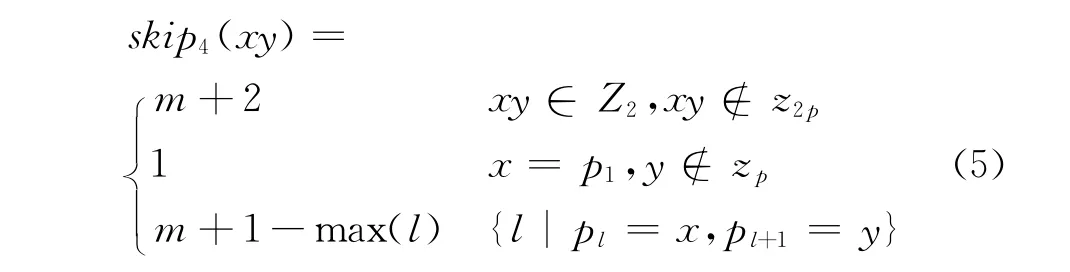
3．3 Q（x）函数

为使每个落后窗口都能产生尽可能大的右移量，引入文献［7］中定义的唯一性函数Q（x），并将其扩展到二元字符组上，定义类似函数如下：

因此，每次落后窗口右移时，如果skip1（tk）＜m 但Q（tk）＝1，则视同skip1（tk）＝m。类似的，如果skip2（tk＋1）＜m＋1 但 Q（tk＋1）＝1，则 视 同skip2（tk＋1）＝m＋1。如果skip3（tktk＋1）＜m＋1但Q2（tktk＋1）＝1，则视同skip3（tktk＋1）＝m＋1。

显然，当落后窗口虽努力右移仍无法超越当前的前端窗口时，则消亡。一旦落后窗口消化殆尽，一个新的匹配窗口便自然产生，此时便可以开始字符逐个比对的匹配过程。当匹配窗口发生失配时，则需要使用3种算法进行窗口衍生。

4 算法使用数据及处理过程

本文充分利用BM改进算法之间的差异性达到右移距离最大化，考虑特征字符tk＋1在模式串P中出现的次数，以及窗口竞争思想，使匹配窗口到位率大大提高，尽量减少不必要的匹配过程。

4．1 数据项

根据上节描述，算法需要使用如下数据：

（1）长为m的模式P的匹配序数组；

（2）长为3的窗口状态数组State，其值为：2＝当前窗口，1＝落后窗口，0＝作废窗口；

（3）长为3的窗口尾部位置数组k，分别代表BMH，BMHS和BMH2C算法计算得到的窗口位置；

（4）标识当前窗口属于哪个算法的变量up；

4．2 预处理

预处理步骤如下：

（1）初始化各个数组；

（2）扫描模式串，按式（1）～式（3）分别建立skip函数数据项，按式（4）、式（5）分别建立Q 和Q2数据项。

上述预处理步骤的复杂度为O（Z＋Z2），稍高于BM的预处理复杂度O（Z＋m）。

4．3 算法流程

算法流程及匹配过程如图3～图7所示。在以上实例中，对I＿BMH2C和Skii－BM算法的匹配过程进行了对比。利用BMH和BMHS2C进行窗口竞争，在第2轮中BMH的窗口超过了BMHS2C，则跳过字符匹配，BMHS2C直接进行下一轮右移。

图3 Skii－BM算法总体流程

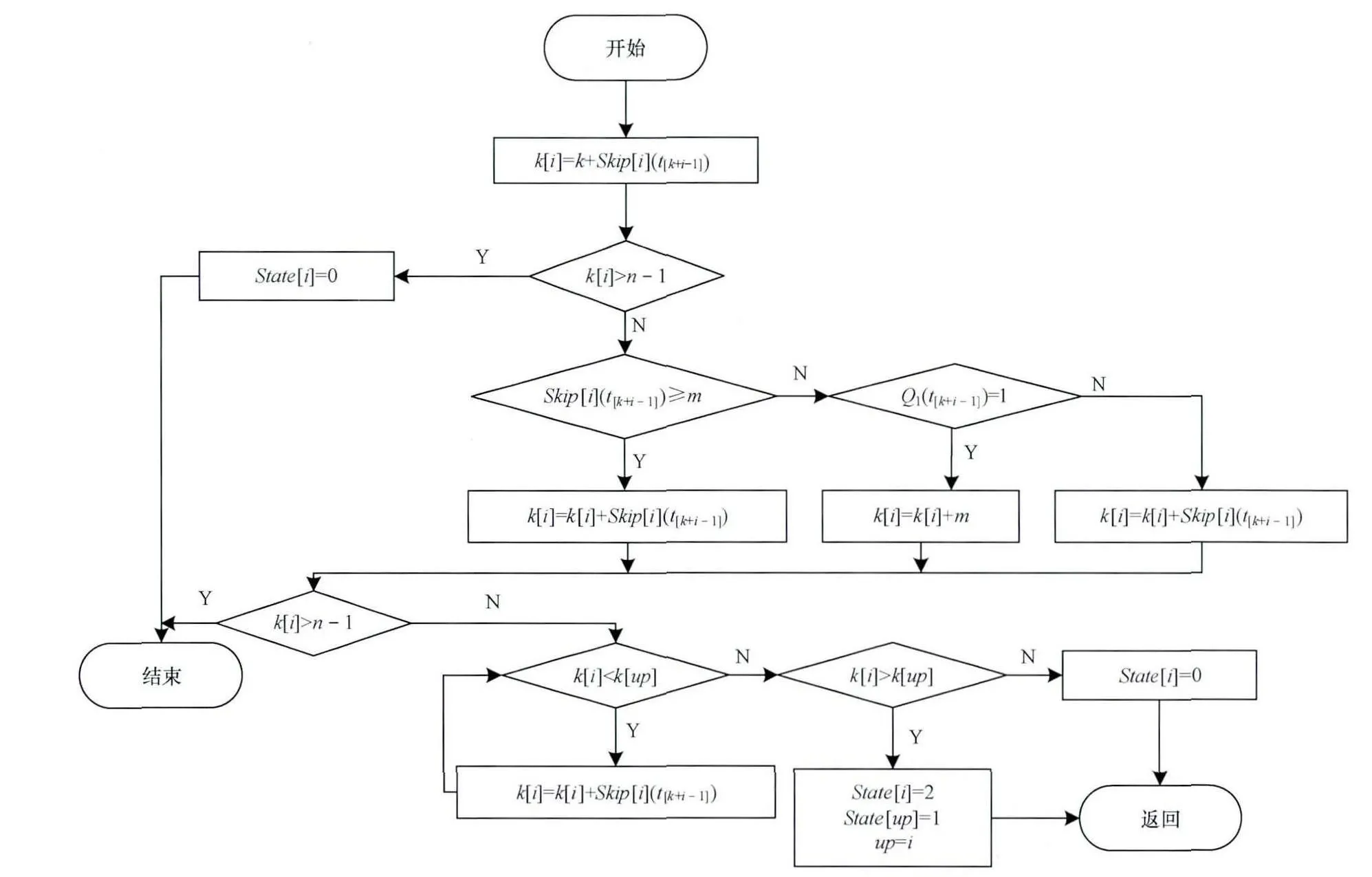
图4 BMH和BMHS窗口滑动流程

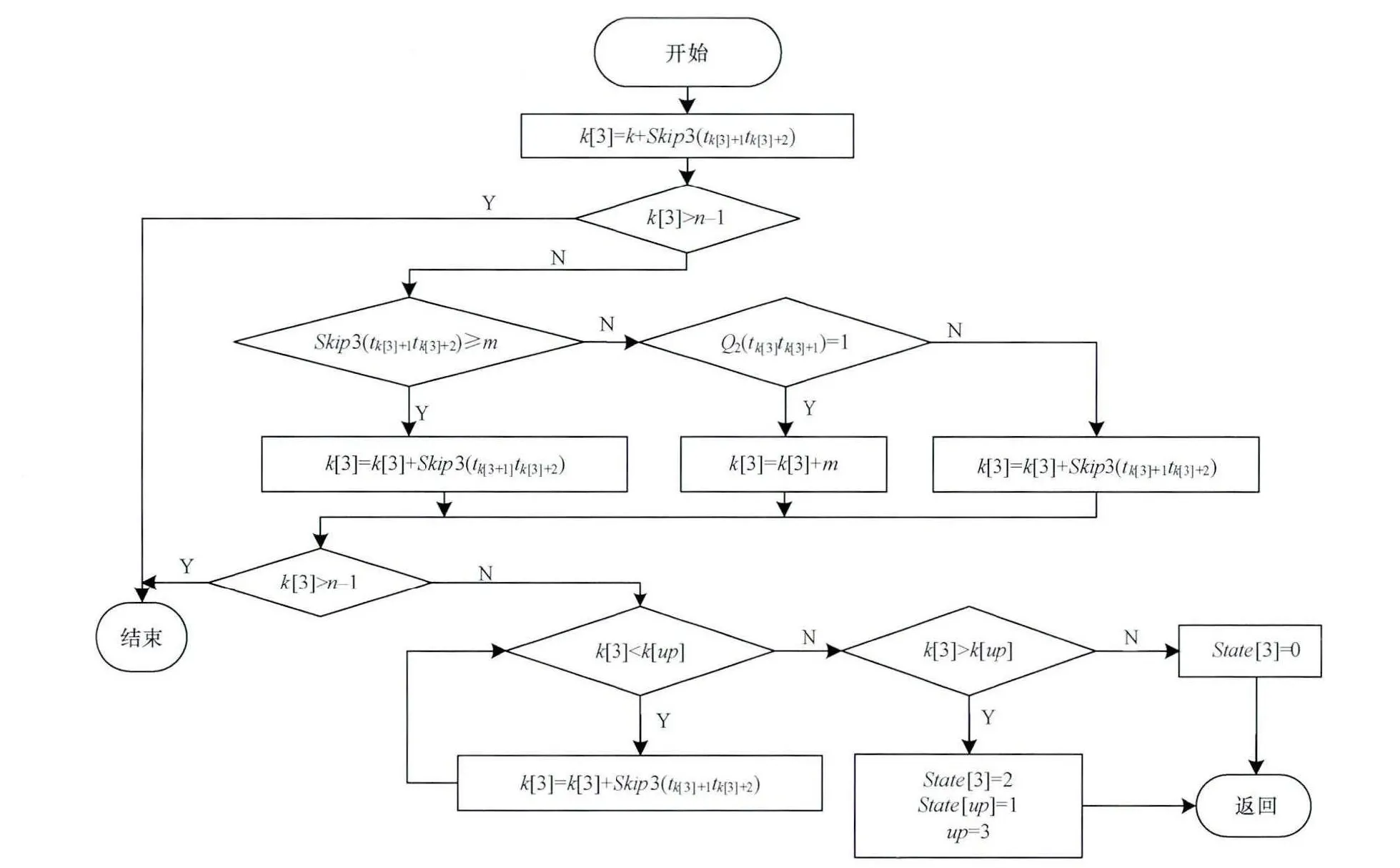
图5 BMH2C窗口滑动流程

图6 I＿BMH2C算法匹配过程

图7 Skii－BM算法匹配过程

5 实验结果与分析

在Windows XP操作平台，CPU酷睿双核T6600，主频2．2GHz，内存2GB，主频1 067MHz的环境下，选择200KB大小的英文语料重复500次对BMH，BMHS，BMH2C和Skii－BM 4种算法进行测试。为增强准确性，选取了模式长度分别为10以下和10以上的2组模式进行比较。窗口竞争对比实验数据如表2和表3所示。

表2 模式长度小于10时的窗口竞争实验数据

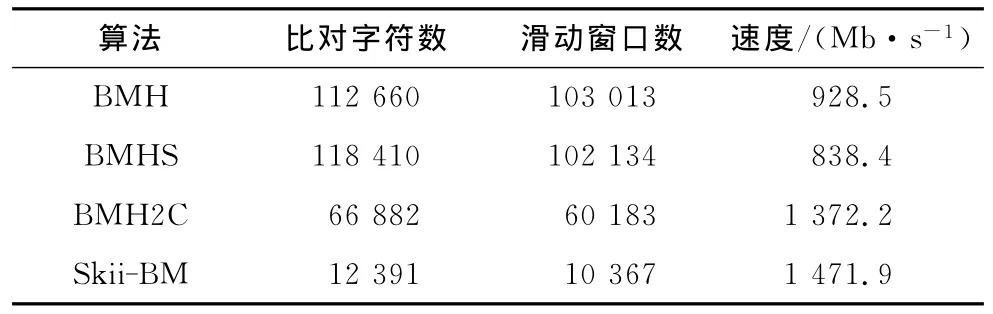
表3 模式长度大于10时的窗口竞争实验数据

由上述实验可以看出，Skii－BM算法在比对字符数和窗口滑动数较BMH，BMHS，BMH2C算法减少明显，匹配效率大幅提高。其中，当模式串长度小于10时，由于tk，tk＋1所组成的双字符组出现在模式串P中的概率较小，则BMH2C的右移量为m＋1的概率较大。窗口竞争的思维也主要以BMHS2C的右移量为主。在字符比对数和窗口滑动数方面优势明显，由于处理阶段的额外开销高于BMH2C，因此利用Q函数和窗口竞争的Skii－BM算法速度有所下降。但在处理长模式时，其优势更明显。

6 结束语

目前对于BM算法的改进算法有很多，在对不同文本模式进行匹配时也有各自的优势。本文在对已有的BM算法研究基础上提出改进算法，即Skii－BM算法。实验数据证明，与以往改进算法相比，该算法的速度和效率都有较大改善，在模式匹配算法的应用领域中具有更好的性能。

［1］Fisk M，Varghese G．An Analysis of Fast String Matching Applied to Content－based Forwarding and Intrusion Detection，CS2001－0670［R］．San Diego，USA：University of California，2002．

［2］Antonatos S，Anagnostakis K G，Markatos E P．Generating Realistic Workloads for Network Intrusion Detection Systems［C］／／Proceedings of ACM Workshop on Software and Performance．New York，USA：ACM Press，2004：207－215．

［3］Boyer R S，Moore J S．A Fast String Searching Algorithm［J］．Communications of the ACM，1977，20（10）：762－772．

［4］Horspool N．Practical Fast Searching in Strings［J］．Software Practice and Experience，1980，20（10）：501－506．

［5］Sunday D M．A Very Fast Substring Search Algorithm［J］．Communications of the ACM，1990，33（3）：132－142．

［6］钱 屹，侯义斌．一种快速的字符串匹配算法［J］．小型微型计算机系统，2004，25（3）：400－413．

［7］张 娜，侯整风．一种快速的BM 模式匹配改进算法［J］．合肥工业大学学报：自然科学版，2006，29（7）：834－838．

［8］刘沛騫，冯晶晶．一种改进的BM模式匹配算法［J］．计算机工程，2011，37（17）：248－250．

［9］单懿慧，蒋玉明，田诗源．面向入侵检测的改进BMHS模式匹配算法［J］．计算机工程，2009，35（24）：170－173．

［10］王艳霞，江艳霞．BMH2C单模匹配算法的研究与改进［J］．计算机工程，2014，40（3）：299－301．

［11］万晓榆．改进的Sunday模式匹配算法［J］，计算机工程，2009，35（7）：125－129．

［12］朱永强．基于Sunday算法的改良单模式匹配算法［J］．计算机应用，2014，34（1）：208－214．

［13］杨子江．一种快速的单模式匹配算法［J］．华南师范大学学报：自然科学版，2013，45（5）：32－35．