MAC算法计算二维方腔顶盖流动

李江飞，石兆东，段兴华，李岩芳，张　康，逯国强，陈颖超，任亚东（承德石油高等专科学校热能工程系，河北承德067000）

MAC算法计算二维方腔顶盖流动

李江飞，石兆东，段兴华，李岩芳，张康，逯国强，陈颖超，任亚东
（承德石油高等专科学校热能工程系，河北承德067000）

二维方腔流动是不可压缩黏性的典型流动，可以用来检验各种数值算法计算精度和可靠性，目前尚不能求得它的解析解.基于Matlab编程，采用交错网格MAC算法求解二维方腔流动，计算采用控制容积积分法离散控制方程，对流项和扩散项采用中心差分格式，得到流动达到稳定状态时各物理量的分布.

数值模拟；方腔流动；控制容积积分法；MAC算法；离散

Li JF,ShiZD,Duan XH,etal.Calculation of Two-dimensionalCavity Flow Based on MAC[J].Journal of Yibin Univer⁃sity,2015,15（6）：28-31.

二维不可压缩黏性流体方腔流动顶盖拖动速度为utop，方腔的长度和高度均为H,流体密度为ρ、动力粘度为 μ.边界条件：流动速度u、v采用无滑移边界条件，利用动量方程推导压力p的边界条件[1].

流动与传热的控制方程如下：

其中，p为压力，u、v分别为x、y方向速度分量.用高度H、流体密度ρ和拖动速度utop作为无量纲标尺，将控制方程无量纲化，流场初始状态为静止，R e=1000求流动达到稳定状态时，x方向中垂线（x=H/2）上的无量纲速度U，y方向中垂线（y=H/2）上的无量纲速度V，绘制出速度分布曲线，并求出中垂线上||U、||V的平均值.

1　问题分析

1.1涡量控制方程无量纲化

以高度H、流体密度ρ和速度utop作为无量纲标尺，将控制方程无量纲化[2]：

将上述无量纲量代入题中流动与传热的控制方程，得出如下的无量纲方程：

1.2边界条件

边界条件为：流动速度采用无滑移边界条件，壁面处法向速度恒为0，切向速度也为零.顶盖u=1，v=0；其余u=v=0.

2　网格划分

采用均分网格，网格数80×80的交错网格来离散方程，将压力和速度放在不同位置，压力放在网格中心，以Pi,j为主节点，背离P点的U、V与P点有相同的编号，速度分量U与P在X方向位置相错半个网格，速度分量V与P在Y方向位置相错半个网格，具体如下[3]：

P：

X方向：0—81，左边点0，右边点81，边点与内点距离为，其余ΔX；Y方向：0—81，下边点0，上边点81，边点与内点距离，其余ΔY；

U：

X方向：0—80，左边点0，右边点80，相邻两点距离ΔX；Y方向：0—81，下边点0，上边点81，边点与内点距离，其余ΔY；

V：

3　离散方程

对于MAC算法而言，采用交错网格，用控制容积积分法离散控制方程，对流项和扩散项采用中心差分格式.时间步长为Δτ，空间步长为ΔX、ΔY.

对速度分量U进行离散[4-5]：

内点处理：

非稳态项：

对流项：

扩散项：

压力项：

边界点处理：

对于上边界点，扩散项：

对于下边界点，扩散项：

内点离散后的动量方程为：

对速度分量V进行离散：

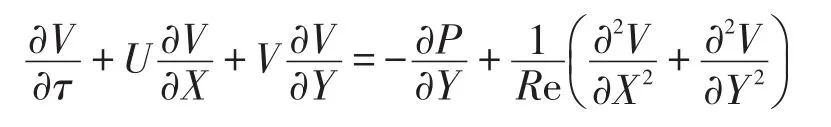
内点处理：

非稳态项：

对流项：

扩散项：

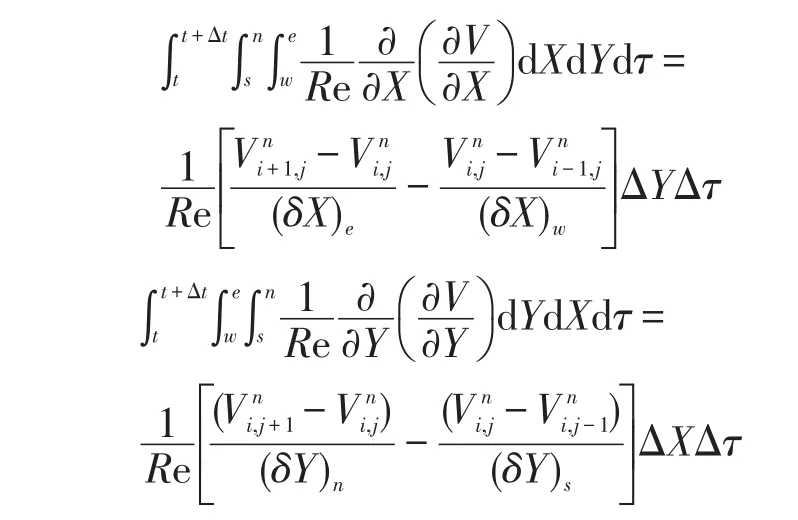
压力项：

对于左边界点，其扩散项：

对于右边界点，其扩散项：

离散后的动量方程为：

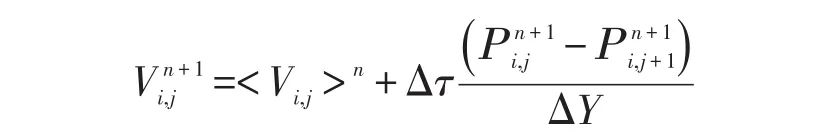
整理化简可得压力离散方程：

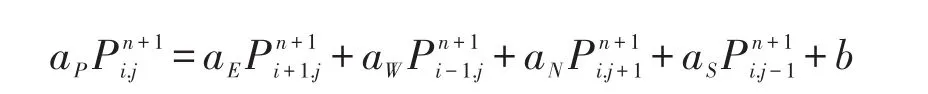
其中：aP=aE+aW+aN+aS,aE=aW=aN=

4　求解方法

求解步骤如下[6-8]：

①确定网格信息，如空间步长、时间步长：ΔX，ΔY，Δτ；②定义变量，给速度场和压力场赋初始值和边界值；③经过（1）、（2），可得完整的速度场离散结果，据公式求；④根据（3）求解压力泊松方程，采用Gauss-Seidel迭代求解，循环直至满足收敛条件；⑤用该时层满足收敛条件最新的压力场去更新速度场，得到下一时层的，；⑥用下一时层的，返回（4），直到稳态的解，求出速度场和压力场.程序流程如图1所示.

图1　求解程序框图

5　结果与结论

图2　方腔压力场分布图（N=80；R e=400；t=0.0005,0.001,0.002,0.005,0.01）

图3　方腔中心速度分布比较图（N=20,40,80；R e=1000）

[1]Peng Y F,Shiau Y H,Hwang R R.Transtion in a 2-D lid-driven cavity flow[J].Computer＆Fluids,2003,32（3）：337-352.

[2]陶文铨.数值传热学[M].第二版.西安：西安交通大学出版社，2010.

[3]Abdallah S.Numerical solutions for the pressure poisson equation with neumann boundary conditions using a non-staggered grid[J].Journalofcomputationalphysics,1987,70（1）：182-192.

[4]Hortmann M,PerićM,ScheuererG.Finite volumemultigrid predic⁃tion of laminar natural convection：Bench-mark solutions[J].Inter⁃national Journal for Numerical Methods in Fluids,1990,11（2）：189-207.

[5]DemirdžićI,PerićM.Finite volumemethod for prediction of fluid flow in arbitrarily shaped domainswithmoving boundaries[J].Inter⁃national Journal for Numerical Methods in Fluids,1990,10（7）：771-790.

[6]Brandt A.Multi-level adaptive technique（MLAT）for fast numeri⁃cal solution to boundary value problems[C].Proceedings of the Third International Conference on NumericalMethods in Fluid Me⁃chanics,Springer Berlin/Heidelberg,1973：82-89.

[7]Wang J,Li JF,ChengW X,et al.Comparison of finite difference and finite volume method for numerical simulation of the incom⁃pressible viscous driven cavity flow[J].Advanced Materials Re⁃search,2013（732-733）：413-416.

[8]Li JF,Long J,Yuan L A,etal.Comparison of finite difference and finite volumemethod for numerical simulation of driven cavity flow based on MAC[C].Computational and Information Sciences（IC⁃CIS）,2013 Fifth International Conference on,Shiyang,2013：891-894.

（编校：许洁）

Calculation of Tw o-dimensionalCavity Flow Based on MAC

LIJiangfei,SHIZhaodong,DUAN Xinghua,LIYanfang,ZHANG Kang,LUGuoqiang,CHEN Yingchao,REN Yadong
（DepartmentofThermalEngineering,ChengdePetroleum College,Chengde,Hebei067000,China）

Two-dimensional square cavity flow is a typical incompressible viscous flow,which can be used to testa vari⁃ety ofnumericalalgorithms for computationalaccuracy and reliability,yet itsanalytical solution still cannotbe achieved.Based on Matlab programming,the staggered grid MAC algorithm was used to solve two-dimensional square cavity flow.Control volume integralmethod was used to discrete the control equations for calculation.Central difference scheme was applied for convection and diffusion terms.In the end,the flow simulation resultsofeach physicalquantity distribution in steady statewere obtained.

numericalsimulation；cavity flow；controlvolumemethod；MAC；discrete

TB126

A

1671-5365（2015）06-0028-04

2015-04-12修回：2015-04-17

李江飞（1988-），男，讲师，硕士，研究方向为油气储运

网络出版时间：2015-04-21 20：46网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20150421.2046.001.html

引用格式：李江飞，石兆东，段兴华，等.MAC算法计算二维方腔顶盖流动[J].宜宾学院学报,2015,15（6）：28-31.