基于Dempster-Shafer理论的GHSOM入侵检测方法

苏洁，董伟伟，许璇，刘帅，谢立鹏

（哈尔滨理工大学 计算机科学与技术学院，黑龙江 哈尔滨 150080）

1 引言

入侵检测系统可以采集网络节点中流量数据，对传输行为实时检测，分析并发现是否有正在入侵的行为或已经发生的入侵行为，对发现的可疑传输向管理员发出警报或者自身采取主动反应措施，由此可见，这是信息安全防御系统的另一道防线，是系统安全的重要组成部分之一。目前开展研究的入侵检测算法和模型主要有基于数据挖掘、基于人工免疫、基于神经网络等类型[1,2]。

入侵检测技术的一个重要发展方向是基于神经网络的入侵检测方法。神经网络算法具有自适应、自组织、泛化能力以及高度并行性和非线性映射等优点，在环境多变且状况频发的网络入侵检测中有很大的应用前景。随着近些年对其研究的不断深入，基于无监督生长型分层的自组织映射神经网络（GHSOM, growing hierarchical self-organizing maps）模型的入侵检测研究越来越得到关注[3,4]。Zell等[5]将神经元分布在球体表面上，提出了自组织表面（SOS, self-organizing surfaces）算法，通过动态地在大概率获选的神经元周围增加神经元的方法，完成对网络规模和稀疏的动态表述。Deng等[6]根据高速处理数据的需要在学习过程中增加神经元，并对输入样本调整神经元的权值，提出了演化SOM（ESOM, evolve self -organizing map）算法。杨雅辉等[7]基于对检测过程中的新型攻击进行增量式学习，动态地对模型本身进行扩展，提出了增量式GHSOM神经网络的方法。

针对网络数据的不确定性中的随机性和模糊性的问题，同时考虑到对子网拓展规模的动态控制，将DS证据推理理论引入其中。DS证据推理理论在不确定信息表示方面不仅可以将经验性、条件性信息进行融合，而且随机信息、模糊信息也能通过不同的手段转换到证据理论的框架下进行处理。李玲玲等[8]基于证据支持度的思想，针对DS理论处理严重冲突数据信息产生矛盾结论的现象，引入证据相容系数概念提出了一种新的证据权重的定义方法，提出证据可信度的概念并用组合规则进行数据融合。邱望仁等[9]分析并改进了证据理论中关于证据合成的方法，提出了一种新的多因素模糊时间序列预测模型。杜元伟等[10]分析了专家知识整体的结论缺乏科学性，而个体推断信息缺乏完备性和精确性，提出了基于证据理论/层次分析法(DS/AHP)的方法，能够从专家知识系统中提取到最优条件概率。

本文在增量式 GHSOM 的基础上，结合Dempster-Shafer理论提出了基于 DS理论的GHSOM入侵检测方法，在检测过程中对子网拓展规模进行动态控制，提升了在网络规模不断扩展时的动态适应性，在噪音环境下具有良好的检测准确率，提升了GHSOM入侵检测方法的扩展性。

2 GHSOM入侵检测模型

本文是基于增量式GHSOM入侵检测模型的研究基础上[7]进行，本模型学习过程首先是对将一个初始的数据集训练成相对成熟的GHSOM模型[4]，对该训练好的网络模型确定相似度阈值Sc，通过数据筛选动态生成神经元增量训练集It，对动态层拓展方案提出一种新的使用证据理论进行子网的拓展与规模控制的方案，将检测和学习两者同时进行，在检测过程之中对模型进行动态更新。

1) 数据采集。将提取到的每个检测模式映射向量x，加入到其自身的集合Mx中，通过比较得到可用于检测的获选神经元c。比较过程如下：若向量x与获选神经元c为同类，则要求x到c的最大距离d(x,c)必须小于相似度阈值Sc，则输出该检测向量为结果，否则认为当前检测向量与获选神经元不是同类，那么所有该神经元上的映射向量和被选向量都需要送入网络中进行再训练，其中有Sc满足

其中，wc为神经元c的权值，Mc为神经元c的映射向量集合，j为Mc中的任一向量。

2) 叶神经元集训练。首先将数据采集过程以及检测训练过程中得到的获选向量j都添加到获选神经元的增量训练集Mc中。在此情况下，若当前神经元c是获选神经元，则该神经元满足

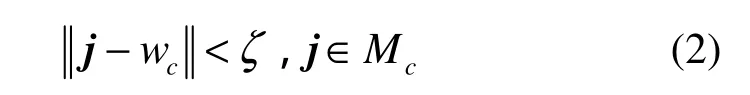
其中，ζ为经验常数。在检测过程中，只有不相似的被选向量才需要再次添加到增量训练集Mc中，这个过程就是不断地调整增量训练集Mc最终得到叶神经元训练集It。

3) 子网拓展。首先判断叶神经元调整的增量训练集It中的叶神经元t满足样本数

其中，k为正整数，若叶神经元样本数不满足子网拓展条件，则拓展过程回到叶神经元数据集增加中，否则以叶神经元数据集作为初始训练集，向下拓展得到虚神经元t′训练集，虚神经元t′是拓展过程中专门用于引导检测的神经元，定义其权值为映射向量中紧凑向量的平均权值。当由叶神经元t进行子网拓展时，首先从叶神经元向下进行拓展，得到对应的虚神经元t′，再以虚神经元t′为父神经元，对虚神经元t′引入证据推理，对其基本概率分配BPA设定为mθ，计算虚神经元t′的信任函数Bel(t′)，进行证据融合，剪去其中不符合条件的训练样本，对其余依旧满足numt的训练集进行拓展训练，进行递归拓展训练直至拓展层结构稳定下来。

4) 动态控制。当不断增长的拓展网络规模达到了子网剪去条件时，则执行子网回收，将不成熟的子网中的训练样本剪去并重新训练加到增量训练集Mc中，这样使过于庞大的子网结构获得精简。

3 DS理论的动态层拓展

基于DS理论的动态层拓展过程如图1所示。

在入侵检测的训练过程中，随着新增攻击类型的不断输入，增量训练集会动态地自适应拓展，带来的结果便是网络结构变得越来越大直至无法控制，因此当网络样本训练数达到numt时判定该增量训练集满足进行拓展训练的条件，对其进行拓展训练，生成一个相对成熟的新子网。其中Et通过实验方式获取。

以训练好的叶神经元数据集作为初始训练集，向下拓展得到虚神经元t′训练集，得到对应的虚神经元t′，将t′作为父神经元，对虚神经元t′引入证据推理，分配其基本概率BPA的设定为mθ，计算虚神经元t′的信任函数Bel(t′)，进行证据融合，以此作为判定条件剪去其中不符合条件的训练样本，对其余依旧满足numt的训练集进行拓展训练，进行递归拓展训练直至拓展层结构稳定下来。

在证据推理理论中，定义识别框架是由互不相容的基本命题所组成的完备集合，代表了对某问题的所有可能答案的表示，在这些答案之中只有一个是正确的。其中，将分配给各命题的信任度，即该框架的子集的信任程度称为mθ函数，即基本概率分配（BPA）。举例来讲，若mA表示对A的信任度大小，则称其为A的基本可信数。信任函数Bel(A)是用来表达对命题A的信任程度，似然函数Pl(A)表示对命题A非假的信任程度，也就是对A可能成立的不确定性的程度上的度量。总结来说，即[Bel(A),Pl(A)]表示A的不确定区间；[0,Bel(A)]表示支持命题A确认正确的区间；[0,Pl(A)]表示命题A的可能成立的区间；[Pl(A),1]表示命题A的绝对不成立的区间。在证据理论中，将一组行为不相交的假设称为辨别的一帧，例如(攻击，无攻击)。

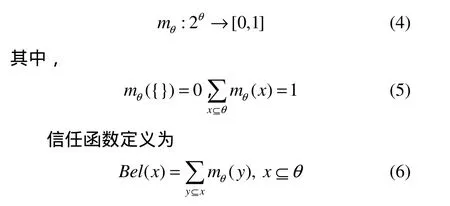
在GHSOM学习动态层拓展中，若用m1和m2来表示由互相独立的证据源(入侵检测中的传感器)所导出的基本概率分配函数，则使用Dempster组合规则进行信息的融合，用来计算这两者共同作用所带来的新的基本概率分配函数。设θ是识别框架，而mθ是一种BPA的基本概率分配组合的目标是从多个独立信息和计算中融合证据为一个整体的假说。独立意味着知道无论一个传感器是否值得信赖不会影响对于其他的可能性是否值得信赖的判断。一般地，如果2个传感器是独立的，则它们是工作在完全无关的功能部分用来确认受到攻击的可能性。若同时产生并发出了2个警报，则表明检测过程中的恶意行为是确信存在的。而要做的就是将2个来源的证据进行信息融合。一般来说，用Dempster规则进行融合

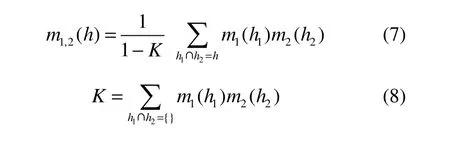
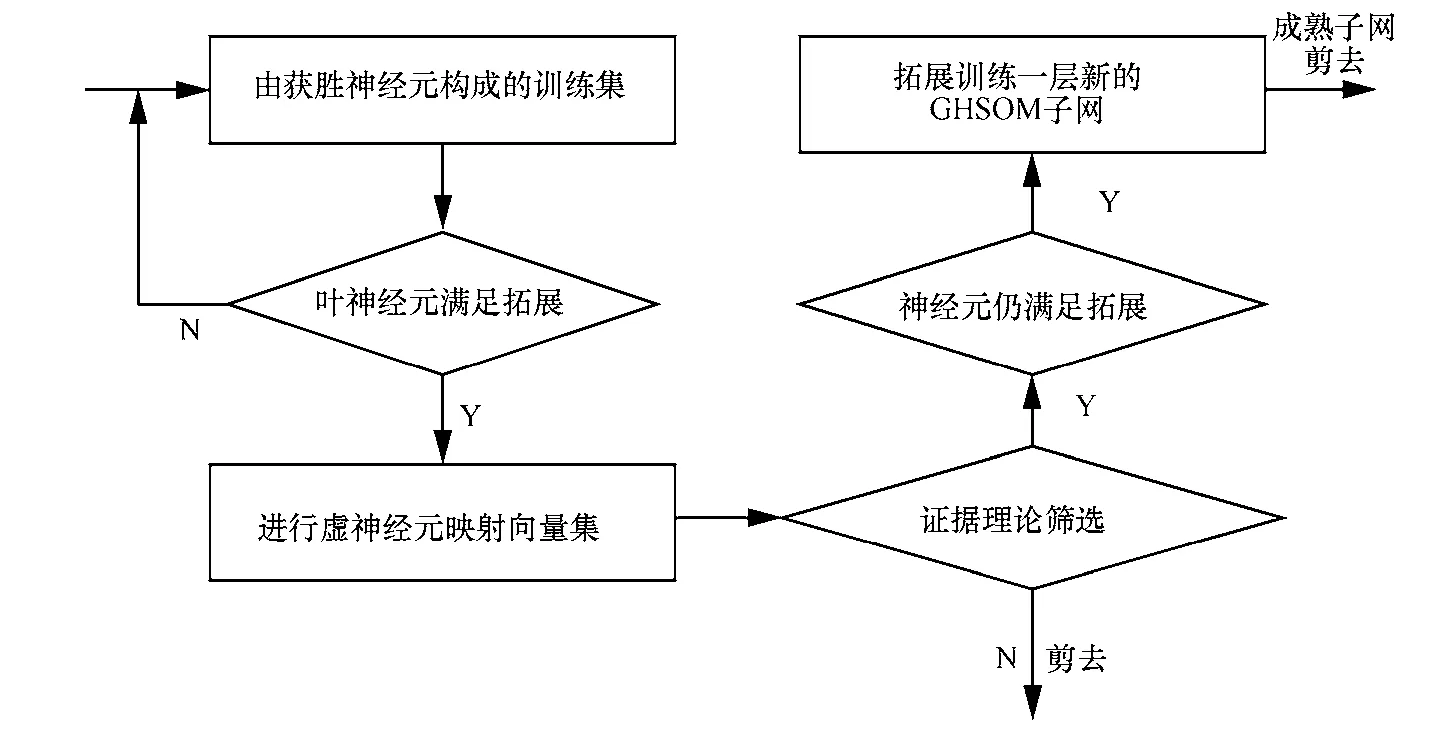
图1 基于DS理论的动态层拓展过程

其中，hi表示H的子集，表达的是各种假说均存在于识别框架之内。K是一个归一化因子，是一个在2个源之间的冲突的测量证据，这相当于在空集的情况下，测量hi之间的交集。

4 算法描述

基于证据推理理论的GHSOM学习动态层拓展算法是基于将一个初始的训练相对成熟的GHSOM模型在检测过程中进行动态自适应更新。首先算法的初始学习模型是以离线方式将样本数据集训练成相对成熟的GHSOM神经网络模型，然后进行算法的学习。基于Dempster-Shafer理论的增量式GHSOM学习动态层拓展算法步骤如下。

算法 基于Dempster-Shafer理论的增量式GHSOM学习动态层拓展算法

输入 成熟的以离线方式训练的GHSOM神经网络模型

5 实验与性能评估

实验采用Windows平台，使用KDD99的10%数据集作为检测样本，使用Matlab软件GHSOM神经网络分组对数据集进行训练。

实验过程中选取 PROBE、DOS、U2R、R2L这4种主要攻击类型进行攻击检测，选取其中的2种子类型作为网络中的新型攻击类型，剩下的攻击种类作为已知攻击类型。

首先使用Matlab软件GHSOM神经网络包对数据集进行初始训练，得到成熟的神经网路模型，对 KDD99数据集中的基于主机的网络流量统计特征中，前100个连接中，与当前连接具有相同目标主机相同源端口的连接所占的百分比设置基本概率分配m1，前100个连接中，与当前连接具有相同目标主机相同服务的连接中，与当前连接具有不同源主机的连接所占的百分比设置基本概率分配m2，使用证据融合规则进行数据筛选，缩小数据集。

对正常攻击类型和新型攻击类型进行实验比对，证明该方法对新型攻击类型有良好的检测率；对训练数据集进行子网拓展比对，证明该方法对子网拓展规模具有可控性。

6 结束语

本文在增量式 GHSOM 神经网络入侵检测模型深入研究的基础上，结合DS理论提出了基于证据推理理论的GHSOM神经网络入侵检测方法，当网络规模不断扩展时，首先处理大量数据不确定性中的随机性和模糊性问题，可以在噪音环境下保持良好的检测率，此外通过证据融合理论缩小神经元数据集，有效控制网络的动态增长。通过模拟实验对该方法进行了验证和评估，证实了方法的有效性和可行性，不足的地方在于未结合实际网络的大数据环境下进行比对，对可能出现数据随机性和数据短时间膨胀未进行深入探讨，这也将是研究工作的下一个重点。

[1] LUO Z Y, YOU B, XU J Z,et al. Attack graph algorithm in the application of intrusion detection system[J]. International Journal of Security and its Applications，2013, (9): 249-256.

[2] LUO Z Y, YOU B, YU G H,et al. Research of intrusive intention self-recognition algorithm based on three-tier attack graph[J]. ICIC Express Letters, Part B: Applications, 2015, (1): 1575-1580.

[3] 阳时来,杨雅辉,沈晴霓,等. 一种基于半监督GHSOM的入侵检测方法[J]. 计算机研究与发展, 2013, 50(11): 2375-2382.YANG S L, YANG Y H, SHEN Q N,et al. A method of intrusion detection based on semi-supervised GHSOM[J]. Journal of Computer Research and Development, 2013, 50(11): 2375-2382.

[4] 杨雅辉,姜电波,沈晴霓,等. 基于改进的GHSOM的入侵检测研究[J].通信学报, 2011, 32(1): 121-126.YANG Y H, JIANG D B, SHEN Q N,et al. Research on intrusion detection based on an improved GHSOM[J]. Journal on Communications,2011, 32(1):121-126.

[5] ZELL A, BAYER H, BAUKNECHT H. Similarity analysis of molecules with self-organizing surfaces—an extension of the self- organizing map[A]. Proceedings of the International Conference on Neural Networks[C]. 1994. 719-724.

[6] DENG D, KASABOV N.ESOM: an algorithm to evolve selforganizing maps from on-line data streams[A]. Proceedings of the International Joint Conference on Neural Networks[C]. 2000. 38.

[7] 杨雅辉, 黄海珍, 沈晴霓, 等. 基于增量式 GHSOM 神经网络模型的入侵检测研究[J]. 计算机学报, 2014, 37(5): 1216-1224.YANG Y H, HUANG H Z, SHEN Q N,et al. Research on intrusion detection based on incremental GHSOM[J]. Chinese Journal of Computers, 2014, 37(5):1216-1224.

[8] 李玲玲, 马东娟, 王成山, 等. DS证据理论冲突处理新方法[J]. 计算机应用研究, 2011, 28(12): 4528-4531.LI L L, MA D J, WANG C S,et al. New method for conflict evidence processing in DS theory[J]. Application Research of Computers, 2011,28(12):4528-4531.

[9] 邱望仁,刘晓东. 基于证据理论的模糊时间序列预测模型[J]. 控制与决策, 2012, 27(1): 99-103.QIU W R, LIU X D. Fuzzy time series model for forecasting based on Dempster-Shafer theory[J]. Control and Decision, 2012, 27(1):99-103.

[10] 杜元伟,石方园,杨娜. 基于证据理论/层次分析法的贝叶斯网络建模方法[J]. 计算机应用, 2015, 35(1): 140-146, 151.DU Y W, SHI F Y, YANG N. Construction method for Bayesian network based on Dempster-Shafer/analytic hierarchy process[J]. Journal of Computer Applications, 2015, 35(1):140-146, 151.