复杂网络中k-核与网络聚集系数的关联性研究

刘君，乔建忠

（东北大学 信息科学与工程学院，辽宁 沈阳 110819）

1 引言

复杂网络是一种新兴的网络研究理论，该理论正渗透到数理学科、生命学科和工程学科等众多不同的领域。学术界关于复杂网络的研究方兴未艾。特别是，国际上有2项开创性工作掀起了一股不小的研究复杂网络的热潮。一是1998年Watts和Strogatz在Nature杂志上发表文章，引入了小世界(small-world)网络模型，以描述从完全规则网络到完全随机网络的转变；二是1999年Barabási和Albert在Science上发表文章指出，许多实际的复杂网络连接度分布具有幂律形式[1，2]。近些年，对于复杂网络的研究出现了较多成果，大致可以分为 2类：1）结构分解类：理解真实世界中复杂网络（如Internet，WWW，细胞组织网络等）的体系结构并抽取出它们中紧密联系的部分——社团、结构洞、k-核等，发现它们之间的联系[3，4]。2）特征指标类：研究人员提出了一系列复杂网络特征（如介数、度分布、聚集系数等）来描述真实世界中复杂网络的拓扑结构。这些指标为宏观统计学角度研究复杂网络提供了非常有力的工具，例如通过统计Internet中节点的数据交互，分析获取 Internet拓扑结构的介数、度分布、聚集系数等特征，依据这些统计特征就可以设计相应的实模来仿真Internet的拓扑结构。

总体来看，目前关于复杂网络的研究多数只是停留在宏观统计分析上，通过对某一事件的关联数据进行统计，采用曲线估计、拟合等方法分析并找出规律，例如在文献[5]中，作者就Internet的拓扑结构突发性改变展开研究，通过统计大量Internet的数据来尝试解释突变的原因。宏观统计分析能够从统计学角度解释很多一直困扰让人的问题，但是由于数据的偶然性和时间的局限性，很难确保统计的样本量对于规律描述是充分的，此时需要一种科学客观的复杂网络拓扑结构描述理论。将宏观统计分析与该结构描述理论相结合能够更科学地解释一些现象，然而目前对于复杂网络拓扑结构描述理论方面的研究几乎处于空白。k-核解析是一种高效的图形分析方法，通过该方法，网络逐渐趋于核心的区域，一些研究人员给出了定性的结论：越中心的核，连通性越强。但是为什么会出现这种规律，连通性增强的幅度等问题均未回答。为此本文从k-核解析模型着手，研究了其数学意义，推导分析了该模型与网络聚集系数的关联性。得出的相关结论能够为k-核解析的进一步应用奠定相应的基础。

2 k-核解析模型

设图G= (V，E)是由|V| =n个节点和|E|=e条边所组成的一个无向图，则k-核的定义[6]如下。

定义1k-核（k-core）。由集合C⊆V推导出的子图H=(C，E|C)，当且仅当对C中的任意节点v，其度值均大于或等于k，即∀v∈C： degreeH(v)≥k，具有这一性质的最大子图就叫作k-核。核中包含的节点数目则称为核的大小。依据k-核的定义，图G的k-核就可以通过反复地移去那些度值小于k的节点以及与其连接的边，直到余下图中所有节点的度值都大于或等于k来得到。因此可以通过k-核解析由外层至内层一层一层地解析网络，直到最内层为止，从而揭示网络的层次结构性质。

图1所示为k-核解析的流程。首先按照k-核定义去掉图1中度值为1的黑色节点及其边，剩下的由灰色与白色节点构成的拓扑图即为2-核；然后去掉度值为2的灰色节点，剩下的由白色节点构成的拓扑结构图为3-核。需要注意的是，若图1中出现Y4节点，按照核解析的定义，需要反复去掉度值为2的节点，因此{Y1，Y2，Y3，Y4}都将会在2-核解析过程中被去除，即虽然它们初始度值不同，但是最终都属于2-层节点。

3 k-核与聚集系数关联性分析

大量文献给出了关于k-核解析的定性描述：高核内节点的连通性高、传播性强。但是连通性、传播性到底代表什么，用什么来表示，均未给出详细定量的描述。本文将连通性、传播性统称为小世界特性，并引入网络直径与聚集系数概念来表征网络小世界特性的强弱。网络直径越小、聚集系数越大的网络小世界特性越强，反之越弱。

图1 k-核解析示意

定义 2节点聚集系数(clustering coefficient)[7～9]。某节点i的聚集系数为该节点所有邻居节点之间连接数目占可能的最大连接数目的比例

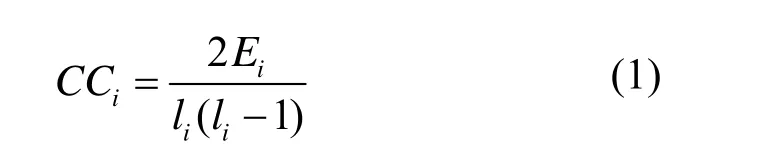
其中，li为节点i的邻居节点个数，Ei为这li个节点之间存在的连接数目。一个网络的聚集系数为网络中所有节点CCi的均值C。节点聚集系数是反映节点在网络连通性特征上贡献的一个重要指标。网络聚集系数是反映网络拓扑结构连通性、传播性的一个关键因素。

定义 3网络直径。指网络中任意两节点间跳数的最大值[10，11]。网络直径与聚集系数共同确定着网络小世界特性的强弱。例如图2(a)网络的网络直径为6跳，网络聚集系数Ca为

由此可以看出图 2(b)网络的小世界特性较图2(a)网络的小世界特性强，即连通性、传播性均要高于图2(b)网络。因此在图1给出的网络拓扑基础上进行k-核解析满足上文提及的“高核对应着高连通性与传播性”结论。但是是否在任意给定的拓扑结构中这一结论均成立？下文将围绕这个问题对命题1展开论证。

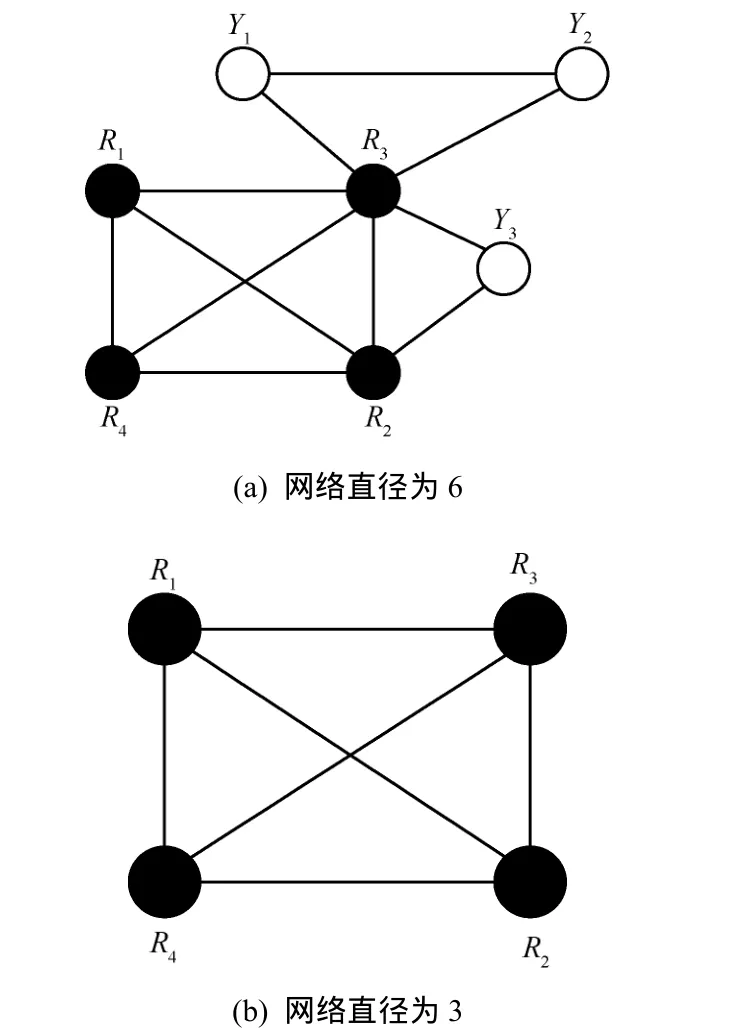
图2 k-核解析局部示意

命题1在给定网络拓扑上，不断进行k-核解析，若k核对应的网络聚集系数为Ck，k+1核对应的网络聚集系数为Ck+1，则有Ck+1＞Ck；若k核对应的网络直径为Dk，k+1核对应的网络直径为Dk+1，则有Dk＜Dk+1。

证明 首先关于网络直径的变化：由k-核解析的定义可知，随着核数的增加，k核变为k+1核时，网络中节点数目是减少的，且节点间的连边也是只有减少没有新增。所以网络中两点间最大跳数不可能增加，即Dk＜Dk+1。其次关于聚集系数的变化，对式(1)进行变形

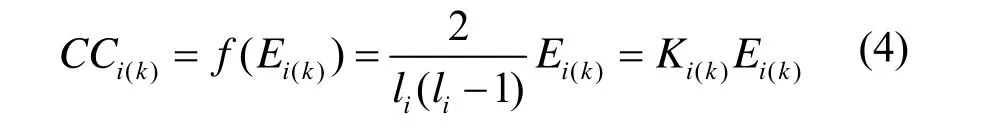
在任意结构中，k-核内节点i的邻居节点数ki为常数，能影响k-核结构中节点i聚集系数的因素为Ei(k)。此外通过式(4)可以看出k核中节点i的聚集系数CCi(k)与k核拓扑中节点i的邻居节点间连边数目呈离散线性方程关系，其中，Ki(k)为k核中节点i对应方程系数。

图3为拓扑由k-核向k+1-核解析的示意，k-核内节点I、J的度值为dJ(k)与dI(k)，且 dJ(k)＜dI(k)。节点I为J的邻居节点，在该次解析过程中按照k-核解析的原则将被去除，且J节点能够保留在更高核内。当节点I被去除时，对于拓扑中其他剩余节点对应聚集系数将会有2种结果：保持不变或改变。

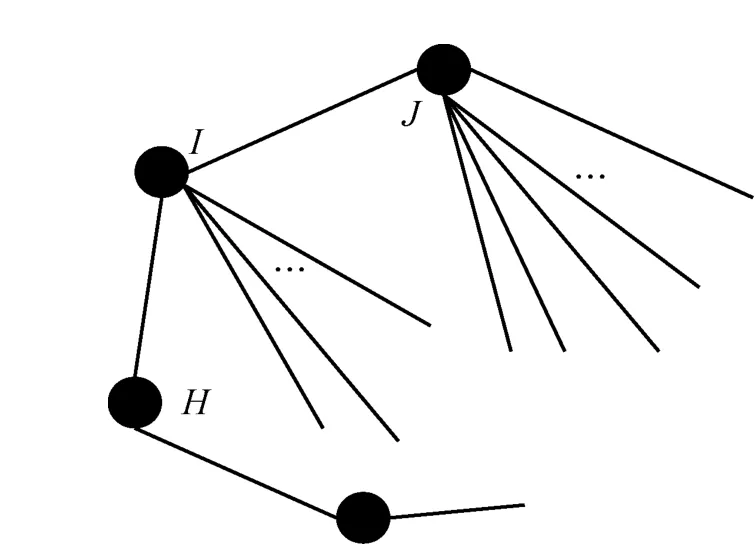
图3 k-核向k+1-核解析示意

本文主要讨论节点I被去除后聚集系数发生变化的节点。例如以图3中的节点J为例，节点I为J的邻居节点，且节点I与J的其他邻居节点存在连边，则I的去除将会影响节点J的聚集系数。由于给定拓扑的聚集系数与拓扑内部连边数目呈过原点的线性关系，如图4所示，因此，只需要确定式(4)线性方程中的Ki(k)即可确定k-核与k+1-核对应的线性图。从图4中可以看出，若k-核解析后节点J的邻居节点间连边数目相等，即EJ(k)=EJ(k+1)，则k+1核中节点J对应的网络聚集系数大于k核中节点J对应的网络系数。

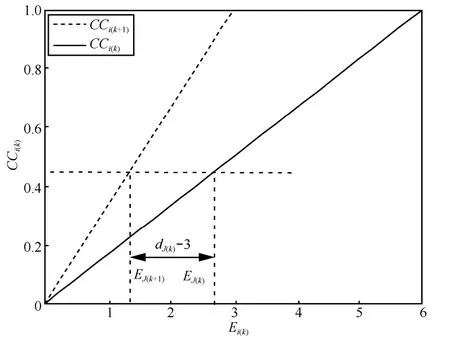
图4 聚集系数与Ei的线性方程

然而由于k-核解析，I节点被去除后，导致了k+1核中连边数目发生了减少，即I被去除后，KJ(k)＜KJ(k+1)，但是EJ(k)＞EJ(k+1)，难以确定最终节点J聚集系数的变化。对于图3给出的拓扑结构，按照k-核解析的原则可以得出如下推论。

1) 由于k-核中节点J的度值为dJ(k)，因此，k-核中节点I的度值dI(k)最大为dJ(k)-2，因为若dI(k)=dJ(k)-1，则当I被去除后节点J的度值也将变成dJ(k)-1，依照k-核解析定义，J节点也将被去除，这与原设定不符。

2) 当k-核内节点I被去除后，(k+1)-核中节点J邻居节点连边数目相对于k-核中节点J邻居节点连边数最多减少dJ(k)-3条，即EJ(k)-EJ(k+1)＜=dJ(k)-3，因为即使节点I在k-核内取最大度值dJ(k)-2，节点J邻居节点连边数目中I节点的所占据的连边数目应为I的度值减去I与J之间的一条连边，即为dJ(k)-2-1。

3) 当k-核内节点I被去除后，k+1-核内每个节点度值最小为dI(k)-1，因为若某个节点度值为dI(k)-2，则该节点将与节点I一起被去除。

图 4中给出了k-核、(k+1)-核中聚集系数的函数直线，可以看出，EJ(k)与EJ(k+1)的差值若可以取任意值，则CCJ(k)与CCJ(k+1)的大小无法确定。但是通过上述结论可知EJ(k)与EJ(k+1)的差值最高为dJ(k)-3，在这个限制下CCJ(k)与CCJ(k+1)存在何种大小关系呢？

从图 4中可以看出在给定某个EJ(k)值的前提下，随着EJ(k)与EJ(k+1)的差值由零逐步变大，将会依 次 出 现CCJ(k)＜CCJ(k+1)、CCJ(k)=CCJ(k+1)和CCJ(k)＞CCJ(k+1)的关系。EJ(k)与EJ(k+1)的差值越小，则CCJ(k)＞CCJ(k+1)越不可能出现。因此，若当EJ(k)-EJ(k+1)=dJ(k)-3 时，CCJ(k)＜CCJ(k+1)，则可以得出结论：无论EJ(k)取何值，k+1-核对应的聚集系数将大于k核对应的聚集系数。当EJ(k)-EJ(k+1)=dJ(k)-3时，假设式(5)成立

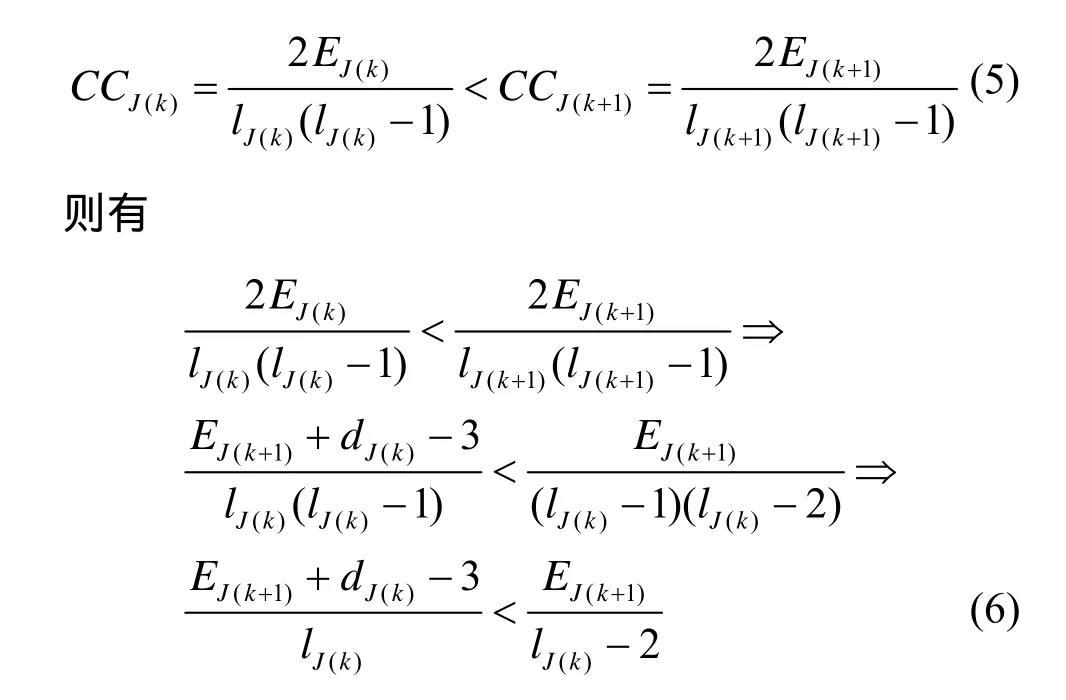
又因为图3中节点J的度值就是节点J邻居节点的个数，因此dJ(k)=lJ(k)，所以式(6)可以演化为

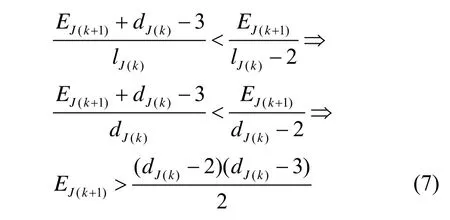
由于节点I取得度值为dJ(k)-2，所以在k+1-核内每个节点的度值最小为dJ(k)-1，去除与节点J的连边。则在k+1-核内，节点J的邻居节点共有dJ(k)-1个，每个节点度值最小为dJ(k)-2。通过拓扑学不难得出，这dJ(k)-1个度值最小为dJ(k)-2的邻居节点，构成的拓扑就是全连通拓扑结构，此时的EJ(k+1)为

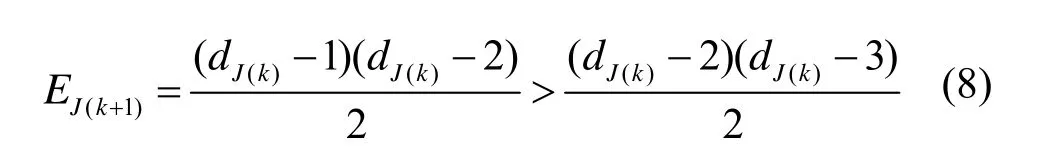
式(8)证明了式(7)的成立，因此假设成立，即CCJ(k)＜CCJ(k+1)。

通过上述证明可以得出2点结论。

1) 在k-核解析过程中若被去除节点I的度值为dJ(k)-2，则k+1核中节点J的邻居节点间将为全连通结构。

2) 在给定拓扑结构中进行k-核解析使拓扑结构由k-核变为k+1-核，当去除一个低度值节点I时，若I节点的去除对原拓扑结构中节点J的聚集系数产生影响，且节点J保留至高核中时，则节点J在k+1-核中对应的聚集系数大于k-核中对应的聚集系数。即随着k-核解析的进行，高核节点的聚集系数保持不变或者增高。

由上述结论不难看出，随着低核节点的逐个去除，一方面导致高核中节点数目的降低，另一方面保留在高核中各个节点的聚集系数只增不减，因此高核拓扑结构最终对应的网络聚集系数将会增加，即命题1成立。至此，关于命题1的证明结束。

4 实验及仿真

为了检验命题1的正确性，本文设计了一个实验，首先实现了Les Miserables网络生成方法[12]，生成了一个复杂网络，构建了网络拓扑结构布局，然后借助于Gephi复杂网络性能分析平台，逐步进行k-核解析，统计每一个k值对应的网络聚集系数。若随着k值的增加，网络聚集系数呈增长趋势，则能够验证命题1的正确性。实验相关的设置如表1所示。

表1 网络仿真参数设置

图5显示了表1仿真环境下，不同k值设定下的网络拓扑结构分解图，可以看出，随着k值的增加，网络中节点越来越少，当k=10时，网络消失，因此表1给出的网络拓扑最高核为9。此外当k=5与k=6时，网络拓扑结构没有发生变化，因此当k=5时的网络拓扑结构中所有节点度值均大于6。

图5 k-1核解析分解

各个k值对应的网络聚集系数如表2所示。

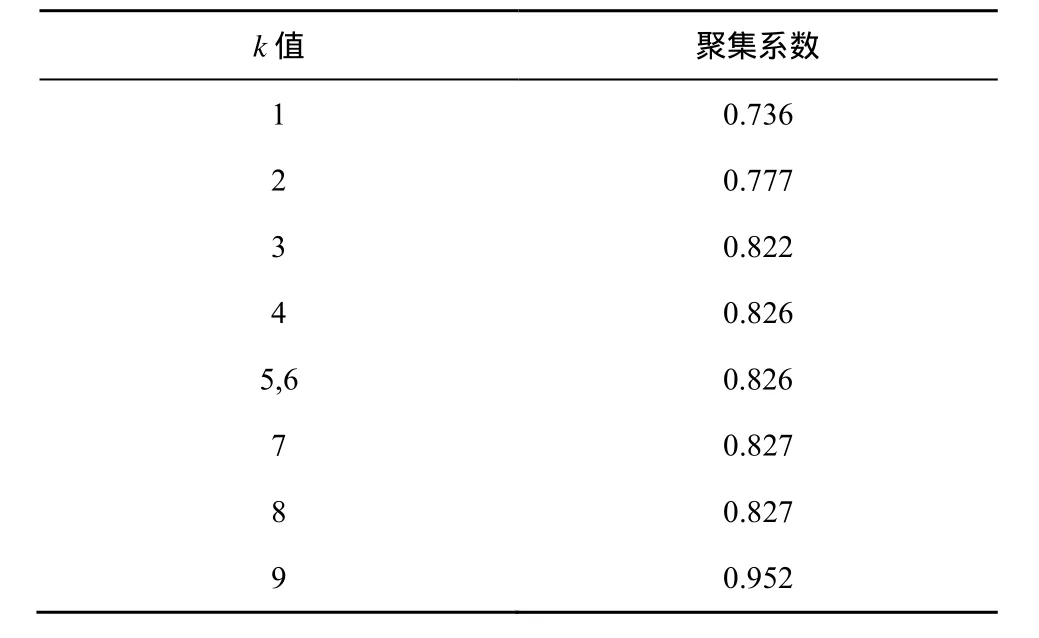
表2 k值与网络聚集系数的对照

从表 2可以看出，随着k-核的不断解析、k值的不断增加，网络聚集系数呈现逐步增加的趋势，该仿真测试结果与定理1相吻合。

5 结束语

本文主要对k-核解析与网络聚集系数之间的关联进行了论证研究。k-核解析是一种复杂图分解的常见方法，但是随着k-核的不断分解，高核结构所体现出的特性到底如何变化是一项研究空白，本文针对网络聚集系数这一特性，展开了研究。通过理论推导与证明，明确了k-核分解与网络聚集系数之间的关联，即越高核对应的网络聚集系数越高，在此基础上设计了实验检验理论证明。本文得出的结论可以与现有宏观统计分析方法相结合，为复杂网络应用提供相应的理论基础，例如重要节点或者结构发掘研究、网络抗毁性研究等。以文中实验为例，当9-核网络对应的聚集系数为0.952，这表明该网络中的小世界性很高，具有高传播性和高抗毁性，对病毒预防领域中，该结构的危险性最高，通过本文后续研究能够找出最优结构调整策略，在微小删边代价下重构9-核，将能大大提高网络病毒免疫能力。

在后续工作中，本文将重点研究网络节点、边的价值属性，即当删除/添加一个节点或者一条边对网络的聚集系数以及其他特征参数所产生的影响。k-核解析在某种意义上也是一种节点、边的删除行为，但是本文只是通过推导证明了k-核分解会造成网络聚集系数的增加，但是并没有给出具体增加的幅度。通过后续工作的研究，能够为k-核解析提供一种全新的量化视角。

[1] 汪小帆， 李翔， 陈关荣. 复杂网络理论及其应用[M]. 北京：清华大学出版社， 2006.49-70.WANG X F， LI X， CHEN G R. Theory and Applications of Complex Network[M]. Beijing： Tsinghua University Press， 2006.49-70.

[2] SONG C， HAVLIN S， MAKSE H A. Origins of fractality in the growth of complex network[J]. Nature Physics， 2006， 2(4)： 275-281.

[3] GOH K I， SALVI G， KAHNG B，et al. Skeleton and fractal scaling in complex networks[J]. Physical Review Letters， 2006， 96： 018701.

[4] GUO Q Z，et al. Exploring the local connectivity preference in Internet AS level topology[J]. Piscataway， 2007， 13(1)： 6439-6445.

[5] ZEGURA E W， CALVERT K L， DONAHOO M I. A quantitative comparison of graph-based models for internet topology[J].IEEE/ACM Trans on Networking， 1997， 5(6)：770-783.

[6] ONNELA， J. SARAMAKI， HYVONEN J. Structure and tie strengths in mobile commutation networks[J]. PNAS， 2007，104(18)： 7332- 7336.

[7] BARCELÓ J M， NIETO-HIPÓLITO J I， GARCIA-VIDAL J. Study of Internet autonomous system interconnectivity from BGP routing tables[J]. Computer Networks， 2004， 45(3)：333-344.

[8] DIMITROPOULOS X， KRIOUKOV D， FOMENKOV M，et al. AS relationships： inference and validation[J]. SIGCOMM Computer Communications Review， 2007， 37(1)：29-40.

[9] PARK S T， PENNOCK D M， GILES C L. Comparing static and dynamic measurements and models of the Internet's topology[A]. Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies[C]. 2004.1616-1627.

[10] ZHOU S， MONDRAGON R J. The rich-club phenomenon in the Internet topology[J]. IEEE Communication Letters， 2004， 8(3)：180-182.

[11] ZHOU S， MONDRAGON R J. Structural constraints in complex networks[J]. New Journal of Physics， 2007， 9(172)：1-11.

[12] KNUTH D E. The Stanford GraphBase： A Platform for Combinatorial Computing[M]. Addison-Wesley， Reading， MA， 1993.