中国高储蓄率的测度与动态影响机制研究
2015-01-01刘尧成
刘尧成,顾 淳
(苏州大学 商学院,江苏 苏州215021)
一、引 言
中国自改革开放以来国内生产总值实现了9%以上的平均增长速度,创造了国际上经济长期高增长的奇迹,但与此同时,中国经济结构失衡的情况却越来越严重,其主要表现就是储蓄率不断上升而消费率不断下降。改革开放以来,中国储蓄率基本上呈现一个上升的趋势,从1978年的36%上升到2013年的51%,平均每年上升0.42%,被称为“中国高储蓄之谜”。
中国高储蓄率问题对国内外都有深远的影响。一方面,在当前中国对外出口受阻等经济环境下,降低储蓄、刺激消费以扩大内需,最终实现经济结构转型升级,成为支撑中国经济可持续发展的关键;另一方面,由于中国对世界经济的影响越来越大,中国的高储蓄率也受到了国际的高度关注甚至指责,例如美联储前主席伯南克就将中国等新兴市场经济国家“由过高储蓄率导致的经常账户顺差和外汇储备积累”作为2007年国际金融危机的罪魁祸首①①Bernanke,2009,Financial Reform to Address Systemic Risk.Speech at the Council on Foreign Relations.。
上述分析表明当前中国迫切需要降低储蓄提高消费,为此,必须对“中国高储蓄之谜”做出解释。目前有关“中国高储蓄之谜”的解释已经有很多,其中具有代表性的有如下几种:一是人口结构论。认为人们会为平滑自己一生的消费而在不同年龄阶段进行储蓄决策,因此一个国家的人口结构就成为决定该国居民储蓄率的一个重要变量。Modigliani和Cao发现中国储蓄率与长期经济增长率及抚养比存在着协整关系,进而将中国的高储蓄率主要归结为高经济增长和人口结构的改变,按照这种理论进行的研究还有李文星、汪伟等[1-3]。二是制度因素论。认为社会保障制度不健全等所带来的不确定性是造成中国高储蓄低消费的原因,这方面的研究有李佳峰和刘尧成以及方丽婷和钱争鸣等[4-5]。三是政策影响论。李永友和吕冰洋认为中国特殊的财政制度安排恶化了中国居民的消费倾向,从而加速了中国的经济结构失衡[6-7]。林毅夫和姜烨以及郭新强等则从中国金融系统存在金融压抑的视角,探讨货币政策冲击对于中国储蓄率和消费率等结构性失衡的影响[8-9]。
综上所述,已有的文献对中国高储蓄率问题进行了较为全面的探讨,但是仍然存在如下两方面的不足:首先,已有的文献主要对中国高储蓄率的原因展开分析,但是中国高储蓄率的原因有很多,无从判别哪一种因素更为重要②② 周小川在《关于储蓄率问题的思考》一文中指出,影响中国储蓄率的不确定性因素很多,目前尚无充分可信的学术研究说明中国储蓄率的高低与某种特定的因素如人均收入、消费习惯等相关。引自中国人民银行网站,2009年11月26日。;其次,已有的文献主要从方向上解释中国储蓄率为何偏高,而对于偏高的程度缺乏量化分析,尤其是对偏高程度不断上升的事实缺乏解释。因此,能否解释中国储蓄率逐步上升的趋势应该是判断理论研究是否具有说服力的标准。本文基于“缓冲存货”模型对上述两个不足进行补充。本文并不试图分析某种特定因素对于中国储蓄率动态的影响,而是将所有的不确定性冲击因素统一成一个随机冲击项,并考虑该随机冲击的程度变化(即随机冲击方差)的影响,是对已有“缓冲存货”模型的一个扩展。
二、中国高储蓄率的含义与测度
不同经济体在经济发展的不同阶段合理储蓄率的边界是不一样的,因此,如果仅进行国别比较,显然很难得到中国储蓄率偏高的结论,也难以理解“中国高储蓄率之谜”。但是,依据传统的经济增长理论,一国经济的发展最终是为了满足其居民跨期的最大化消费,因此在每一期都应该有一个最优储蓄率,在均衡时即为经济增长的“黄金分割率”。黄金分割率由一国的经济增长率g、人口增长率n和资本折旧率δ决定,如果假设n和δ为常数,则最优储蓄率就只与一国的经济增长率相关。为了判断中国储蓄率是否偏高,通过建立一个基准的经济增长模型并结合中国的实际情况进行参数校准,求得中国的“最优储蓄率”,即该模型预测的中国储蓄率的理论值,以与中国储蓄率的实际值相比较,从而测度中国储蓄率偏高的程度。这种方法对中国高储蓄率进行的测度具有理论基础,而且能够进行国际比较,也可以直观地观测到储蓄率自身的动态演变。
通过一个简单的基准经济模型来说明储蓄率与经济增长率的关系。设一个完全竞争的经济环境,则一个基准的经济增长模型可写为代表性经济行为人i面临的如下一个动态规划问题:

其中和分别为行为人i在t期最优选择的消费、劳动投入和储蓄为其上一期的储蓄,为经济增长率由竞争决定的工资水平。为分析简便,假定人口增长率为0。为了和下文所建立的模型进行区别,本文将上述模型记作“模型A”。
为求解模型A,首先对和进行一阶求导,分别得到下式:

式(3)至(5)中的λit为约束式(2)的拉格朗日乘子,rt为完全竞争市场上的利率。本文假设一个标准的Cobb-Douglas生 产 函 数:yit= (kit)α,其 中kit=为集约形式的资本。则由完全竞争条件下的资本市场出清条件可得:

式(6)中δ为资本的折旧系数。由于代表性经济行为人i既是消费者又是生产者,则其t期的资本就等于其储蓄,即kit=sit,因此将式(6)和(7)代入式(2)即可得到行为人i的预算约束条件:

式(8)左边为行为人i在第t期的消费加上净储蓄,右边为其在t期的可支配收入,则行为人i在t期的储蓄率可定义为:。由于i为代表性经济行为人,该式即为模型A所预示的该国储蓄率。在稳态时,上式可写为:τ=。将式(6)代入式(5)可得稳态时的k/y值为。则模型A稳态时的储蓄率可表示为:

从式(9)来看,当α、β和δ等经济参数确定以后,模型A显示一国稳态时的储蓄率只与其稳态的经济增长率有关,且有τA/g>0。为了进一步解析模型A对中国储蓄率的解释和拟合情况,结合中国的实际情况对式(9)中的经济参数进行校准。首先,α描述的是资本收入占总收入的比重,西方经济学研究中一般设其为0.3,但考虑到当前中国资本收入占总收入比例较高的现实,张军在对中国问题的研究时将α设为0.49,本文设置α为0.5[10]。其次,对于主观贴现率β和资本折旧系数δ,由于其在各国差异并不大,在本文分析的时间频度为年度的情况下,遵从大多数文献分别设其为0.96和0.1。
在以上对模型A的参数进行校准之后,还须对稳态的经济增长率赋值才能求解出稳态的储蓄率。由于稳态时的储蓄率只与经济增长率有关,为了简化分析,假设样本时段内中国的经济增长率在每个年度都处于均衡的稳态,这样就可以将每年的经济增长率作为均衡经济增长率代入式(9)进行一种比较静态均衡分析①①由于我们只分析均衡经济增长率变化的影响,因此是一种比较静态均衡分析。,从而得到模型A对当年中国储蓄率的模拟值(记作τA,t),该理论值代表的即为中国最优的储蓄率。比较中国储蓄率的实际值(记作τt)和模型的理论值,就可以观测到中国储蓄率是否偏高,以及偏高的程度(包括偏高幅度与偏高比例),其结果如图1所示。

图1 中国高储蓄率的数值模拟及测度(1978-2013年)
图(a)中“实际值”为中国储蓄率,“理论值”为模型A对中国储蓄率的数值模拟值;图(b)中“偏高幅度”为实际值减去理论值,“偏高比例”为偏高幅度与理论值的比值,虚线为偏高比例的趋势线。图(b)的左纵轴为偏高幅度坐标轴,右纵轴为偏高比例坐标轴。
首先,图1(a)显示样本时段内中国储蓄率的实际值始终高于基准模型预测的理论值,表明中国储蓄率确实偏高。式(9)表明储蓄率与经济增长率呈正比例,但即便考虑中国长时期高达9%以上的经济增长率,图1(a)显示中国合理的储蓄率也应该稳定在20%至30%的区间,但中国储蓄率实际值却一直维持在35%至50%;其次,图1(b)显示了中国储蓄率的偏高幅度和偏高比例,可见中国储蓄率偏高的幅度和偏高的比例呈逐步上升的趋势。从偏高比例的趋势来看,从1978至2013年中国储蓄率的偏高比例平均每年上升1.52%,至2013年中国储蓄率实际值高于理论值的比例已经达到了80%。因此,应用传统理论无法解释中国储蓄率长期偏高且偏高程度不断上升的事实,这也是“中国高储蓄率之谜”一直没有合理解释的重要原因,所以解释“中国高储蓄率之谜”的关键在于如何解释中国储蓄率偏高程度不断上升的特征事实。本文通过建立模型对上述经验事实进行模拟分析。
三、储蓄率动态中的金融加速器效应分析
上述模型的分析和结论是基于一个基准的经济增长模型,其理论假设与中国的实际情况至少有如下两方面的差距:首先,允许居民间自由借贷,但中国存在着严重的金融压抑,因此本国居民存在着严重的信贷约束;其次,分析的是一个确定性的经济环境,这与改革开放以来中国陆续推进的住房、医疗改革以及国外金融危机冲击等一系列因素给中国居民所造成的不确定性不相符合。实际上,在随机冲击下,由于存在信贷约束,居民将不得不增加储蓄来缓冲未来的不确定性,这就是传统“缓冲存货”模型的基本思想。本文将应用“缓冲存货”模型并对其进行扩展,来研究信贷约束下随机冲击对中国储蓄率动态的影响机制。
(一)模型设定与求解

将由式(10)~(12)构成的模型称为“模型B”。其中式(10)所示的信息集反映了行为人i的上述决策顺序。式(11)中[(1+rt)sit+wtnit]即为行为人i在t期的总资产,将其记为从式(11)看,随机冲击发生后,行为人i总资产的波动幅度取决于随机冲击的波动幅度。本文将的波动变化幅度称为随机冲击的程度的波动幅度变大表示随机冲击的程度加大,反之则变小。
按照上述假设,由于经济行为人i必须在冲击发生前做出劳动供给决策,而且所有行为人所面临未来冲击的期望都是相同的,调节一单位劳动所付出的成本也是一样的,因此不同的行为人会通过调节其劳动供给将冲击前的资产调整至相等,即对于不同的行为人i,j,…,有成立。此时,将式(6)和式(7)所示的rt和wt代入,可得,即为冲击发生前行为人i手中已有的资产。

上述两式中的λit和πit分别为约束式(11)和(12)的拉格朗日乘子。将式(13)代入式(14),并利用期望迭代法则可得:
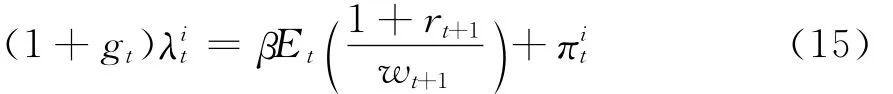

此时,为了使得πit不至于小于0,易知,即不同的行为人i维持同一消费水平时,多余的资产则会被储蓄以应对下一期可能遭遇到的不利冲击,进而可得:

情形2:εit<ε*t。按照以上对情形1的分析,此时有πit>0成立,即行为人i有借贷的需求,但是由于存在借贷约束而得不到满足。此时行为人i会将所有的资产用来消费,即则由式(3)可知此时的值为:

根据以上对两种情形的讨论,行为人i会在遭受随机冲击εit后平滑其消费;如果,行为人i会增加其储蓄,以减轻下一期可能的不确定性,即行为人i会通过调节其储蓄的多寡进行一种“缓冲存货”来达到平滑消费的目的,因此上面建立的模型即为“缓冲存货”模型。根据大数定律,经济中总的消费和储蓄可分别表述为:

其中:

再定义可支配收入Dt=ct+(1+g)st+1-st,则此时的储蓄率τB,t可定义为:

将式(16)和(17)表示的两种情形下的λit式代入式(13),可得如下欧拉方程式:


(二)金融加速器效应分析
为了简化分析,仍然对模型B进行比较静态均衡分析。按定义稳态时的储蓄率τB仍然为(gk)/(y-δk)=g(k/y)/[1-δ(k/y)],为此需求出模型B中稳态的k/y值。将式(6)带入式(18)即可得此时的k/y值,从而可得模型B稳态时的储蓄率τB:

比较式(9)和式(22),τA与τB的关键区别在于R(ε*)。由于,而且,所以在相同的稳态经济增长率下有,由此可以得到如下推论1。
推论1:在存在信贷约束时,经济行为人为缓冲随机冲击而节制当前消费以向未来提供储蓄的收益存在着“流动性溢价”,从而使得行为人倾向于增加储蓄而减少当前的消费,因此储蓄率与“流动性溢价”成正比例变动。
为了量化分析随机冲击对储蓄率的动态影响机制,将对上述的缓冲存货模型进行扩展分析。首先,由式(21)来看,为了求解出,必须先确定θt和。为此,设,则代表一种“临界点消费率”,使得冲击发生后居民拥有的资产刚好平滑其消费,既无需借贷也没有储蓄。从而可知:
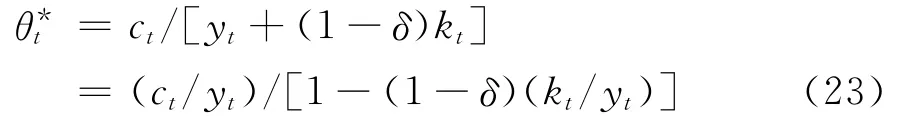
式(23)显示在稳态时θ*和ε*间存在着函数关系。由于ε*t可以表示为ε*t=θ*t-θt,因此求解该模型的关键是如何求得每年的θt。为此,设θt= (1-ρ)θ*t,则有:

式(24)即本文对现有的“存货缓冲”模型所做的扩展。这种扩展不仅可以极大程度地简化模型求解,而且还有明显的经济学含义,即ρ值的变化反映了随机冲击εit波动幅度的大小,ρ值越大代表随机冲击程度越大。进一步的分析ρ值的变化趋势和流动性溢价R(ε*)的关系。将式(24)代入式(21),在稳态时式(21)可改写为下式:

式(24)和(25)显示θ*和R(ε*)可写作g和ρ的函数,结合式(20)可以求得ε*,从而进一步求得θ*和R(ε*),再由式(22)可得到模型B的储蓄率τB随g变动趋势。因此,可以分析临界点消费率θ*、流动性溢价R(ε*)和储蓄率τB随经济增长率g的变动,由于g是一种均衡经济增长率,因此这是一种比较静态均衡分析,图2即为结果。图中模拟出了均衡增长率g从0变到1时θ*、R(ε*)和τB的变化情况,其中考虑了ρ值依次为0、0.25、0.5、0.75和1等五种情况,代表着随机冲击程度不断变大的趋势。

图2 经济增长率g变化的比较静态均衡分析图
从图2(a)和图2(b)来看,当ρ值保持不变时,随着经济增长率g从0逐步上升为1,θ*呈单调下降而R(ε*)单调上升。另外,图2(a)和图2(b)显示,当经济增长率g保持不变时,随着ρ值从小变大,θ*逐步变小而R(ε*)逐步变大。图2(c)显示储蓄率会随着经济增长率上升而上升,而经济增长率相同的情况下,随机冲击程度加大会放大储蓄率上升的程度,其逻辑分析与上面对R(ε*)和θ*的分析一致。根据图2的分析我们就可以得到如下的推论2。
推论2:随机冲击引起的“流动性溢价”与经济增长率成正比,且与随机冲击的程度也成正比。
从上述两个推论就可以得到存在信贷约束和随机冲击时储蓄率动态的金融加速器效应:即随机冲击程度与“流动性溢价”呈正比,而“流动性溢价”与储蓄率成正比,则储蓄率与随机冲击程度成正比。因此,正是由于随机冲击这种摩擦致使“流动性溢价”存在,加剧了经济增长率对于储蓄率动态的影响,由于本文假设了随机冲击在生产决策之后才被观测到,这与Bernanke等人建立的金融加速器效应所论述的信息不对称等摩擦性因素加剧经济波动的原理是一致的,因此上述动态机制就构成了储蓄率动态中的金融加速器效应[12]。
四、对中国储蓄率动态的数值模拟
由上文上分析得到的储蓄率动态中的金融加速器机制,其存在依赖于两个前提,即存在着信贷约束和随机冲击,这与中国经济的现实情况是相符合的。因此,可以应用上述模型对于中国储蓄率的波动进行数值模拟。
首先,可以分析中国储蓄率动态脉冲响应情况,为此需要定义一个一般均衡系统。由式(6)、(8)、(18)、(19)、(20)、(23)和(24)即可得到一个一般均衡系统,由该经济系统可以得到经济变量的唯一解,由此可得到这些经济变量对经济增长率gt变化一单位的动态响应。由于上文的经济参数值都是根据中国的实际情况进行校准而得,可以分析得到中国储蓄率对一单位经济增长率gt变化的脉冲响应结果,如图3所示①①我们对中国经济增长率的周期性波动成分进行一阶自回归分析,发现一阶自回归系数为0.69,因此在进行脉冲响应实验时假设,其中为白噪声。。图3显示1%单位的经济增长率冲击下,中国储蓄率的脉冲响应有一个“驼峰”的反应形状,其在第二年即达到最高值,随后逐渐下降,大约在第10个年度储蓄率收敛到初始稳态。图3显示,当不存在金融加速器机制时(即ρ=0),储蓄率最高值为0.3,而当存在金融加速器机制且随机冲击程度达到最大(即ρ=1)时,该最高值达到了0.75,是没有金融加速器时的2.5倍。因此,储蓄率动态中金融加速器效应的存在为解释图2中国储蓄率大幅偏高,且偏高程度不断上升的事实提供了可能性。

图3 1%经济增长率冲击下中国储蓄率的脉冲响应图
为了进一步模拟中国储蓄率的波动情况,仍可进行比较静态均衡分析,以分析模型B对于中国储蓄率动态的模拟情况。根据式(22),只需要给出中国每一年的随机冲击程度ρt的值。为了确定1978年和2013年的ρ值,将不同的数值作为1978年和2013年的ρ值带入模型进行模拟运算①①我们也可以应用中国储蓄率和经济增长率数据推导出中国每年的ρ值,本文之所以要假设ρ值呈等差数列变化是为了解释中国储蓄率不断上升的趋势。,把模拟值和实际值偏差的绝对值最小的ρ值作为最终选定的值②②该偏差用每年模型模拟值与实际值之差的绝对值加总而得。。经过模拟,发现1978和2013年的ρ值分别取0.3和0.74时符合上述标准,这也符合改革开放以来中国居民所面临的不确定性不断加大的实际情况。得到每一年的ρt值之后就可模拟得到中国储蓄率波动的模拟值,即图4中“带金融加速器”所表示的模型模拟值(记为。

图4 中国储蓄率动态的数值模拟(1978-2013年)
在图4中,比较了“带金融加速器”和“不带金融加速器”两种情况下的中国储蓄率模拟值,其中“不带金融加速器”的模拟值即为图2中由基准模型A给出的理论值。我们发现“带金融加速器”情况下的模拟值能够较好地模拟中国储蓄率实际值的波动情况,主要体现在能够模拟储蓄率实际值不断上升的趋势,因此,带金融加速器的模型能够对中国储蓄率不断上升的特征事实做出很好解释。
为了进一步检验该模型对中国储蓄率的动态模拟,还可以比较中国储蓄率的实际值τt、模型A的模拟值以及模型B的模拟值周期波动成分的共动性。首先对以及等3个时间序列利用HP滤波器进行去趋势操作,从而得到其短期波动周期成分,分别记作和,分别计算这三个时间序列的交叉相关系数及其标准差和相对标准差,结果如表1所示。

表1 中国储蓄率实际值及模拟值的相关性
从表1来看,无论是从同期(即j=0时)的相关性、还是非同期(即j≠0时)的交叉相关性来看,cτt与相关性都比crt与的相关性高,表明模型B比作为基准经济增长模型的模型A更好地拟合了中国储蓄率的短期周期性波动。但从相对标准差来看,的相对标准差更高,表明在随机冲击下中国储蓄率的短期波动性更大。但总体来看,cτt、和的周期波动标准差都不大,说明中国储蓄率在以比较稳定的趋势上升。
五、结 论
本文对于中国“高储蓄率之谜”进行了较为系统的研究。首先应用一个基准的经济增长模型从理论上解释了中国储蓄率偏高的含义,并且度量了偏高的幅度以及偏高的比例,指出中国储蓄率偏高程度正不断上升的事实是中国“高储蓄率之谜”的主要特征。为了解释中国储蓄率的上述特征,本文建立一个扩展的“缓冲存货”模型,分析了存在信贷约束时随机冲击对储蓄率动态的影响机制,指出该机制中存在着金融加速器效应,这种金融加速器效应的存在会放大经济增长率对于储蓄率波动的影响。随后本文应用所建立的模型对中国储蓄率1978年至2013年的波动进行了数值模拟分析,发现在加入不断增强的随机冲击程度后该模型不仅能够较好地解释中国储蓄率不断上升的长期趋势,而且还能够较好地拟合中国储蓄率的短期周期性波动。
本文的分析具有较为明显的政策含义。根据本文的分析,理解“中国高储蓄率之谜”的关键不在于分析某种特定因素是否起到重要作用。中国高储蓄率之所以出现,一方面是因为中国长期以来的高经济增长率,这是中国高储蓄率的决定性因素;另一方面则是改革开放以来中国面临的各种不确定性冲击因素加速了储蓄率的上升。因此,在中国经济维持高增长率的阶段,高储蓄率的长期存在是合理的,但是为了遏制其不断上升的趋势,则有待于逐步完善中国市场经济体制,包括完善各种社会保障体制等,以减少各种不确定性。因此,在促内需以及调整经济结构的过程中,应该正确地看待中国高储蓄率问题,中国的高储蓄率与经济结构失衡等经济现象一样是中国经济长期改革和发展过程中出现的阶段性产物,正确认识这些逻辑关系,有助于实施正确的经济政策,从而最终达到调结构、促转型的目的。
[1] Modigliani F,Cao S.The Chinese Saving Puzzle and the Life-Cycle Hypothesis[J].Journal of Economic Literature,2004(3).
[2] 李文星,徐长生,艾春荣.中国人口年龄结构和居民消费1989-2004[J].经济研究,2008(8).
[3] 汪伟.经济增长、人口结构变化与中国高储蓄[J].经济学(季刊),2009(1).
[4] 李佳峰,刘尧成.中国居民储蓄行为不确定性与外汇储备[J].国际贸易问题,2012(10).
[5] 方丽婷,钱争鸣.社会保障支出与中国居民储蓄[J].统计与信息论坛,2012(10).
[6] 李永友.失衡的增长结构与财政制度安排[J].经济理论与经济管理,2010(9).
[7] 吕冰洋.财政扩张与供需失衡,孰为因?孰为果?[J].经济研究,2011(3).
[8] 林毅夫,姜烨.经济结构、银行业结构与经济发展[J].金融研究,2006(1).
[9] 郭新强,汪伟,杨坤.刚性储蓄、货币政策与中国居民消费动态[J].金融研究,2013(2).
[10]张军.资本形成、工业化与经济增长:中国的转轨特征[J].经济研究,2002(6).
[11]Bernanke B,Gertler M,Gilchrist S.The Financial Accelerator in a Quantitative Business Cycle Framework[J].Handbook of Macroeconomics,1996(1).
