基于二次反射的光学系统聚光特性研究
2015-01-01沈焕波付杰李心李晓波李建华徐能
■ 沈焕波 付杰 李心,2 李晓波 李建华 徐能
(1. 浙江中控太阳能技术有限公司;2. 浙江大学控制科学与工程学系)
0 引言
基于二次反射原理的塔式太阳能光热发电技术是在传统的塔式太阳能热发电技术之上拓展出来的一种聚光太阳能热发电模式。这种发电方式最早于1976年由以色列人Rabl A[1]提出,它来源于卡塞格伦(Cassegrainian)望远镜系统,地面的定日镜镜场组成卡塞格伦系统的主镜,塔上的双曲面作为二次反射的副镜。其与传统的塔式热发电最大的不同在于吸热器的位置,传统塔式热发电一般将吸热器置于支撑塔的顶部,光束下射式热发电系统则通过安装在塔上的一个二次反射面将光能量会聚于离地面很近的吸热器,从而使吸热器的效率得到提高,同时解决了熔盐等导热材料上塔的难题,使系统的安全性能得到了提升。
近年来,随着太阳能热利用研究的深入,国外研究机构对光束下射式热发电系统进行多方论证,尤其是对该系统光学反射系统中光斑的会聚、高温吸热器的研制及二次聚光器件的设计等提出多种可选方案。日本三井造船株式会社通过减少定日镜反射光的遮挡或遮蔽,对二次反射支撑塔进行多种结构设计[2]。美国波音公司结合支撑塔的结构特点设计了一种可移动、机械结构简洁、成本低的塔上二次反射面[3]。以色列威兹曼科学院通过实例模型仿真分析了混合循环模式下的二次反射发电系统[4]。本文主要通过仿真分析双曲二次反射面的光斑特性,得出塔上双曲面的最优化选择。
1 理论基础分析
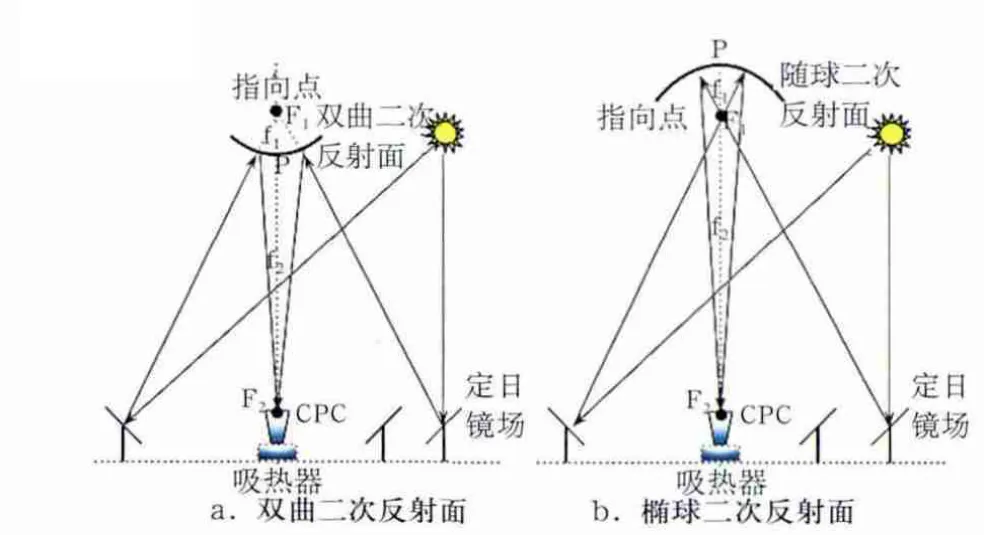
图1 光束下射式太阳能热发电系统
可将塔上汇聚光线反射至地面汇聚点的反射面面型有双曲面及椭球面两种,通过性能对比发现,双曲面面形的实际应用效果明显优于椭球面[5]。两者聚光光路图如图1所示,本文选择双曲二次反射面进行分析。双叶双曲面数学模型如图2所示。
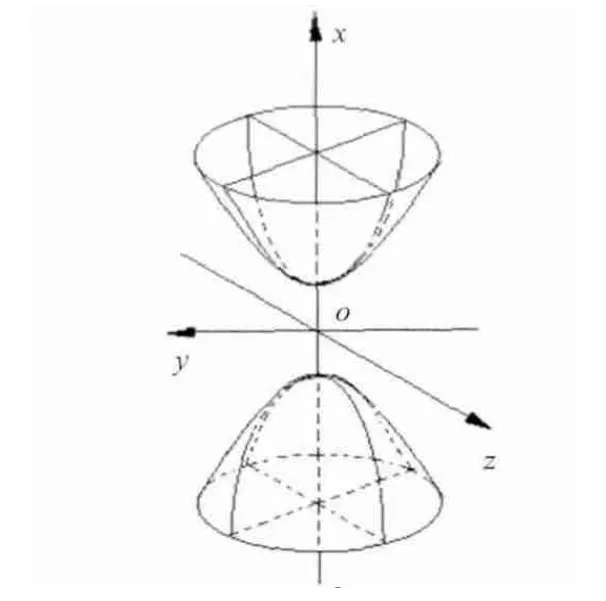
图2 双叶双曲面的一般图形
双叶双曲面的光学特性为过其上焦点的光线必过其下焦点[6-7],利用双曲面该特性,光束下射式热发电系统将定日镜反射的太阳光线对准双曲面上焦点,经双曲面二次反射至位于下焦面位置的吸热器入口,从而巧妙地实现了将塔式光热发电的核心部件如高温熔盐吸热器置于地面,提升了熔盐电站的安全性。
对于塔下用于收集并反射光线的定日镜,太阳光线经其反射的出射光线中,除中心主光线对准双曲面上焦点并二次反射后会聚于下焦点位置外,其余反射光线都有一定离焦量,从而导致吸热面处的光斑存在一定发散性。一般,为保证吸热器表面的光斑有足够的聚光比,往往在吸热器入口位置设置相匹配的复合抛物聚光器(CPC)对塔上二次反射镜反射的光斑进一步聚光,以达到更高聚光比。聚光比越高,工作温度越高,电站的光电转换效率也越高,尤其对于多级太阳能混合循环发电模式,工作温度在1000~1300 ℃,聚光比更是达到几千,通过CPC再聚光后,吸热器表面的能流密度可达到1000 kW/m2以上[8]。
2 光学建模
双曲面的投射光斑放大率可定义为下焦点处光斑面积与定日镜面积的比值大小,根据几何光学的物像放大关系可知,其值应为光学系统中线放大率M的平方[9],下文以线放大率M表述光束下射式热发电系统的聚光特性。在图1中,将双曲面顶点P到上焦点F1的距离定义为f1,P到下焦点F2的距离定义为f2,定日镜中心对准上焦点F1,经双曲面二次反射到吸热器入口面。同一面定日镜对于不同面形的双曲二次反射面,投射在吸热器上的光斑面积大小不同。双曲面的面形可由f2和f1的比值决定,故f2/f1的值不同,定日镜投射到吸热器入口面的线放大率M也不同,从而得到M随f2/f1变化的关系曲线。
图3所示为光学软件仿真的多面定日镜经双曲面反射到吸热器入口的光路图,模型不考虑吸热器前端的复合抛物聚光器(CPC)。为确定双曲反射面的反射特性,选择分析单面定日镜模型对应的单镜光斑。在模型中,分别固定吸热塔的高度或上焦点的高度,选择定日镜规格为2 m2的平面反射镜,计算f2/f1与M之间的关系,通过改变f2/f1的值来改变面形,使其满足f2/f1=1,2,...,9,仿真每个面形下单面定日镜在接收面上的光斑图。
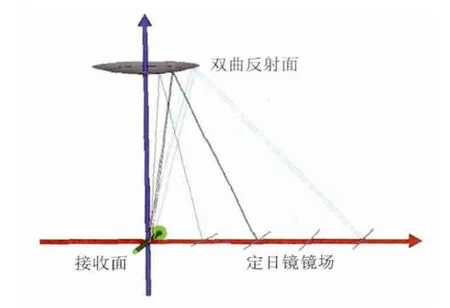
图3 多定日镜反射光路模型
3 光斑特性分析
3.1 塔高固定不变
按照上述方法,首先选定塔高为80 m不变,定日镜离塔距离L为100 m,仿真时刻为夏至日正午12:00,调整单镜模型中双曲面的面形、定日镜的姿态角等参数后,追迹光线得到接收面上各光斑形状如图4所示。为了研究双曲面面形的光学特性,使得单镜光斑的形状和边缘清晰,便于得出双曲面的放大特性,我们一般选用平行光源,故此处不考虑太阳锥角。其中,各光斑的仿真数据及对应的双曲面半径见表1。

图4 f2 /f1取不同值时对应的吸热器入口光斑
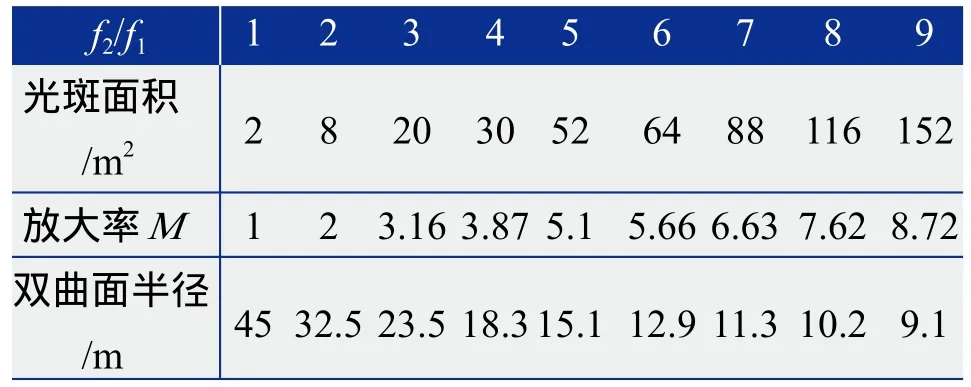
表1 塔高80 m时,系统线放大率M与f2/f1之间的关系
根据表1数据,作线放大率M与f2/f1的折线图,如图5所示。
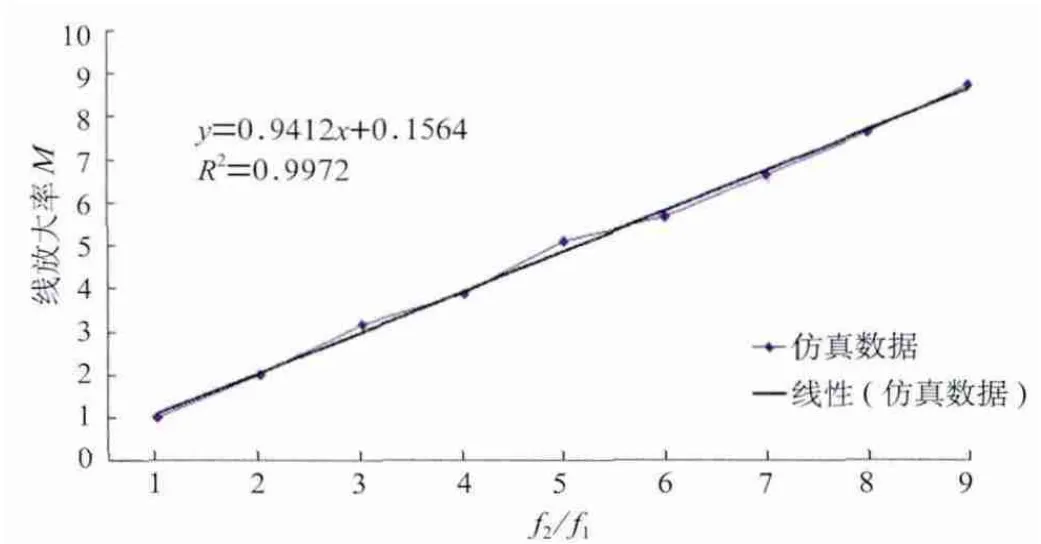
图5 塔高80 m时,光斑线放大率与f2 /f1的关系示意图
由图5可以明显地看出,线放大率M与线性关系式经线性拟合后,得线性拟合方程为:

式(1)拟合直线的决定系数R2为0.9972,说明拟合方程很好地解释了放大率M与f2/f1的关系。列表中,线放大率M和双曲面半径随f2/f1的变化趋势相反,即M随f2/f1的增大而增大,双曲面半径随f2/f1的增大而减小,如图6所示。在电站设计中,我们不仅需要考虑吸热器表面光斑的会聚状况,也要兼顾反射塔上双曲面的尺寸大小。当塔高不变,上焦点越高,即f1越大,镜场内定日镜的阴影遮挡越小,更多光能量将被聚集于吸热器表面,但这也导致了塔上反射镜面积将增大,进而使得支撑塔所需的承重量增加。当f2/f1=4时,光斑线放大率为3.87,双曲面半径为18.3 m,是该情形下较理想的面形设计参数。
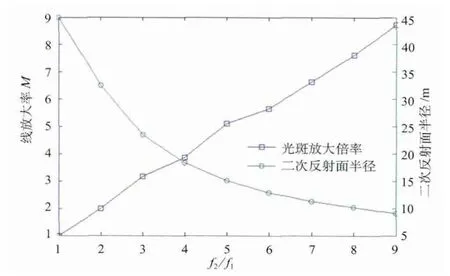
图6 光斑线放大率M、二次反射面半径与f2/f1的关系示意图
3.2 上焦点高度固定
若塔高不固定,上焦点高度为100 m,以离塔100 m的定日镜为例,调整单镜模型中双曲面的面形、定日镜的姿态角等参数后,通过光线追迹,同样可得到一组与图5类似的光斑趋势图。这种情况下,在f2/f1取不同值时对应的光斑大小、线放大率、双曲面半径见表2。
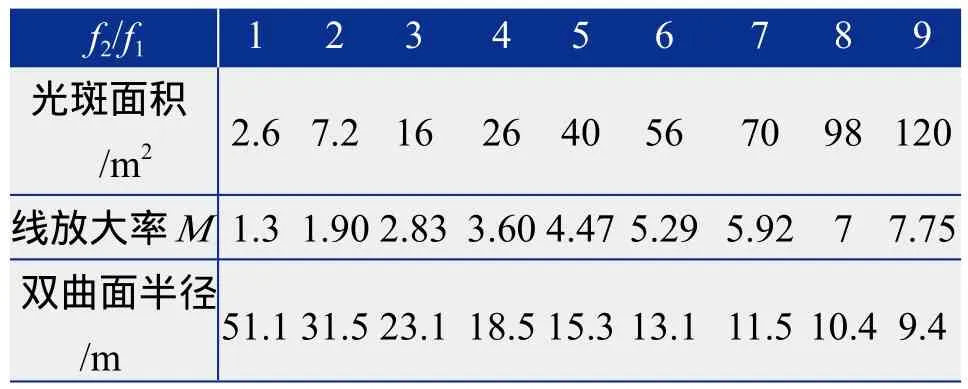
表2 上焦点高100 m时,线放大率M与f2/f1之间的关系
根据表2,作线放大率与f2/f1的折线图,如图7所示,并拟合。
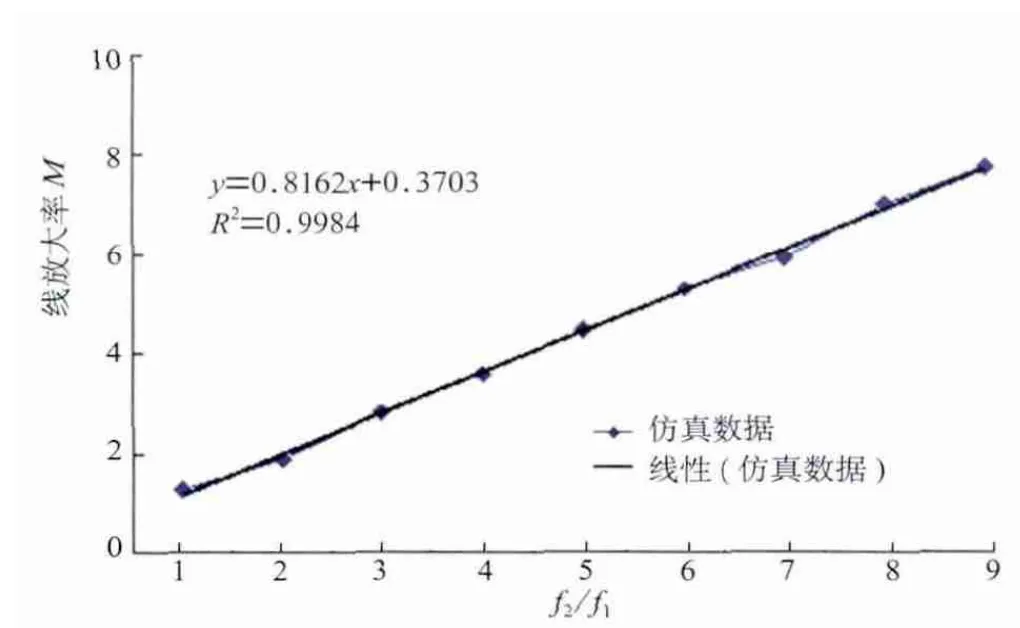
图7 上焦点高度为100 m时,M与f2/f1的关系
由图7可知,放大倍率M与f2/f1也满足线性关系,其拟合方程可表示为:
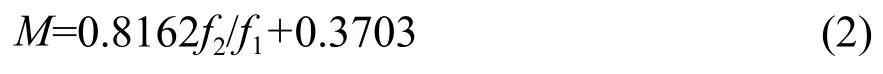
式 (2)拟合直线的决定系数R2为0.9984。对比图5可知,尽管两种情况下的拟合方程不同,但放大率M与f2/f1的关系均满足线性方程。
图8为上焦点高度为100 m时,系统的线放大率M、二次反射面半径与f2/f1的关系曲线。优化的二次反射面形应同时满足尽可能小的反射面半径及线放大率M。从图中两条趋势曲线得出,最佳的f2/f1值应在4附近,光斑线放大率为3.6,双曲面半径为18.5 m。
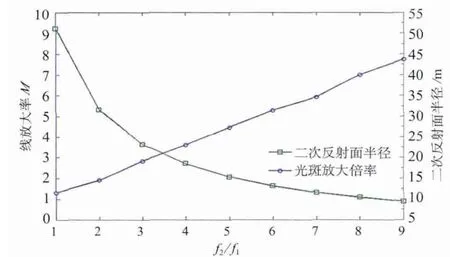
图8 线放大倍率M、半径与f2/f1的关系
在系统设计时,不论先固定塔高,还是先固定上焦点高度,双曲面的线放大率与f2/f1都很好地满足线性关系。综合考虑面形尺寸、光斑放大率、阴影遮挡等因素,一般而言,塔上双曲面的参数f2/f1比较合适的值应在3~5之间。
此外,双曲面面形不同,同一定日镜经其反射的光线与吸热面法线的夹角将不同,即接收角度不同。如图9所示,同样大小的镜场,在上焦点高度不变的情况下,双曲面的曲率半径随f2/f1的减小而增大,双曲面的高度随f2/f1的减小而降低,塔上镜面反射面积越小,吸热器表面的光斑越大,同时,吸热器接收光线的接收角度越大;反之,f2/f1越大,双曲面高度低,对应塔上反射面积越大,吸热器表面光斑越小,吸热器接收的光线角度越大。一般而言,塔上二次反射镜的面积约为定日镜场总反射面积的2%[10]。对于吸热器前端复合抛物聚光器的设计,当接收光线角度越小时,复合抛物聚光器CPC的容忍角度可设计得更小,这样,聚光系统的设计将显得更加方便[11]。
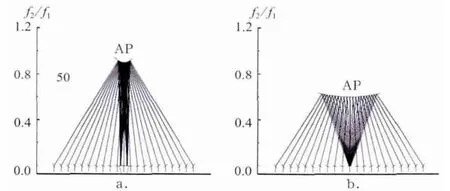
图9 双曲面的光学特性
3.3 离塔不同距离的定日镜仿真
对于单镜模型,固定上焦点高度100 m不变,仿真得到离塔不同距离处定日镜的光斑放大倍率随f2/f1变化的仿真数据见表3。
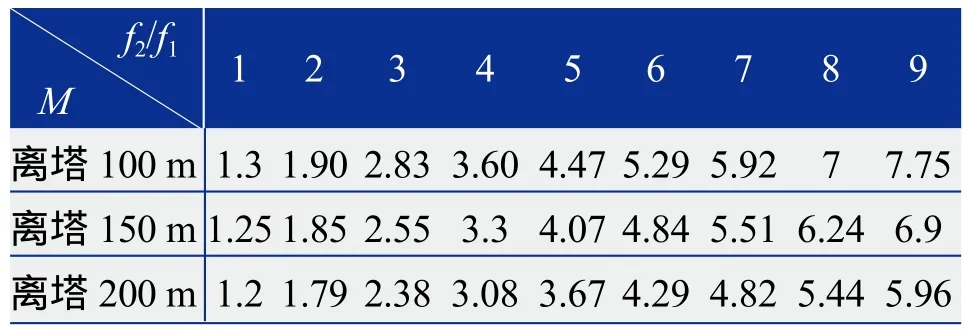
表3 不同距离处的放大倍率与f2/f1的关系
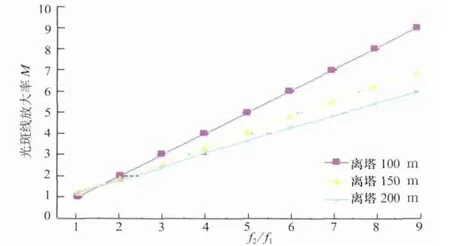
图10 离塔不同距离下,M随f2/f1变化情况
由表3数据作图得到图10,定日镜离塔距离L=100、150、200 m时,其光斑大小随f2/f1变化基本仍满足线性关系,且离塔越远的镜面,光斑的线放大率越小。对于f2/f1取定值的双曲反射面,L越大,塔上反射面所需镜面面积就越大。
4 结论
实际工程应用中,二次反射面形的选择受多种因素影响,主要有双曲面面积的大小、镜场大小、吸热器的尺寸、光线接收角度,以及能流密度的限制等。本文主要从光束下射式热发电系统的基本原理出发,分析了其光路特征,并以塔高80 m和上焦点高度100 m时为例,对光束下射式热发电系统的聚光特性进行深入分析,得出光斑线放大率与双曲面参数f2/f1之间的关系。通过分析不同二次反射面形下的光斑大小,结合双曲面面积大小的限制,着重对塔上二次反射双曲面面形的选择进行分析,得出在光束下射式热发电系统中,最优化的双曲面参数f2/f1应在3~5之间。此外,考虑离塔不同距离下,定日镜光斑的线放大率M随双曲面参数f2/f1的变化,进一步确定M与f2/f1之间的线性关系,同时验证了在其他条件相同的情况下,离塔越远的定日镜,其反射光斑线放大率越小。研究的结论为二次反射热发电系统中塔上反射面面形的设计提供参考依据。
[1] Rabl A. Tower reflector for solar power plant[J]. Solar Energy,1976,18(3): 269 - 171.
[2] 江泽一明,井上浩男,川口隆,等. 光束下射方式太阳光采光装置[P]. 中国: 200880113947.6,2008-10-30.
[3] James B. Blackmon,Brownsboro. Geometric dome stowable tower refl ector[P]. US: 6532953B1,2003-03-18.
[4] Kribus A,Zaibel R,Carey D,et al. A solar-driven combined cycle power plant[J]. Solar Energy,1998,62(2): 121 - 129.
[5] Akiba Segal,Michael Epstein. The optics of the solar tower refl ector[J]. Solar Energy,2000,69: 229- 241.
[6] 张海洪,樊仲维,郝沛明. 两镜系统分析[J]. 量子电子学报,2003,(3): 19 - 23.
[7] 郑世旺. 旋转双曲面成像问题再研究[J]. 河南科学,2003,(3): 17- 20.
[8] Abraham kribus. A high-effi ciency triple cycle for solar power generation[J]. Solar Energy,2002,72(1): 1 - 11.
[9] 李晓彤,岑兆丰. 几何光学·像差·光学设计[M]. 杭州: 浙江大学出版社,2004.
[10] Akiba Segal. Optics of solar concentrators[R].Israel:Weizmann Institute of Science,2010.
[11] Akiba Segal. Optimization of heliostat field layout for the beam-down optics[R]. Israel: Weizmann Institute of Science,2011.
