灰色关联分析在产业发展研究中的应用——以天津软件产业为例
2015-01-01郄红伟朱司宇
◎文/郄红伟 赵 珵 朱司宇
一、产业发展研究的一般视角
产业是经济的主体和支撑,产业发展是经济发展的内容,开展产业发展研究对于实现经济的又好又快发展具有重要意义。
产业研究的内容包含四个方面:一是产业内部各企业之间相互作用关系的规律,二是产业本身的发展规律,三是产业与产业之间互动联系的规律,四是产业在空间区域中的分布规律等。四个方面的研究旨在激发积极因素,遏制不利因素,最终推动产业的发展。作为政府层面的产业发展研究,更多的集中于研究产业发展规律,分析影响产业发展的内部和外部因素,促进产业资源优化布局和最大化利用。
产业发展是指产业的产生、成长和进化过程,既包括单个产业的进化过程,又包括产业总体,即整个国民经济的进化过程。而进化过程既包括某一产业中企业数量、产品或者服务产量等数量上的变化,也包括产业结构的调整、变化、更替和产业主导位置等质量上的变化,而且主要以结构变化为核心,以产业结构优化为发展方向。因此,产业发展包括量的增加和质的飞跃,包括绝对的增长和相对的增长。
当前产业发展研究的方法一是基于资料的定性分析,二是基于各类数据的简单统计分析,三是利用各种科学计量方法分析产业发展影响因素和发展规律,预测产业未来发展规模。本论文主要讨论灰色关联分析方法在产业发展影响因素分析中的应用。
二、灰色关联分析基本概述
(一)灰色系统与灰色关联分析
灰色系统理论是20世纪80年代,由中国华中理工大学邓聚龙教授首先提出并创立的一门新兴学科,它是基于数学理论的系统工程学科。灰色系统理论以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。
灰色关联分析是灰色系统理论的重要组成部分之一,是通过灰色关联度来分析和确定系统中各因素之间的影响程度或因素对系统主行为的贡献程度的一种方法。关联度是事物之间、因素之间关联性的“度量”,它通过从随机性的序列中找到关联性,从而为因素分析、预测的精度分析提供依据,为决策提供基础。
(二)灰色关联分析与统计分析方法的区别
数理统计中的回归分析、方差分析、主成分分析等都是用来进行系统分析的方法,但这些方法要求必须具备大量数据,如果数据量少就难以找出统计规律;要求各因素数据与系统特征数据之间呈线性关系并且彼此无关;要求样本数据服从某个典型的概率分布。但是在实际工作中,这种要求往往难以满足,尤其是在我国统计数据比较有限,而且现有数据灰度较大的情况下,许多数据难以找到典型的分布规律。往往计算量大、过程复杂,常需要借助计算软件,可能出现量化结果与定性分析结果不符的现象,导致系统的关系和规律遭到歪曲和颠倒。
灰色关联分析从某种程度上弥补了上述缺憾,它对样本量的多少和样本有无规律都同样适用,而且计算量小,分析的结果一般与定性分析相吻合。因此,灰色关联分析是系统分析中很有独特优势、比较实用和可到的分析方法。
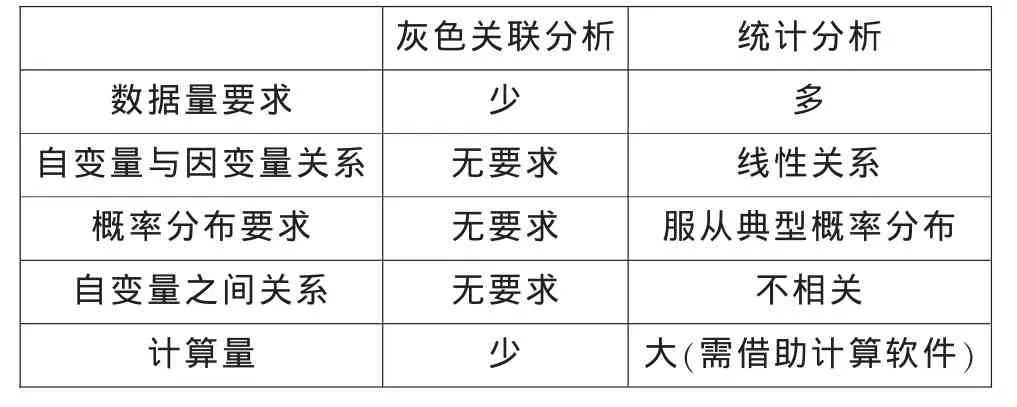
表1 灰色关联分析与统计分析方法的区别
(三)灰色关联分析的应用流程和方法
进行灰色关联分析从大的方面一般需要四个流程:一是建立指标体系,二是生成灰色序列,三是计算灰色关联度,四是基于计算结果并结合实际情况对结果进行分析,提出对策。
1.建立指标体系
指标体系的建立是为了更好地测度哪些因素对产业发展影响较大,为相关决策提供现实量化的依据,指标的选择主要基于以下原则:
客观性原则。指标体系的建立应结合产业实际和经济发展水平,并且体系建立之后的实证研究也必须遵循这一原则,在搜集数据的过程中尽量采用原始数据,数据源应权威可靠。
可操作性原则。设计的指标数据应容易获得,进而能够科学地应用于评价实际,发挥其应有的评价功能。同时指标应具有比较性和可测性,计算方法容易掌握,这样才能有其现实的意义。
系统性原则。指标体系的建立要处理好部分与整体、具体行动与系统目标之间的关系。作为一个有机整体不但应从各个层次、各个角度反映被评价对象的特征和状况,而且还要体现对象的变化趋势,反映对象的发展动态。
代表性原则。由于影响产业发展的因素很多,作为系统化的指标体系,要在众多可用指标中筛选最具代表性、最灵敏的主导性指标。
2.生成灰色序列
对一个抽象的系统或现象进行分析,首先要选准反映系统行为特征的数据序列。例如,用国民平均接受教育的年数来反映教育发达程度,用刑事案件的发案率来反映社会治安面貌和社会秩序,用医院挂号次数来反映国民的健康水平等。有了系统行为特征数据和相关因素的数据,即可做出各个序列的图形,从直观上进行分析。
因为灰色关联分析是通过对少量的原始数据进行分析来寻求规律,而这少量的原始数据具有一定的随机性。因此,应该通过某种生成方法来弱化其随机性,显示其规律性。缓冲算子是对原始数据进行处理的一种方法,缓冲算子包括两类,一是弱化缓冲算子,二是强化缓冲算子。
(1)弱化缓冲算子。设为系统行为数据系列,为缓冲算子,当分别为单调增长序列,单调衰减序列或者震荡序列时,缓冲序列比行为序列的增长速度(或衰减速度)减缓或振幅减小,称缓冲算子为弱化缓冲算子。
生成灰色序列需要结合对原始数据的分析以及环境的考虑,如果原始数据增长或衰减较快,明显高于正常增速(减速),则需要弱化序列的增长(衰减)趋势。如,产业发展之初由于基数较小,加之政策的扶持,增速较快;但是随着产业的日渐成熟,规模的扩大,相应的扶持政策也将弱化,在大的基数上实现较快增长也很困难,因此增速势必会下降。
当前较为广泛使用的弱化缓冲算子计算方法主要有:平均弱化缓冲算子、几何平均弱化缓冲算子、加权平均弱化缓冲算子、加权几何平均弱化缓冲算子。一些学者在此基础上对弱化缓冲算子进行了扩展研究。各种弱化缓冲算子均有一定的计算模型,可参考文献[1],在此不再赘述。
如果要降低弱化速度,可以使用加权几何平均弱化缓冲算子;如果要提高弱化速度,可以使用加权平均弱化缓冲算子;在同一类算子中,可通过变化不同时期数据的权重适当调整弱化速度。
(2)强化缓冲算子。设为系统行为数据系列,为缓冲算子,当分别为单调增长序列,单调衰减序列或者震荡序列时,缓冲序列比行为序列的增长速度(或衰减速度)加快或振幅增大,称缓冲算子为强化缓冲算子。
如果原始数据增长(衰减)较慢,明显低于正常增速(减速),则需要强化序列的增长(衰减)趋势。如,受金融危机的影响,从2008年开始,很多产业增速甚至规模出现下滑,如果以这一时段的数据寻求产业发展规律,势必会出现偏颇。因此,应强化原始数据的增长趋势。
当前较为广泛使用的强化缓冲算子计算方法主要有:平均强化缓冲算子、几何平均强化缓冲算子、加权平均强化缓冲算子、加权几何平均强化缓冲算子。一些学者在此基础上对强化缓冲算子进行了扩展研究。各种强化缓冲算子均有一定的计算模型,可参考文献[2],在此不再赘述。
如果要使强化速度快一些,可使用加权几何平均强化算子;如果想使强化速度慢一些,可使用加权平均强化缓冲算子;在同一类算子中,还可以通过调整各时期数据的权重改变强化速度。
当然,如果数据未出现增长(衰减)较快(较慢)的情况,能够代表产业发展趋势,可以不利用上述方法生成序列。此外,在搜集数据时,常常由于一些不易克服的困难导致数据序列出现空缺,也有些数据序列虽然完整,但由于系统行为在某个时点上发生突变而形成异常数据,这时如果剔除异常数据就会留下空穴,面对这种情况可以利用均值生成算子。
3.计算灰色关联度
如果各因素具有不同的量纲,计算灰色关联度之前应首先对序列数据进行无量纲化处理,使得数据能够横向对比。当前无量纲化处理的方法主要有初值化生成、均值化生成、区间生成、逆化生成和倒数化生成。
从现有的研究来看,判断因素数据序列间关联度的方法主要有:邓氏关联度、绝对关联度、相对关联度、斜率关联度、T型关联度、C型关联度、改进的关联度等典型方法,此外,还有众多学者对上述计算方法进行了改进,形成许多新的改进模型。这些方法大致可以分为三类:一类是强调序列的绝对位置差,如邓氏关联度、灰色绝对关联度、T型关联度等;一类是强调序列的变化率,如B型关联度、斜率关联度等;此外,还有一些关联度的构造建立在上述两角度的基础之上,即考虑绝对变化,又考虑相对变化。
关联度计算方法的选择应基于以下三个原则:(1)优先选取即涵盖绝对位置差又涵盖变化率的灰色关联度算法模型,这也是一种未来研究的趋势。(2)优先考虑保序性,保序性即无论是否进行无量纲化处理以及采用何种无量纲化处理方法(初值化、均值化、标准化等)均不会影响各因素的关联度大小。(3)结合定性分析,在应用灰色关联分析方法之前,一定要进行相应的定性分析,确认所研究的问题满足或适合灰关联分析的应用前提和条件。否则,研究结论的可靠性会遭到怀疑。
4.计算结果分析
利用上面的各个模型计算出来的灰色关联度的大小是衡量序列之间紧密程度的一种尺度,而在进行系统分析时,研究系统特征行为与因素行为之间的关系,应关注的重点是系统特征行为序列和各个因素行为序列关联度大小的顺序,而不完全是关注度在数值上的大小。同时也要结合产业的发展实际以及内外部环境对评价结果进行验证,在关联度排序靠前的因素对系统特征行为的影响较大,反之较小。最后要根据各因素影响力的大小提出相应的对策建议。
三、灰色关联分析在天津软件产业发展研究中的应用
(一)天津软件产业发展灰色关联分析
1.指标选取
基于指标体系建立原则,本文选取了软件业务收入X1、纳入统计的软件企业数Y1(代表企业规模)、软件业务收入过亿元企业Y2(代表企业质量)、登记软件产品数量Y3(代表产品质量)、软件从业人员Y4(代表人员规模)、研发经费投入Y5(代表创新投入)、嵌入式软件所占比重Y6(代表产业结构)。以软件业务收入为母因素,其余指标为子因素,分析各子因素对软件业务收入的影响。
2.生成灰色序列
计算原始数据的增长速度(见表2)。由表可见,纳入统计的软件企业数在2009年、2011年和2012年有一定的突变,软件业务收入过亿元企业在2009年出现突变,因此,采用紧邻均值生成序列;研发经费变化不定,增长和降低速度均较快,因此,采用平均弱化缓冲算子进行计算。计算结果见表3。
3.计算灰色关联度
(1)无量纲化处理。因为选取的指标量纲不同,为便于比较,对表3中的数据进行无量纲化处理,本文选取均值化生成(见表4)。
(2)计算灰色关联度。本部分利用孙玉刚在《灰色关联分析及其应用的研究》中改进的灰色斜率关联度算法进行计算,因为该算法具有规范性、保序性、对称性、唯一性、可比性,并且能够体现关联度的正负性问题。计算公式为:
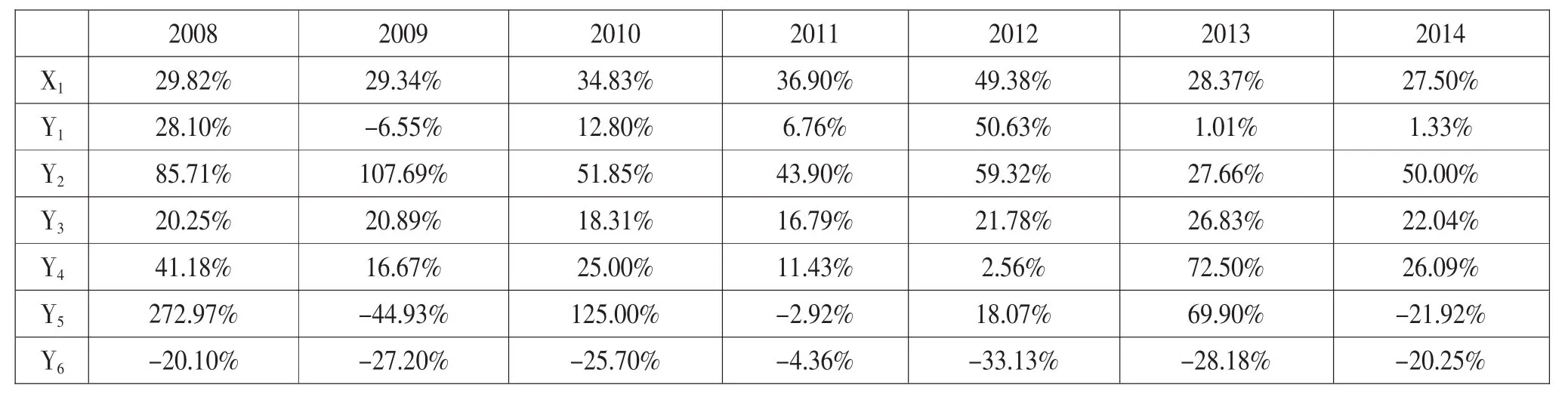
表2 原始数据的同比增长率

表3 均值生成后的序列算子
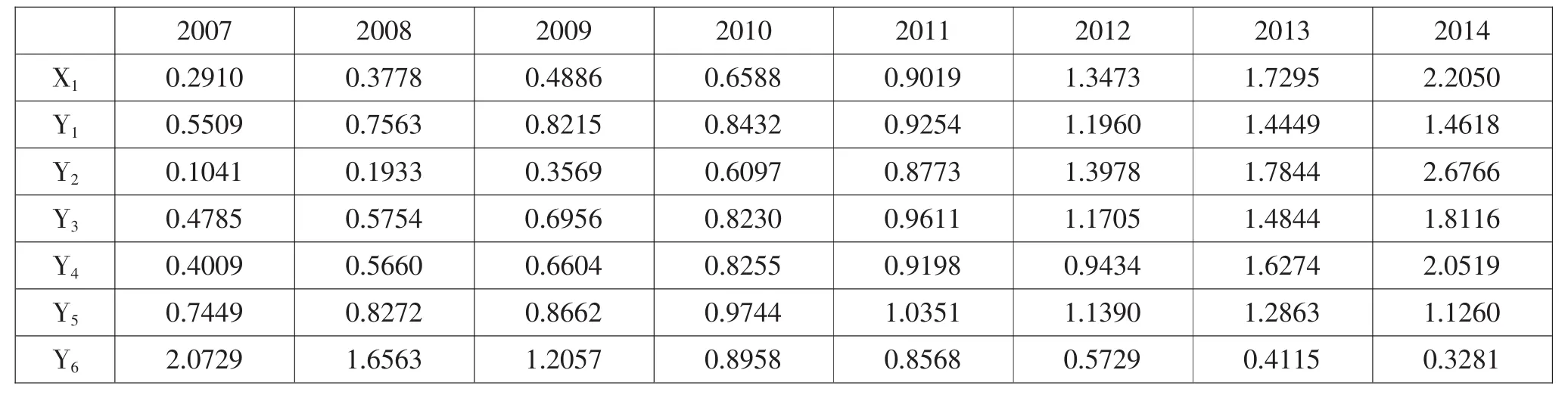
表4 无量钢化后的序列算子

根据上述公式进行计算得到各因素与软件业务收入的关联度,见表5。

表5 灰色关联度计算结果
对计算结果进行排序,即软件业务收入过亿元企业的数量对产业发展的影响最大,其次是软件从业人员,之后是研发经费投入、登记软件产品数量、纳入统计的软件企业数量,而嵌入式软件所占的比重与产业发展负相关。
(二)天津软件产业发展对策
根据上述计算结果可以提出如下发展对策。
1.着力发展壮大规模型软件企业
规模型企业尤其是龙头企业对于产业发展的贡献度较大,一方面应瞄准全球软件五百强和中国软件百强企业,加大招商引资力度;另一方面,应加大对本土软件企业的扶持力度,通过项目扶持、政府采购等方式,鼓励企业做大做强;此外,还要鼓励企业合并、重组,充分集成多方优势,培育企业实力、壮大企业规模。
2.着力壮大软件人才队伍
多年来,软件人才总量不足、高端软件人才缺乏一直是制约天津软件产业发展的一个瓶颈,由于毗邻北京加之工资水平较低,很多软件人才都流失到北京、上海等城市。
今后应发挥好天津市大学软件园的作用,加大软件人才培养力度;要加强对现有软件人才的培训力度;要借助近几年天津经济发展较快,而消费相对较低的比较优势,留住现有人才,同时吸引一批高端人才。
3.鼓励企业加大研发投入
从全国范围来看,我国软件产业起步较晚,大部分软件产品被外国垄断,软件服务外包长期以来在产业中占有很大比重,因此企业普遍对研发经费的投入不重视。而要真正能够培育出具有市场竞争力的软件产品,打破国外的垄断,必需发挥企业的主体作用,加强产学研联合攻关,建立多元化投入体系,加大研发投入。
4.着力培育一批具有竞争力的软件产品
软件产品在软件业务收入中所占的比重是衡量产业结构的一重要指标,而同时,一个具有竞争力的软件产品能够带动企业快速占领市场,带动产业规模迅速扩大。近几年天津的这一比重虽有提高,但总体还较低。因此,应加大扶持力度,鼓励企业开发或产学研联合开发一批具有竞争力的软件产品。
5.做大软件企业的群体规模
要把握当前科技型中小企业蓬勃发展的战略机遇,加大政策宣传力度,鼓励各类科技人员创办领班软件企业;同时鼓励其他行业内设的信息部门、软件部门独立,成立独立的软件公司,享受国务院关于进一步鼓励软件和集成电路产业发展的相关政策。通过企业群体规模的扩大,带动产业规模的扩大。
6.进一步缩小嵌入式软件比重
嵌入式软件所占的比重与软件产业发展负相关,主要是由于我国对嵌入式软件的统计采用制造业收入乘以一定的比重,嵌入式软件一直是低端的代表。近年来,天津不断加大软件产业结构的调整,嵌入式软件所占的比重逐年下降,但是仍高于全国平均水平,还应进一步加大调整力度。
[1]党耀国,刘思峰,刘斌,唐学文.关于弱化缓冲算子的研究[J].中国管理科学,2004(2):108-111.
[2]党耀国,刘斌,关叶青.关于强化缓冲算子的研究[J].控制与决策,2005(12):1332-1336.
[3]党耀国,刘思峰,王正新,林益.灰色预测与决策模型研究[M].北京:科学出版社,2009:64-65.
[4]田民 ,刘思峰,卜志坤.灰色关联度算法模型的研究综述[J].统计与决策,2008(1):24-27.
[5]孙玉刚.灰色关联分析及其应用的研究[D].南京:南京航空航天大学硕士论文,2007.
[6]曹明霞.灰色关联分析模型及其应用的研究[D].南京:南京航空航天大学硕士论文,2007.
