ADAMS仿真软件在多管火箭炮定向管中的应用
2014-12-31赵韶斌
赵韶斌,杨 臻,刘 佳
(1.中北大学 机电工程学院,山西 太原 030051;2.中国人民解放军第6904工厂,山西 太原 030006)
多管火箭武器作为现代战争中的压制性武器,具有射程远、威力大、机动性好、反应快等优点,但是多管火箭武器的射击精度限制了它的应用范围。火箭弹在发射阶段的精度受两部分因素的影响,即初始扰动和飞行扰动[1]。初始扰动不仅与火箭弹本身有关,也与发射系统有关。对于发射系统来说,火箭炮定向管的壁厚也是影响火箭弹初始扰动的一个因素。因此建立正确的物理模型,以此来研究和讨论多管火箭武器在不同定向管壁厚下火箭弹的初始扰动情况是一件很有意义的工作,能对火箭炮的结构优化设计提供依据。
1 初始扰动计算的理论基础
火箭弹发射过程中,定向管与其直接接触,因此,想要研究整个发射装置的振动对火箭弹初始扰动的影响,只需研究火箭弹出炮口时定向管的振动对火箭弹初始扰动的影响即可[2]。
图1为火箭弹出定向管口时的示意图。oxy是静坐标系,x轴为定向管静态时的轴线,与水平轴X的夹角为θ(即高低射角);RyHxH为动坐标系,点R为火箭弹后定心部的质心,点O′为火箭弹的质心。轴x1为定向管的轴线,轴为火箭弹的轴线,lR为火箭弹质心到火箭弹后定心部的距离,lB为火箭弹前后定心部之间的距离。作如下假设[3]:①定向管轴线x1的角位移为β,M点的x坐标xM近似为常数;②不考虑弹管间隙和定向管微弯曲的影响,在半约束期开始瞬间(t=tf)弹轴x′1与轴x1重合且有相同的角速度,直到半约束期结束(t=t0)火箭弹后定心部质心R始终位于轴x1上。则点R的y轴坐标为:

其中:yR与xR分别为点R的y坐标与x坐标;yM与xM分别为点M的y坐标与x坐标。
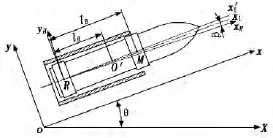
图1 火箭弹出定向管口时的示意图
将式(1)对时间求导可得R点的纵向速度与纵向加速度:
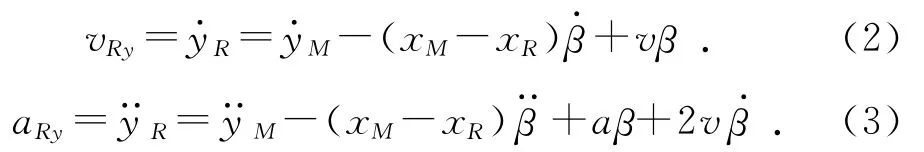
其中:v为火箭弹前定心部质心与后定心部质心相对于动坐标系水平方向的速度;a为火箭弹前定心部质心与后定心部质心相对于动坐标系水平方向的加速度。
在tf到t0时间内,对高低平面内弹轴摆动微分方程IR=-mlRaRy(其中,IR为火箭弹相对于弹轴质心的惯性矩为火箭弹跳动角加速度,m为火箭弹的质量)积分可得到火箭弹在半约束期内高低平面内的初始扰动:
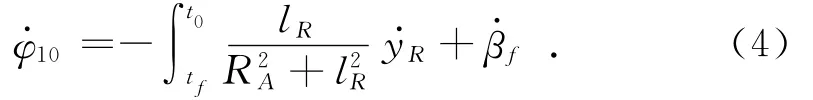
其中:RA为火箭弹的赤道回转半径;为火箭弹前定心部出定向管口时定向管高低方向上的角速度。
将式(2)代入式(4)并化简,最终得到高低方向初始扰动的具体表达式为:
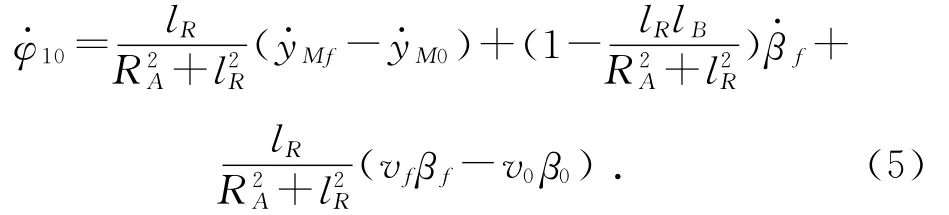
2 动力学模型
2.1 模型的简化[4]
由于多管火箭炮结构复杂,直接在ADAMS中建立动力学模型比较困难,因此先在SolidWorks中建立模型,然后保存为x_t格式的文件,再导入ADAMS中。图2为导入ADAMS中添加完各种约束条件的多管火箭炮动力学模型。

图2 多管火箭炮动力学模型
多管火箭武器是复杂的机械系统,系统的各部件在发射时都会产生相应的运动,对多管火箭武器进行发射动力学分析,必须对整个系统进行合理的简化,直接用多体动力学软件建立完整的仿真模型是不现实的。通过合理的简化后该模型主要包括左右箱体、转塔、底座3大部分。其中,左右箱体靠转轴与转塔联接,左右箱体又包括定向管、前隔板、中隔板、后隔板、蒙皮、侧板和火箭弹等,转塔包括高低机与方向机等。各部分约束关系如下:①假设底座固定不动,用固定副与地面联接;②起落部分和转塔之间有相对转动的运动关系,可以用旋转副来模拟,同时在旋转副上施加具有结构阻尼的扭簧来等效高低机的柔性效应;③转塔与底座之间有相对转动的运动关系,可以用旋转副来模拟,同时在旋转副上施加具有结构阻尼的扭簧来等效方向机的柔性效应。
2.2 外部激励的施加
火箭发动机工作时不断喷出燃气作功,为火箭弹提供动力。燃料的不断燃烧导致火箭弹的质量减少,但是在定向管内的工作时间极短,故而忽略质量的变化。整个动力学仿真过程中,火箭发动机推力经过5 ms后达到稳定推力,发动机工作时间(约为0.8s)远大于火箭弹在定向管内的运动时间(约为0.064s),稳定推力为10.8kN,发动机工作0.8s后推力降为0 N。某发火箭弹发动机的推力函数表达式为:IF(TIME:0,0,IF(TIME-0.8:AKISPL(TIME,0,SPLINE_1,0),0,0)),发动机推力—时间曲线如图3所示。火箭弹与定向管之间的碰撞与摩擦用ADAMS中的IMRACT接触碰撞模型模拟。

图3 发动机推力—时间曲线
3 动力学计算结果分析
模型建立完毕后,根据相关资料和以往的设计经验,分别计算了火箭炮定向管壁厚为2.2mm,2.4 mm,2.6mm,2.8mm,3.0mm,3.2mm,3.5mm这7种情况下模型的动态响应结果。图4~图7为定向管壁厚为2.2mm时的动态响应曲线。
图4 定向管口高低方向线速度曲线
在ADAMS中能够方便地测出tf=0.038 4s,t0=0.053s,这样通过图4~图7得到的曲线就可以计算出火箭弹在高低方向上的初始扰动φ·10以及火箭弹在水平方向上的初始扰动φ·20。表1为计算得到的不同壁厚下的各扰动值。
图5 定向管口水平方向线速度曲线

图6 定向管口高低方向角速度曲线

图7 定向管口水平方向角速度曲线

表1 定向管不同壁厚下的各扰动值
为了更加直观地比较各种情况下的φ·10与φ·20,将表1中的值绘制成曲线,如图8所示。
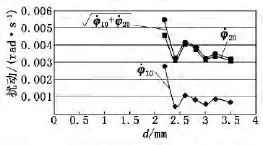
图8 定向管不同壁厚下的扰动值曲线
通过对表1和图8的分析可知:①火箭弹在水平方向上的起始扰动要大于在高低方向上的起始扰动;②φ与的值在定向管壁厚为2.4mm时最小,且它们的综合效应也是在壁厚为2.4mm时最小。由此可以得到,当火箭炮定向管壁厚为2.4mm时,火箭弹发射时起始扰动最小,这一数值是较为合理的定向管壁厚值。
4 结论
通过分析计算与对比,发现火箭弹的初始扰动会随定向管壁厚的变化而变化。所以,确定一个合理的壁厚值是非常有意义的,在本模型中,当定向管壁厚为2.4mm时,火箭弹的初始扰动值最小。
[1]姚昌仁,唐国梁.火箭导弹发射动力学[M].北京:北京理工大学出版社,1996.
[2]赵岗,马大为.基于起始扰动仿真的火箭炮动力因素匹配研究[J].计算机工程与设计,2007(1):43-47.
[3]贺北斗,林永明.火箭发射装置设计[M].北京:国防工业出版社,1988.
[4]郑建荣.ADAMS虚拟样机技术入门与提高[M].北京:机械工业出版社,2002.
