Parameter Identification of Thermal Visco-plastic Model for Magnesium Alloy AZ31D

JIN Quan-lin，ZHANG Yan-shu

（Adevanced Manufacture Technology Center，China Academy Machinery Science＆ Technology，Beijing 100083，China）

1 Introduction

The magnesium alloy is a structure material which is applied widely for different mechanical sand electrical productions because of its higher ration of strength and density.The hot plastic forming is very important technology for manufacturing magnesium parts，therefore the research on numerical simulation of hot plastic forming process and prediction of the microstructure evolution have important significance to improve the performance of magnesium alloy products.A lot of numerical simulation results show that the constitutive relation and the constitutive parameters，which used for numerical calculation，have significant influence on the simulated results，specially the predicted microstructure results.Traditional method of measuring the material parameters is compression test and metallurgical observation of the deformed specimen and the data treatment by the volume average or area average method.However the treated data is not proper for numerical simulation of microstructure evolution because the specimen size is much larger than the grain size.For this reason，the parameter identification for magnesium alloy is the emphasis in this paper.

In order to realize prediction of microstructure during hot working，a thermal visco-plastic model considering dynamic recrystallization（VPDR）is developed firstly by Jin［1］and then improved by Qu et al recently［2］.The constitutive model includes more material parameters.It is very difficult to measure these parameters accurately by means of the existing conventional testing method because of complexity of the hot forging process.The inverse analysis technique may be a way to solve the problem.Its principle is to optimize the material parameters for minimizing a particular norm of the difference between the calculated values and the experimental results.

As well know the classical local optimization methods based on local differential［3—4］may be failing for the complex problem with non-convex objective function，so the global optimization algorithm has to be developed.The global algorithm includes both determinate approach and stochastic approach.The existing determinate algorithms use some mathematic characters of objective function，so its application is limited.The stochastic approach is a global search method.Most of them are based on evolutionary strategies mainly，such as the shuffled complex evolution method［5］，the real-coded genetic algorithm［6］.Considering slower convergence of the stochastic algorithm，most researchers think that only hybrid algorithms can lead to really interesting performance.

A hybrid evolutionary method is constructed to identify the parameters of VPDR in this paper.The algorithm includes the genetic algorithm with multiple crossover operators and L-M algorithm.A special numerical program for parameter identification of VPDR has been made through combination of above hybrid algorithm and a 2D program for simulating hot forging processing.

A set of satisfactory material parameters for AZ31D magnesium alloy is obtained respectively by the proposed inverse analysis numerical procedure.The set material parameters is validated through back extrusion experiment of a magnesium alloy AZ31D part and its numerical simulation.In any case，the parameter identification for macro-micro coupled hot plastic constitutive relation is very complex and difficult project［11—12］，where are many problems on theory and algorithm to be studied.

2 Thermal visco-plastic model

The VPDR is developed firstly by Jin［1］，and improved by Qu and et al.［2］recently.This model emphasizes dynamic recrystalllization evolution and its coupling with macroscopic deformation through dividing the recrystallized region and un-recrystallized region.In the model the microstructure evolution is described by the volume fraction of recrystallizationX，un-recrystallized grain sizeD1，recrystallized grain sizeD2，the average grain sizeDand the maximum difference of grain sizeDdis，where the subscript 1 and 2 denotes the variable in the unrecrystallized region and in the recrystallized region，respectively.In the model there are 19 material parameters to be identified:A1，A2，C1，C2，P1，P2，Q，n，M0，QM，aγ0，F10，F20，QF，li/ld，C，P，β0，Qβ.

3 Objective function

Objective function.Set the parameter vector K，upper limit vector U and lower limit vector L.

The objective function can be expressed as:

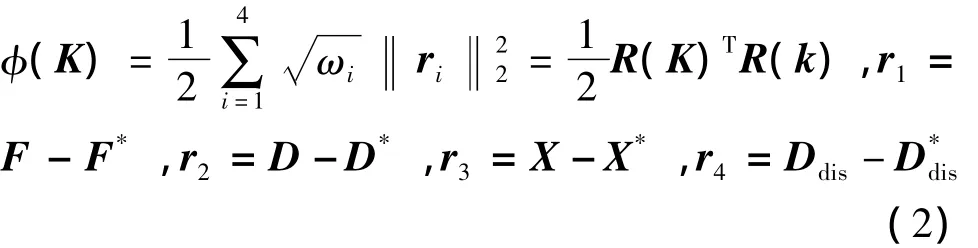
Where ωi（i=1，2，3，4）are the weights of residual vector ri（i=1，2，3，4）.In above equations，F*represents measured loads at different time points，X*，D*，represent the measured values of the recrystallized volume fractions，the average grain sizes and the maximum grain size differences.F，X，D，Didsare the related calculated values.Let ω1=1 and ω2，ω3，ω4can be determined by the relative magnitude of ri（i=1，2，3，4）.

Calculation of objective function.The experimental results in this paper are from the compression test of cylindrical specimen under constant temperature and constant velocity［7］.The experimental results include the load-displacement curve，distribution of average grain size，volume fraction of dynamic recrystallization，and maximum difference of grain size.The related calculated results are from numerical simulation of the upsetting test by using a special version of 2D rigid-plastic finite element program with the VPDR model.

高中地理教材中穿插着许多地理图表，可以分为分布图、示意图、景观图、漫画等，具有很强的直观性，有助于学生对知识的掌握，这是地理教材改革的重要举措，也是培养学生技能的很好平台。教材大幅度精简了陈述性的知识，大量运用插图与学生心理紧密联系，激发学生的学习兴趣，真正体现了新课程标准对“知识与技能、过程与方法、情感态度与价值观”的要求。

Characteristics of objective function.A lot of numerical calculation show that the objective function has the following characteristics:（1）The objective function is non-convex.（2）The parameter space for numerically feasible solution is not clear.（3）Huge compute resource may be need for calculating the objective function.（4）The parameter sensitivity of the objective function is poor.

4 Global optimization agorithm

Considering above characters of the objective function，a hybrid evolutionary method（HEM）is designed.This is a global optimization strategy，which is a combination of the genetic algorithm（GA）［6］，Levenberg-Marquardt（L-M）algorithm［3］，augmented Gauss-Newton（NL2SNO）algorithm［4］with the flexible tolerance method［8］and the concept of complex［9］.Because of its global search ability and slower convergence，GA in HEM is only for finding a good initial value of the solution，and then using L-M algorithm and NL2SNO refine gradually the obtained the solution.When the solution obtained by L-M algorithm and NL2SNO algorithm is numerically infeasible，the flexible tolerance method is used in order to find a numerically feasible solution to replace the numerically infeasible solution.The solution obtained by NL2SNO algorithm as a child of GA population turn to GA until the stop criterion is reached.

Real-coded genetic algorithm（RGA）.As a global optimization technique，RGA includes production operator，crossover operator and mutation operator.Here a real number vector（parameter vector）is regarded as a representation of problem.

Generation of initial population.Considering variation interval of some parameters may be very large the method of population initialization is as follows.

Mutation operator.No-uniform mutation operator（Herrera et al.，1998）is a successful mutation operator，which makes a uniform search in the population at initial stage and very locally at a later stage.However the value from operator is biased towards the points with larger absolute value.In order to make the mutation operator search parameter space thoroughly as possible，the following hybrid no-uniform mutation operator is proposed.

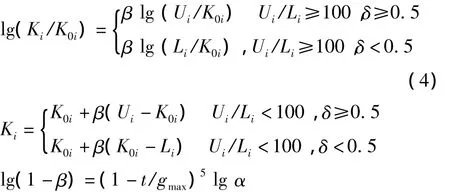
In above equations，K0iis the gene of parent，tandgmaxis the current generation number and set maximum generation number respectively.

Crossover operator.The crossover operator is the core of genetic algorithm.The above method used for the initial population and the mutation operator is also applied to the crossover operator.

Considering advantages of different crossover operators，a hybrid crossover operator is designed.The hybrid crossover operator combines SBX crossover operator，Random simplex crossover operator，FCB crossover operator，arithmetical crossover operator with one dimensional golden section local search algorithm.By using the concept of complex shuffling，several parents are selected from populationPas a complexA，and then the crossover operator and mutation operator are applied in a complex;the generated children fromAare shuffled inPat last.

Generation-alteration model（GAM）.GAM determines how to choose pairs of parents for generating children by the crossover operators and the mutation operators and how to select parents surviving in the next generation.Here GAM role is to search thoroughly parameter space，because GA is used only for finding a good initial solution of classic optimization method.After arrayingNchromosomes in order of decreasing objective function，the selection probability of chromosomeiis as:

Classic optimization method.Classic local optimization method is based on the following quadratic Taylor expansion of objective function φ（K）at Kt.

Where Rt=R（Kt），Jt= ▽Rt，H=J+Rt▽2Rt.The OnlyJtis considered in L-M algorithm based on Gauss-Newton model（Kt+1）and the trust region technology.However，the error due to ignoring Rt▽2Rtmay be larger because of nonlinear interaction among parameters and large residuals Rt.NL2SNO based on augmented Gauss-Newton model（Kt+1）is just for dealing with the case because of including Rt▽2Rt.On other hand，more tests show that predicted φ（Kt+1）by（Kt+1）is often better than that by（K）for small time steps.For this reason，the Lt+1-M algorithm is first is started up to refine the initial solution from GA until ΔKtis enough small.After this，NL2SNO algorithm runs to make a last few refining iteration.When some solutions given by L-M and NL2SNO may be numerically infeasible，the feasible tolerance method is adopted for producing a numerically feasible solution.The feasible tolerance method is not only able to avoid that the iteration process is trapped by minor optimum but also in dependent on derivative of objective function.

In L-M algorithm a set of constraints is added into the objective function by weighted penalty function.Let denote the solution obtained by L-M algorithm，then the set of constraints is:if＜LithenKi=Li，ifLi＜＜Ui，thenKi=，if＞Ui，thenKi=Ui.

Feasibility enforcement operator（FEO）.A solution is defined as an infeasible solution when the calculation of objective function is interrupted，or the calculated results do not agree obviously with the general knowledge.In the population initialization phase and early search phase by crossover operator and mutation operator，the generated solution may be infeasible with high probability.A feasibility enforcement operator is designed to make an infeasible solution feasible as possible.The feasibility enforcement operator means the prescriptive variation interval of some variables（such as flow stress，grain size and etc.）according to experience and the experimental data.

5 Parameter identification for magnesium alloy AZ31D

A software for parameter identification is developed by combination of the global optimization algorithm and the rigid-plastic FEM program.The parameter identification of VPDR for AZ31D magnesium alloy is carried out by using the software.

In order to provide input experimental data for parameter identification as initial value of the iteration process，a set of compression of cylindrical specimen of magnesium alloy AZ31D is carried out under different temperature，different strain rate and different strain.The distribution and its variation of grain size in the compressed specimen with deformation condition are observed experimentally.The conferences［7，10］give the detailed experimental results.The main experimental data used for parameter identification include the stress-strain curves obtained for the compression tests，grain size evolution under different deformation conditions，the load-displacement curves of the compression tests.In the parameter identification calculation，the stress-strain data used to estimate the parameter iteration initial value and selected parameter range，the load data and grain data are used to objective function calculation for evaluate the difference between the selected parameters and ideal parameters.The important input data for parameter identification of AZ31D is listed in Table 1，where Li and Ui are the lower limit and upper limit of the parameter range respectively.The identified parameters for AZ31D are listed in Table 2.In order to validate the identified results，a back extrusion process of an AZ31D part is carried out.The Fig.1 gives the formed part and the photos of the part profile where grain distribution can be measured.The back extrusion process of an AZ31D part is simulated numerically by using the obtained material parameters.A comparison of the calculated results and the experimental results on dynamic recrystallization and grain size evolution are shown in Fig.1-2 and in Table 3.It is can be seen that the calculated results agree very well with the experimental observation.

Table 1 Input dta for prameter ientification of AZ31D表1 AZ31D参数识别的输入数据

Table 2 Identified parameters for AZ31D表2 通过参数识别得出的AZ31D参数

Fig.1 Experimental results on microstructure distribution of formed AZ31D part图1 成形零件微观组织分布的实验结果

Fig.2 Simulated results on microstructure distribution of formed AZ31D part（step 124）图2 成形零件微观组织分布的数值模拟结果

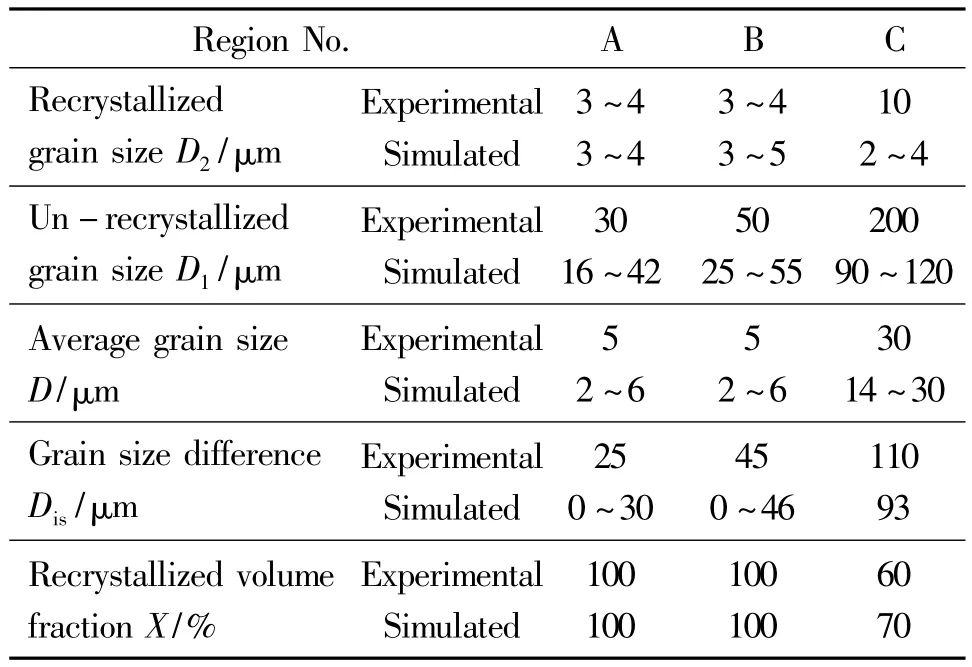
Table 3 Comparison of simulated and experimental results on microstructure for AZ31D表3 AZ31D微观组织的模拟结果与实验结果的对比

6 Conclusion

In order to identify the material parameters of VPDR，an objective function with multiple objects is established，and a HEM including RG，L-M and NL2SNO，is constructed.A special program for parameter identification is developed by a combining FEM and HEM.

By using the program，the parameter identification for AZ31D magnesium alloy is carried out.A comparison between calculated results and experimental results on the back extrusion process of an AZ31D part shows that the parameter identification program and the identified material parameters are all reliable.

Refrences:

［1］JIN Quan-lin.A New Analytical Model of Dynamic Recrystallization［J］.J Plasticity Engineering，1994，1（1）:3-13.（in Chinese）

［2］QU Jie，JIN Quan-lin，XU Bing-ye.Improvement of Visco-plastic Model Considering Dynamic Recrystallization，Acta Mechanica，2004，20（5）:499—506.

［3］MORÉ J J.The Levenberg-Marquardt Algorithm:Implication and Theory.WASTON G A，Eds.Lecture Notes in Mathematics 630:Numerical Analysis.Spring-verlag，Berlin，1978:105—116.

［4］Dennis J E，Gay D M，Welsch R E.An Adaptive Nonlinear Least-squares Algorithm［J］.ACM Trans Math Software，1981，7（3）:348—368.

［5］DUAN Q Y，SOROOSHIAN S，GUPTA V K.Effective and Efficient Global Optimization for Conceptual Rainfall-runoff Models［J］.Water Resour Res，1992，28（4）:1015—1031.

［6］Herrera F，Lozano M，Verdegay J L.1998.Tackling Real-coded Genetic Algorithms:Operators and Tools for Behavioral Analysis［J］.Artificial Intelligence Review，1998，12（4）:265—319.

［7］ZHANG Yan-shu.An Experimental Study on Thermal Deformation Behaviors and Parameter Identification for Magnesium Alloy AZ31D［D］.China Academy Machinery Science ＆ Technology，2006.

［8］HIMMELBLAU D M.Applied Nonlinear Programming［M］.New York:McGraw-Hill，1972.

［9］DUAN Q Y，GUPTA V K，SOROOSHIAN S.Shuffled Complex Evolution Approach for Effective and Efficient Global Minimization［J］.J Optim Theory Appl，1993，76（3）:501—521.

［10］ZHANG Yan-shu，ZENG Zhi-peng，JIN Quan-lin.Microstructure Properties Study of Commercial Magnesium Alloy AZ31D［J］.Materials Science Forum，2004，488-489:641.

［11］QU Jie.Parameter Identification Challenges in Macromicro Coupled Constitutive Model.LIU Ying-hua，LIU Kai-xin，NING Jian-guo，Eds.Advances in Plastic Mechanics-2011 China Plastic Mechanics Conference Proceeding［M］.Beijing:Tsinghua University Press，2011:150—155.（in Chinese）

［12］QU Jie，JIN Quan-lin，XU Bing-ye.Parameter Identification for Improved Viscoplastic Model Considering Dynamic Recrystallization［J］.International Journal of Plasticity，2005，21（7）:1267—1302.