具有给定测地线的三次三角Bézier曲面的构造与拼接

郭清伟， 张官升

（合肥工业大学 数学学院，安徽 合肥 230009）

在日常生活中会遇到许多需要构造曲面的问题，特别是在服装设计、鞋制造业等行业，通常要求设计者在给定的曲线上设计出需要的曲面，而给定的曲线是不允许改变的，但可以通过修改其他地方来满足人们的审美要求。将给定的曲线作为所要构造的曲面的测地线越来越受到设计者的青睐，而测地线就是曲面上测地曲率处处为0的曲线。

以给定的曲线为边界测地线构造曲面一直受到国内外研究者的关注。文献［1］利用Frenet标架研究了以给定曲线为边界测地线的曲面构造问题，所构造的曲面为直纹面，给出了所构造曲面以给定曲线为边界测地线的充要条件；文献［2］对给定的三次Bézier曲线，利用所构造曲面的切平面与所给曲线的法平面之间所应满足的关系，研究了以给定的三次Bézier曲线为边界测地线的曲面构造问题，避免了利用Frenet标架和曲线的弧长参数化，所构造的曲面也是直纹面；文献［3］把以给定多项式曲线为边界测地线的曲面构造问题转化为插值问题；基于Hermite插值方法，文献［4］研究了以给定的2条空间曲线为边界测地线的曲面构造问题；文献［5－6］讨论了给定空间4条多项式或有理Bézier曲线构成的曲边四边形，构造张量积Bézier曲面，使所构造的曲面以给定的曲线为边界测地线的问题；文献［7］讨论了以给定的空间曲线为边界测地线构造三角Coons曲面片的问题；文献［8］讨论了以给定的空间三次多项式Bézier曲线为边界测地线的可展曲面的构造及G1连续性问题。

本文利用一条曲线为所在曲面的测地线当且仅当其从切面与该曲面在这条曲线上的切平面重合这一论断，对给定的三次Bézier曲线构造三次三角Bézier曲面，使该曲面以给定的曲线为其边界测地线，给出了用给定曲线的控制顶点表示所构造曲面的控制顶点的表达式；讨论了具有公共测地线的2个三次三角Bézier曲面的C1和G1连续性；为了说明所给方法的有效性，给出了几个数值实例。

1 背景知识

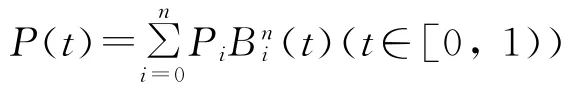
定义2 设Pij∈R3（i＝0，1，…，m；j＝0，1，…，n），称参数曲面

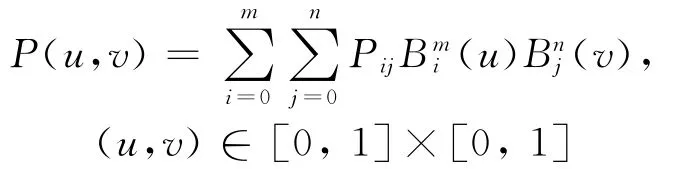
为m×n次张量积Bézier曲面。其中，（u）和（u）为m和n次Bernstein基函数。

定义3 设Pi，j，k∈R3（i，j，k≥0，i＋j＋k＝n），称曲面

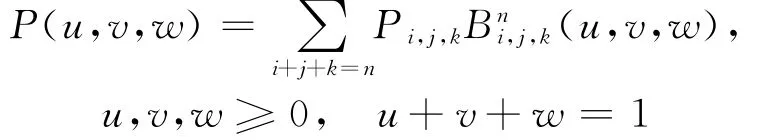
为n次三角Bézier曲面，其中

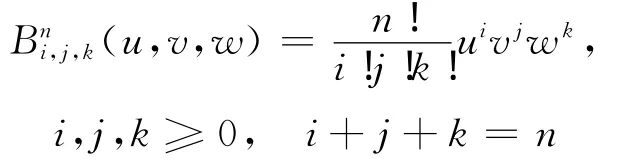
称为二元n次Bernstein多项式。

曲面上的测地线是曲面上一类重要的曲线，被称为“曲面直线”。关于测地线有如下引理。

引理1 设曲面S：r＝r（u，v）上一曲线C：u＝u（t），v＝v（t）（t为参数），其主法向量为N，曲面S在C上的法向量为n，则曲线C为测地线的充要条件为：N∥n［9］。

2 给定测地边界线的三角Bézier曲面构造

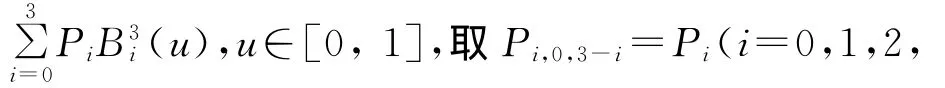
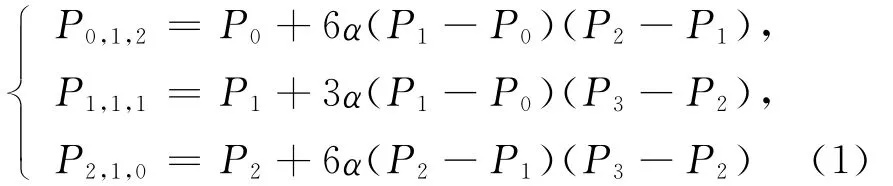
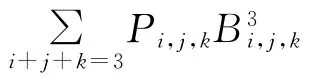
证明 由定理条件显然有P（u，0，w）＝P（u），u∈［0，1］，w＋u＝1。下证P（u，0，w）为曲面P（u，v，w）的边界测地线。因为

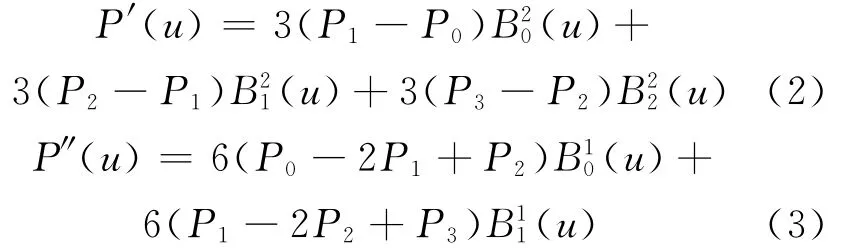
所以由（2）式、（3）式可得：

由Pi，0，3－i＝Pi（i＝0，1，2，3）和（1）式可得曲面P（u，v，w）在边界P（u，0，w）上关于u和v的偏导数分别为：

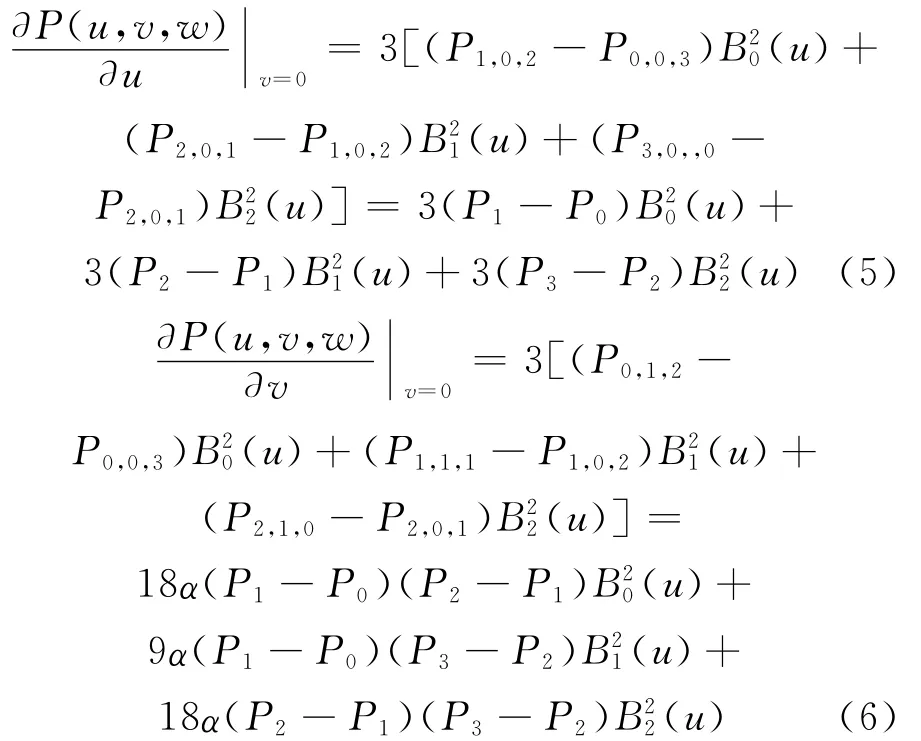
对（6）式关于μ进行一次升阶得：

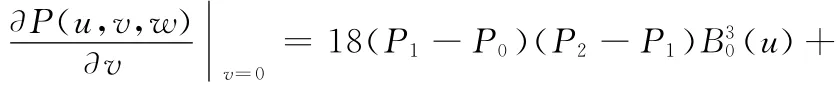
由（2）式、（4）式、（5）式、（7）式得曲线P（u）＝P（u，0，w）的主法向量与三次三角 Bézier曲面P（u，v，w）在边界P（u，0，w）上的法向量满足：

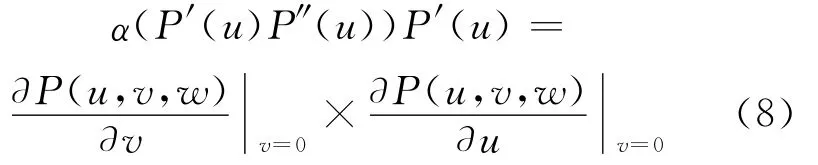
由引理1可知P（u，0，w）为曲面P（u，v，w）的边界测地线。

由定理1可得如下推论。

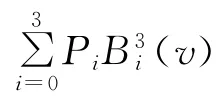
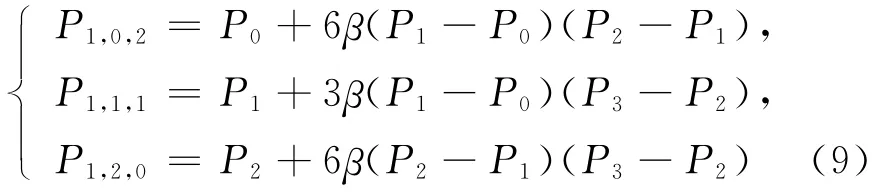
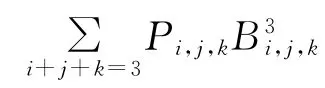
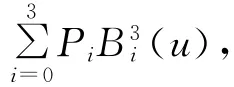
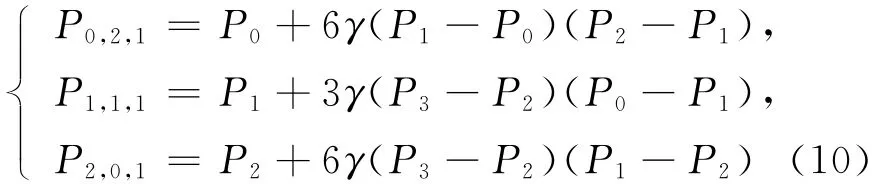
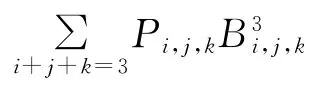
3 2个三次三角Bézier曲面的连续性

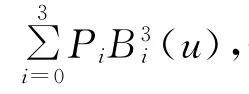
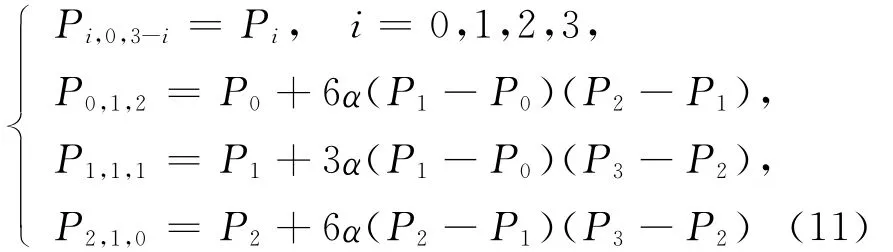
和

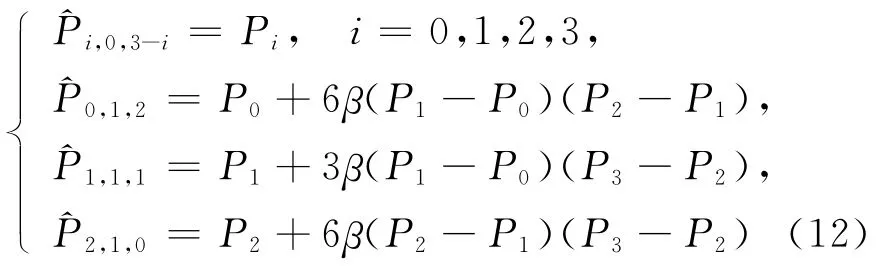
构 造 三 次 三 角 Bézierr曲 面P（u，v，w）＝（u，v，w），u，v，w≥0，u＋v＋w＝1和（u，v，w）＝（u，v，w），u，v，w≥0，u＋v＋w＝1，则有：① 曲线P（u）为三次三角Bézier曲面P（u，v，w）和（u，v，w）的公共边界测地线；② 当β＝－α时，P（u，v，w）和（u，v，w）是C1连续的；③ 当β≠－α，但αβ＜0时，P（u，v，w）和（u，v，w）是G1连续的。这里α、β为非零常数。

（11）式中的α与（12）式中的β异号是为了确保P（u，v，w）和（u，v，w）在公共边的两侧。

证明 （1）由定理1可得曲线P（u）＝P（u，0，w）＝（u，0，w），且为三次三角 Bézier曲面P（u，v，w）和（u，v，w）的边界测地线。

（2）由定理条件可得：

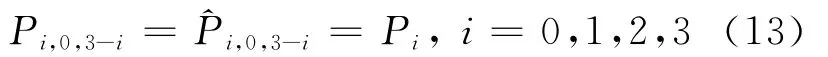
当α＝－β时有：

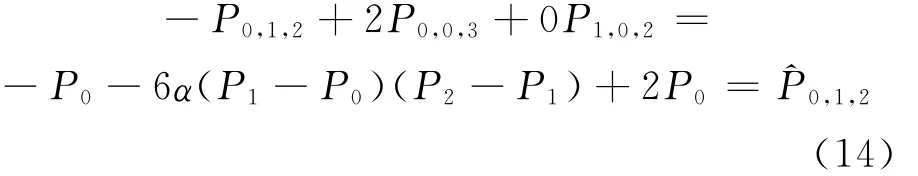
同理可得：

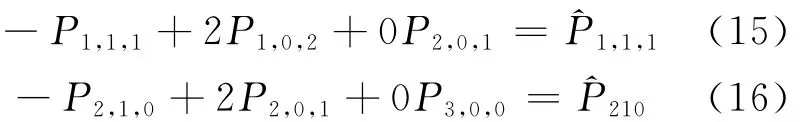
根据文献［10］，由（13）～（15）式知三次三角Bézier曲面P（u，v，w）和（u，v，w）在公共边界是C1连续的。

（3）当β≠－α，但αβ＜0时，由定理条件可得：

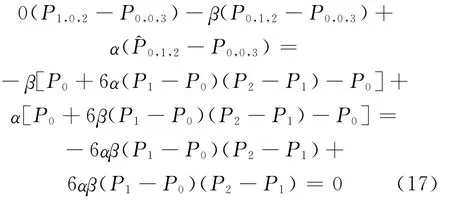
同理可得：

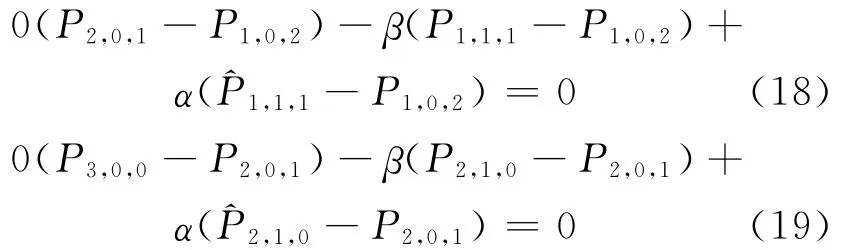
根据文献［10］，由（13）式和（17）～（19）式知三次三角Bézier曲面P（u，v，w）和（u，v，w）在公共边界是G1连续的。

4 数值实例

图1所示为按定理1当α取不同值，而P0，3，0、P0，2，1、P1，2，0取相同值时所构造的具有公共测地线的2个三次三角Bézier曲面；图2所示为按定理2当α、β取不同值，P0，3，0、P0，2，1、P1，2，0取不同值时所构造的具有公共测地线的2个三次三角Bézier曲面。

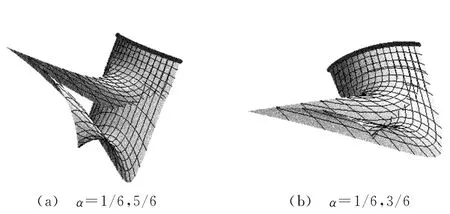
图1 按定理1当α取不同值时所构造的具有公共测地线的2个三次三角Bézier曲面

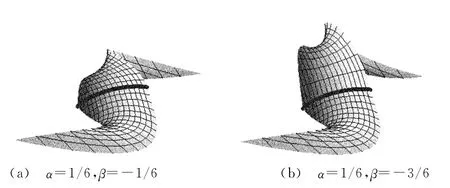
图2 按定理2当α、β取不同值时所构造的具有公共测地线的2个三次三角Bézier曲面

5 结束语

本文利用一条曲线为所在曲面的测地线的充要条件是其从切面与该曲面在这条曲线上的切平面重合，给出以给定的三次Bézier曲面为边界测地线的三次三角Bézier曲面的构造方法，得到了用所给曲线控制顶点表示所构造曲面的控制顶点的表达式，讨论了具有给定公共测地线的组合三次三角Bézier曲面的连续性。将进一步研究对给定的n次（n≥4）Bézier曲线，如何构造以给定曲线为边界测地线的n次三角Bézier曲面，以及如何构造2条边界或3条边界均为所构造的三角Bézier曲面的边界测地线的曲面构造问题。

［1］ Wang Guojin，Tang Kai，Tai C L.Parametric representation of a surface pencil with a common spatial geodesic［J］.Computer－Aided Design，2004，36（5）：447－459.

［2］ Marco Paluszny.Cubic polynomial patches through geodesics［J］.Computer－Aided Design，2008，40（1）：56－61.

［3］ Sánchez－Reyes J S，Dorado R.Constrained design of polynomial surfaces from geodesic curves［J］.Computer－Aided Design，2008，40（1）：49－55.

［4］ Sprynski N，Szafran N，Lacolle B，et al.Surface reconstruction via geodesic interpolation［J］.Computer－Aided Design，2008，40（3）：480－492.

［5］ Farouki R T，Szafran N，Biard L.Construction of Bézier surface patches with Bézier curves as geodesic boundaries［J］.Computer－Aided Design，2009，41（11）：772－781.

［6］ Farouki R T，Szafran N，Biard L.Existence conditions for Coons pathes interpolating geodesic boundary curves［J］.Computer Aided Geometric Design，2009，26（5）：599－614.

［7］ Farouki R T，Szafran N，Biard L.Construction and smoothing of triangular Coons patches with geodesic boundary curves［J］.Computer Aided Geometric Design，2010，27（4）：301－312.

［8］ Li Caiyun，Wang Renhong，Zhu Chungang.Design andG1connection of developable surfaces through Bézier geodesics［J］.Applied Mathematics and Computation，2011，218（7）：3199－3208.

［9］ 宋卫东.微分几何［M］.北京：科学出版社，2009：82－89.

［10］ 周蕴时，苏志勋，程少春.CAGD中的曲线与曲面［M］.长春：吉林大学出版社，1993：209－217.