客车车内噪声声固耦合分析与优化

2014-12-31张代胜庄隽涛

合肥工业大学学报（自然科学版） 2014年1期

张代胜，庄隽涛

（合肥工业大学机械与汽车工程学院，安徽合肥 230009）

目前客车车内降噪往往通过实验来解决，此时车身结构已经定型，对于结构产生的低频噪声难以合理解决。随着计算机技术和有限元理论的发展，在产品设计阶段就利用数值方法对车内噪声进行预测并提出修改，对于提升整车声品质和整车开发改进都有重要意义。本文建立了大客车车内声腔与结构耦合的有限元模型，利用谐响应分析方法得到了车内测点的声压曲线，针对峰值频率基于灵敏度的优化分析方法，对车身结构提出改进措施，以降低车内噪声峰值，为车内声学设计奠定基础。

1 耦合系统有限元理论

车身结构为弹性体，当车身板件发生振动时，会引起车内声压分布的变化，同样，当车内声压发现变化时也会激起车身板件的振动，这就形成彼此相互作用的声固耦合系统。客车内部结构构成了一个封闭系统，将其离散化可得空腔的声学有限元模型，忽略声学阻尼作用，其有限元方程为：

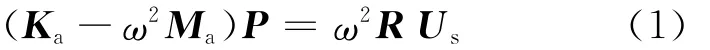
其中，Ma为声学质量矩阵；Ka为声学刚度矩阵；P为声压向量；R为流固耦合矩阵；Us为节点位移幅值向量。

对于结构，需要考虑声压对结构的作用，其有限元方程为：

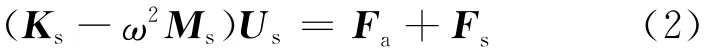
其中，Ms为结构质量矩阵；Ks为结构刚度矩阵；Fs为施加于车身上的外力；Fa＝RTP。

将（1）式和（2）式联立可得耦合系统稳态频域方程［1－2］：

简化写为［3］：

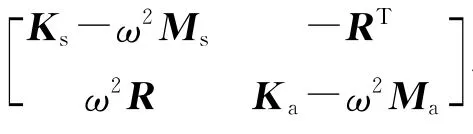
（3）式两端乘ejωt，设u＝Uejωt，f＝Fejωt，则（3）式的时域形式为：

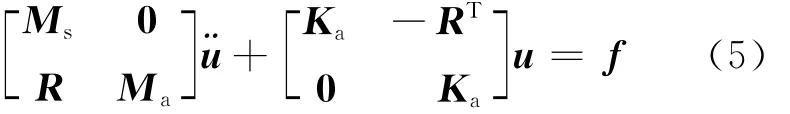
2 耦合模型频率响应分析

2.1 客车声固耦合模型的建立

在不影响结构的前提下，对车身骨架进行简化，去除非承力件和一些细微特征，利用 Hypermesh对结构进行建模。为构成封闭的空腔，在车身骨架的基础上画出内饰蒙皮、玻璃和车内地板。在结构模型基础上，抽出与乘员舱声学空腔模型相关的零件、玻璃等，用于建立乘员舱声学空腔模型的外表面。为保证每个波长内有6个声学单元，声腔网格大小取为100mm，用四面体单元对之前处理好的声腔包络面网格进行实体网格划分。由于座椅对声腔的分隔作用往往对声压分布有较大影响，在此引入座椅单元，座椅模型的材料密度为空气模型的10倍。全模型共有壳单元476 645个，实体单元155 162个。

在建立好结构模型和声腔模型后，为了使声腔单元的节点随结构一起运动，需要调整声腔节点的位置，使其与对应的结构节点重合，并在控制卡片中加入ACMODL卡片使模型中重合的节点耦合在一起［4］。有限元模型如图1所示。

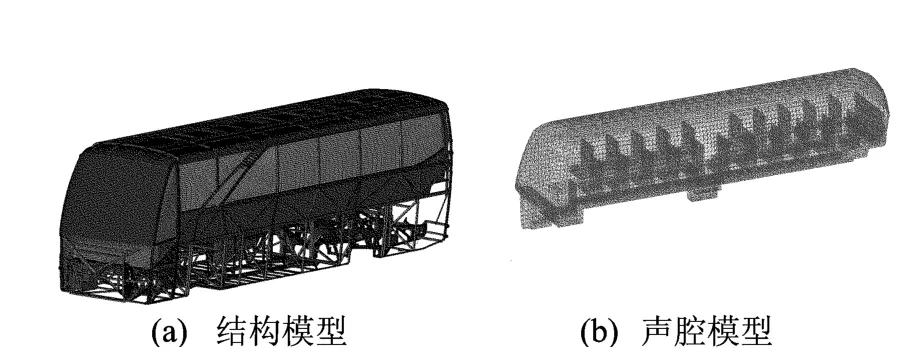
图1 有限元模型

2.2 车身声学灵敏度计算

车身声学灵敏度指单位激励力作用在车身支撑点，在人耳处测得的噪声级，常用P／F表示，其单位是dB，参考值为20μPa／N。在发动机左后悬置点施加幅值为1N的正弦激励，结构声是低频噪声的主要来源，由于客车结构的特殊性，有可能发生声振耦合影响声品质的耦合频率均在100Hz以内，故将扫频频率定为0～100Hz，步长为2Hz，全车无约束条件，根据实车后排乘员受噪声影响最严重的特点，输出最后排乘员右耳测点的x向位移，由于耦合矩阵的引入使（5）式呈非对称性，给求解带来不便，用NASTRAN的声学求解模块SOL111求解计算。发动机悬置激励下车身声学灵敏度曲线如图2所示。

图2 发动机左后悬置激励下车身声学灵敏度曲线

由图2可知在40、72、86Hz处有比较明显的峰值，最大峰值在72Hz处为71.24dB。左后悬置动刚度分析曲线如图3所示。由图3可发现在垂向方向72Hz时出现峰值，反映该点在受到72Hz的垂向激励时，容易通过传递路径传入乘员耳部，说明传递路径隔振效果不佳，人耳对激励依然敏感。

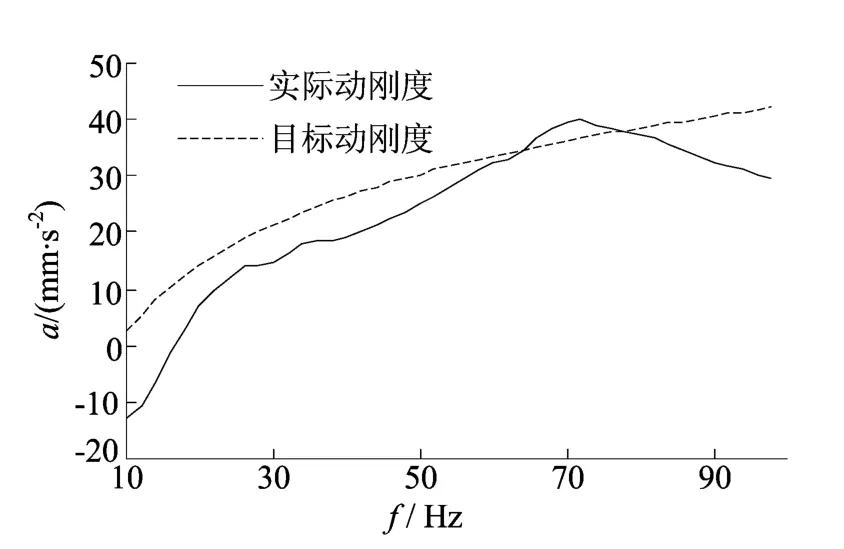
图3 左后悬置点动刚度分析曲线

2.3 车内噪声响应的实验分析

实验工况为4挡、5挡下不同车速匀速行驶，测点为发动机左后悬置车架端（1#）、最后排座椅处（4#）、右前减震器安装点（10#），图4所示为2种工况下各测点加速度响应，由图4可知4挡60km／h（激励频率70.5Hz）和5挡90km／h（激励频率为73.0Hz）为振动峰值工况，正好对应动刚度分析中传递路径需要改善的频率附近。

道路实验时重点关注了90km／h（1 408r／min）匀速行驶工况，利用声级计测量车内噪声并记录其时间历程信号，测点布置在最后排偏左位置乘员的右耳位置，测点的“A”计权声级曲线如图5所示。从图5可知，当车辆以5挡90km／h匀速行驶时，在70～80Hz频率段有明显的噪声峰值，这验证了之前的仿真结果，可知左后悬置在该频率下的垂向激励容易引起后排乘客测点声压的升高；低频范围的其他峰值可能是由于在其他激励点某方向作用下，激励点到响应点传递路径不理想造成的。

图4 各测点加速度响应曲线

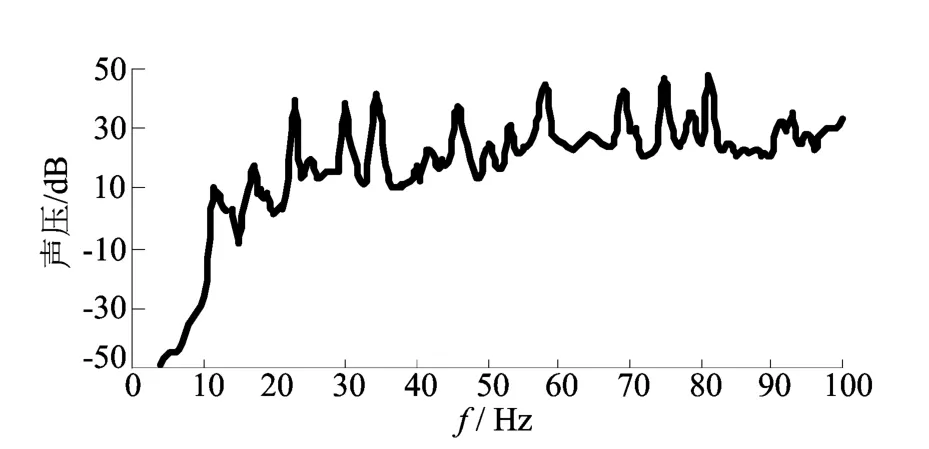
图5 90km／h匀速行驶时声压响应

3 车内噪声优化分析

3.1 杆件灵敏度分析

杆件灵敏度就是指测点灵敏度Lp对设计变量xi变化的敏感程度［4］，表示为：

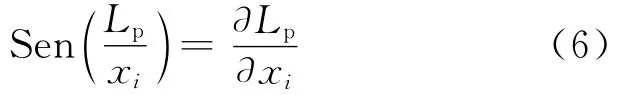
由于该客车已经上市销售，不方便对结构进行大的修改，考虑到实际操作可能性，选择骨架厚度作为设计变量［5］，通过灵敏度分析方法，找出各峰值频率下对测点声压影响大的杆件，且对质量灵敏度低的杆件，即将相对灵敏度大的杆件作为下一步优化的设计变量。以测点声压为目标函数，分别计算40、72、86Hz下杆件厚度对声压的灵敏度Kp；再以质量最轻为目标函数，计算各杆件厚度对整车质量的灵敏度Km，相对灵敏度的计算公式为Kref＝Kp／Km［6］。最后分别取3个频率下排名前25的杆件，并消除重复项得到66个最终的优化变量。表1所列为72Hz时部分杆件的灵敏度值。

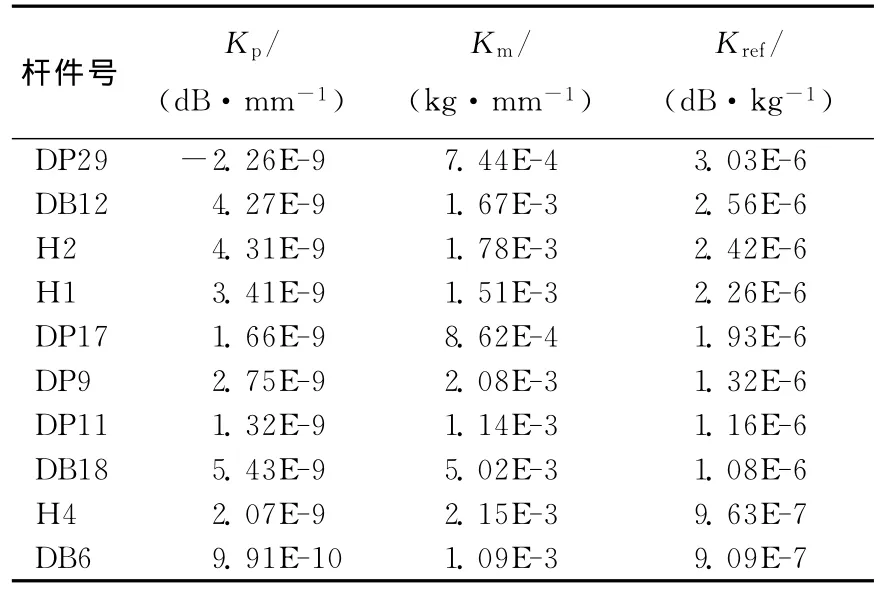
表1 72Hz下部分杆件灵敏度

3.2 优化设计

指定点声压优化设计问题可表示为：

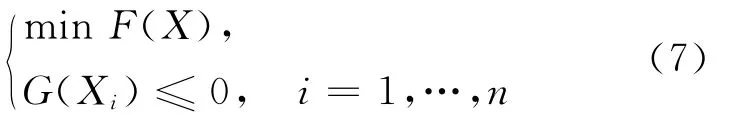
其中，F（X）为目标函数；G（Xi）是由设计变量和状态变量的约束条件所构成的约束函数。

3.2.1 目标函数

根据2.2中仿真结果，在40、72、86Hz出现了噪声峰值，选取各频率的加权系数乘以该频率的声压响应幅值作为目标函数，目标函数可表示为［7］：

其中，ci为第i个频率的加权系数，见表2所列；Lpi表示第i个频率的声压响应峰值。

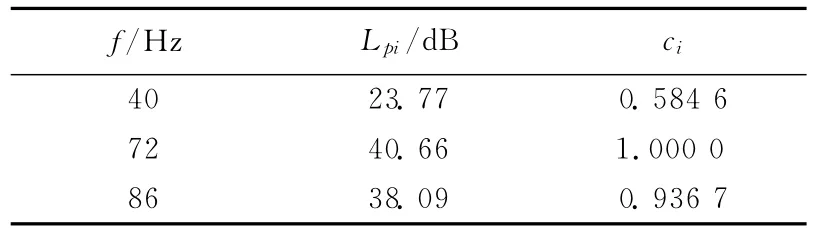
表2 各相关频率加权系数

3.2.2 约束函数

为保证优化后结构不至于出现整车重量激增或局部强度达不到设计要求，控制整车质量的变化在50kg以内，即3.794≤G1（x）≤3.894。

同时，保证优化后结构的弯曲刚度和扭转刚度不低于原模型，弯曲刚度以车架中部变形最大节点位移来代表，扭转刚度以左前悬架弹簧支点位移来代表［8］，表示为：G2（x）≤3.458×10－5，G3（x）≤1.795×10－4。

设计变量选取灵敏度分析中得到的66根相对灵敏度较高的杆件，采用Optistruct优化模块进行求解计算，迭代7步后结构收敛。优化后的杆件厚度带多位小数，需调整后才可用于实际生产。改进后模型质量为3.901t，比原模型增加57kg。对改进后结构重新进行车内噪声仿真计算，优化前后后排测点声压曲线如图6所示。

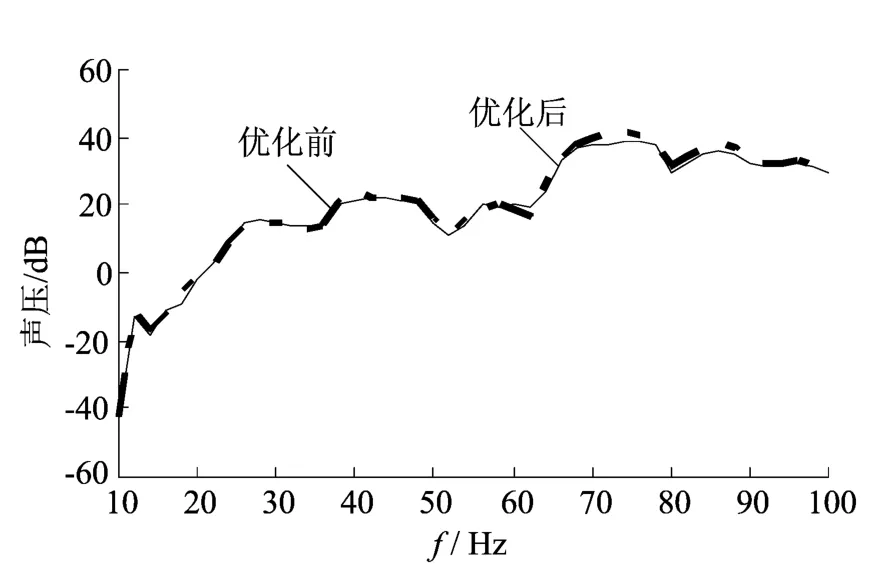
图6 优化前后后排乘员测点声压曲线对比

3.3 板块贡献量分析及优化

将车身内饰壁板、地板、顶棚、风窗、驾驶台分为28个板块，通过激励发动机左后悬置，以最后排乘员耳旁声压为响应，计算可得各板块对耳旁声压的贡献大小，贡献量占前8的板件排序为：地板（后）、后围板、地板（中）、顶盖（后）、后围玻璃、地板（前）、右玻璃（后）和左玻璃（后）。

针对这些板件，可选取合适的制振方法，对于地板、顶盖、侧围可采取喷涂减振阻尼胶的方法抑制对响应点有正贡献量的板件振动，对于玻璃振动可通过更改单块玻璃厚度来实现，避免无谓地增加整车质量。对更改过后的结构重新计算声压响应并和制振前相对比，结果如图7所示，由图7可见，整车整体噪声比杆件结构优化后的结果有了一定的降低，验证了板块贡献分析的结果。