偏最小二乘回归法对玉米水肥耦合单因子效应分析

2014-12-31贺冬梅

中国农业信息 2014年23期

文/贺冬梅

山西省朔州职业技术学院山西朔州 036002

偏最小二乘回归是一种新型的多元统计数据分析方法，集多元线性回归分析、典型相关分析和主成分分析的基本功能于一体，将建模预测类型的数据分析方法与非模式的数据认识性分析方法有机的结合在一起，研究的焦点是多因变量对多自变量的回归建模[1、2]。

水分和养分是作物生长的主要限制因子。不同的土壤水分条件下对肥料的利用率存在明显差异，不同施肥条件下对作物的生长发育同样具有重要影响，水分缺乏限制了作物生产力的提高，养分不足制约着作物对水分的高效利用[3]，因此因地制宜的调节水分和养分，使它们处于合适的范围，达到“以水促肥，以肥调水”的目的，对节约水、肥资源和保护环境将有重要的意义[4、5]。

1 试验设计

本大田研究试验地点安排在贵州省毕节市梨树镇平乡村，供试土壤为黄色壤土，有机质含量为19.292g/kg，全氮0.196%，全磷 0.830g/kg ，全钾 6.270g/kg，碱解氮 91.2mg/kg，速效磷48.68mg/kg，速效钾258.34mg/kg，pH值7.22，田间持水量为46.24%。供试玉米品种为毕单13号，2005年4月14日播种， 4月20日出苗， 9月9日收获，全生育期149天。

大田试验方案采用四因素三水平L9(34)正交设计，总处理数为9个（见表1），各处理重复3次，设置27个小区，小区面积为6m2，种植32株玉米。

2 结果与分析

2.1 回归模型建立

以籽粒产量(表1)作为目标函数（因变量），以田间持水量（W）、施氮量（N）、施磷量（P）、施钾量（K）作为自变量，经DPS统计软件分析，采用偏最小二乘回归进行模拟，求得籽粒产量与自变量的数学回归模型：

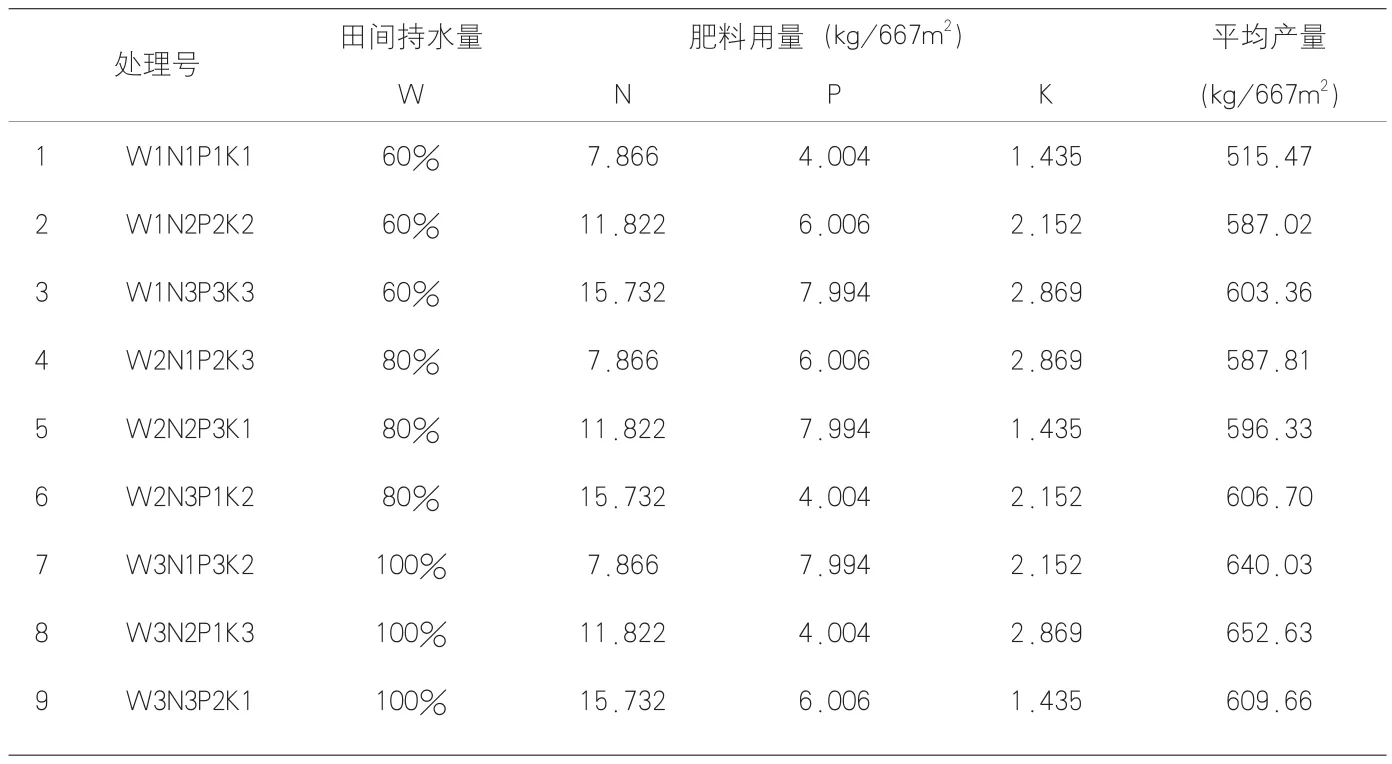
表1 试验方案

经分析，回归模型数据标准化后误差平方和＝0.69889，决定系数R2＝0.91264，模型残差＝5.80431，说明模型与实际情况拟合较好。

2.2 因子效应分析

2.2.1 单因子效应分析

图1 产量单因素效应分析

对模型（1）采用“降维法”可解析出其他因子居一定水平时的效应，相当于作多组单因子试验。将其中一个因子做变量，其他三个因子固定为零水平，得到各因子与籽粒产量的一元二次回归子模型为：

将因子的水平分别除以各自的最大值，以得到归一化的X轴坐标，由以上方程(2,3,4,5)做图，可得到单因素对籽粒产量的变化规律(图1)。在各因素水平范围内，单因素对籽粒产量的变化表现为近似一次函数。由图1可得，在各因子试验设计水平范围内，各因子对产量都具有增产效应，其中，施入过多的N，K会造成产量的下降。

2.2.2 单因子灵敏度分析

灵敏度＝边际函数/平均投入产出效应

模型参数的灵敏度分析，是对数学模型的参数动态变化过程，即瞬时变化过程进行分析。

图2 单因子灵敏度分析图

图3 单因子边际效应分析图

将其中一个因子做变量，其他三个因子固定为零水平,采用唐启义等的DPS统计软件计算，得到W、N、P、K各因子的系数灵敏度，依据这些数据，做因子系数灵敏度分析图。

由图2可知，单因子灵敏度呈曲线变化

趋势，随因子水平的增加，灵敏度呈下降趋势。在试验设计范围内，各系数灵敏度均大于1，说明单因子的边际产量大于平均效应产量，且平均效应产量是呈递增趋势的。

2.2.3 单因子边际效应分析

边际产量可反映各因素的最适投入量和单位水平投入量变化对产量增减速率的影响。

对方程（2，3，4，5）求一阶倒数可得各因子在不同水平条件下的边际产量，同时做各因子的边际产量效应图。

由图3可知，各因子的边际产量均为正值，说明产量呈递增趋势，各因子对产量都有增产效应，水分和磷的边际产量是呈递增趋势的，随因子水平的提高，水分和磷对产量的增长较迅速，说明增加土壤水分和施磷量的增产效益较高；氮和钾在试验范围内，边际产量是呈递减趋势的，说明增加施氮量和施钾量对产量的增产效益较低。图3函数的斜率代表对边际产量影响的大小程度，正负代表对边际产量的增减，其中水分的增产效应最大，这与金剑等的研究是一致的，增加单位水平土壤水分的增产量大于增施单位水平肥料的增产量。