一种大直径薄壁输水管道敷设的计算方法
2014-12-31吴云云
孟 强,吴云云
(吉林省水利水电勘测设计研究院,吉林 长春 130021)
1 问题的提出
跨海输水管道具有管径大、管壁薄及敷设难度大等特点,以“舟山市大陆引水二期工程”为例,采用Q235b钢管,管道内径1200mm,壁厚14mm,属于大直径薄壁管道[1]。大直径薄壁输水管道理论研究国内外尚不成熟,理论分析主要依据海洋石油管道敷设理论。海洋石油管道具有管径小、管壁厚、刚度大的特点,比大直径薄壁输水管易敷设,一些计算理论并不适用于大直径输水管道。
随着沿海跨海输水工程的不断发展,管道敷设技术不断提高以及国内大型敷管船的科技创新,为大直径海洋输水管道敷设提供了有力的技术支撑。跨海输水管道多为浅海铺设,由于管线路由长、易受海洋洋流及潮汐流影响,海底定位难度大。敷管船法是国内沿海跨海输水管道敷设应用最广泛的方法,根据不同的海洋因素及管道性质,逐步发展为4种更具体的作业方法:S型铺管 (S—LAY)、J型铺管 (J—LAY)、卷盘铺管 (REEL—LAY)和拖管法(Tow—Method)[2]。
S型 (S—LAY)铺管法主要应用于水深不大于8m的海域,管道可在敷管船上完成对中焊接,并利用船尾的托管架将管道敷设至海底,管道位移呈现一个被拉长的分为3个部分的“S”型:管线端部至对中焊接处的直线段、管道脱离船尾至托管架最后一个滚轮处的上弯段以及管道脱离托管架至管道与海床接触点处的下弯段 (见图1)。管道下弯段承受较大的水头压力且只有2个支撑点,敷设时管壁不发生屈服变形是敷设成功的关键。目前工程实践中大多数根据工程经验确定下弯段敷设长度,缺乏理论依据,因此研究敷管船管道应力变化具有重要意义。
本文通过数学模型计算分析,在黄玉盈、朱达善[3]运用奇异摄动法推求的非线性方程组的基础上,运用MATLAB软件的二次开发,迭代计算得到管壁应力应变关系,并结合现场陆上模拟试验,分析管道受力状态,验证计算方法的合理性。
2 悬空段管道的控制方程及其解
奇异摄动理论是摄动论的一种计算方法,摄动理论是现代应用数学的一个分支,是解决非线性变系数方程近似解析解的有效方法。
管段微元受力情况见图2,其平衡方程为:
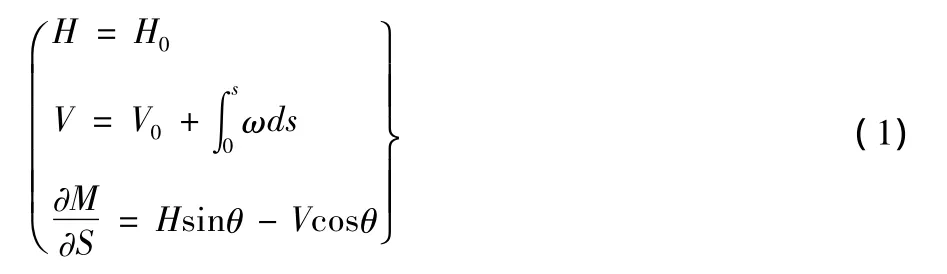
式中:S为管道弧长(原点处值为0),m;θ为管线上任一点切线与水平线的夹角,rad;H为管线横截面水平力,kN;H0为管线横截面原点处水平力,kN;V为管线横截面铅直力,kN;V0为管线横截面原点处铅直力,kN;M为管线横截面弯矩,kN·m;ω为单位长度的管重,kN。
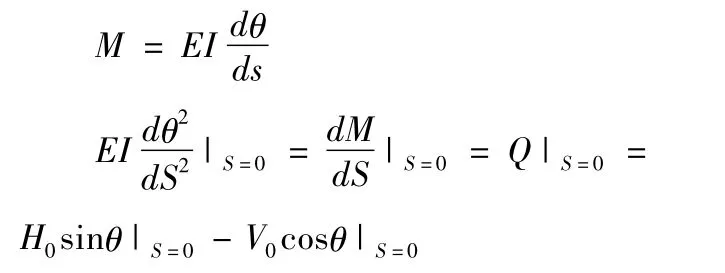
式中:EI为管道截面的弯曲刚度,kN·m2;Q为管道剪力,kN。
(1)式可变为:
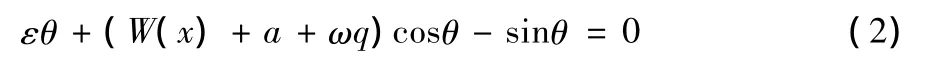
方程(2)式就是用无量纲量表示的管道控制方程,对于敷管船,由于H0和L比较大,因此,是一个小于1的小参数。
根据敷管船上托管架、张紧器及海底地基协调变性条件,黄玉盈、朱达善运用奇异摄动法推导出关于H及L的非线性方程组[3]:

3 非线性方程组迭代计算方法探讨
方程组 (3)非线性高且含有积分表达式,直接求解难度大,采用一般的迭代方法,虽编制程序简单,但方程组对所赋初值的要求比较苛刻。赋初值不当,方程组可能不收敛、计算结果无解或解与实际偏差大,计算结果较差。牛顿迭代法,收敛速度快,但求Jacobi矩阵要计算n个偏导数值,偏导数计算过程较复杂,计算量大,特别是分量函数复杂时,牛顿法计算难以实现收敛。为避免多次求偏导数,减小计算量,本文采用离散型Newton法,用差商代替偏导数,不仅简化了复杂的计算程序,而且收敛速度快,计算结果精确。
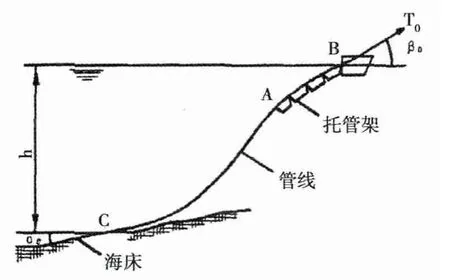
图1 管船法示意图

图2 管段微元受力分析图
3.1 离散Newton法原理
设有非线性方程组:

式中:e为单位向量,且ek(k=1,2,……,n)的离散第k个分量为1,其余分量为0,迭代公式为:
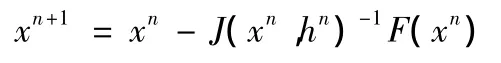
式中:h=(h1,h2,………,hn)T,即迭代步长。
3.2 迭代步骤:
(1)赋初值x0(包含H,L的一个数组),h(迭代的步长);
(3)计算f(x(k))、f(x(k)+h(k)ei)(i=1,2)以及矩阵:

(4)再计算新的x值,即x(k+1)=x(k)-J(x,h)f(x(k));
(6)迭代结束,输出结果。
4 MATLAB编程求解结果与现场试验比对分析
为验证计算结果的准确性,以“舟山市大陆引水二期工程”跨海输水管道为例,运用MATLAB软件编程求解,分别就管道悬空高度为2,6m两种情况,选取管道位移曲线及管壁应力值,其结果与上海基础公司陆上试验数据[4]作比较。试验数据中有部分点偏离曲线较大,主要原因是工程现场数据量大,存在个别试验数据采集不准确的现象。剔除不准确点,对比结果显示,计算结果与试验结果吻合较好 (见图3~6)。

图3 悬空2m位移比对图
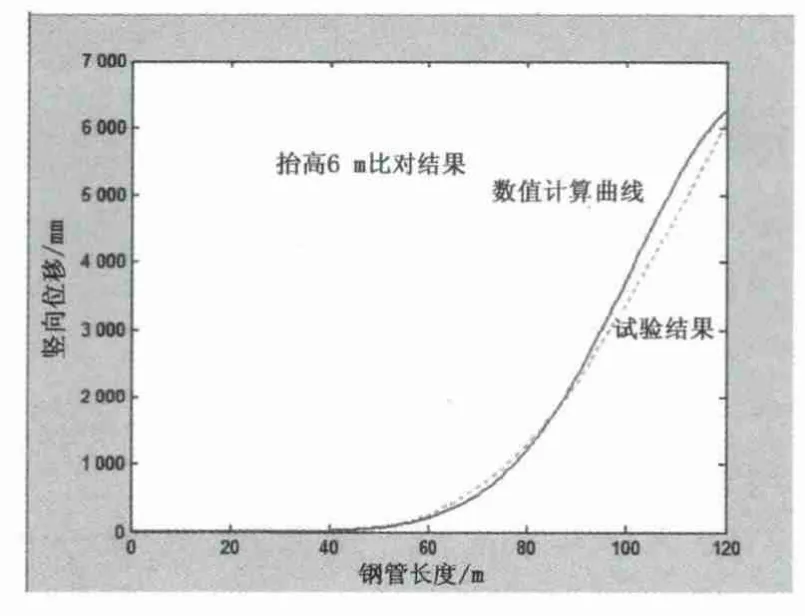
图4 悬空6m位移比对图

图5 悬空2m应力比对图
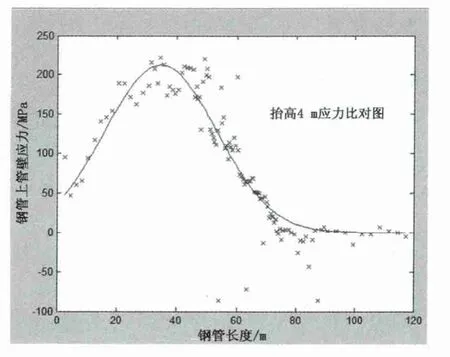
图6 悬空6m应力比对图
5 结语
通过以上分析可以得到以下结论:
(1)运用离散型Newton法,用差商代替偏导数求导的计算方法,简化了计算过程,降低了计算难度,收敛性较好;
(2)通过计算结果与现场陆上试验结果比对分析,数值迭代计算结果与试验数据吻合度较好,验证了计算方法的合理性;
(3)计算结果可供施工设计参考,对工程实际具有重要理论参考价值。
[1]郭浩亮,陈雯,何伟,等.舟山大陆引水二期初步设计报告[R].杭州:浙江省水利水电勘测设计院,2008.
[2]王庆国,吕伟,张向峰,等.先进深水S型托管架概念设计研究[C] //中国海洋工程学会.第十四届中国海洋 (岸)工程学术讨论会论文集.大连:大连理工大学,2009:141-146.
[3]黄玉盈,朱达善.海洋管道铺设时的静力分析 [J].海洋工程.1986,4(1):32-46.
[4]上海基础公司试验室.舟山大陆引水二期管道现场实验报告[R].上海:上海基础公司,2009.
