InSAR卫星编队构形多约束优化设计方法研究
2014-12-31刘培玲童庆为
刘培玲,黄 欣,陈 祥,童庆为,宋 涛
(上海卫星工程研究所,上海 200240)
0 引言
随着德国TanDEM_X卫星任务的成功在轨运行,InSAR卫星的技术优势备受关注。作为In-SAR卫星在轨成像的重要技术支撑,InSAR卫星编队飞行构形的设计问题显得尤为重要。对卫星编队构形设计进行了大量研究,分析了串行编队、星下点圆形、空间圆形、干涉车轮和干涉钟摆等典型编队构形对SAR卫星成像性能的影响[1-4]。其中,文献[4]以时间比作为优化指标,基于遗传算法进行了构形的优化设计,认为双星空间编队是进行InSAR测高的理想构形。在工程实践中,In-SAR卫星编队不仅需要测绘基线长度满足要求,而且对InSAR卫星受摄动时的编队构形安全性提出了要求,而目前常见的编队构形设计方法对这些要求考虑不全[5-7]。为此,本文针对InSAR卫星编队构形的设计要求,以e/i矢量表示的编队运动学方程为基础,考虑InSAR卫星测绘过程中的约束和构形长期安全性约束,对InSAR卫星编队构形优化设计进行了研究[8-10]。
1 基于e/i矢量的编队运动学方程
定义轨道坐标系o-xyz:原点o在轨道上与卫星质心重合;ox轴沿矢径方向,背向地心;oz轴与轨道平面垂直,指向轨道面法线方向;oy轴按右手法则指向飞行方向。相对运动坐标系与地心惯性坐标系如图1所示。
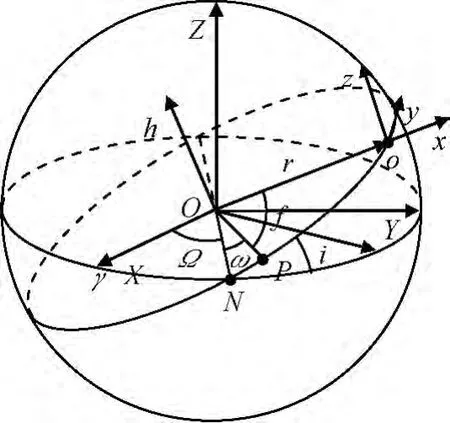
图1 相对运动坐标系与地心惯性坐标系Fig.1 Orbital coordinate system and geocentric inertial coordinate system
设r,u,i,Ω分别为卫星星的地心距、纬度幅角、轨道倾角和升交点赤经。对参考性和伴随星有
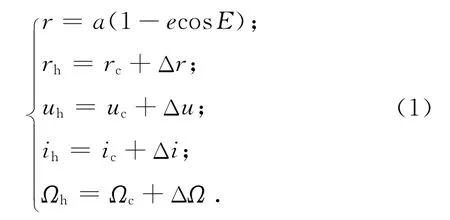
式中:a为半长轴;e为偏心率;E为偏近点角;下标c,h分别表示参考星和伴随星;Δ表示两星相应变量的差值。由文献[1、8]可知:当参考星与伴随星的相对距离较近时,能近似认为相对运动参数为小量,可将编队卫星的相对运动学方程简化为
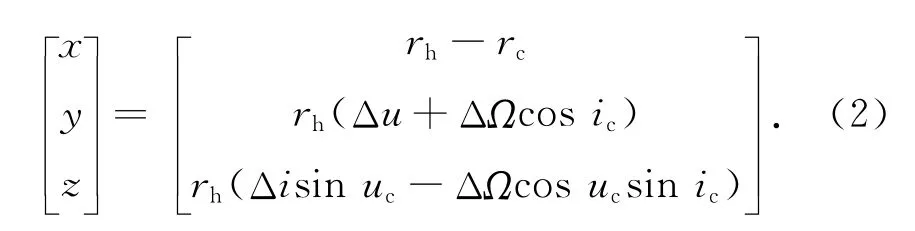
考虑编队卫星为近距离编队,且参考星运行于近圆轨道,则有
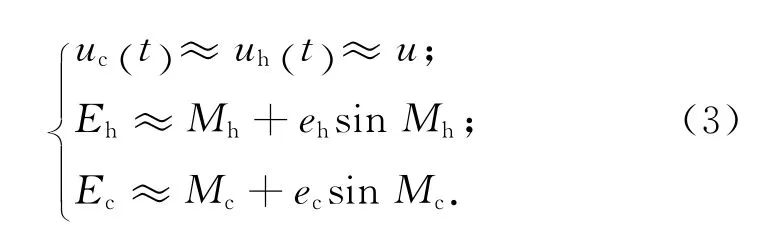
将式(1)、(3)代入式(2),略去二阶角度小量,整理可得
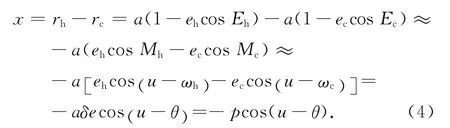
其中,相对偏心率矢量
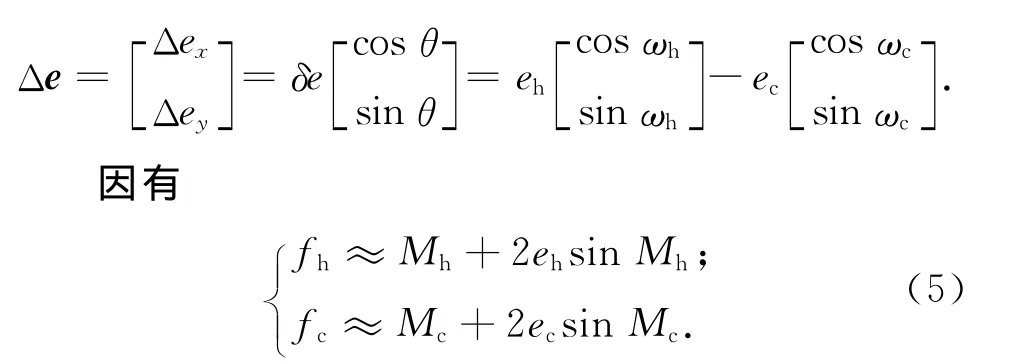
同理推导可得
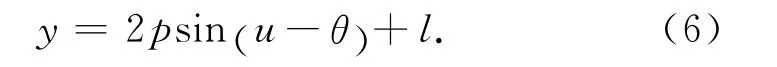
式中:l为伴飞轨迹中心与参考星的距离,且l=a(Δλ+ΔΩcosic);Δλ= (ωh+Mh)-(ωc+Mc)为伴随星与参考星的平纬度幅角之差。
整理式(2)的第三式,得
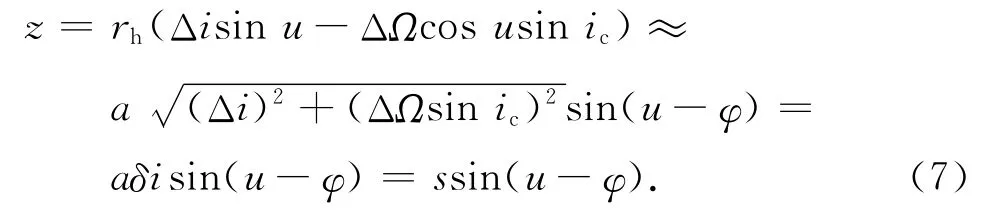
其中,相对轨道倾角矢量
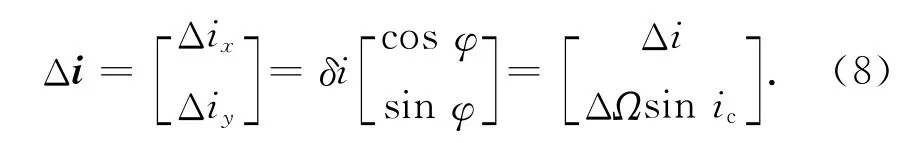
综合上述推导,用e/i矢量方法表示的编队运动学方程为
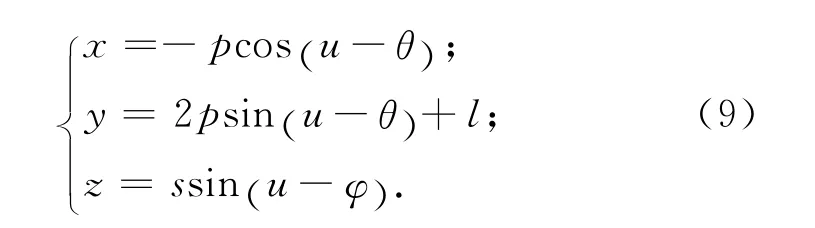
式中:p为轨道平面内投影椭圆短半轴,确定相对轨道的基准轨道平面内模态尺度;s为垂直于轨道平面方向运动振幅,确定相对伴随轨道的基准轨道平面外模态尺度;l为绕飞轨迹中心与参考星的距离;θ为编队绕飞椭圆在目标轨道平面内的初始相位,确定相对伴随轨道初始状态;φ确定相对轨道在轨道坐标系中取向。
2 InSAR卫星测量约束
2.1 基线定义
当接收天线和目标点不在同一距离向平面内时,成像处理中可经方位向聚焦压缩到距离向平面上,这等同于经典的正侧视情形。根据测量的需要,将干涉基线沿航迹和切航迹两个方向上分解为水平基线和垂直基线,定义如图2所示[5]。图中:o为参考星质心;S2,S′2分别为绕飞星及其在xoz平面投影;oS′2,B分别为垂直基线及其在oy轴上的投影;oB为航向基线(即水平基线);α为oS′2与oz轴的基线倾角;视线在xoz平面内;θL为下视角;S为参考星在视线上的投影;oS为有效垂直基线。
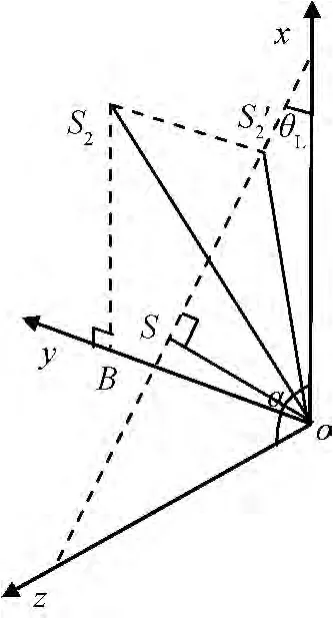
图2 干涉基线分解Fig.2 Decomposition of interference base line
设绕飞星在o-xyz系中的坐标为(x,y,z),则水平基线、垂直基线有效垂直基线可表示为
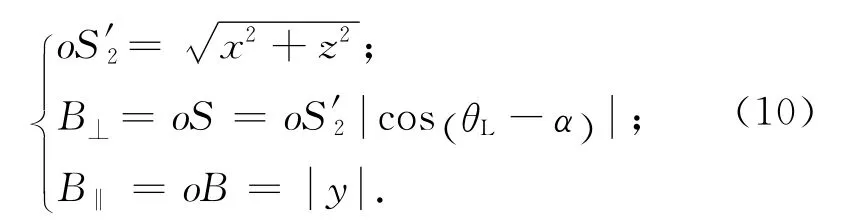
由式(10)可知:因参考星与伴飞星在整个卫星编队的运行过程中不断运动,导致两者间的水平基线、垂直基线和有效垂直基线随时间不断变化。若基线长度在可成像的基线长度范围内,则可被成像处理接受;否则,将会给接收信号的图像处理带来困难。最坏情况下,基线的长度超出临界基线将使两幅卫星天线收到的信号不再相关,干涉后不能获得所需的图像。因此,选择InSAR卫星的编队构形时,应充分考虑测量约束,确保卫星的每轨可用测量时间最长或全球的纬度覆盖范围最大。
2.2 干涉约束
由文献[11]可知,InSAR卫星在测量过程中存在最佳有效垂直基线,其长度与天线频率、星地距离等因素相关。卫星飞行过程中,无法确保垂直基线长度为定值,但在以最佳基线为中心的一个范围内,InSAR卫星干涉成像的效果可满足测量任务精度需求。
基于上述概念,综合InSAR卫星系统测量干涉和卫星安全性等要求,InSAR卫星编队构形的优选约束可表示为
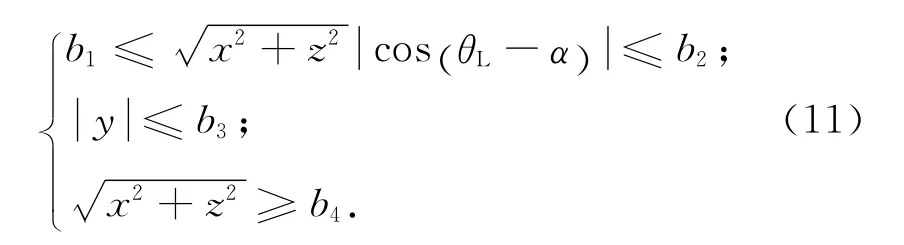
式中:b1,b2,b3,b4分别为有效垂直基线的最小值、最大值,水平基线的最大值,以及两星平面外最小距离。
编队卫星因受J2摄动等外界干扰力的影响,卫星的相对构形会发生改变,无法保持初始构形,从而可能导致两星相对距离太近,对编队卫星的安全性造成威胁,故需要通过编队控制以避免碰撞[12]。为减少编队控制次数,可在编队构形优化设计中加入构形安全性稳定条件,即要求编队构形在控制周期范围内任意时刻均可满足式(11)中第三式的约束,可修改为
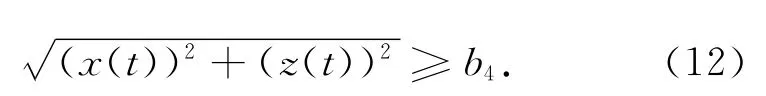
式中:t为队构形保持周期。
3 InSAR卫星构形优选方法
根据文献,德国TanDEM_X卫星任务的主星运行于太阳同步轨道,采用Helix轨道构形(编队卫星等长半轴、等倾角)。考虑目前国内外低轨卫星多运行于太阳同步轨道,故给出的InSAR卫星构形优化方法是针对太阳同步轨道的InSAR任务。
当编队卫星均运行于太阳同步轨道时,满足Δi=0,即式(9)中的φ=90°。则式(9)可变为
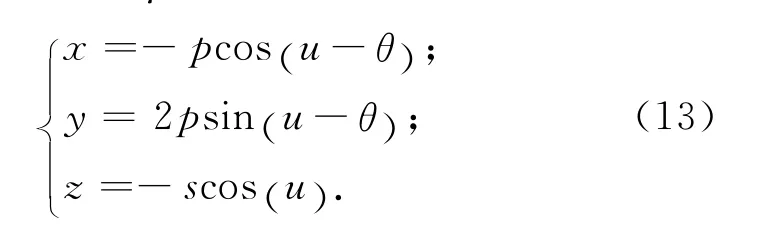
为满足InSAR卫星测绘任务,同时符合InSAR系统测量干涉要求,需分别设计高、低纬度编队构形。
3.1 构形设计
当编队卫星运行于太阳同步轨道时,编队卫星的轨道半长轴相等,则两颗卫星轨道能覆盖的最高纬度相同,可根据轨道倾角算得。
定义低纬度编队构形最大可覆盖的地面纬度为Φmax,考虑卫星编队构形的对称性,如构形可实现北半球的纬度覆盖最大,则南半球的覆盖纬度同样达到最大值,因此在构形设计时只需以半球的覆盖为对象即可。
在载荷成像条件及构形安全性等约束条件b1~b4,θL,t已知的条件下,本文算法以地面纬度覆盖最大为优化目标。优化问题可表示为
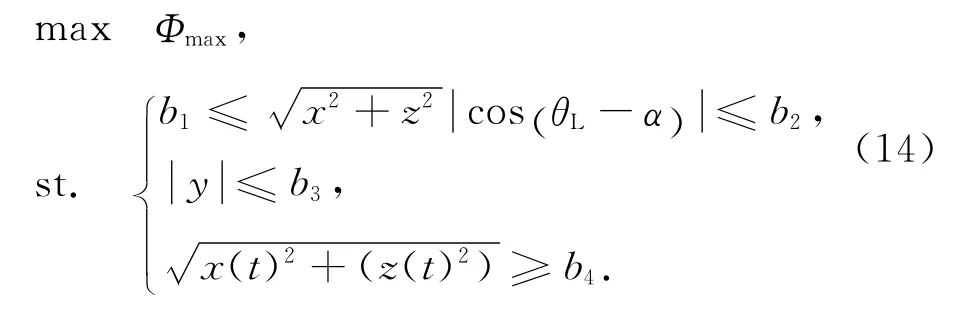
优化算法以Φmax为目标函数,θ作为待优化变量。初始时刻取Φmax为轨道可覆盖的最高纬度,当θ在0°~360°变化时,分别计算Φmax,Φmin对应的p,由式(11)的第二式选取满足条件的p值;当Φmax,Φmin,θ,b1,b2已知时,可算得s1,s2,若满足s1>s2,且符合编队安全性约束,记录p,s,θ值,循环结束,此时记录的p,s,θ即为最佳构形参数,可覆盖的最大纬度范围为Φmax;若条件不满足,Φmax=Φmax-1,重复上述过程。
3.2 构形设计流程
由本文的构形优化方法和式(11)~(13),低纬度优化设计流程如图3所示。对高纬度编队飞行,其构形设计流程与低纬度类似。
4 数值仿真
取主星的轨道六要素为a=7 171.23km,e=0.001 5,Ω=10.00°,i=98.598°,近地点角距ω=60.00°,平近点角M=30.05°;InSAR卫星编队构形需满足的约束条件为b1=1 000m,b2=1 500m,b3=1 000m,b4=350m,θL=38°,t=7d。用本文的构形优化算法所得高、低纬度的构形参数见表1,关键参数如图4~7所示。图中:实线表示卫星在轨期间满足测绘条件的区域;虚线表示卫星的基线及编队构型等参数变化。
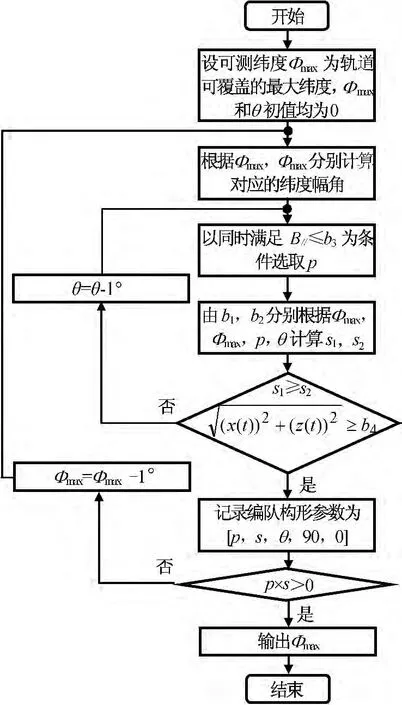
图3 低纬度编队飞行构形优选流程Fig.3 Flowchart of low latitude optimal formation design
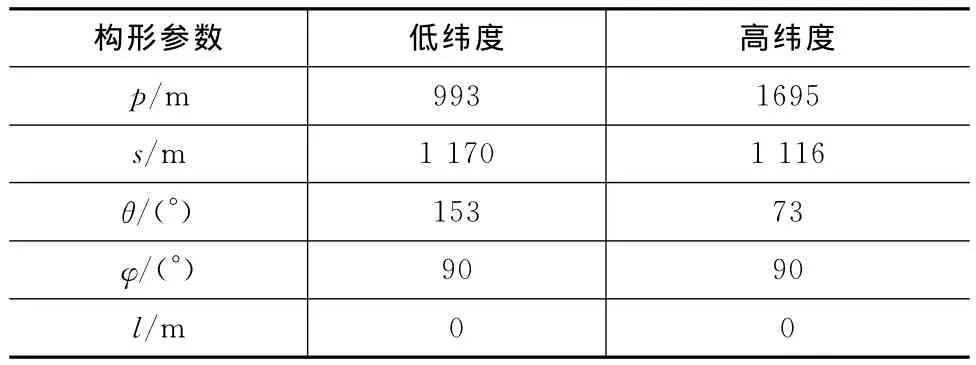
表1 高、低纬度构形参数Tab.1 Parameters of low/high formation configuration
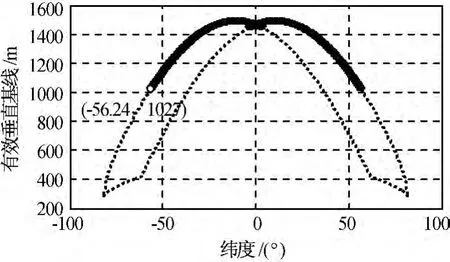
图4 不同纬度的低纬度构形有效基线Fig.4 Effective base line valued by latitude of low latitude formation flying
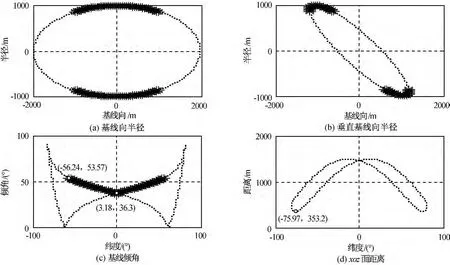
图5 低纬度构形、基线倾角和安全距离Fig.5 Formation configuration,base line inclination and safe distance of low latitude formation
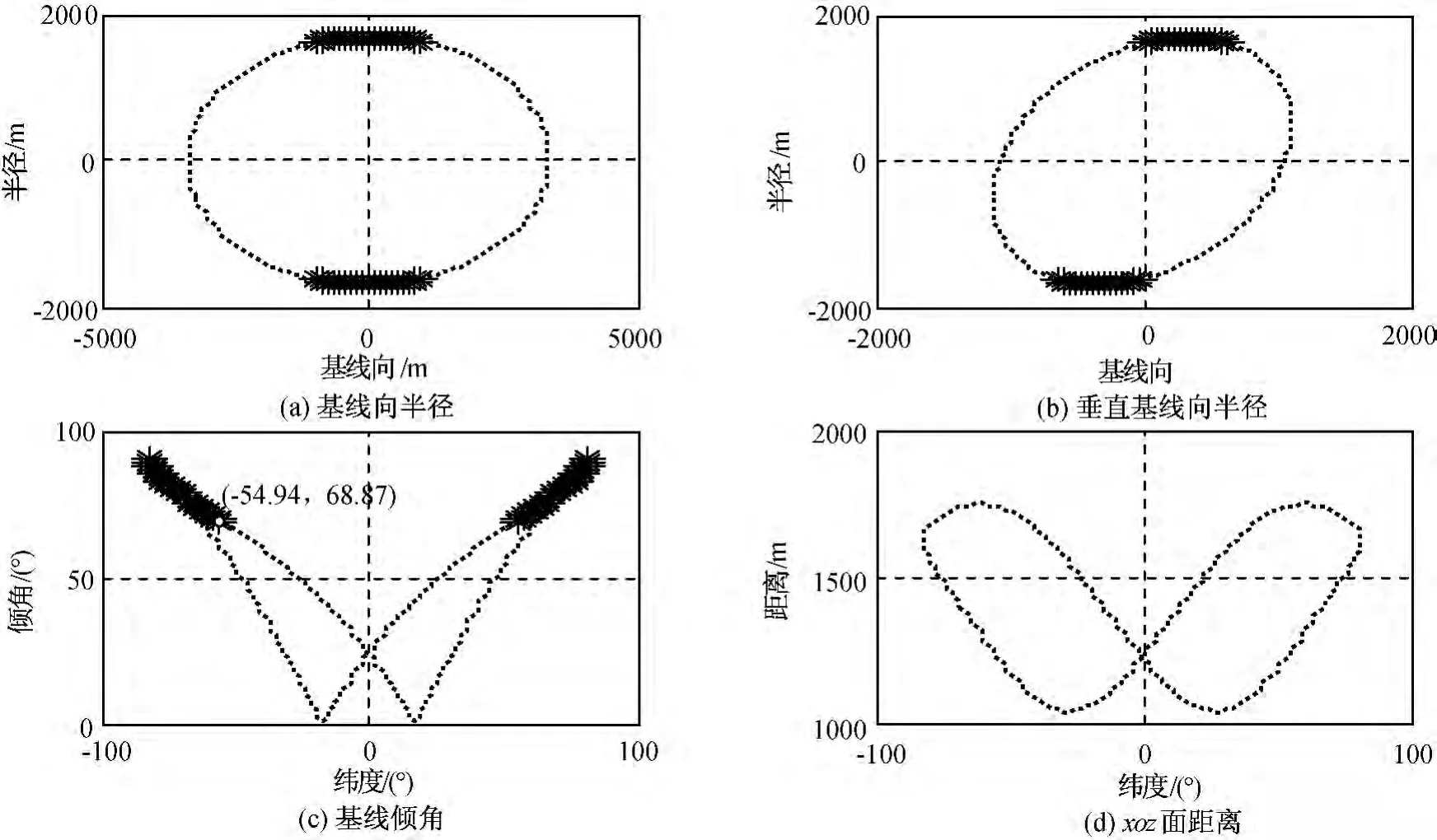
图6 高纬度构形、基线倾角和安全距离Fig.6 Formation configuration,base line inclination and safe distance of high latitude formation
根据仿真结果可得以下结论:
a)满足基线长度约束的高、低纬度的构形分别可覆盖南北纬54.94°~81.4°、南纬56.24°~北纬56.24°的区域,两者联合可实现南纬81.4°~北纬81.4°的纬度覆盖;
b)在无摄动情况下,高、低纬度的构形在xoz面内最小距离约353.2m,满足编队卫星安全距离350m的条件要求;
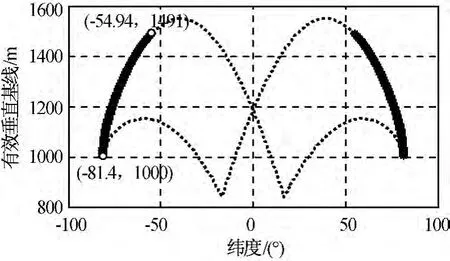
图7 不同纬度的高纬度构形有效基线Fig.7 Effective base line valued by latitude of high latitude formation flying
c)低纬度构形基线倾角较小(35°~55°),高纬度构形则基线倾角接近90°,这是因为基线倾角与编队的侧向运动密切相关,而当编队卫星的倾角一致时,在极地附近侧向位移趋近于零,高纬度基线倾角则必然趋近于90°。
为验证所选构形参数的构形长期安全性,考虑J2摄动,分别对高、低构形进行仿真,所得7d内编队构形的变化分别如图8~11所示。图中:实线为卫星在轨期间满足测绘条件的区域;虚线为卫星在轨第1d时的基线及编队构形等参数;粗实线为卫星在轨第d天的基线及编队构形等参数。
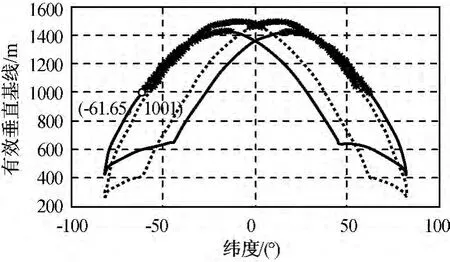
图8 不同纬度的低纬度构形有效基线Fig.8 Effective base line valued by latitude of low latitude formation flying
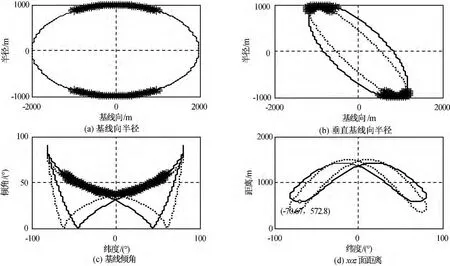
图9 低纬度构形、基线倾角和安全距离Fig.9 Formation configuration,base line inclination and safe distance of low latitude formation
由仿真结果可知编队构形7d内的变化趋势为:
a)低纬度编队可测绘区域逐渐向高纬度漂移,高纬度可测绘区域逐渐缩小并向低纬度漂移;
b)7d内,虽然高纬度构形xoz面内的最小相对距离变小,低纬度构形xoz面内的最小相对距离变大,但均可保证350m的安全距离,验证了构形选择算法中长期安全性约束的有效性;
c)随着编队构形的漂移,低纬度构形的基线倾角逐渐增大。
根据仿真结果可发现,本文设计的InSAR卫星编队构形优化算法方法可实现预期目标,能设计获得满足有效基线、构形长期安全性等约束条件的构形,满足对地测绘区域最大的任务要求,具有工程可行性。
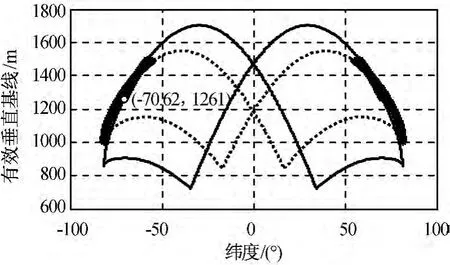
图10 不同纬度的高纬度构形有效基线Fig.10 Effective base line valued by latitude of high latitude formation flying
5 结束语
本文给出了一种可同时满足InSAR卫星测量多约束要求的编队构形优化方法。根据相对轨道根数,在编队卫星近距离假设条件下,推导了基于e/i矢量的编队卫星相对运动学方程。在此基础上,充分考虑有效基线、安全距离等条件对于InSAR卫星成像的约束,根据太阳同步轨道InSAR卫星编队飞行特点,给出了满足干涉成像及编队构形安全性要求的编队构形优化算法。无摄动和有J2摄动的两种数学模型仿真验证了该编队构形优化方法的有效性,可实现最大观测区域的对地成像,符合设计要求,对InSAR卫星编队飞行控制和工程实践有参考意义。
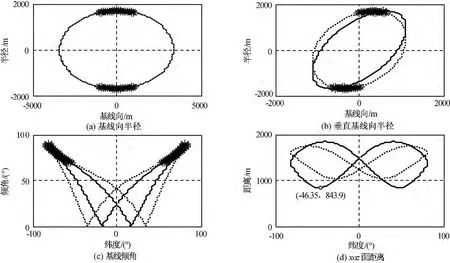
图11 高纬度构形、基线倾角和安全距离Fig.11 Formation configuration,base line inclination and safe distance of high latitude formation
[1] 郗晓宁,王 威,高玉东.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003:252-262.
[2] 何 锋,梁甸农,董 臻.主星带伴随小卫星编队SAR系统干涉测高精度与编队构形设计[J].宇航学报,2005,26(4):455-460.
[3] 李真芳,王 彤,保 铮,等.同时地形高程测量和地面运动目标检测的分布式InSAR最优编队构形[J].宇航学报,2004,25(6):642-647.
[4] 郝继刚,张育林.SAR干涉测高分布式小卫星编队构形优化设计[J].宇航学报,2006,27(4):654-658.
[5] 刘 磊.星载干涉式合成孔径雷达卫星编队构形设计[D].长沙:国防科学技术大学,2004.
[6] 张晓玲,曾 斌,黄顺吉.分布式卫星的环绕对In-SAR测高精度的影响[J].电子与信息学报,2004,26(1):159-164.
[7] 杜耀珂,阳 光,王文妍.InSAR卫星编队构形的e/i矢量设计方法[J].上海航天,2011,28(5):8-13.
[8] 曾国强,张育林.编队飞行队形设计一般化方法[J].中国空间科学技术,2006,27(4):21-25.
[9] EBERHARD G,Autonomous formation flying for the PRISMA mission[J].Journal of Spacecraft and Rockets,2007,44(3):671-681.
[10] 杨 宇,韩 潮.编队飞行卫星群描述及摄动分析[J].中国空间科学技术,2002,23(2):15-23.
[11] RODRIGUEZ E,MARTIN J M.Theory and design of interferometric synthetic aperture radars[J].IEE Proceedings-F:Radar and Signal Processing (0956-375X),1992,139(2):147-159.
[12] 张玉锟,戴金海.考虑J2项摄动的卫星编队飞行[J].国防科技大学学报,2002,24(2):6-10.
