基于Worldview-2影像的林木冠幅提取与树高反演

孙 华，鞠洪波，张怀清，凌成星

（1. 中南林业科技大学 林业遥感信息工程研究中心，湖南 长沙 410004；2. 中国林业科学研究院资源信息所，北京 100091）

基于Worldview-2影像的林木冠幅提取与树高反演

孙 华1,2，鞠洪波2，张怀清2，凌成星2

（1. 中南林业科技大学 林业遥感信息工程研究中心，湖南 长沙 410004；2. 中国林业科学研究院资源信息所，北京 100091）

以湖南省攸县黄丰桥国有林场杉木人工林为例，探讨林木冠幅提取与树高反演方法研究。基于Worldview-2影像，采用均值漂移分割算法开展样地内杉木冠幅信息提取。通过设置不同分割尺度确定最佳的冠幅分割参数为hs=10，hr=6，M=20。对提取的冠幅边界进行平滑处理，利用平滑后的影像冠幅与实测树高，分别建立了冠幅树高曲线估计模型和非线性联立方程组反演模型。其中以树高作为哑变量，建立的影像冠幅树高非线性联立方程组模型的拟合效果最佳，模型决定系数R2为0.899，模型的变动系数（CV），平均百分标准误差（EMPSE）均在10%以内，是树高反演的一种有效手段。

林业遥感；林木冠幅；杉木人工林；图像分割；均值漂移算法；非线性联立方程组

进入21世纪，随着高空间分辨率遥感影像不断涌现，遥感技术在林业中的应用由最初的森林类型识别和信息提取，向更加精细的方向发展，已经开始用于森林参数提取研究。树高是一个重要的森林参数，是森林蓄积量和地上生物量估测的一个重要指标。对于多光谱影像而言，通过提取影像各波段反射率、植被指数、纹理因子及其衍生变量的散点图，采用空间统计学或逐步回归技术提取与树高相关性高的波段或变量，建立回归模型来反演树高是比较常见的方法[1-4]。近年来，冠幅胸径模型以及冠幅树高模型的研究受到了国内外的关注，已有的文献研究表明冠幅与树高、胸径有着良好的数学关系，林木位置和树冠信息提取成为高分辨率遥感影像研究的焦点[5-6]。为了从影像上快速识别和分析冠幅特征，并将冠幅信息从遥感影像数据中分离并提取出来，面向对象的分割技术被认为是一种有效的方式[7-9]。近年来随着商业遥感分析软件eCognition的应用，面向对象的遥感影像分析方法越来越受到研究者的关注。国内外学者在图像分割方面开展了大量的研究，借助各种理论提出了上千种分割算法。现已提出的分割算法都是针对具体的问题，并没有一种适用于所有图像的通用分割算法。对于树冠信息提取而言，研究的算法主要侧重于局部最大值法，基于轮廓的方法，模板匹配法，区域增长法，分水岭算法等[10-13]。

论文以Worldview-2影像为数据源，采用均值漂移算法（Mean Shift algorithm）开展杉木树冠信息提取与树高反演研究。首先从影像中提取冠幅的边缘特征，通过图像分割的方式确定最佳的冠幅提取尺度。同时开展地面样地调查，进行每木检尺，记录每棵树的位置、胸径、树高、冠幅长度（东西和南北）、以及林分郁闭度等信息。分析调查数据中实测冠幅与影像提取冠幅之间的相关性。结合实测树高与冠幅的关系，最终建立杉木人工林影像冠幅树高联立方程组反演模型。

1 材料与方法

1.1 研究区概况

湖南省攸县黄丰桥林场介于113°04′～113°43′E，27°06′～ 27°24′N 之间。东北部与江西的莲花、萍乡交界，东南与茶陵县接壤，西北部与株洲、醴陵毗邻。全场地貌以中低山为主，境内最高海拔1 270 m，最低海拔115 m，坡度介于20～35°之间。林场地处中亚热带季风湿润气候区，年均气温17.8℃，平均无霜期为292 d，年均降水量1 410.8 mm。全场现有林地面积10 122.6 hm2，活立木蓄积879 705 m3，其中有林地蓄积879 688 m3，占活立木蓄积99.99%，四旁树蓄积17 m3，仅占0.01%。林场的森林覆盖率为86.24%。树种主要以杉木Cunninghamia lanceolata(Lamb.) Hook、松类Pinusspp为主，其中杉木面积3 197.6 hm2，占用材林面积89.9%，蓄积593 738 m3，占96.56%，全部为人工造林[14]。

1.2 均值漂移算法

均值漂移算法（Mean Shift）是一种是非参数估计密度函数的方法，使每一个点通过有效的统计迭代“漂移”到密度函数的局部极大值点。算法思想最初由Fukunaga（1975）等人[15]在一篇关于概率密度梯度函数的估计论文中提出来的，Cheng（1995）对算法进行了推广，定义了核函数以及设定了一个权重系数，扩大了算法的适用范围。Comaniciu（2002）等人[16]证明了算法的收敛性，将Mean Shift算法运用到图像的特征空间分析中。Mean Shift算法本质上是一个自适应的梯度上升搜索峰值的方法，近年来，Mean shift算法在图像平滑、分割以及视频跟踪等领域获得了非常成功的应用效果。并逐步应用于中高分辨率遥感影像的实现遥感影像的多尺度分割，在分割参数控制及稳定性方面研究成果颇多，有关Meanshift算法的相关数学推导见参考文献[16]。

1.3 建模方法

本研究拟采取曲线估计和近代统计学中联立方程组法构建Worldview-2影像冠幅树高模型[17]。为了表达方便，用HT代表实测树高，CW代表实测冠幅，PCW代表提取的影像冠幅。联立方程组模型构建具体步骤如下：

（1）通过地面实测样木数据，构建HT-CW模型；

（2）建立基于分割算法提取的林木冠幅与实测冠幅（CW-PCW）模型；

（3）HT-CW模型与CW-PCW模型联立，建立联立方程组模型。

1.4 模型评价

利用确定系数R2、估计值的标准差（Standard Error of Estimate，SEE）、变动系数（Coeff i cient of Variation，CV）和平均百分标准误差（Mean Percent Standard Error，MPSE）4个评价指标对模型进行检验。

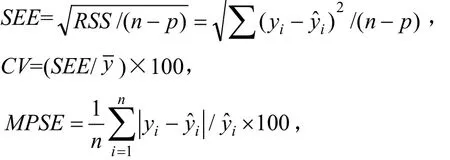
式中，yi表示实测值，yˆi表示预测值，y表示实测值的均值，p为模型参数个数。

2 结果与分析

2.1 冠幅提取分析

树木的冠幅信息在图像上所表示同质范围相对较小，要想在遥感影像上准确提取冠幅信息，分割尺度是一个必须要考虑的问题。对于Mean Shift而言，通过控制核的带宽参数（hs，hr），有效的将同质区域影像分割到同一对象块中，最后利用最小区域面积（M）参数逐步实现影像的多尺度分割。考虑到单棵树的树冠面积相对较小，在保持空间特征带宽hs与颜色特征带宽hr不变（hs=10，hr=6）的情况下，逐步减少最小区域面积参数M的值，发现随着最小区域面积值的减少，分割出来的斑块数量呈几何级数增长（图1），而且分割效果不佳，出现了过分割现象。

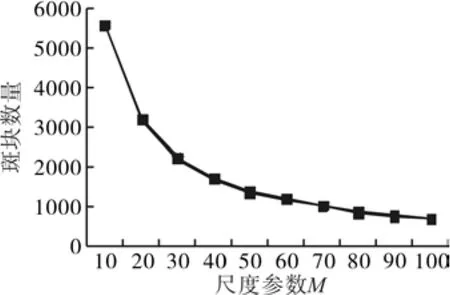
图1 斑块数量与最小区域面积尺度M的相关曲线Fig.1 Relation between plaque numbers and minimum area scale parameter

图2 （hr=6，M=20）和图3（hs=20，M=20）分别表示在两个参数固定不变的情况下，斑块数量随空间尺度和光谱尺度变化的关系，从中可以得知，两者的曲线的变化趋势基本一致，尺度越大，所生成的斑块数量越少；从两条曲线的比较来看，在最小区域面积保持不变的情况下（M=20），颜色特征尺度hr比空间尺度hs对斑块数量影响更敏感，随着尺度的增加，斑块的数量变化要大于空间尺度参数。

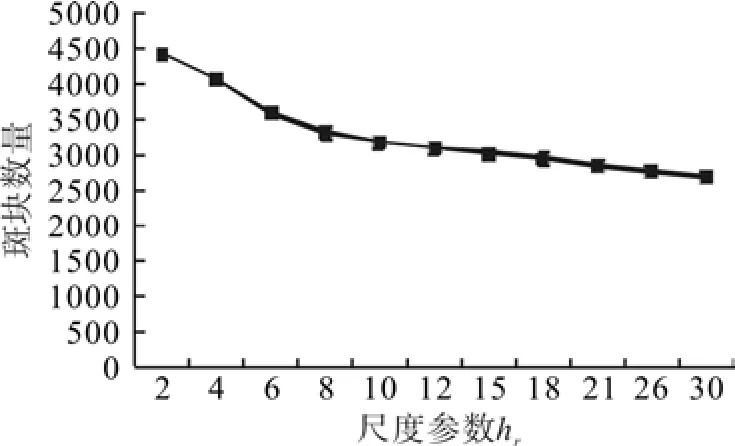
图2 斑块数量与尺度参数hs的相关曲线Fig.2 Relation between plaque numbers and scale parameter hs

图3 斑块数量与尺度参数hr相关Fig.3 Relation between plaque numbers and scale parameter hr

经过对上述3个分割参数的比较与分析之后，要达到准确提取杉木冠幅，确定最优的分割尺度，除了能准确显示冠幅边界信息之外，还需考虑通过分割之后的斑块不能太破碎，尤其是针对同质区域范围内的影像，分割结果尽可能保持图像的一致性，其次斑块数量要控制在一定的范围内，这样可以避免产生过分割现象，经过反复试验和比较，认为hs=10，hr=6，M=20对于研究区杉木冠幅提取具有较好的效果，共提取杉木有效冠幅样本227个，使用边界平滑算法对提取的冠幅进行平滑处理，效果如图4所示。

图4 Meanshift算法冠幅提取结果Fig.4 Extracted results of tree crows by using Meanshift

2.2 曲线估计模型

为了得到更为准确的模型，分别采用实测冠幅和影像提取的平均冠幅建立冠幅树高模型。从提取的227个杉木冠幅样本中，随机抽取157个样本作为建模数据，剩余70个样本作为检验数据。采用曲线估计中的11种模型进行冠幅树高建模，并选出最佳拟合模型，模型拟合结果如表1所示。从表中可以看出，利用实测冠幅信息建立的冠幅树高模型的拟合最佳曲线为二次方程，决定系数R2为0.52。利用影像提取的冠幅信息建立的冠幅树高拟合最佳曲线为幂函数模型，决定系数R2为0.36。

表 1 冠幅树高最佳曲线估计模型Table 1 Optimal evaluation models for crown-height

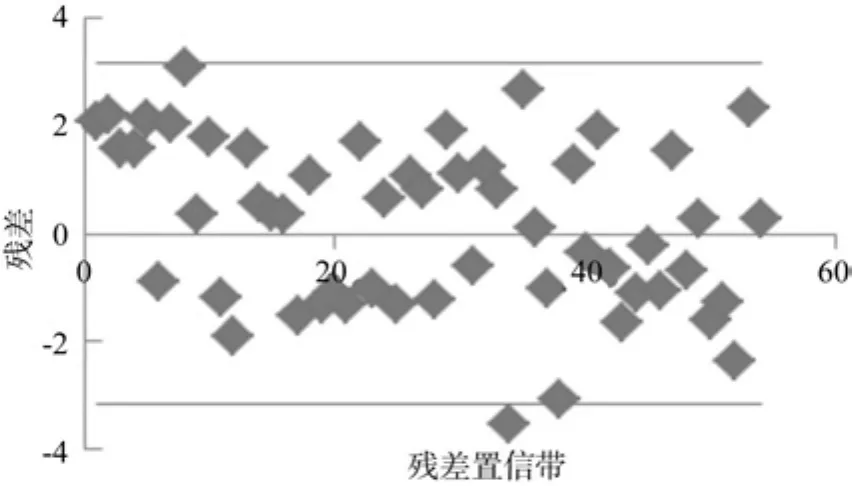
图5 实测冠幅树高模型残差分析Fig.5 Residual distribution of HT-CW model

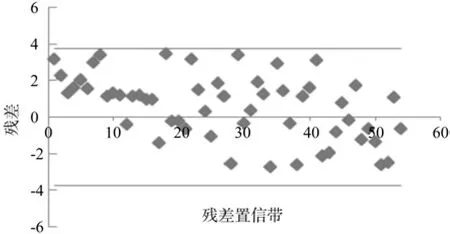
图6 影像冠幅树高模型残差分析Fig.6 Residual distribution of HT-PCW model

图5 和图6的残差分布结果表明2个模型检验数据的残差绝大部分都在置信带内 [-2σˆ，2σˆ]，残差点分布随机性较好，以0为基准线上下对称分布。从表2模型检验结果分析可知，利用影像提取的冠幅直接建立冠幅树高模型的精度低于实测冠幅树高建立的模型，因此利用影像冠幅直接建立树高的遥感反演模型的效果并不理想。

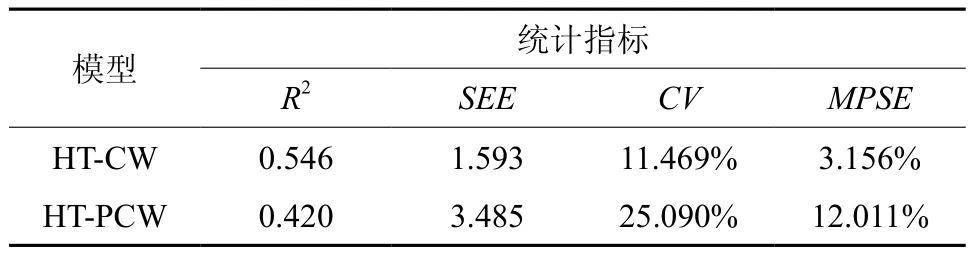
表2 冠幅树高模型检验结果Table 2 Examination results of regression models for crown-height

2.3 非线性联立方程组模型

实测冠幅与树高数据分析可知，冠幅与两者之间存在较好的二次方程的关系。如何建立影像上的冠幅与实测树高的反演模型呢？这需要从分析实测冠幅和影像提取冠幅之间的关系入手。首先，对多尺度均值漂移提取的227个平滑后的杉木冠幅与实测冠幅进行匹配，再建立曲线估计模型，从模型建立的情况来看，实测冠幅与遥感影像提取的冠幅存在良好的线性关系（图7），其决定系数R2=0.646。

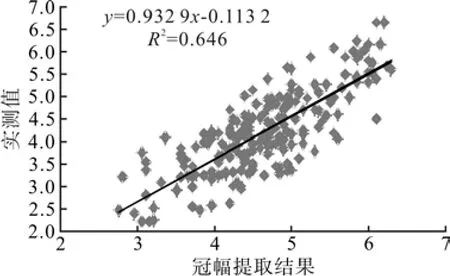
图7 冠幅提取结果与实测值拟合效果Fig.7 Observed values of tree crown width against estimated values

由上可知，实测冠幅与影像冠幅存在线性关系，而实测冠幅树高之间是二次方程的关系，是一种非线性关系。假定遥感影像冠幅没有度量误差，则可以通过实测冠幅建立影像冠幅与树高的非线性联立方程组反演模型。非线性联立方程组的严格数学模型和推导方法见唐守正等（2009），研究所建模型的分线性联立方程组运算通过ForStat软件得到。从提取的冠幅227个样本中，抽取157个样本进行构建非线性联立方程组反演模型，剩余70个样本用来做模型精度检验，所得冠幅/树高的非线性联立方程组如下：

式中，联立方程组的误差变量指的是CW和HT。CW的残差平方和为33.159，确定系数R2为0.642，H的残差平方和为619.904，确定系数R2为0.355。利用样本验证数据来检验非线性联立方程组模型预测值与实际观测值是否存在较好的线性拟合关系，分析残差的分布是否在置信带[-2σˆ，2σˆ]内。冠幅树高模型的检验结果如图8所示。

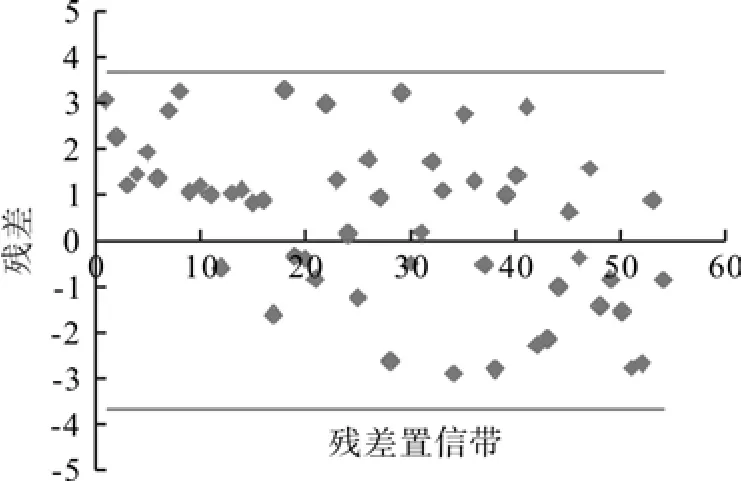
图8 非线性联立方程组模型残差分布Fig.8 Residual distribution of non-linear simultaneous model

从图8的残差分布可知，大部分验证数据的残差分布在置信带 [-2σˆ，2σˆ]内。从表3 验证数据的结果来看，验证数据所得的冠幅树高模型的决定系数0.419，与之前的冠幅与树高直接建立的反演方程相比，并没有得到明显改善。模型检验数据估计值的标准差（SEE）、变动系数（CV）、平均百分标准误差（MPSE）的统计结果与表3统计结果不差上下。从上述分析可知，假定影像冠幅提取的结果没有度量误差，建立影像冠幅与实测冠幅以及树高的联立方程组反演模型，没有达到预期的建模目标，需要对非线性联立方程组的建模因子做进一步的分析，提高模型的精度，使得模型解释更为合理。

表3 非线性联立方程组模型检验结果Table 3 Examination results of non-linear simultaneous equations

2.4 基于哑变量的非线性联立方程组模型

在考虑树高以及冠幅测量存在人为误差建立的联立方程组没有得到良好的效果时，应该考虑样地内林木树高的差异，将树高视为哑变量，进行数量化分级，建立基于哑变量的非线性联立方程组反演模型。样地实地调查的过程中，样地中林木树高差异较大，样地内最高的杉木为18.6 m，最低的仅为7.2 m，为了便于计算将树高分为4个等级，如表4所示。在ForStat软件中构建哑变量非线性联立方程组，将模型中所有参数的初始值设置为1，采用牛顿——拉格朗日方法进行计算。建模结果如下：

式中，CW表示实测平均冠幅，PCW表示影像上提取的冠幅长度，HT表示树高，树高的4个数量化等级表示如下：（1）当E1=E2=E3=0表示树高第一个等级（I），（2）当E1=1且E2=E3=0时表示第二个等级（II），（3）当E2=1且E1=E3=0表示第三个等级（III），（4）当E3=1且E1=E2=0表示第四个等级（IV）。模型中，CW的残差平方和为33.159，确定系数R2为0.642，H的残差平方和为97.535，确定系数R2为0.899。

表4 树高数量化分级Table 4 Quantitative hierarchy for DBH and HT

表5中模型检验结果表明，冠幅树高模型的拟合效果很好，决定系数R2为0.885。而且，模型检验数据估计值的标准差（SEE）、变动系数（CV）、平均百分标准误差（MPSE）的统计结果较非线性联立方程组有很大的改进，误差基本控制在10%以内。图9中残差点的分布随机性较好，绝大部分验证数据的残差分布在置信带 [-2σˆ，2σˆ]内。从上述分析可知，说明基于哑变量的非线性联立方程组建立影像冠幅与树高的反演模型效果十分理想。

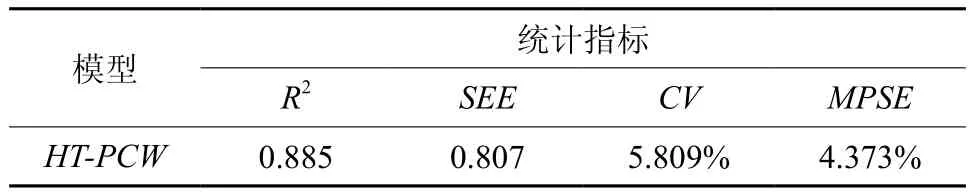
表5 哑变量非线性联立方程组模型检验结果Table 5 Examination results of non-linear simultaneous equations when dummy variable was used

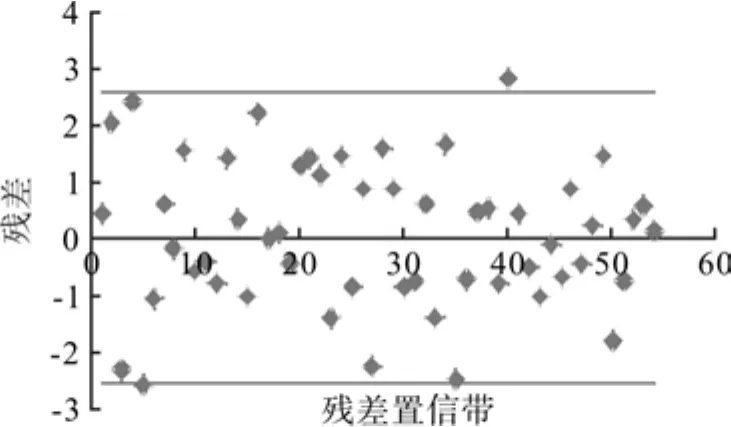
图9 哑变量非线性联立方程组残差分布Fig.9 Residual distribution of non-linear simultaneous equations when dummy variable was used

3 结论与讨论

以Worldview-2影像对研究对象，以地面调查样地为基础，首先利面向对象的图像分析方法开展杉木冠幅信息提取研究；其次，对提取的冠幅边界信息进行平滑处理，结合实测冠幅和树高建立联立方程组反演模型。对模型预测值与实际观测值是否存在较好的线性拟合关系进行了检验，分析了模型的残差分布，得出以下几点结论。

（1）面向对象的影像分割方法可以有效的提取杉木冠幅信息。研究运多尺度均值漂移分割方法对杉木冠幅信息进行提取。颜色特征尺度hr，空间尺度hs以及分割尺度（M）是多尺度均值漂移冠幅提取的关键，经过多次反复试验，确定最合适的分割参数为hs=10，hr=6，M=20，多尺度均值漂移提取的有效斑块数为227个，从斑块提取的有效性比较来看，多尺度均值漂移算法是提取林木冠幅的一种有效方法。

（2）建立了影像冠幅树高联立方程组反演模型。影像分割平滑后的冠幅与实测冠幅存在良好的线性关系，决定系数R2=0.646。同时，实测冠幅与树高最佳拟合曲线模型为二次方程。通过实测冠幅，建立了影像冠幅与树高的非线性联立方程组。其中，以考虑树高以及实测冠幅存在测量误差，且将树高作为哑变量建立的影像冠幅树高分线性误差变量联立方程组模型拟合效果最好，拟合效果比较理想，决定系数R2为0.899，模型的变动系数（CV）、平均百分标准误差（MPSE）在10%以内。模型的适用性检验表明，基于哑变量的非线性联立方程组模型的残差点分布随机性较好，以0为基准线上下对称分布，说明利用从影像提取冠幅进行树高的反演是可行的，可以为快速获取杉木人工林平均胸径、树高等森林参数提供方法与技术参考。

[1] 曾 涛,琚存勇,蔡体久,等. 利用变量投影重要性准则筛选郁闭度估测参数[J]. 北京林业大学学报,2010,32(6):37-41.

[2] Franklin S., Wulder M., Gerylo G. Texture analysis of IKONOS panchromatic data for Douglas-f i r forest age class separability in British Columbia[J]. International Journal of Remote Sensing ,2002, 22(13): 2627-2632.

[3] Vander Sanden JJ and Hoekman DH. Review of relationships between grey-tone co-occurrence, semivariance, and autocorrelation based image texture analysis approaches[J].Canadian Journal of Remote Sensing, 2005, 31(3):207-213.

[4] Jon Pasher, Douglas J. King. Multivariate forest structure modeling and mapping using high resolution airborne imagery and topographic information[J]. Remote Sensing of Environment,2010, (114): 1718-1732.

[5] Marshall D. D.,Gregory P.J.,Hann DW. Crown prof i le equations for stand-grown western hemlock trees in northwestern Oregon[J]. Canadian Journal of Forest Research, 2003, (33): 2059-2066.

[6] Turan Sönmez. Diameter at breast height-crown diameter prediction models for Picea orientalis[J]. African Journal of Agricultural Research, 2009,4(3):215-219.

[7] 覃先林,李增元,易浩若.高空间分辨率卫星遥感影像树冠信息提取方法研究[J].遥感技术与应用,2005,20(2):228-232

[8] 冯益明,李增元,张 旭.基于高空间分辨率影像的林分冠幅估计[J].林业科学,2006,42(5):110-113

[9] Pouliot D A, King D J, Bell F W,et al.Automated tree crown detection and delineation in high-resolution digital camera imagery of coniferous forest regeneration[J]. Remote Sensing of Environment. 2002,(82):322-334

[10] Leckie D G, Gougeon F A, Tinis S,et al. Automated tree recognition in old growth conifer stands with high resolution digital imagery[J]. Remote Sensing of Environment, 2005, (94):311-326

[11] 黄建文,鞠洪波,赵 峰,等. 利用遥感进行退耕还林成活率及长势监测方法的研究[J]. 遥感学报.2007,11(6):899-905

[12] 邓 广. 高空间分辨率遥感影像单株立木识别与树冠分割算法研究[J]. 北京中国林业科学研究院博士论文,2009,8-10

[13] Wang Le. A Multi-scale approach for delineating individual tree crowns with very high resolution imagery[J]. Photogrammetric Engineering & Remote Sensing,2010,76(4):371-378

[14] 孙 华,鞠洪波,张怀清,等. 三种回归分析方法在Hyperion影像LAI反演中的比较[J]. 生态学报,2012,32(24):7781-7790

[15] K. Fukunaga,L.D. Hostetler. The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition[J].IEEE Transactions on Information Theory,1975,21(1):32-40

[16] Dorin Comaniciu,Peter Meer. Mean shift:A robust approach toward feature space analysis[J]. IEEE Transaction on pattern analysis and machine intelligence,2002,24(5):601-619

[17] 唐守正,郎奎建,李海奎. 统计和生物数学模型计算(ForStat教程)[M].北京:科学出版社,2009,197-290.

[18] 李晓冬, 王雪峰, 贺 鹏. 林木冠层图像的分割方法研究[J].中南林业科技大学学报, 2013, 33(7): 40-44.

[19] 刘 刚, 张 雨, 臧 卓, 等. 多源遥感数据森林信息的提取和比较分析[J]. 中南林业科技大学学报, 2012, 32(10): 158-161.

Study on crown diameter extraction and tree height inversion based on worldview-2 data

SUN Hua1,2, JU Hong-bo2, ZHANG Huai-qing2, LING Cheng-xing2
(1. Research Center of Forestry Remote Sensing & Information Engineering, Central South University of forestry & Technology,Changsha 410004, Hunan, China; 2. Research Institute of Forest Resources Information Technique, Chinese Academy of Forestry,Beijing 100091, China)

By taking the Chinese fi r plantation in Huangfengqiao Forest Farm in Youxian county, Hunan province as the tested objective,the methods of tree crown width extraction and tree height inversion were studied. Based on worldview-2 data, the tree crown width information of the plantation was extracted by adopting mean shift segmentation algorithm. After setting a series of Image segmentation scale, the optimal crown width segmentation parameters’ values were determined, they arehs=10,hr=6,M=20.The extracted crown width border was smoothened, and the estimation model of tree crown=height curve and the inversion model of nonlinear simultaneous equations were respectively established based on the smoothed image’s crown width and measured tree height. Of them, the model of image tree crown-high nonlinear simultaneous equations set by taking tree high as the dummy argument had the optimal fi tting results,the model coeff i cient of determinationR2=0.899, the variation coeff i cient of modelCCVand the average percentage standard errorsEMPSEboth were less than 10%, so the last selected model is an effective means for tree height inversion of Chinese fi r plantation.

forest remote sensing; tree crown width; Chinese fir plantation; image segmentation; mean shift algorithm; non-linear simultaneous equations

S771.8

A

1673-923X(2014)10-0045-06

2013-12-21

国家“十二五”863课题：“数字化森林资源监测关键技术研究”（2012AA102001）；林业公益性行业科研专项（201104028）

孙 华（1979-），男，湖南隆回人，博士，讲师，研究方向为林业信息技术

张怀清（1973- ），男，湖南宁乡人，研究员，硕士生导师，主要从事林业可视化模型技术与湿地监测技术

[本文编校：吴 彬]