若干数学习题的知识性错解与分析

纪宏伟（江苏省如皋高等师范学校）

知识性错误是指学生对某些有关知识理解不清，运用不当造成的失误，主要类型有：数学概念理解错误，公式法则应用错误，定理性质应用错误，数学方法应用错误，在错误类型中，这类错误占据较大部分比例，可以说是学生丢分的“主源”.前车之覆后车之鉴，将常见、流行的知识性错解加以整理辨析，分类探源，可以帮助学生找出自己学习中的薄弱环节，使得学习重点突出，复习更加有针对性，方法更加有效.

一、概念理解错误

数学概念中的每一个定义、术语、符号乃至习惯用语，都有明确具体的含义.对于数学概念理解不透，内涵、外延把握不准都是导致解题出错的主要原因.

二、误用公式、法则

数学公式是解决数学问题的工具，是数学知识点的重要组成部分，数学中的公式、法则都由条件和结论组成.要应用结论，必须首先注意能使结论成立的条件.在数学学习中，记错了公式，或是记混了公式，或是忽视运算法则的适用范围，或是只局限于死记一些结论而不注意使结论成立的条件，往往会导致谬误，因此造成失分也是非常普遍的.

三、性质、定理应用错误

数学中的定理、性质是数学逻辑推理的依据，也是解决数学问题的工具，多数题目的设置就是以考查定理、性质的灵活应用为主要目的.由于对性质、定理把握不准、混淆不清，记错、用错、理解错误而导致各种错误屡见不鲜，频率较高.

例 6 已知 f（x）=ax2-c满足-4 ≤ f（1）≤ 1，-1 ≤ f（2）≤5，求 f（3）的取值范围.

评析：有学生这样处理：由题意1≤c-a≤4①，-1≤4a-c≤5②，f（3）=9a-c.一方面，①+②得0≤3a≤9，所以0≤9a≤27；另一方面①×4+②得3≤3c≤21，所以-7≤-c≤-1，故-7≤9a-c≤26.上述错误在于两次运用不等式的“可加性”性质导致不等式不等价变形，每用一次“可加性”，则范围就扩大一次，连续两次连用，使9a-c的变化范围不精确.正确解答是应用待定系数法，使 f（3）用 f（1），f（2）表示出

四、数学方法应用错误

高中阶段常用的数学方法有：配方法、换元法.待定系数法等等，这些方法是数学思想的具体体现，是解决问题的手段.对数学方法内涵不明确，或者对实施的步骤作法不熟悉，从而易导致数学方法应用错误.

例7 已知 x∈［0，1］时，f（x）=x2+ax+3-a>0恒成立，求实数a的取值范围.

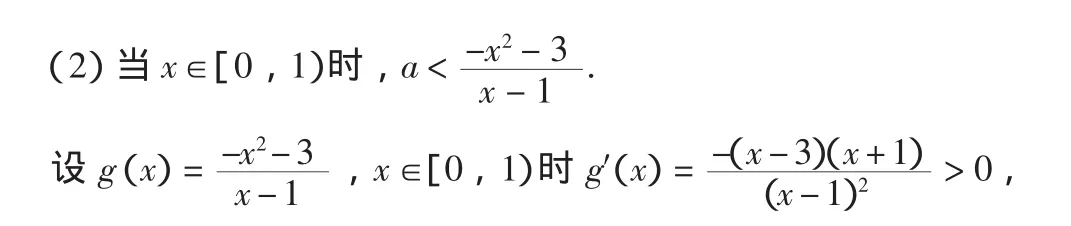
故 g（x）在［0，1）上单调递增，故 g（x）在［0，1）上的最小者g（0）=3，

从而a<3，即所求a的取值范围为（-∞，3）.

正如哲学家波普尔所说“错误中往往孕育着比正确更丰富的发现和创造因素”，解题错误也是我们学习中的宝贵财富，它暴露了我们的认知缺陷与不足，但同时也给我们提供了“治疗”的方向和纠错的机会.只要我们认真地追根溯源查找错因，深入反思总结，就可以克服知识弱点、盲点，填平知识缺陷，把知识掌握得更牢靠、全面、深刻，如此，错误重演的几率就可以降到最低了.的课上教师问一句，学生答一句，这种一问一答式让学生缺乏自主观察、提取信息、发现问题的机会，也使得知识揉捏过碎；有的教师有些拘泥于事前设计好的教案，面对学生课堂自动生成的有效契机不能灵活调控；有的教师对学生出现的问题引导不到位，常被学生牵着走；有的教师课堂评价语言零碎、随便，起不到激发鼓励学生的目的……我们就学学专家教给我们的“秘诀”吧：“两个解读（吃透）与教学经验、智慧有机融合，厚积薄发.吃透教材=学科知识+解读文本的智慧，吃透学生=学生知识+解读学生的智慧.智慧是由经验凝聚而成的.”

课堂教学评比结束后，笔者作为教研员，通过课后点评、与参赛教师、现场听课教师的三维互动，对全市数学教师进行了“在我们的课堂教学中如何实践课标新理念”为主题的培训活动.此次“打造优秀教研团队，提升教师专业素养，落实新课标理念，提高课堂有效性”的以课代训活动展现了教师对新课程理念、新课标、新教材的理解和把握，增进了校际之间、教师之间的交流与合作，全面提高了教师适应新课程、实践新课程、反思新课程的能力，有效地促进了教师专业化水平的提升，真正实现了用思想指导行动，用智慧启迪课堂.