非理想太阳帆受阴影影响的地球逃逸轨道探讨
2014-12-28钱航郑建华吴霞高东
钱航 郑建华 吴霞 高东
(1 中国科学院空间科学与应用研究中心,北京 100190)(2 中国科学院大学,北京 100190)
1 引言
太阳帆航天器以其不受燃料约束、可持续加速、能够形成很多新型轨道,而受到航天界的广泛关注和研究[1-5]。太阳帆能够从地球停泊轨道出发,通过改变帆的朝向来提供所需轨道速度方向推力,从而增加轨道能量实现逃逸出地球影响球。同样,太阳帆也能够完成其他行星逃逸轨道转移任务。
在19世纪60年代早期,Sands首先研究了太阳帆地球逃逸任务,使用模型较简单,并对仿真条件进行了高度简化[6]。2004年Macdonald 和McInnes对考虑地球遮挡的太阳帆地球逃逸轨道进行了优化设计,但只分析了锥形地影,采用的也仍是理想太阳帆[7]。国内,哈工大的史晓宁等[8]提出了一种太阳帆地球逃逸解析最优控制律,可使航天器在逃逸过程中轨道能量变化速率最大,然而没有考虑地影因素,推力模型也是理想模型。
本文研究考虑地影的非理想太阳帆地球逃逸轨道问题。根据太阳帆帆面的光学状况建立非理想太阳帆模型,并由日地关系建立三种不同的二维地影模型,采用能量变化率最大的逃逸控制律,以保证时间最优,可用于太阳帆地球逃逸轨道的设计,并为非理想帆面因素和地影遮挡因素的太阳帆控制提供参考。
2 太阳帆力学模型
2.1 动力学方程
由运载火箭将太阳帆航天器送入地球停泊轨道,太阳帆展开时的位置矢量和速度矢量分别为r0和v0,通过光压力的推进逃逸出地球影响球。采用二体模型,不考虑所有摄动力,只有地球引力和太阳光压力作用在太阳帆航天器上。建立如下坐标系:地球质心为中心o,日地连线指向地球方向为y轴,x轴与y轴垂直,如图1所示。太阳帆动力学方程为

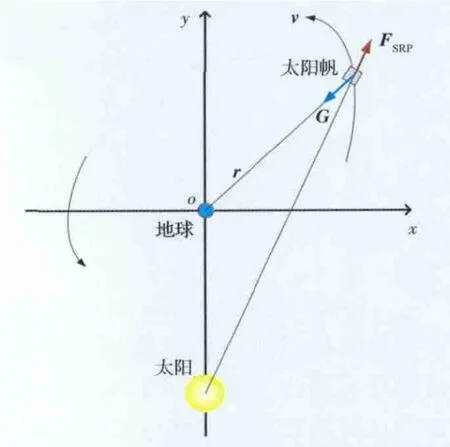
图1 太阳帆地球逃逸受力示意图Fig.1 Force vectors for earth departure
式中:r为从地心指向太阳帆质心的太阳帆位置矢量;G=为地球引力,μ是地球引力常数;FSRP为太阳光压力(Sun Radiation Pressure,SRP)。
2.2 帆面力学模型
此前文献中多采用理想太阳帆帆面模型,即帆面为平面,没有褶皱,太阳光子在帆面上是镜面反射[6-7],而实际上太阳帆的光压力模型很复杂。太阳帆的帆膜是正面镀铝,主要作用是镜面反射太阳光,但是由于帆面褶皱和鼓起将导致部分太阳光被漫反射,太阳帆还会吸收部分光子,帆膜反面镀铬主要作用就是为了散热。本文中的非理想太阳帆将考虑这些因素,以建立更为真实的太阳帆模型。
在与太阳距离为r时,太阳光压力大小可表示为
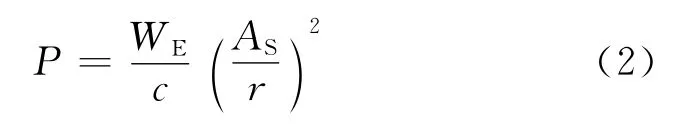
式中:WE是太阳常数,WE=1367 W/m2;c是真空中的光速,c=2.997 924 58×108m/s;AS为日地距离,AS=1.495 978 70×1011m。
Wright使用光学系数P={ρ,s,εf,εb,Bf,Bb},提出一种高阶力学模型,为帆面的材料特性建模[8-9],其中:ρ是反射系数;s是镜面反射因子;εf是太阳帆正面的漫反射系数;εb是太阳帆背面的漫反射系数;Bf是太阳帆正面的非朗伯系数;Bb是太阳帆反面的非朗伯系数。
基于上述光学系数的垂直帆面方向和平行帆面方向的太阳光压力如图2所示,Fn和Ft分别为
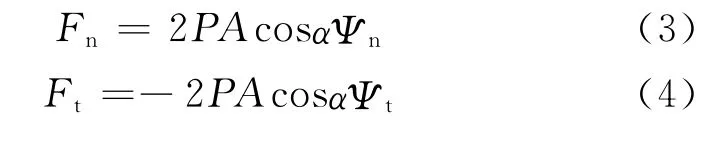
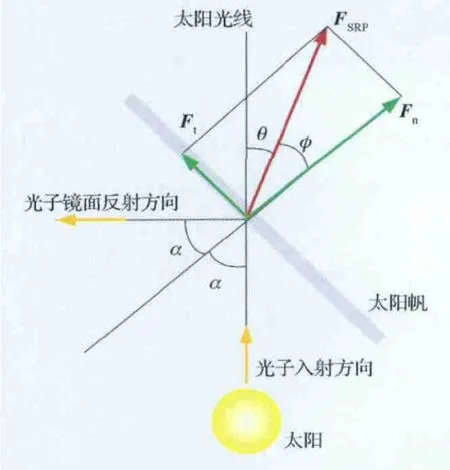
图2 非理想太阳帆模型Fig.2 Nonideal solar sail model
式中:A是太阳帆面积;α是太阳光线与帆面法线的夹角(称为锥角)。且

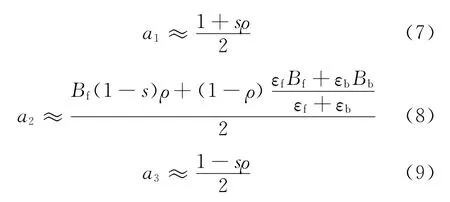

式中:m是太阳光压力方向上的单位矢量。
2.3 地影模型
讨论卫星光压摄动的地影模型有两种:圆柱形地影(如图3所示)和锥形地影(如图4所示),前者简单,后者精度较高。由于太阳半径约为地球半径的109倍,因此地影实为锥形。由于太阳帆逃逸轨道类似小推力逃逸轨道,是多圈螺旋线飞行,很可能会遇到多次进入地影区,这对太阳帆的逃逸轨道设计及姿态控制至关重要。
假设日地距离为恒定值,将大气衰减效应等效于地球半径增大20km[10]。在以下的讨论中需要用到如下一些符号和常量:RS为太阳半径,取值为696 000km;RE为地球赤道半径,加上大气衰减效应为6398 km;RSOI为地球影响球半径,大小为9.246 5×105km;d为地心到阴影锥顶的距离;σ为阴影锥的半锥角。
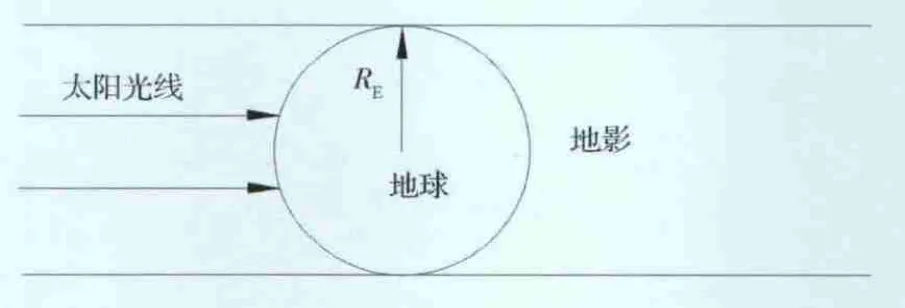
图3 圆柱形地影Fig.3 Cylindrical earth shadow model
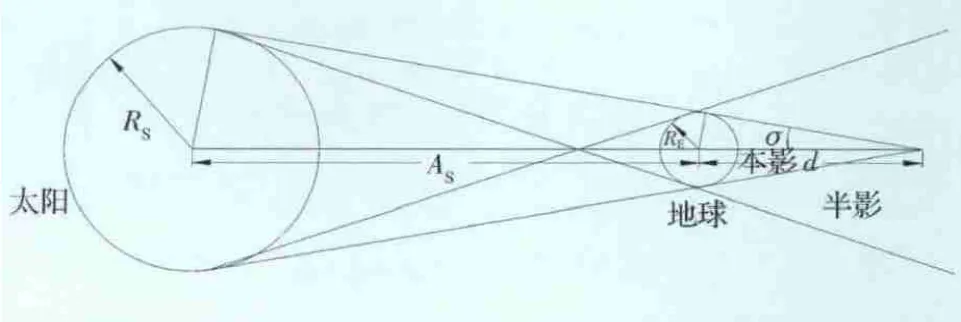
图4 锥形地影Fig.4 Cone-shaped earth shadow model
由图4中的几何关系可以得到
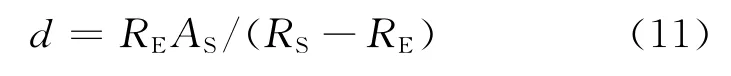
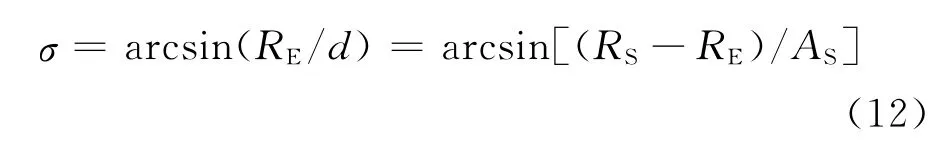
3 控制律设计
控制太阳帆的姿态就能够控制太阳光压力,从而逃逸出地球影响球。McInnes推导了一种最大化瞬时轨道能量增长率的局部最优控制律[10]。作用在太阳帆上主要有两种力:地球引力和太阳光压力。首先,用太阳帆速度矢量v点乘太阳帆动力学方程(1),并将地球引力项放入式(1)左侧,可以得到
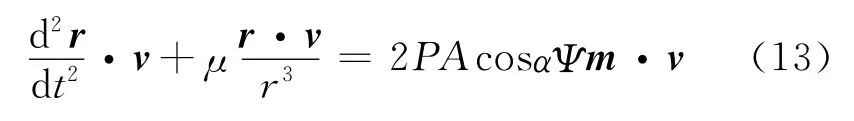
但是,式(13)右端项可以写成

实际上,式(14)右端项代表轨道总能量E 的瞬时变化率,可以写成
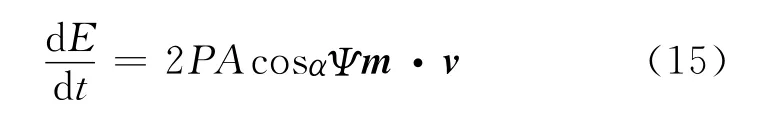
为了在轨道上的每一点使获得的能量最大化,调整太阳帆的锥角α使太阳光压力沿着速度矢量方向的分量最大化。定义太阳帆速度矢量与太阳光线矢量之间的夹角是γ,则
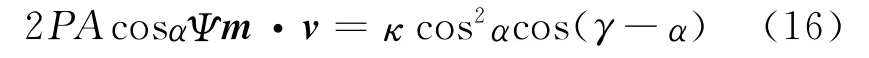
最大化轨道能量增长率也就是在给定的γ找出最优太阳帆锥角。
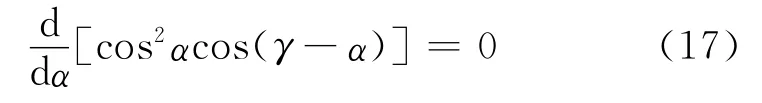
从而得到最优太阳帆锥角的表达式为
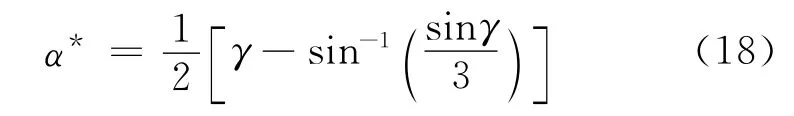
4 数值仿真
执行地球逃逸任务的太阳帆由于要进行复杂的变轨控制,所以其姿态控制方式不适合采用自旋稳定,必须采用三轴稳定控制。方形帆是比较适宜三轴稳定控制的[11-12],太阳帆的尺寸以200m×200m为宜,整个航天器质量225kg,采用工程中常见的材料就能制造满足任务需求的太阳帆。根据美国喷气推进实验室(JPL)的太阳帆哈雷彗星交会任务,方形太阳帆光学系数选择如表1所示。

表1 JPL方形太阳帆光学系数[11]Table 1 Opticalcoefficients for JPL square sail
4.1 模型对比分析
假设太阳帆航天器已经发射到8000 km、16 000km和24 000km 高度的圆形轨道,并从这个轨道出发逃逸出地球引力范围,进入日心转移轨道。仿真过程中对距离进行正则化处理,即设定1地球赤道半径=6378km。
表2和表3给出了非理想太阳帆和理想太阳帆在不同模型和不同释放高度逃逸出地球影响球的飞行时间。通过对比表2和表3可以看出,由于考虑了非理想帆面的因素,非理想太阳帆逃逸所需时间要多一些。之所以理想太阳帆在无地影模型下24 000km初始高度会比非理性太阳帆时间稍多,是因为在95d时理想太阳帆已经处在影响球边界附近但未越过边界,故需要再飞不到一圈才能真正越过边界。应该说,在相同条件下,还是符合理想太阳帆飞行时间更短的规律。表2和表3中本影模型的飞行时间比本影+半影模型稍长,同样是受到相位因素影响。

表2 非理想太阳帆在不同模型和不同释放高度逃逸出地球影响球的飞行时间Table 2 Departure time of nonideal sail
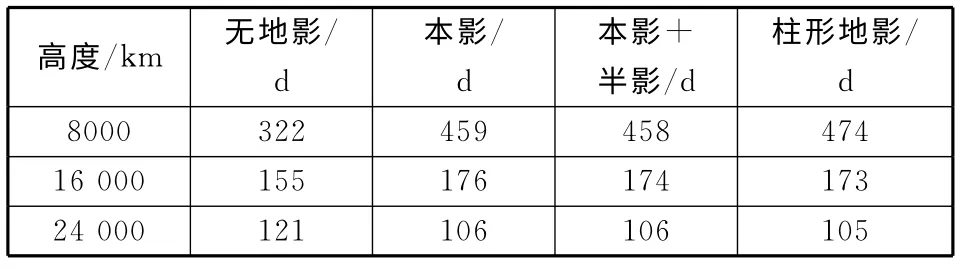
表3 理想太阳帆在不同模型和不同释放高度逃逸出地球影响球的飞行时间Table 3 Departure time of ideal sail
对比不同的地影模型可以看出,考虑地影比不考虑地影时太阳帆的飞行时间更长。同时,不同地影模型下,太阳帆的飞行时间也不相同。
4.2 太阳帆逃逸仿真分析
从16 000km 高度释放的非理想太阳帆在本影+半影模型下仿真得到逃逸出影响球需要184.48d,而太阳帆在地影的累计总时间3.56d,可见阴影时间还是不能忽略的。图5给出了考虑地影的非理想太阳帆地球逃逸段的全程轨迹,可以看出其轨道是多圈向外逃逸,并且整体轨道是垂直于太阳光线方向逐圈逃逸展开。
图6(a)是太阳帆到地心的距离图,红色虚线标出地球影响球的高度,蓝色窄条是地影时间窗口,可见每圈地影时间很小。太阳帆逐圈抬升轨道高度,最终逃逸出地球影响球。图6(b)是速度变化曲线,从速度的包络可以看出速度也是逐圈增大,最终达到逃逸速度。
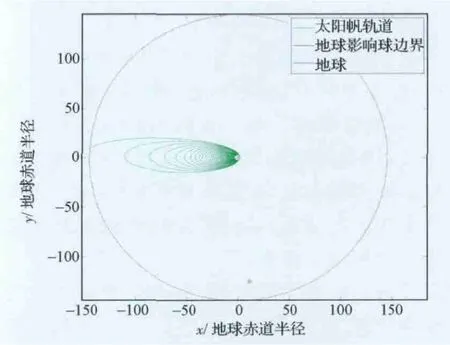
图5 考虑地影的非理想太阳帆地球逃逸轨道Fig.5 Earth departure trajectory of nonideal sail in the shadow

图6 太阳帆飞行位置和速度Fig.6 Time histories of sail position and velocity
图7(a)是每圈轨道的阴影时间,一直都是略有增加。地球阴影尽管每圈作用时间短,对每圈轨道的影响很小,但随着时间的推移,会对整体逃逸轨道和逃逸时间产生累积影响。图7(b)是光压推进时间,呈指数增加趋势。图7(c)的近地点高度也逐渐减小趋势,但最低高度是8 347.80km,太阳帆既不会与地球发生碰撞,也不用考虑大气阻力的影响。
通过以上仿真分析可以看出,作为无工质推进的新型航天器,太阳帆可以不借助运载火箭和自身的发动机逃逸出地球,这对质量有苛刻要求的航天工程来说具有重要意义。太阳帆帆面因素和地影遮挡因素对于太阳帆这种航天器来说,其影响是不可忽视的。太阳帆逃逸也有自身约束:由于推力小,则存在逃逸时间相对较长,处于地影时调姿困难等问题。
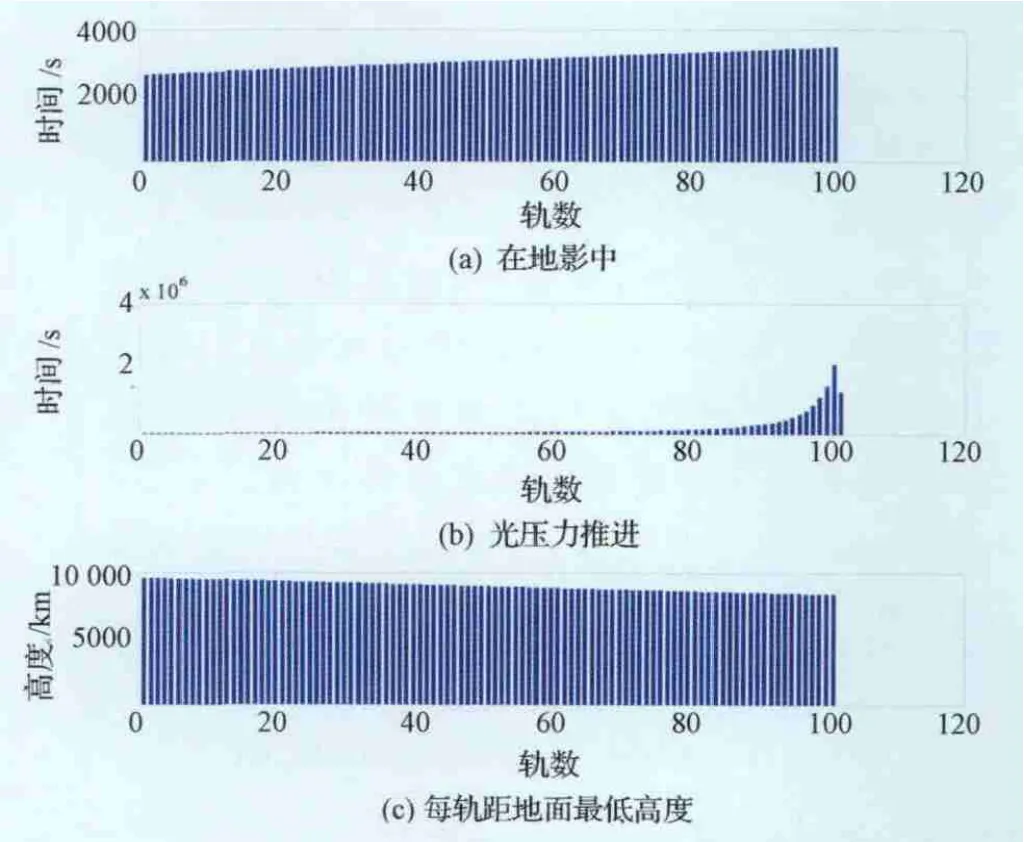
图7 每圈轨道参数变化图Fig.7 Time histories of departure parameters per orbit
5 结论
作为一种无需燃料的新型推进方式,太阳帆相对于其他传统航天器有更多的优势,采用太阳帆逃逸方式可以减轻对运载火箭能力的要求。目前,太阳帆逃逸轨道的研究多集中于控制律的设计,采用的太阳帆动力学模型都很简单,本文根据太阳帆帆面的光学状况建立非理想太阳帆模型,并由日地关系建立锥形地影模型,最后采用能量变化率最大的逃逸控制律,以保证时间最优。对比仿真数据可以看出,由于考虑了非理想帆面的因素,非理想太阳帆逃逸所需时间要多一些;考虑地影比不考虑地影时太阳帆所需逃逸时间更长;考虑不同地影模型同时受相位因素影响,太阳帆的逃逸时间也不相同。地球阴影尽管每圈作用时间短,对每圈轨道的影响很小,但随着时间的推移,会对整体逃逸轨道和逃逸时间产生累积影响。文中的逃逸轨道的平面特殊,在该平面内,太阳帆只能在赤道面内运动,并且忽略了黄赤夹角的存在,所以三维情况下的分析讨论应是进一步深入研究的方向。
(References)
[1]沈自才,张帆,赵春晴,等.IKAROS太阳帆的关键技术分析与启示[J].航天器工程,2012,21(2):101-107 Shen Zicai,Zhang Fan,Zhao Chunqing,et al.Key technology analysis and enlightenment of IKAROS solar sail[J].Spacecraft Engneering,2012,21(2):101-107 (in Chinese)
[2]钱航,郑建华,于锡峥,等.太阳帆航天器悬浮轨道动力学与控制[J].空间科学学报,2013,33(4):458-464 Qian Hang,Zheng Jianhua,Yu Xizheng,et al.Dynamics and control of displaced orbits for solar sail spacecraft[J].Chinese Journal of Space Science,2013,33(4):458-464(in Chinese)
[3]Y Tsuda,O Mori,R Funase,et al.Achievement of IKAROS-Japanese deep space solar sail demonstration mission[J].Acta Astronautica,2013,82(2):183-188
[4]Gong Shengping,Li Junfeng,Baoyin Hexi.Transfer trajectories design for a variable lightness solarcraft[J].Journal of Spacecraft and Rockets,2009,46(4):836-844
[5]Matteo C,McInnes C R.Generation of optimal trajectories for earth hybrid pole sitters[J].Journal of Guidance Control and Dynamics,2011,34(3):847-859
[6]Sands N.Escape from planetary gravitational fields by use of solar sail[J].American Rocket Society Journal,1961,31:527-531
[7]Macdonald M,McInnes C R.Realistic earth escape strategies for solar sailing[J].Journal of Guidance Control and Dynamics,2005,28(2):315-323
[8]史晓宁,李立涛,崔乃刚.太阳帆航天器地球逃逸轨道解析最优控制律[J].控制与决策,2013,28(2):253-258 Shi Xiaoning,Li Litao,Cui Naigang.Solar sail analytical optimal control law for earth escape transfer orbit[J].Control and Decision,2013,28(2):253-258(in Chinese)
[9]Wright J.Space sailing[M].Philadelphia:Gordon and Breach Science Publishers,1992
[10]张世杰,曹喜滨.卫星进/出地影位置和时间的计算算法[J].上海航天,2001,6:19-22 Zhang Shijie,Cao Xibin.Calculating method of satellite entry and exit positions and times through umbra/penumbra[J].Aerospace Shanghai,2001,6:19-22 (in Chinese)
[11]McInnes C R.Solar sailing:technology,dynamics,and mission applications[M].Chichester:Springer Praxis,1999
[12]罗超.太阳帆航天器轨道设计和姿态控制研究[D].北京:中国科学院空间科学与应用研究中心,2011 Luo Chao.Solar-sail spacecraft trajectory design and attitude control[D].Beijing:Center for Space Science and Applied Research,Chinese Academy of Sciences,2011(in Chinese)
