重力测量卫星KBR系统相位中心在轨标定算法

辛宁 邱乐德 张立华 丁延卫

（1 航天东方红卫星有限公司，北京 100094）（2 中国空间技术研究院，北京 100094）

1 引言

低低跟踪（SST-LL）重力测量卫星的核心载荷为K 频段测距（KBR）系统，该系统包括两副喇叭天线（分别安装在两颗卫星上），用于测量KBR 系统相位中心之间的距离及距离变化率，测量误差可达微米级［1］。由于重力场反演过程中需要的数据是两颗卫星质心之间的距离及距离变化率，因此还要确定两颗卫星在轨运行过程中卫星的质心与KBR 系统相位中心在视线方向上的距离。在地面研制阶段，KBR 系统相位中心与卫星质心的位置都是标定好的，但卫星在发射阶段中产生的振动、空间温度变化及电磁噪声等，都会使KBR 系统相位中心与质心间的相对位置发生改变，影响KBR 系统的在轨测量误差。为了反演高精度的地球重力场，进行KBR 系统相位中心在轨标定，进而为KBR 系统几何修正提供依据，具有重要的研究意义。

文献［2］提出了KBR 系统相位中心在轨标定的基本原理，将KBR 系统测量的距离及距离变化率与卫星旋转角的关系作为切入点，设计了卫星姿态机动规律，讨论KBR系统相位中心在轨标定的可行性。文献［3］从工程角度出发，提出将磁力矩器及姿态控制喷气发动机为执行部件设计卫星的姿态机动，以KBR系统、GPS接收机、星敏感器和磁强计为测量敏感元件的估计算法。该算法将KBR系统相位中心在轨标定问题转换为对卫星姿态四元数的求解，并采用Batch估计算法进行尝试性的仿真研究。不过，这种算法是建立在卫星动力学特性精确已知的基础上，而动力学模型在实际工程中不可能保证精确，存在着不确定性的误差，在这种情况下采用Batch估计算法很难保证标定精度。文献［4］提出估计状态的预测滤波法。在预测滤波法中，模型误差无需已知，而是作为解的一部分被估计，有效地解决了存在显著模型误差情况下的非线性问题；但是，该算法对初始状态信息的依赖程度很高，当初始状态信息存在较大误差时，其估计精度明显下降，甚至发散。

综合上述算法的特点，本文提出了一种利用预测卡尔曼滤波算法估计卫星的姿态四元数，以扩展卡尔曼滤波算法实现KBR 系统相位中心在轨标定的算法。当存在较大的卫星姿态动力学模型误差时，该算法仍能精确地实现KBR 系统相位中心的标定。同时，该算法采用三维偏差四元数代替四元数作为状态变量，避免了估计过程中四元数单位约束性被破坏。

2 KBR 系统相位中心在轨标定算法

KBR 系统相位中心在轨标定算法的基本过程（见图1）为：首先，利用姿态控制器发送指令给磁力矩器及姿态控制喷气发动机，使卫星按照设计的姿态机动规律进行姿态机动；然后，将星敏感器数据代入预测卡尔曼滤波算法中，估计出卫星的姿态四元数；最后，利用扩展卡尔曼滤波算法实现KBR 系统天线相位中心的在轨标定。

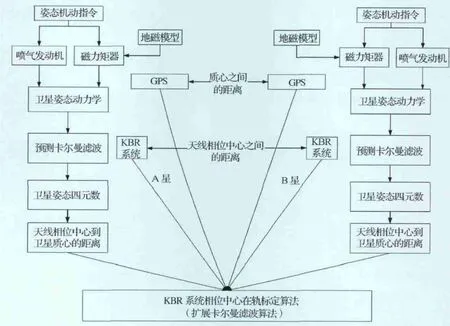
图1 数值仿真算法Fig.1 Numerical simulation algorithm

2.1 卫星姿态机动规律

设重力测量卫星为A 星和B 星，则A 星俯仰／偏航机动规律为［3］

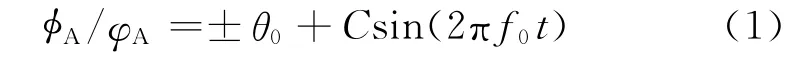
B星俯仰／偏航机动规律为

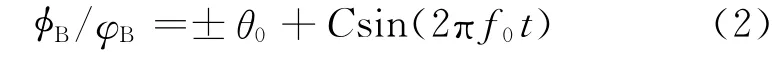
式中：φA和φB分别为A 星和B 星的俯仰角；φA和φB分别为A 星和B星的偏航角；C和f0分别为机动的振幅和频率；t为机动时间；θ0为初始偏置角。

卫星进行姿态机动，当θ0为正值时，定义为卫星正像机动；当θ0为负值时，定义为卫星镜像机动。A 星的姿态机动过程为：首先进行卫星俯仰机动，卫星的其他方向变化都须保持原标称姿态；俯仰机动结束后，卫星调整为三轴稳定状态，再进行偏航机动；在A 星机动过程中，B 星的姿态始终保持原标称姿态。B 星的姿态机动过程同A 星一致。在相位中心在轨标定算法中，只取机动过程中的数据进行标定。

2.2 KBR系统模型

KBR系统输出的双星距离Robs的表达式为［5］

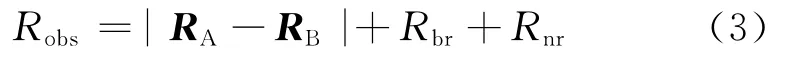
式中：RA和RB分别为A 星和B 星的相位中心在J2000惯性坐标系下的位置矢量，见式（4）和式（5）；Rbr为KBR 系统 的零偏 误差；Rnr为KBR 系统的测量噪声误差。

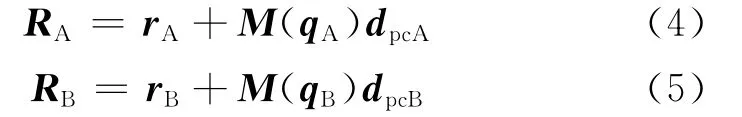
式中：rA和rB分别为A 星和B 星的质心在J2000惯性坐标系下的位置向量；dpcA和dpcB分别为A 星和B星的相位中心在卫星本体坐标系下的位置矢量；qA和qB分别为A 星和B 星的姿态四元数；M为卫星本体坐标系转换到地心惯性坐标系的转换矩阵，其表达式为

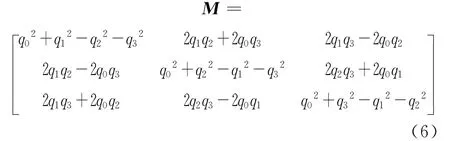
式中：q0，q1，q2，q3为卫星姿态四元数。

显然，在构建上述系统模型时，要利用到卫星姿态四元数q的信息，其计算公式为

角动量H＝Jpω，Jp为卫星的转动惯量矩阵；T为作用于卫星上的总力矩。

卫星运行期间，其转动惯量矩阵Jp存在不确定性，而且，作用在卫星上的总外部力矩受外部干扰力矩和其他摄动因素的影响，往往无法精确已知［6-7］。如果直接利用卫星姿态动力学方程式（7）计算卫星的四元数信息，其估计结果未必可靠，这是KBR 系统在轨标定的一个难点所在。本文引入预测卡尔曼滤波算法来解决这一问题，首先利用预测滤波算法估计外部力矩误差，然后利用卡尔曼滤波算法对卫星姿态进行估计，获得高精度的坐标系转换矩阵M，最后利用扩展卡尔曼滤波算法获得KBR 系统相位中心的估计值。

2.3 应用预测卡尔曼滤波算法的姿态四元数估计

设状态变量为X1＝［qH］T，在式（7）中增加力矩模型误差d（tk），得到姿态估计的状态方程为

式中：ωk，qk，Tk，Hk分别为卫星在tk时刻的角速度、姿态四元数、力矩和角动量，k为时间序号；I为单位阵；f（X1）为系统状态模型函数；G为模型误差分布矩阵。

姿态估计的观测方程为

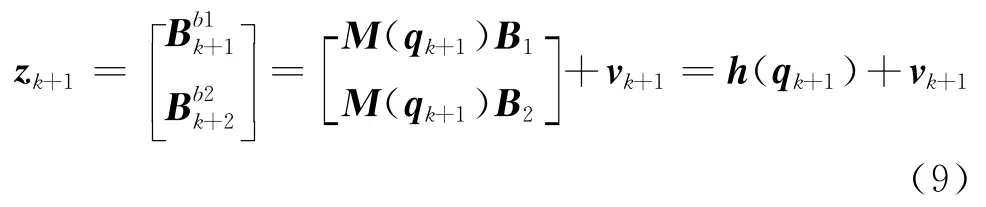
式中：和为tk＋1时刻的2个测量矢量；B1和B2为2个不平行参考矢量；h为系统观测模型函数；vk＋1为观测噪声。

将观测方程式（9）泰勒级数展开得［4］

式中：Δt为采样时间间隔。

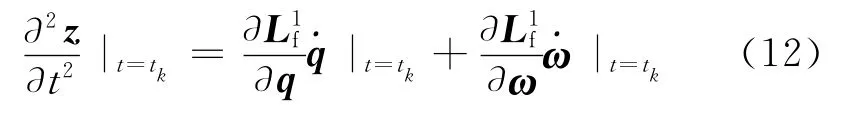
式中：为f（X1）的一阶李导数；f（X1）的二阶李导数

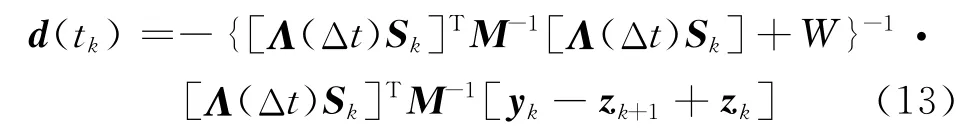
式中：W为3×3阶加权矩阵；M为测量噪声协方差矩阵。

将状态方程式（8）离散化，保留二阶项，可得到离散的状态估计传播方程如下。

式中：A［X1（tk）］＝

将tk＋1时刻星敏感器输出测量值，tk时刻估计值代入式（13），求得模型误差d（tk）；然后把d（tk）代入式（14）中，计算出tk＋1时刻的一步状态估计值X1（tk＋1｜tk）。

为防止四元数的正交性奇异问题，对四元数误差进行降阶处理。设四元数误差为矢部误差，δq3为标部误差。给定姿态初始状态估计值及初始估计均方差误差P1（t0），利用扩展卡尔曼滤波算法［8］就可以得到卫星姿态四元数的估计值。其中，扩展卡尔曼滤波算法中的姿态状态转移矩阵为

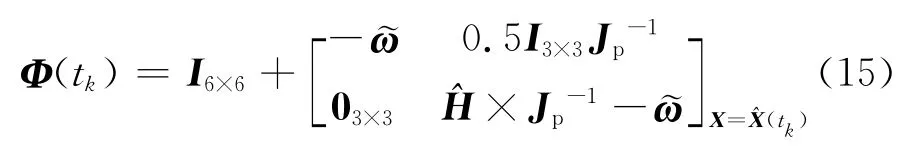
量测转移矩阵为

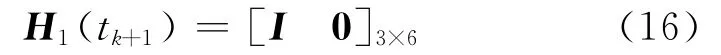
则矢部误差估计为

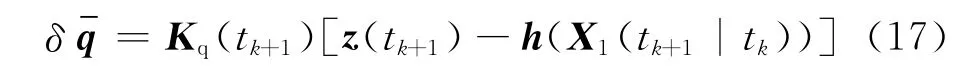
式中：Kq（tk＋1）为姿态反馈增益矩阵。

标部误差估计为

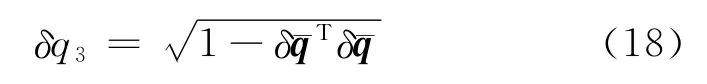
姿态四元数的估计值为

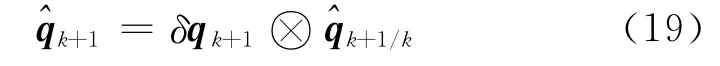
2.4 应用扩展卡尔曼滤波算法的KBR 系统相位中心在轨标定

获得卫星姿态四元数的估计值后，便可精确计算两颗卫星的坐标转换矩阵M，在此基础上，设状态变量X2＝［dpcAdpcB］T，建立式（20）中的状态方程和观测方程，利用扩展卡尔曼滤波算法递推公式［8］即可估计出KBR 系统相位中心的偏差值。

式中：传递函数矩阵H2（t）＝［eTM1-eTM2］，e＝

3 数值仿真

设A 星和B星均运行在高度为450km、偏心率为0.001、倾角为89.9°的轨道上，两星相距239km，它们的初始轨道和姿态参数如表1所示。

表1 双星初始参数Table 1 Initial parameters of two satellites

仿真中采用的卫星摄动模型如表2所示，仿真中卫星的测量误差参数如表3所示［9］。

表2 双星动力学模型Table 2 Dynamic model of two satellites

表3 双星测量误差Table 3 Measurement errors of two satellites

卫星姿态机动过程中的机动规律设置为φ／φ＝±2＋sin（2πt／250）；为了减小多径误差对KBR 系统测距误差的影响，卫星每种姿态机动时间取机动周期的整数倍，这里取1000s。为了分析得到数据采集的轨道相位与相位中心标定误差的关系，分别选在赤道附近、北极附近进行卫星KBR 系统相位中心在轨标定。

定义重力测量卫星的本体坐标系为OXYZ，原点O位于卫星质心，X轴指向KBR 系统的相位中心，Z轴指向地心，Y轴与Z轴、X轴构成右手直角坐标系，则在卫星本体坐标系下赤道上空力矩模型估计误差曲线如图2所示。

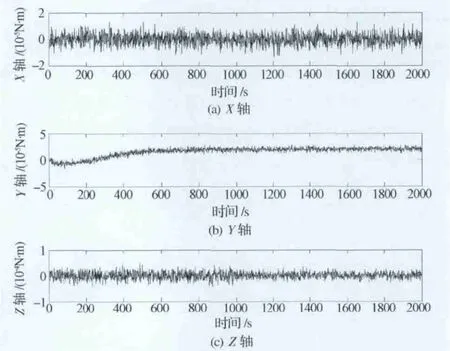
图2 力矩模型误差估计曲线Fig.2 Torques model estimation errors

对图2中的估值序列进行统计平均，得到力学模型误差的稳态估值为［0.96 18.8 0.97］×10-6N·m。标定过程中，KBR系统输出的距离观测值见图3，双星距离大概变化560m。标定过程中，卫星质心与KBR系统相位中心之间的距离变化见图4，其距离变化周期与姿态角机动周期相同，为250s，变化幅值为1.6mm。KBR系统的多径传播误差见图5，机动过程中多径传播误差最大为1.45mm，变化周期为250s。北极附近的分析结果与赤道上空的一致。

在赤道上空，当初始状态估计出现很大的误差，X1（t0）＝［0.5 -0.5 0.5 0.5］T时，姿态估计结果见图6和图7。

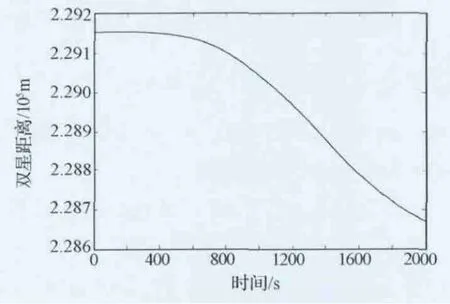
图3 KBR 系统距离观测值Fig.3 KBR system range observation

图4 卫星质心与KBR 系统相位中心之间的距离变化Fig.4 Distance changing between satellite centers of mass and KBR system phase centers

图5 KBR 系统相位中心标定过程中多径传播误差值Fig.5 Mutipath error during KBR system phase center calibration

图6 俯仰机动姿态估计误差Fig.6 Attitude estimation errors at pitch maneuver

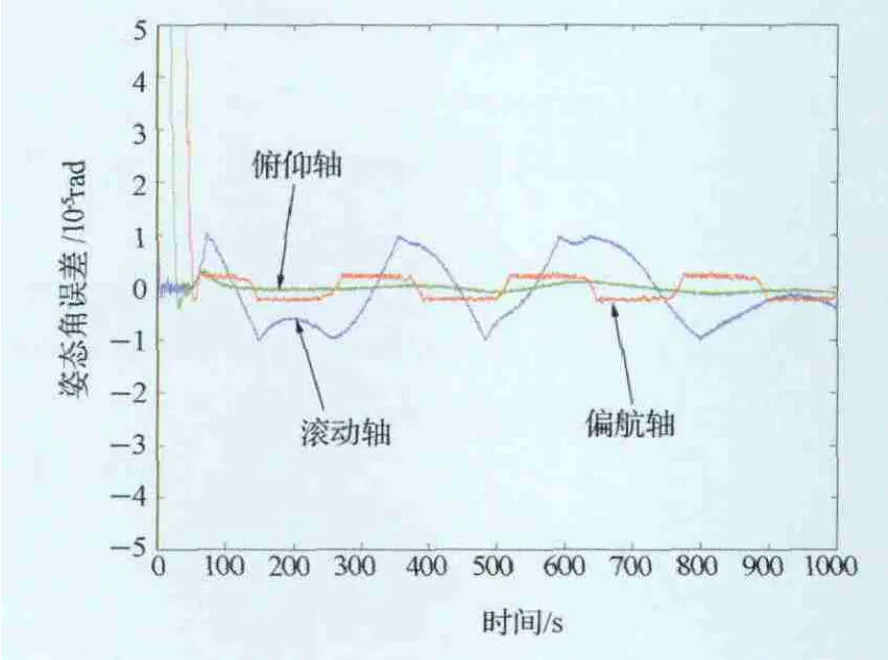
图7 偏航机动姿态估计误差Fig.7 Attitude estimation errors at yaw maneuver

单独使用卡尔曼滤波算法的估计值并不能收敛于真值，估计结果严重发散。预测卡尔曼滤波算法可以实现姿态四元数的准确估计，三轴估计误差均在20μrad以内。这是由于预测卡尔曼滤波算法采用更新量测矩阵信息，保证了模型误差估计值的准确性，因而其鲁棒性更强。需要指出的是，预测卡尔曼滤波算法的上述性能是以牺牲运算量为代价的，其运算量为4430次乘法和2986次加法，约是预测滤波算法的3倍，但是要小于通常采用的卡尔曼滤波算法。

设相位中心估计值为dePCi，它与理论值dPCi之间的夹角θier作为标定误差。根据文献［10］，如果要将由KBR 系统相位中心偏移引起的测距误差控制到1μm，则标定误差θier必须在0.3mrad以内。分别采用文献［3］中的Batch估计算法及本文提出的算法，在相同的输入条件下得到相位中心的标定结果，如表4所示。当初始状态估计出现很大的误差时，使用Batch估计算法结果无法收敛，而采用本文提出的算法，可以达到很好的估计结果。从标定结果可以看出，无论在赤道地区还是在北极地区，单独进行正像俯仰／偏航机动或者镜像俯仰／偏航机动，相位中心的标定结果均不能满足0.3mrad的精度要求，必须分别进行正像／镜像机动，然后将数据进行联合处理，才可达到精度要求。其主要原因是：单独进行正像机动或镜像机动，受多径传播误差影响较大；而将正像机动与镜像机动数据相结合，可有效抵消多径传播误差影响，使相位中心估计精度大幅度提高。总体而言，在该算法中，标定轨道相位的选取，对最终标定误差的影响并不是特别显著，赤道地区略优。从激励时长看，单次机动1000s的总机动时间是可以接受的，激励时间再长，喷气发动机燃料消耗较大，不利于卫星的长寿命运行。

表4 KBR 系统相位中心在轨标定误差Table 4 KBR system phase center in-orbit calibration errors mrad

4 结束语

KBR 系统相位中心在轨标定的一个关键问题，是如何高精度地获取卫星在轨机动时的姿态转换矩阵。针对这一问题，本文提出了一种应用预测卡尔曼滤波算法和扩展卡尔曼滤波算法的KBR 系统相位中心在轨标定算法，使KBR 系统相位中心标定误差优于0.3mrad。仿真结果表明：该算法鲁棒性强，对初始姿态误差不敏感，能有效利用预测卡尔曼滤波算法的优点。目前，滤波器的设计还有些复杂，在实际工程应用还要结合KBR 系统的具体工作特性进行深入研究，进一步优化滤波器结构，为重力测量卫星的工程化设计服务。

（References）

［1］佘世刚，王锴，周毅，等.高精度星间微波测距技术［J］.宇航学报，2006，27（3）：403-406 She Shigang，Wang Kai，Zhou Yi，et al.The technology of high accuracy inter-satellite microwave ranging［J］.Journal of Astronautics，2006，27（3）：403-406（in Chinese）

［2］Romans L.Optimal determination quaternion from multiple star camera sensors［R］.Pasadena，California：NASA JPL，2003

［3］Wang Furun.Antenna phase center determination of inter-communicating satellites［C］／／Proceedings of the AAS／AIAA Astrodynamics Conference. Washington D.C.：AIAA，2002：212-218

［4］John L.Predictive filtering for attitude estimation without rate sensors［J］.Journal of Guidance，Control and Dynamic，1997，15（3）：522-527

［5］张红军，赵艳彬，孙克新.星间微波测距系统相位中心在轨标定研究［J］.上海航天，2010，27（4）：1-5 Zhang Hongjun，Zhao Yanbin，Sun Kexin.Study on phase centers calibration of K-band ranging system during in-flight phase［J］.Aerospace Shanghai，2010，27（4）：1-5（in Chinese）

［6］Hall C D，Tsiotras P，Shen H.Tracking rigid body motion using thrusters and momentum wheels［J］.The Journal of the Astronautical Sciences，2002，50（3）：311-323

［7］Bang H，Choi H D.Attitude control of a bias momentum satellite using momentum of inertia ［J］.IEEE Transactions on Aerospace and Electronic System，2002，38（1）：243-250

［8］王本利，廖鹤，韩毅.基于MME／EKF 算法的卫星质心在轨标定［J］.宇航学报，2010，31（9）：2150-2156 Wang Benli，Liao He，Han Yi.On-orbit calibration of satellite center of mass based on MME／EKF algorithm［J］.Journal of Astronautics，2010，31（9）：2150-2156（in Chinese）

［9］Kim J R.Simulaton study of a low-low satellite-to-satellite tracking mission［D］.Austin：University of Texas at Austin，2000

［10］Wang Furun.Study on center of mass calibration and K-band ranging system calibration of the GRACE mission［D］.Austin：University of Texas at Austin，2003