梓木蒸汽爆破过程传热数值模拟初探
2014-12-27郝晓峰刘文金李贤军吕建雄孙德林陈新义
郝晓峰,刘文金,李贤军,吕建雄,孙德林,陈新义
(1.中南林业科技大学,湖南 长沙 410004;2.中国林业科学研究院木材工业研究所,北京 100091)
梓木蒸汽爆破过程传热数值模拟初探
郝晓峰1,刘文金1,李贤军1,吕建雄2,孙德林1,陈新义1
(1.中南林业科技大学,湖南 长沙 410004;2.中国林业科学研究院木材工业研究所,北京 100091)
针对梓木蒸汽爆破过程中传热机理的数值模拟进行研究。考虑木材内部水分、湿空气与固相骨架物质的对传热的影响,基于傅里叶导热定律,建立一维梓木爆破过程中传热数学模型,利用有限差分数学思想结合Fortran语言编写该模型数值计算程序,并通过实验验证了模型的准确性。结果表明该模型可以较为准确的反应梓木蒸汽爆破过程中的加热过程,能够定量分析板材内的温度、压力随时间变化的规律。
梓木;蒸汽爆破;传热机理;数值模拟
梓木Catalpa ovata G.Don.是非常用树种,分布在湖南、湖北等地,每年可提供3×106m3木材。梓木纹理美观、色质圆润,具有珍贵木材的纹理与色泽,但梓木材质松软,强度低,握钉力差,导致长期以来只能作为劣质材使用,产品附加值低。因此,通过木材改性提高梓木密度及强度,实现梓木高附加值利用具有重要的经济效益。近年来,国内外木材科技工作者发现蒸汽爆破预处理技术可以提高木材的渗透性。 金 川 靖、Kanagawa、Hayashi、Lee、Cai等研究发现通过低压蒸汽爆破预处理木材,可以提高木材的渗透性及干燥速率[1-7]。张耀丽、苗平等研究发现随着木材的径、弦向的渗透性均随着爆破温度、压力的增加而增加,同时发现蒸汽爆破预处理过的木材其内部管胞纹孔边缘开裂、射线薄壁细胞产生细小的裂隙以及导管内的侵填体剥落等现象[8-9]。夏金尉等研究了5种蒸汽爆破预处理工艺对落叶松木材细胞通道开启率的影响,并得出了5种蒸汽爆破预处理工艺中最优工艺[10]。
通过以上研究不难发现,蒸汽爆破预处理木材过程中,温度与压力的起着决定性作用,而温度又决定压力,因此,定量分析蒸汽爆破预处理过程中木材温度分布尤为关键。此外,蒸汽爆破预处理时间的长短也决定着能源的消耗,而关于蒸汽爆破预处理时间方面的研究也较少。因此,本研究的主要目的是针对蒸汽爆破预处理木材过程中传热过程的数学模型研究,定量分析蒸汽爆破过程中温度与压力随时间分布的变化规律。
1 木材蒸汽爆破预处理的物理与数学模型
1.1 物理模型
为定量分析蒸汽爆破预处理木材的传热规律,需对木材蒸汽爆破预处理过程中传热的物理现象进行简化,引入以下假设构建传热的物理模型。
假设1:木材视为多孔材料,由固相(细胞壁物质)、液相(自由水与吸着水)与气相(湿空气)组成,液相与气相存在于木材内部孔隙内(孔隙率为 ),三相连续均匀分布;
假设2:利用傅里叶传热定律表征木材在处理罐内加热过程,在加热过程中,木材内部固相的温度、液相温度与气相温度始终相同,内部没有热源产生;
假设3:在计算热物性参数时,将固相细胞壁、液相水与水蒸气视为并联网络,木材径向、弦向、纵向上的等效导热系数相同;
假设4:木材在处理罐内加热时,液相水与气相水蒸气始终保持相平衡,水蒸气对应相应温度下的饱和蒸汽压,小于外界罐体内水蒸汽的饱和蒸汽压,没有水分的移动,即忽略传质过程;
假设5:处理罐内的饱和蒸汽以对流方式加热木材,即对流传热边界为第三类边界条件。处理罐内木材试件厚度小于宽度和长度,传热主要沿厚度方向进行;
假设6:处理罐足够大,用于加热木材的热量消耗不会影响整个罐内的温度,即环境温度恒定。
1.2 数学模型
基于以上物理模型,建立梓木蒸汽爆破过程中传热的数学模型。首先,根据能量守恒定律,分别建立固相、液相与气相各自的能量守恒方程。
1.2.1 固相能量的控制方程

式(1)中物理含义为木材单位体积内固相骨架物质能量在单位时间内的增加量等于以导热的方式在单位时间内从单位体积边界传入的能量加上单位时间内单位体积木材液相水与湿空气传给固相骨架物质的能量。
1.2.2 液相水能量的控制方程

式(2)中物理含义为木材单位体积内液相水的能量在单位时间内的增加量等于以导热的方式在单位时间内从单位体积边界传入的能量加上单位时间内单位体积木材固相骨架物质与湿空气传给液相水的能量。
1.2.3 湿空气能量的控制方程
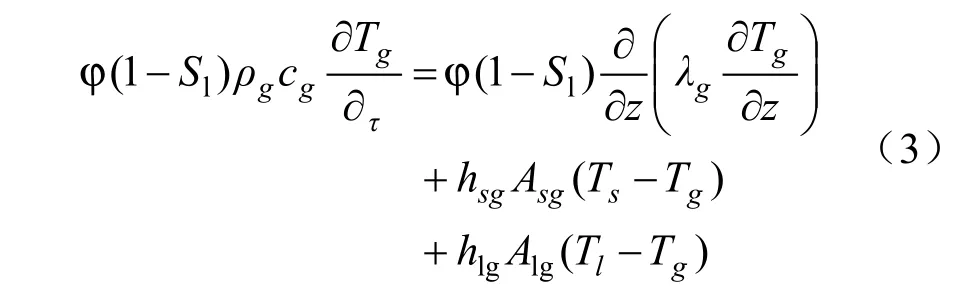
式(3)中物理含义为木材单位体积内湿空气的能量在单位时间内的增加量等于以导热的方式在单位时间内从单位体积边界传入的能量加上单位时间内单位体积木材固相骨架物质与液相水传给湿空气的能量。
在上述各式中,ρ为密度,单位为kg/m3;c为比热容,单位为J/(kg·K);T为温度,单位℃;τ为时间,单位为s;h为导热系数,单位W/(m2·K);A为各相之间接触面积,单位m2;下标s、l和g分别代表木材固相骨架物质、液相水和湿空气;
由假设2可知,

由假设3可知,推导过程详见参考文献[11]。
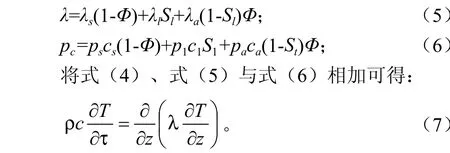
式(7)物理含义为木材单位体积内湿木材的能量在单位时间内的增加量等于以导热的方式在单位时间内从单位体积边界传入的能量。
1.2.4 边界条件与初始条件
从数学上讲,式(7)是二阶偏微分方程,应有初始条件与边界条件,从而构成偏微分方程定解问题。由假设5、假设6可知,边界条件如下:
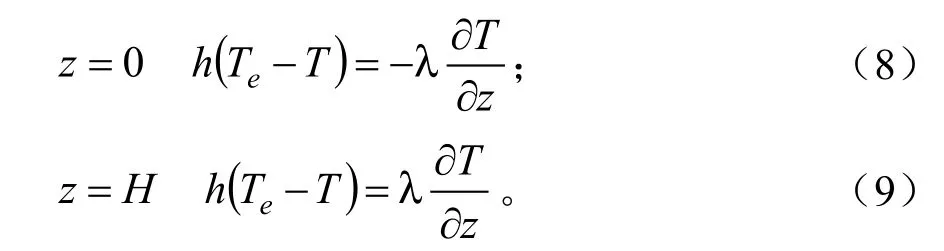
初始条件:

2 木材蒸汽爆破预处理数学模型的数值解
2.1 求解区域离散化
在建立差分方程之前,先将求解区域离散化。由假设5可知,本问题为一维非稳态木材加热问题,求解域是z坐标上长度为H的线段,即[0,H],这里z=0对应于木材的下表面,求解区域离散化就是把连续的线段[0,H]从z=0到z=H进行离散化处理。如图1所示,将区域[0,H]离散成JZ个节点,节点间有JZ-1个间距。连续自变量z离散成间距相同的有限个节点zj,下标j表示空间位置的次序,即z1,z2,…,zJZ。两邻近点的距离为Δz,称为空间步长,即Δz-H/(JZ-1)。

图1 空间连续区域内离散节点与步长Fig.1 The discrete notes and step size of space continuous area
与空间连续区域离散化相仿,时间区域也需要离散化,即将连续的时间域[0,τmax]内的自变量τ变成一系列离散的时刻τn,用上标n表示时间在不同时刻,n=1,2,…。两个离散时刻之间的时间间隔为Δτ,称为时间步长,如图2所示。
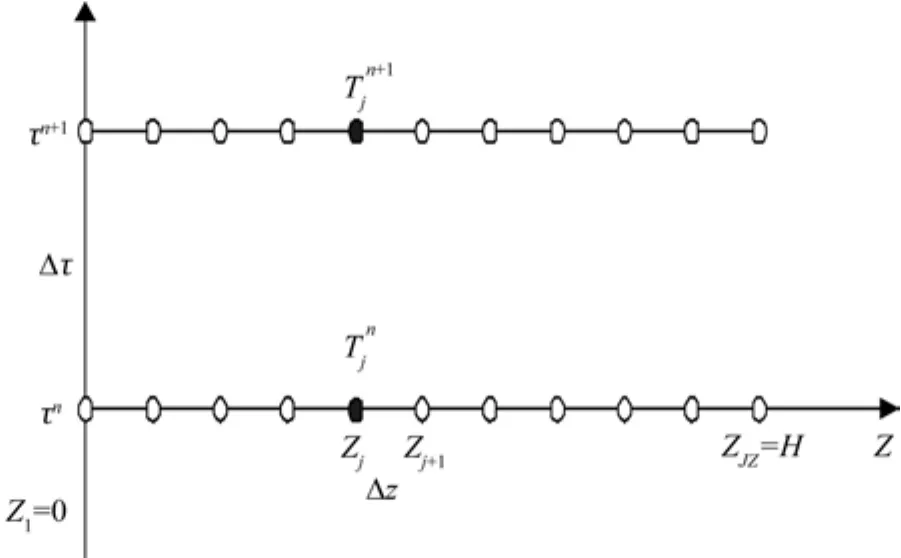
图2 空间与时间连续区域内离散节点与步长Fig.2 The discrete notes and step size of space and time continuous area
2.2 控制方程的差分形式
根据式(7)、式(8)和式(9)分别写出内单元与边界单元的差分控制方程。
2.2.1 内单元
根据控制方程式(7),内单元写成差分格式为

2.2.2 边界单元

这里需要指出的是,通过式(11)、式(12)、式(13)可知,本研究考虑导热系数及比热容随温度而发生变化。结合上述各单元的差分格式,利用Fortran语言,编写计算程序,此处略去程序。
3 材料与方法
从湖南常德市荣星家具公司购入梓木板材,密封后运回长沙。试件的尺寸为长度L=600 mm,宽度W=120 mm,厚度H=33 mm,初含水率为100%左右,实验设备为自制蒸汽压力罐及温度在线检测系统。将试件置于蒸汽罐内密封,通入饱和蒸汽加压加热木材,环境温度在150 ℃左右,加热木材46 min,并实时记录木材内部温度变化,如图3所示。

图3 试件加热示意Fig.3 The sketch map of specimen heating
4 结果与讨论
从图4可知,木材在升温过程中,芯层到表层存在温度梯度。2.88 mm处靠近表层(3.3 mm)升温速度较快,而1.65 mm芯层处,升温速度略慢于表层。每层之间的温度梯度相差不是很大,原因是木材初含水率较高,而水分的导热系数是空气的23倍以上,木材孔隙中大部分孔隙被水分占据,致使木材的导热系数增大。但图中1.65 mm处后期温度升温较快,原因可能是由于密封热电偶的胶水失效,导致该处与压力罐环境相通,属于实验误差。
将实验参数代入计算程序,即初始温度为T0为24 ℃,板厚为33 mm,罐内环境温度为150 ℃,模拟加热时间为50 min,数值模拟温度、压力分布如图5与图6所示。模型数值模拟的各层温度值与实验测量值升温趋势基本相同。为了进一步对比,将各层实验测量值与数值模拟值分别进行对比,如图6~图10所示,除图9数值模拟值低于实验测量值外,其余各处数值模拟值与实验测量值拟合较高。由图4~图5可知,板材加热30 min左右,其芯层温度可达到100 ℃,水蒸气饱和蒸汽压为0.1 MPa,远高于室温水蒸气分压0.002 MPa,此时泄压,即可实现蒸汽爆破效果。

图4 实验测量的温度分布Fig.4 The temperature distribution by experiment measurement
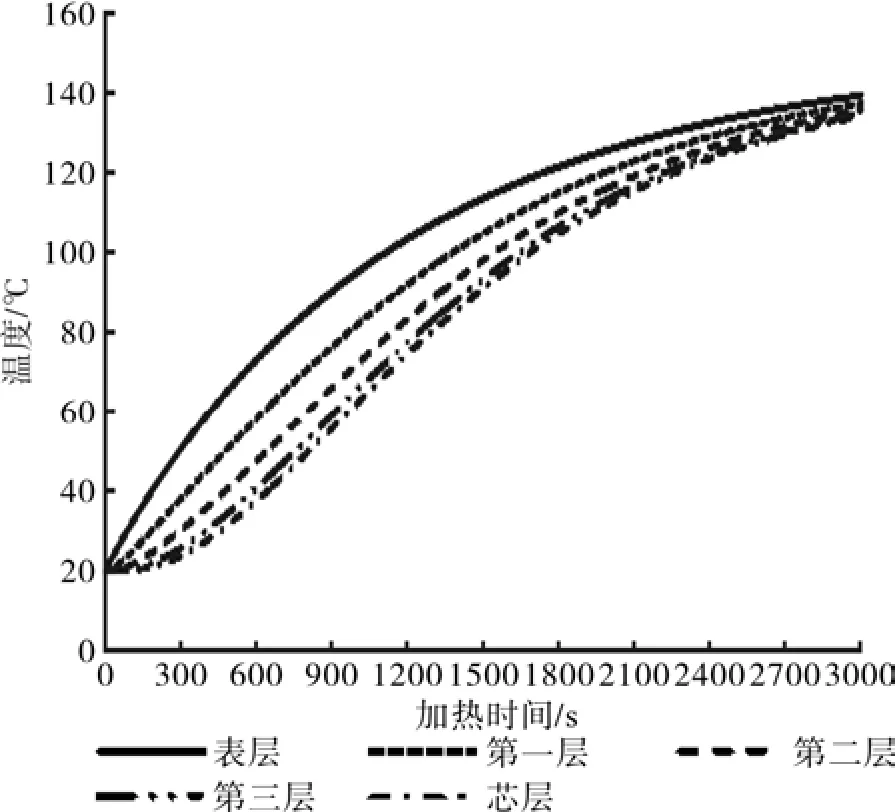
图5 数值模型模拟温度分布Fig.5 The temperature distribution by numerical calculation
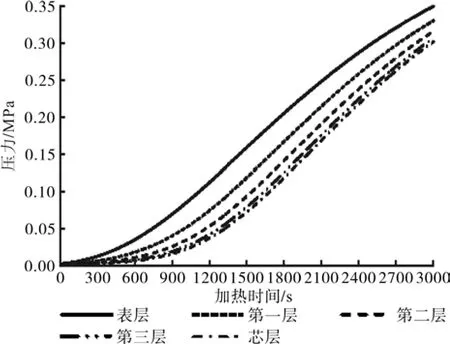
图6 数值模型模拟的压力分布Fig.6 The pressure distribution by numerical calculation

图7 2.88 mm处数值模拟温度值与实验测量温度值对比Fig.7 The comparison of predicted and experimental temperature at 2.88 mm
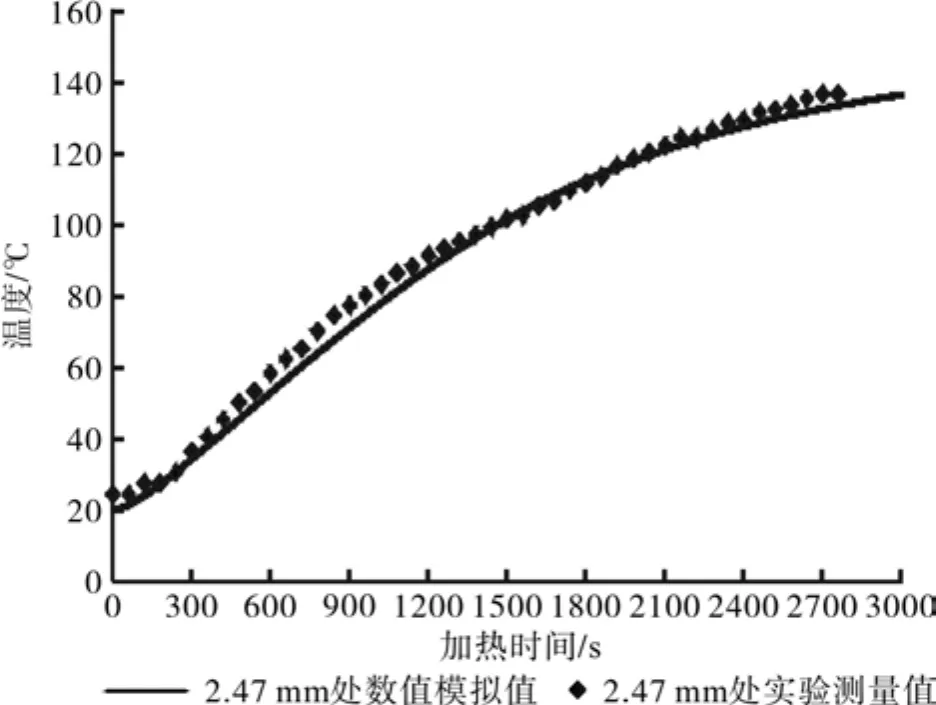
图8 2.47 mm处数值模拟温度值与实验测量温度值对比Fig.8 The comparison of predicted and experimental temperature at 2.47 mm
5 结 论
本研究基于傅里叶导热定律,建立一维的蒸汽爆破过程中传热模型,模型考虑了木材等效导热系数与等效比热容随温度变化对木材加热过程中的影响,基于有限差分数学思想并结合Fortran语言编写了该模型数值计算程序,并通过实验验证了模型的准确性,结果表明该一维数值模型可以较为准确的反应板材在蒸汽罐内的升温过程以及木材内水蒸气饱和蒸汽压分布,可用于计算板材在蒸汽爆破过程中加热时间。
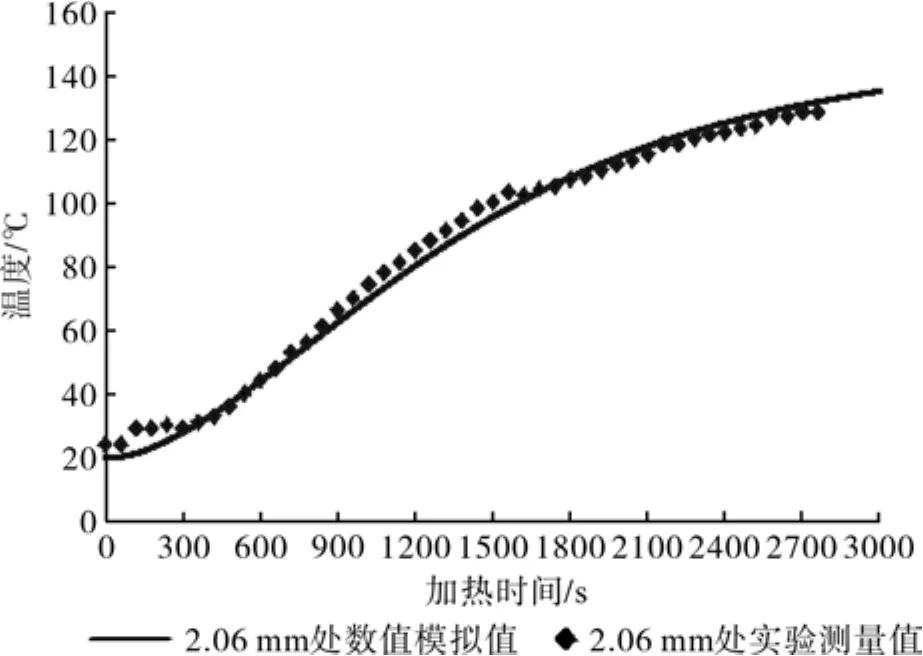
图9 2.06 mm处数值模拟温度值与实验测量温度值对比Fig.9 The comparison of predicted and experimental temperature at 2.06 mm

图10 1.65 mm处数值模拟温度值与实验测量温度值对比Fig.10 The comparison of predicted and experimental temperature at 1.65 mm
[1] 金川靖, 林和男, 涉谷昌资,等.局部水蒸爆法によるスキ材の乾燥性改善[J].木材工业 , 1992, 47(8):363 -366.
[2] Kanagawa Y, Hayashi K, Yasuzima M. Improvement of dryability by local steam explosion for Japanese cedar[C]Proceedings of 3rd IUFRO International Wood Drying Conference, Vienna,Austria. 1992: 269-276.
[3] Hayashi K K, Nakamura Y K. Improvement of dry ability and its distribution in aqua red timber by local steam explosion[C].Proceedings of the 4th International IUFRO Wood Drying Conference, Rotorua, New Zealand. 1994:359-365.
[4] Lee N H , Jung H S , Kang C W. Improvement of dryability of korean larch pillar in a RF/V dryer by low pressure steam explosion treatment [J ].Korean Furniture Society, 1998,9(2):55-63.
[5] Lee N H, Hayashi K. The effect of low pressure steam explosion treatment on the improvement of permeability in the softwood disks [J]. Journal of the Korean Wood Science and Technology,1997, 25(3):37-42.
[6] Lee N H, Nakamura Y K, et al. Improvement of dry ability of wood and its distribution by local steam explosion[J].Journal of the Society of Materials Science, 1995, 44:279-283.
[7] Cai L. Using steam explosion to improve the dryability of wet pocket wood[J]. Forest products journal, 2006, 56.
[8] 张耀丽,蔡力平,徐永吉.蒸汽爆破后毛果冷杉湿心材的渗透性分析[J]. 林业科学,2007,43(9):53-56.
[9] 苗 平, 庄寿增, 刘 彬,等. 蒸汽爆破预处理对柞木地板坯料干燥速率的影响[J].木材工业,2007,21(3):39-41.
[10] 夏金尉,张耀丽,蔡家斌. 蒸汽爆破开启落叶松木材细胞通道[J]. 福建农林大学学报:自然科学版,2013,42(5):543-547.
[11] 郝晓峰. 人工林杉木干燥过程传热传质数值模拟[D].北京:中国林业科学研究院,2013,73-75.
A preliminary study on numerical simulation of heat-transfer mechanism during Catalpa ovata wood steam explosion process
HAO Xiao-feng1, LIU Wen-jin1, LI Xian-jun1, LV Jian-xiong2, SUN de-lin1, CHEN Xin-yi1
(1. Central South University of Forestry and Technology, Changsha 410004, China;2. Research Institute of Wood Industry, CAF, Beijing 100091, China)
Numerical simulation of heat transfer mechanism during Catalpa ovata wood steam explosion pretreatment was studied by taking into account the effects of internal moisture, moist air and solid wood frame materials on heat transfer. One-dimensional heat transfer mathematical model was established based on Fourier law, the numerical calculation program for this model was compiled based on Finite Difference Scheme and Formula Translator Fortran, and the accuracy of this model was validated by the experiments. The results show that, this model can more accurately ref l ect the Catalpa ovate wood steam explosion process, and quantitively analyze the variation of temperature and pressure with time in tested wood.
Catalpa ovata G.Don.;steam explosion; heat-transfer mechanism; numerical simulation
S781.71
A
1673-923X(2014)12-0146-05
2014-04-04
林业公益性行业科研专项“梓木增重改良与实木家具制造关键技术研究”(201204712)
郝晓峰(1982-),黑龙江望奎人,讲师,博士,主要从事木材物理方向研究,E-mail: hxf8271@163.com
[本文编校:文凤鸣]
