试飞阶段可靠性评估方法及试验方案设计

高雅娟，陆 山

（1.中国飞行试验研究院，西安710089；2.西北工业大学动力与能源学院，西安710072）

试飞阶段可靠性评估方法及试验方案设计

高雅娟1，陆 山2

（1.中国飞行试验研究院，西安710089；2.西北工业大学动力与能源学院，西安710072）

提出将基于2参数威布尔分布的小子样零故障寿命试验方法用于航空发动机等高可靠性航空武器装备设计定型试飞阶段平均故障间隔时间评估以及可靠性专项试飞/地面试验设计，通过计算给出可靠性评估及试验设计系数用表；同时采用Matlab对航空发动机历史试验数据进行拟合，得到对应的形状参数；在此基础上，以某航空发动机为例对该方法工程应用的适用性和有效性进行验证。结果表明：该方法具有较强的工程应用性，可用于解决试飞阶段航空发动机等高可靠性产品可靠性评估及试验设计问题。

可靠性评估；航空发动机；小子样零故障寿命试验方法；威布尔分布；航空武器装备

0 引言

随着航空武器装备技术水平、可靠性研究与应用水平的提高，在设计定型/鉴定试飞或部队试用阶段，各方对可靠性评估工作越来越重视,将可靠性置于和性能同等重要的地位，对可靠性评估结论的准确性、评估方法的科学性、可靠性试验设计的合理性均提出了更高要求。在实践中，一方面由于高可靠性、长寿命产品研发和生产成本较高，其试验鉴定难度较大，试验周期和经费的矛盾也愈加突出。经典的试验分析与评估方法如极大似然法[1]以及单侧置信下限估计方法[2]受到了挑战[3]；而概率权重法、相关系数优化法、矩估计法[4]和灰色估计法[5]等新的理论也因为在工程中实际试验样本量小而具有一定的局限性。另一方面，如何合理设计可靠性专项试飞及地面试验，降低飞行试验费用，缩短飞行周期，是未来可靠性评估验证的发展趋势。因此开展小样本可靠性评估方法及试验设计具有重要的理论意义及巨大的经济价值，是当前以航空发动机为代表的高可靠性航空产品进行可靠性评估验证时需要关注的问题。目前对航空发动机等高可靠性产品小样本进行评估的方法主要有基于贝叶斯理论的小样本可靠性评估方法[6]、基于威布尔分布的无故障数据可靠性评估方法[7-9]、基于改进型Bootstrap方法的小子样试验评估方法[10]等。但这些方法较为复杂，且偏理论，在工程中应用较困难。

本文提出将美国《航空涡喷涡扇涡轴涡桨发动机通用规范》[11]中给出的当寿命分布符合2参数威布尔分布时构件可靠寿命零故障试验设计方法，推广应用于试飞期间航空发动机等高可靠性航空装备的可靠性评估及可靠性专项试验设计中。

1 小子样零故障寿命试验方法

设产品失效服从2参数威布尔分布[11]

式中：F为2参数威布尔分布的分布函数；η为特征寿命；β为形状参数；t为工作时间。

（t1，t2，L，tn）为 1 组随机试验件的故障时间样本，将其按从小到大的顺序排列，其最小次序统计量t(1)的分布函数可表示为

式中：Ft(1)

为t(1)的分布函数；n为试验样本数量。

将式（1）代入式（2）可得

令tγ为威布尔分布的最小次序统计量累积分布函数的下侧置信限，γ为相应的置信度，则最小次序统计量大于置信下限的风险为

由式（3）和式（4）得

这样，在已知形状参数β置信度γ样本数n和特征寿命η条件下，可得出每一试验件所需的试验时间。

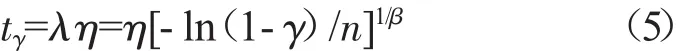
式中：λ为特征寿命乘子。

反之，已知形状参数β、置信度γ和特征寿命乘子 λ=tγ/η，也可求出所需的试验样本数

根据相关国军标要求，试飞阶段外场可靠性评估可取置信度γ=80%，此时的特征寿命乘子λ及样本数n的系数见表1、2。

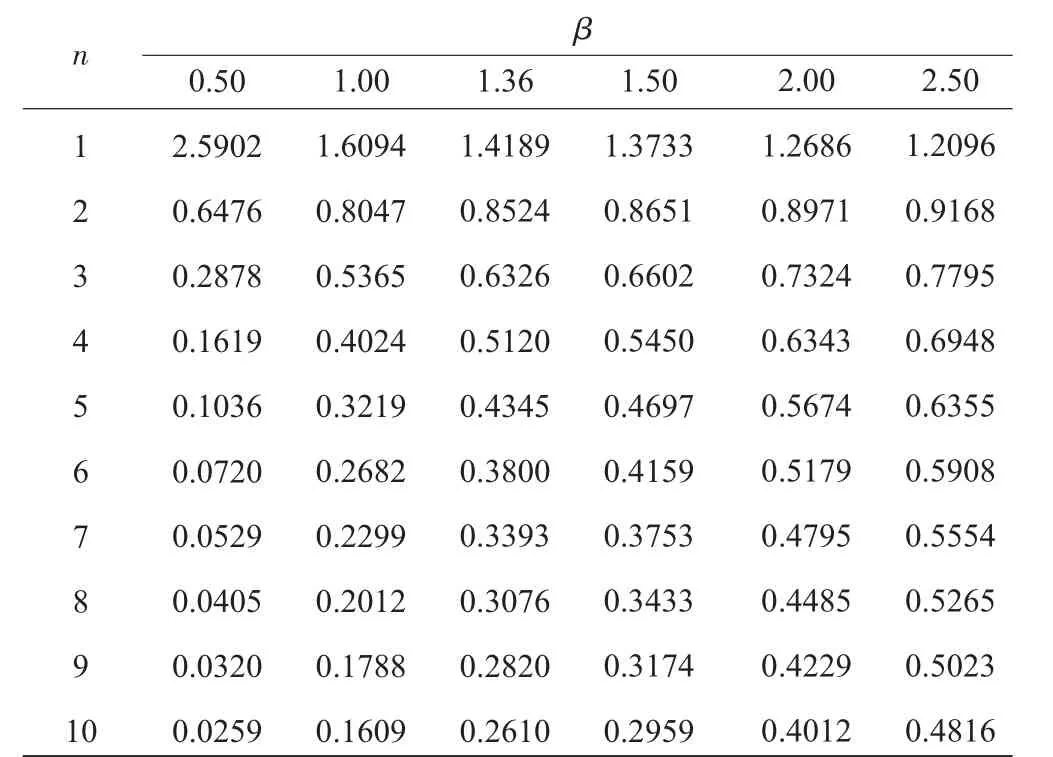
表1 零故障试验方案特征寿命乘子λ（γ=80%）

表2 零故障试验方案所需试件数n（γ=80%）

2 零故障寿命评估方法在高可靠性产品评估中的应用

可靠性评估验证工作是在综合考虑生产方和使用方的利益以及试验费用等诸多因素的基础上制定科学合理的试验方案，利用科学合理的数理统计学手段处理试验数据，来验证产品的可靠性指标是否满足要求。随着军方对可靠性评估工作的重视，可靠性理念已贯穿于军品的设计、生产、使用的各个阶段，积累了大量的可靠性试验数据，为航空装备设计定型/鉴定试飞期间可靠性综合评估提供了丰富的数据来源。在可靠性工程中，产品寿命分布类型可能是指数分布、正态分布、对数正态分布和威布尔分布等。由于威布尔分布含有3个参数，故其适应性较强，它可拟合浴盆曲线的3个阶段，因而在可靠性工程技术中应用广泛。

2.1 小子样零故障产品可靠性评估方法

采用小子样零故障试验方法进行航空发动机等可靠性评估的步骤如下：

（1）采用威布尔分布对已有设计、研制阶段的可靠性试验数据或相似产品的历史试飞数据进行拟合，确定各分布参数，从而确定该类产品寿命分布函数。由分布函数可得出任意给定可靠度时的寿命、给定寿命时的可靠度以及特征寿命值η；

（2）结合形状参数β和参试产品数量n，查表1得到特征寿命乘子λ；

（3）根据式（5）计算得到当航空发动机或零部件可靠寿命达到某一规定值时所需的试验时间t，与其试飞期间的实际工作时间T（可采用人工计时或在飞机或装备上安装相关的数据采集系统记录）相比较，若t≤T，则证明其可靠性已达到规定要求。

2.2 可靠性专项试验设计

随着军方对可靠性要求的提高，可靠性专项试飞或地面试验已成为航空发动机及武器装备设计定型/鉴定试飞的重要部分，能在真实的飞行环境条件下检验和评估产品的可靠性水平，为航空武器装备的定型/鉴定提供重要依据和参考。

由上节可知，利用小子样零故障寿命试验方法，能确定给定寿命可靠度和试件数时某一置信度水平下所需的试验时间，或给定寿命可靠度及试验时间时所需的试件数。根据本文提出的方法，合理进行设计定型/鉴定试飞期间飞行试验时间的设计，合理安排发动机数量以及试验时间：

（1）在参试产品数量确定的情况下，结合科研试飞任务采集、记录构件的工作时间，如果评估对象的工作时间不少于满足某一给定概率寿命时所需的试验时间，则产品的可靠性满足要求；若不能达到所需的试验时间要求，可根据理论计算结果，适当延长产品的试验时间。这样既可以避免试验时间不够，无法确定产品的可靠性是否满足要求，又可以降低试飞成本；

（2）在产品试飞周期（即产品的工作时间）确定的情况下，可以根据该理论确定满足某一概率寿命时所需的参试发动机数量，从而将寿命概率度量方法引入飞行试验中的可靠性评估工作中，提高评估精度，为航空发动机及装备的设计定型/鉴定提供可靠依据。

2.3 试飞阶段失效分布类型分析

在试飞阶段进行可靠性评估时，一般认为整机或电子类装备的早期故障已被排除，进入偶发故障阶段，因此采用基于指数分布的可靠性评估或试验设计；航空发动机的机械构件的失效则服从2参数威布尔分布[12]。

为进一步确定航空武器装备设计定型/鉴定试飞期间失效分布的类型，本文对航空电子设备以及航空发动机结构件的大量历史试飞数据进行分析，将产品的失效时间t和相应的累积失效概率F（t）利用Matlab 进行拟合[13]。

通过对全部19组航空设备（主要包括机载电子设备及机电类产品）的试飞数据分析表明，有15组数据服从指数分布，占全部数据的78.9%；有3组数据服从正态分布，占全部数据的15.8%；有1组数据服从对数正态分布，占全部数据的5.3%。指数分布的拟合结果如图1所示。

图1 指数分布拟合结果

采用Matlab对已有航空发动机机械类构件的试飞故障数据进行了拟合。拟合结果表明：在13组数据中，有11组服从2参数威布尔分布，占全部数据的84.6%，其形状参数的均值约为β=1.36。

因此，在采用基于2参数威布尔分布小子样零故障寿命试验方法对试飞阶段的航空发动机进行可靠性评估以及可靠性试验设计时，可取其形状参数β=1.36；而对航空电子产品进行可靠性评估以及可靠性试验设计时则可取β=1.0。

3 某型航空发动机可靠性评估及试验示例

平均故障间隔时间既是试飞阶段航空发动机基本可靠性评估参数,也是航空发动机可靠性评估优先选用的参数之一[14-15]。相关的国军标中给出了基于指数分布的点估计值评估方法，即平均故障间隔时间的点估计值等于产品的总工作时间除以总的故障数。因此，在采用2参数威布尔分布进行航空发动机的可靠性评估及试验设计时，可取平均故障间隔时间点估计值对应的可靠度为50%。

已知某航空发动机失效分布函数符合2参数威布尔分布，形状参数β=1.36，要求置信度γ=80%，平均故障间隔时间要求不小于150 h，参试产品为2台，则该航空发动机可靠度为

对应的特征寿命

选取2台参试产品，从表1可以查出特征寿命的乘子λ=0.8524。由此可得，该型发动机平均故障间隔时间达到指标要求所需的无故障工作时间T=0.8524×196=167 h。

因此，当2台该型航空发动机中最短工作时间超过167 h而未发生故障时，其平均故障间隔时间达到规定指标要求。

同样，若已知某航空发动机的失效服从威布尔分布，其形状参数β=1.36，置信度γ=80%，平均故障间隔时间要求不小于120 h，预计该型航空发动机的试验时间约为142 h，则对应的特征寿命

特征寿命乘子

由表2可知，此时所需的参试发动机为2台。

4 结论

（1）小子样零故障寿命试验方法可用于以航空发动机为代表的高可靠性航空武器装备在设计定型/鉴定试飞期间的可靠性定量评估及可靠性试验设计，将可靠性的概率度量引入对试飞期间平均故障间隔时间的评估，提高了评估精度，也为可靠性试验设计提供了新方法；

（2）形状参数β由以往产品的失效数据和分布形式确定，与产品的失效模式有关。随着可靠性试验水平逐步提高以及同类或相似产品的可靠性数据的不断丰富，有关威布尔分布的参数β以及η的取值精度会越来越高，其评估结果也会趋于精确，该方法的应用范围也会更广泛。

[1]金少华，李志刚，陆俭国,等.关于威布尔分布的1种参数估计方法[J].天津轻工业学院学报，2003，18（1）：43-45.JIN Shaohua，LIZhigang，LU Jianguo,etal.A parameter estimation method forWeibull distribution[J].Journal of Tianjin University of Light Industry，2003，18（1）：43-45.(in Chinese)

[2]李良巧.可靠性工程师手册 [M].北京：中国人民大学出版社，2012：241-242.LI Liangqiao.Handbook of certified reliability engineer[M].Beijing：China Renmin University Press，2012：241-242.(in Chinese)

[3]朱寿雷，彭绍雄，董蒙.Weibull分布下的系统可靠性评估方法研究 [J].电子产品可靠性与环境试验，2012，28（1）：20-23.ZHU Shoulei，PENG Shaoxiong，DONG Meng.Reliability evaluation ofmissile weapon systems with Weibull distribution[J].Electronic Product Reliability and Environment Testing，2012，28（1）：20-23.(in Chinese)

[4]严晓东，马翔，郑荣跃，等.三参数威布尔分布参数估计方法比较[J].宁波大学学报，2005，18（3）：301-305.YAN Xiaodong，MA Xiang，ZHENG Rongyue，et al.Comparison of the parameters estimation methods for 3 parameter Weibull distribution[J].Journal of Ningbo University，2005，18（3）：301-305.(in Chinese)

[5]郑荣跃，严剑松.威布尔分布参数估计新方法研究[J].机械强度，2002，24（4）：599-601.ZHENG Rongyue，YAN Jiansong.New estimation method of three parameterWeibull distribution[J].Journal of Mechanical Strength，2002，24（4）：599-601.(in Chinese)

[6]秦明，巫世晶，彭潇，等.1种服从威布尔分布装备的可靠性评估方法[J].武汉大学学报，2008，41（6）：100-102.QIN Ming，WU Shijing，PENG Xiao，et al.A reliability evaluationmethod for equipmentwith aWeibull failure distribution[J].Engineering Journal of Wuhan University，2008，41（6）：100-102.(in Chinese)

[7]陆祖建，张仕念，张国彬，等.威布尔分布无故障数据的可靠性评估[J].电子产品可靠性与环境试验，2011，29（6）：6-9.LU Zujian，ZHANG Shinian，ZHANG Guobin，et al.Reliability assessment for zero failure data in Weibull distribution[J].Electronic Product Reliability and Environment Testing，2011，29（6）：6-9.(in Chinese)

[8]赵宇，杨军，马小兵.可靠性数据分析教程[M].北京：北京航空航天大学出版社，2009：78-82.ZHAO Yu，YANG Jun，MA Xiaobing.Tutorial for reliability data analysis[M].Beijing：BeiHang University Press，2009：78-82.(in Chinese)

[9]陈家鼎.生存分析与可靠性 [M].北京：北京大学出版社，2005：126-130.CHEN Jiading.Survivability analysis and reliability[M].Beijing：Peking University Press，2005：126-130.(in Chinese)

[10]黄玮，冯蕴雯，吕震宙.基于Bootstrap方法的小子样试验评估方法研究[J].机械科学与技术，2006，25（1）：31-35.HUANG Wei，FENG Yunwen，LYU Zhenzhou.Study on small scale sample test estimation method based on bootstrap method [J].Mechanical Science and Technology，2006，25（1）：31-35.(in Chinese)

[11]陆山，吕鸿雁.小子样零构件可靠寿命零故障试验评估方法[J].机械强度，2006，28（3）：411-414.LU Shan，LYU Hongyan.Assessment method of reliability life by zero failure experiments of small sample components[J].Journal of Mechanical Strength，2006，28（3）：411-414.(in Chinese)

[12]赵宇.可靠性数据分析[M].北京：国防工业出版社，2011：34-35.ZHAO Yu.Data analysis of reliability[M].Beijing：National Defense Industry Press，2011：34-35.(in Chinese)

[13]贺国芳，许海宝.可靠性数据的收集与分析[M].北京：国防工业出版社，1995：39-41.HEGuofang，XU Haibao.Collection and analysis of reliability data [M].Beijing：National Defense Industry Press，1995：39-41.(in Chinese)

[14]谢静，范文正，谢镇波，等.某型军用发动机使用可靠性评估[J].航空发动机，2012，38（6）：43-47.XIE Jing，FAN Wenzheng，XIE Zhenbo，et al.Evalution of military engine service reliability[J].Aeroengine，2012，38（6）：43-47.(in Chinese)

[15]徐可君，江龙平.军用航空发动机可靠性和寿命管理[J].中国工程科学，2003，5（1）：82-88.XU Kejun，JIANG Longping.Reliability and life cyclemanagement of military aeroenging [J].Engineering Science，2003，5（1）：82-88.(in Chinese)

乌克兰AI-436T12发动机

AI-436T12发动机于2005年由乌克兰的伊夫琴科-前进设计局联合马达-西奇公司以及俄罗斯的礼炮公司、乌法发动机生产联合体、喀山发动机生产联合体等单位共同开始研制，礼炮公司为主生产单位。AI-436-T12发动机的研制预计花费45～60亿美元，主要依靠国家支持以及私企和国企的投资，计划在2015～2017年完成研制工作。

AI-436T12发动机是技术成熟的D-436T1发动机的深度改型，曾用代号D-436-TX，除了计划配装中短程干线客机MS-21外，还可用于配装俄印联合研制的多功能运输机（MTA）等飞机。

AI-436-T12发动机结构设计中采用了许多新技术方案，如带宽弦无凸肩叶片的风扇、齿轮传动减速器、新型压气机、新型燃烧室、带陶瓷涂层的涡轮叶片等，可以保证飞机具有高的燃油效率、合理的价格和低水平的噪声，污染物排放水平满足最严格的环保标准要求。

AI-436-T12发动机的性能参数：起飞状态推力为117.6 kN，耗油率为0.272 kg/daN·h，空气流量为557.3 kg/s，涵道比为10.25，增压比为26.33，燃气温度为 1568 K；最大巡航状态（H=11 km，Ma=0.8）推力为23.5 kN，耗油率为0.554 kg/daN·h；风扇直径为2070mm，净质量为2250 kg，发动机质推比为0.188 kg/daN。

（中航工业动力所 刘 静）

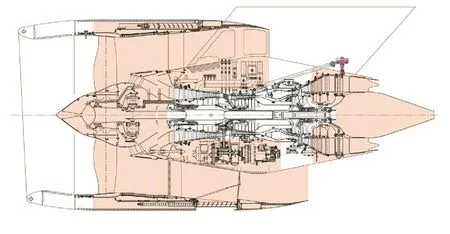
AI-436T12发动机结构

Reliability AssessmentMethod and Test Scheme Design During Flight Test

GAO Ya-juan1,LU Shan2
（1.Chinese Flight Test Establishment，Xi'an 710089,China； 2.Schoolof Power and Energy,Northwestern Polytechnical University,Xi'an 710072,China）

A zero-failure life testmethod for small sample component based on two-parameterWeibull distribution was proposed to solvemean time between failure assessment issues ofhigh reliability aeronautical products such as aeroengines,also to design the flight test and ground test scheme during qualification and type approval process.The coefficients used for reliability assessment and test scheme design were calculated and the tabulations were included.Then shape parameter was derived through curve fitting analysis of aeroengine historical flight test scheme data by Matlab.At last,the applicability and validity ofmethod was verified by reliability assessment and test scheme design of an aeroengine.The result shows that themethod could apply to solving reliability assessment and test scheme design for high reliability aeronautical products.

reliability assessment;aeroengine;zero-failure life testmethod for small sample component;Weibull distribution;aviation weapon equipment

V263.3

A

10.13477/j.cnki.aeroengine.2014.03.014

2014-01-26

高雅娟（1981），女，硕士，研究方向为航空发动机可靠性和维修性评估验证；E-mail：tigerwangjianfeng@163.com。

高雅娟，陆山.试飞阶段可靠性评估方法及试验方案设计[J].航空发动机，2014，40（3）：66-70.GAOYajuan，LUShan.Reliability assessment method and testscheme design duringflight test[J].Aeroengine，2014，40（3）：66-70.