选修4-2《矩阵与变换》与《高等代数》

田 莹

（沈阳师范大学，辽宁 沈阳110034）

1 选修4-2《矩阵与变换》中矩阵的引入

对于高中生它们对于矩阵没有接触过，是一个新的概念，非常的陌生。

其引入过程如下：设直线l在平面α内，那么对与平面α内任意一点p，都存在平面α内唯一一点p'，使p'与p关于直线l对称，我们称这样的对称关系为平面α关于直线l的反射变换。进一步，如果在平面α内建立直角坐标系xoy，那么平面内的点与有序实数对（x，y）之间就建立了一一对应。这样，我们又可以从代数的角度来研究反射变换，例如，关于x轴的反射变换，把平面α内的任意点p（x，y）变成它关于x轴的对称点，p'（x'，y'）,对于坐标p（x，y）与p'（x'，y'）可以得到：

显然，表达式①完全刻画了关于x轴的反射变换，因此，也称①为关于x轴的反射变换。

我们将反射变换①变形为：

由于②式由右端式子中x，y系数唯一确定，我们把它们按原来的顺序写出来，并在两端分别加上一个括号，就得到正方形数表,正方形数表也完全刻画了关于x轴的反射变换，我们把这种正方形数表称为二阶矩阵，这样关于x轴的反射变换就可以有二阶矩阵完全确定。事实上，在平面直角坐标系xoy内，很多儿何变换都具有下列形式：

其中系数a，b，c，d均为常数，我们把形如③的儿何变换叫做线性变换，③式叫做这个线性变换的坐标变换公式。我们引进正方形数表]，那么线性变换③可以由唯一确定。像这样，由4个数a，b，c，d排成的正方形数表]称为二阶矩阵。

2 《高等代数》中矩阵的引入

《高等代数》由多项式、行列式、线性方程组、矩阵、二次型、线性空间、λ-矩阵、欧几里得空间、双线性函数与辛空间十个章节组成，是中学代数的继续和提高，是大学数学专业的基础课之一。在其中线性方程和矩阵一直贯穿始终。对于大学生的学习是在第一章多项式的铺垫下，在第二章行列式中直接定义矩阵的符号。

对于二元线性方程组

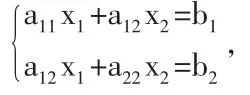
当a11a22-a12a21≠0时，次方程组有唯一解，即

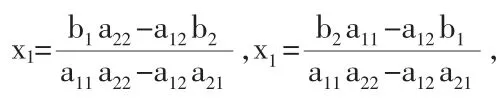
我们称a11a22-a12a21为二级行列式，用符号表示为：

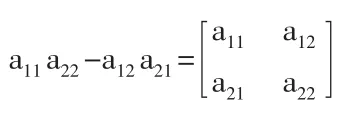
于是上述解可以用二级行列式叙述为：

当二级行列式

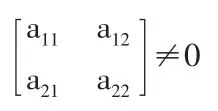
时，该方程组有唯一解，即

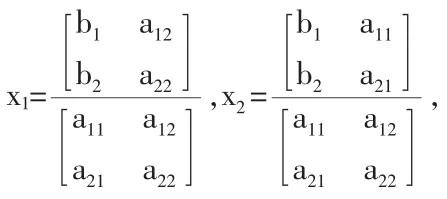
同理由三元线性方程组，定义了三级行列式。在其后，应用排列对矩阵的意义进一步对矩阵进行解释。

n级行列式

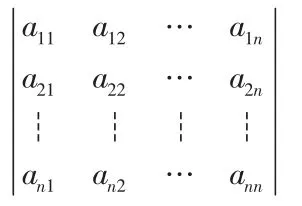
等于所有取自不同行不同列的n个元素的乘积

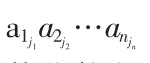
的代数和，这里j1，j2…jn是1,2，…，n的一个排列

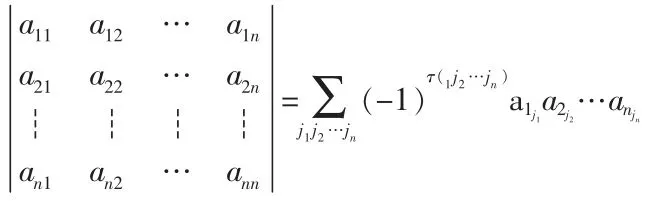
接着就是学习对行列式的变形与展开，线性方程组的一些重要性质反映在它的系数矩阵和增广矩阵的性质上，并且解方程组的过程也表现为变换这些矩阵的过程，除线性方程组之外，还有大量的各种各样的问题也都提出矩阵的概念，并且这些问题的研究常常反映为有关矩阵的某些方面的研究，甚至于有些性质完全不同的、表面上完全没有联系的问题，归结成矩阵问题以后却是相同的，这就使矩阵成为数学中一个极其重要的应用广泛的概念。

［1］刘绍学.矩阵与变换[M].人民教育出版社.

［2］王鄂芳,石生明.高等代数[M].3版.高等教育出版社.