基于黏弹性理论液相共烧结模型的建立及应用研究

黄华龙，李益民，潘文强

（中南大学粉末冶金国家重点实验室，长沙 410083）

自20世纪80年代以来，功能梯度材料（FGM）由于其成分或组织沿截面呈梯度连续变化，能够同时获得高硬度与高韧性，在切削工具、矿用工具和耐磨耐蚀零件等方面有着广泛的应用[1-5].但是大部分功能梯度材料在共烧结法制备过程中会出现液相，并可能产生两个方面的问题：第一，由于热膨胀系数的差异，在烧结过程中界面两端材料容易产生界面应力，促进或者抑制了共烧结合金的致密化[6-10]；第二，由于共烧结过程出现液相，界面两端毛细管力的差异引起液相的扩散迁移，容易影响到共烧结合金的密度梯度再分布[11-14]，由于两者的变化过程异常复杂，因而目前对于液相共烧结的作用机理也没有研究清楚.然而随着计算机模拟仿真技术的快速发展，许多学者通过建立合适参数的模型，对液相烧结、液相迁移和固相共烧结的作用机理进行了有益探索，其中J.Svoboda等[15-16]通过分析液相烧结机制得到一个液相烧结模型，Zhigang Zak Fang等[17]通过分析液相迁移动力学原理得到一个液相迁移模型，何浩等[9-10]基于黏弹性本构方程得到一个固相共烧结模型，但现有的这些理论模型不能较好地反映生产实践中液相共烧结的液相迁移以及致密化过程，因此开展液相共烧结模型的研究显得十分重要.

本文首先建立液相共烧结的物理模型和数学模型，研究界面应力和液相迁移对两侧液相共烧结材料烧结行为的作用机理，建立异种材料的液相共烧结模型.其次通过YG8硬质合金共烧结实验对模型进行验证.最后探讨了模型的关键问题和适用范围.

1 模型建立

本研究中的液相共烧结，主要是指由硬质耐火相基体材料 （如Si3N4、WC等）和黏结相添加物 （如Al2MgO4、Co等）构成的材料体系，采用粉末冶金方法制备共烧结压胚，在室温下逐渐升温，在远低于基体材料熔点温度下其黏结相会形成液相并发生迁移，从而使共烧结体快速达到全致密，因此可将液相共烧结分为3个阶段：固相共烧结阶段、部分液相共烧结阶段、完全液相共烧结阶段.

1.1 基本假设

一般在液相等温烧结开始之前，黏结相已经完全液化而且烧结体已高度致密化，如WC-Co系列合金Co相熔点在 1 367.718～1 375.086℃之间[18]，在等温烧结前其相对密度接近1（平均值为0.97）如图1所示[19].即在升温烧结出现液相的时候，烧结体致密化速率在很短时间内达到峰值，又升温速度较快时间较短，由此可认为在升温过程中形成的液相只是促进烧结体致密化而没有发生迁移.

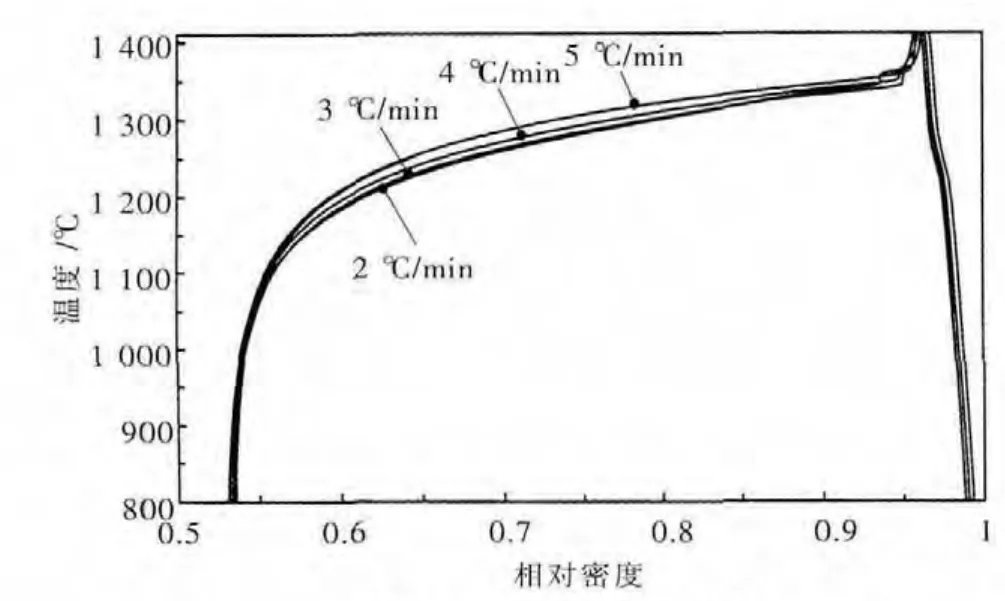
图1 WC-Co致密化曲线

同时根据液相迁移模型和固相共烧结模型的分析可知，界面应力和液相迁移压力产生的机理完全不同，因此可作以下合理假设：①在等温烧结之前，共烧结两端形成的液相主要是促进了致密化而没有发生迁移；②在等温烧结之后，两端的黏结相已经完全熔化并逐渐开始迁移；③在等温烧结之后，界面应力和液相迁移压力都是随着相应状态变量的变化而变化，两者没有必然联系.

1.2 物理模型

液相共烧结试样示意图如图2（a）所示，A和B分别为两侧不同材料，长度分别为L，x为距离界面处的距离，假设初始时刻B端较A端收缩较快，取共烧结界面A、B两侧无限靠近界面处的两微元进行分析，并根据基本假设可以得到液相共烧结3个阶段的物理模型：①在固相共烧结阶段，两端还没有形成液相，根据固相共烧结模型可知，该阶段只有界面应力在影响两端的致密化过程，其中界面应力△σ作用示意图如图2（b）所示；②在部分液相共烧结阶段，两端不一定会同步形成液相，既可能存在界面应力也可能存在液相迁移，难以定量分析两端液相迁移压力和致密化速率的变化，根据基本假设可知该阶段两端形成的液相主要是促进致密化而没有发生迁移，即可以假想界面处存在一堵墙如图2（c）所示，该阶段是界面应力在影响两端致密化过程；③在完全液相共烧结阶段，两端的黏结相已经完全变成液相，既存在界面应力也存在液相迁移，而且该阶段往往会发生在等温烧结之前，由于升温速度较快时间较短，可认为界面处的假想墙在等温烧结之后才撤掉，该阶段界面应力和液相迁移会同时影响两端密度梯度的分布.根据液相迁移模型可以假想界面处存在一个液池如图2（d）所示，两端液相迁移的方向是一致的，假设B端液相迁移压力大于A端的，那么液相会从A端迁移到B端，界面处液池会从A端吸入液体引起A端体积收缩，而B端会从液池吸入液体引起B端膨胀，又由液相烧结模型可知液相含量对固相颗粒烧结颈长大机制影响很小甚至可以忽略，也就是说液相迁移只是引起了两端液相体积分数和孔隙率的变化，因此在液相共烧结模型计算过程中，需要使用液相迁移模型更新两端的液相体积分数，同时也要使用固相共烧结模型更新两端的实际烧结应力，然后不断迭代计算便可得到任意时刻共烧结体两端的黏结相和密度梯度分布情况.

1.3 数学模型

由液相共烧结物理模型可知，共烧结试样两端液相和密度梯度分布的计算只有数值解，故可采取有限元法求解，把每烧结10 s（dt）作为一个计算时间节点，在长度方向把共烧结试样两端都分成n段，然后以硬质耐火相颗粒半径、相对密度和液相体积分数为基本参数从室温升温烧结开始计算，根据两端基本参数的初始值以及温度变化可以更新迭代相应数值，不过在每个时间节点计算前，都需要先对两端界面处自由烧结收缩速率的大小进行判断，确定界面应力作用的方向，以求出两端在界面应力作用下的实际烧结应力.详细计算过程如图3所示，根据两端初始相对密度D0A、D0B、黏结相初始质量分数wt0A、wt0B以及硬质耐火相初始颗粒半径R0A、R0B，可以将整个计算过程分为以下三步：

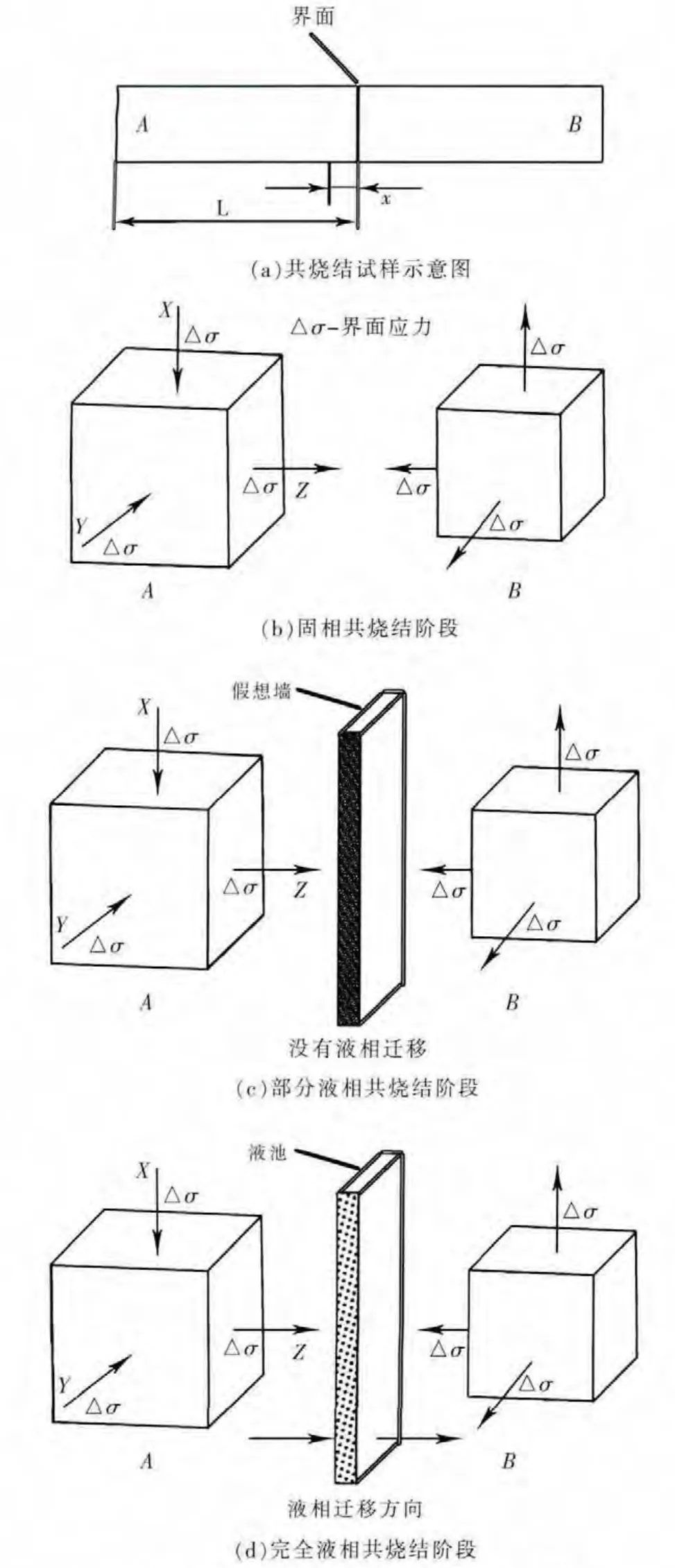
图2 液相共烧结不同阶段的物理模型

第一步是计算固相共烧结致密化过程，该过程没有形成液相，因此gA=gB=0，由方程（A-1）可知该阶段界面处两端的固相相对密度等于整体相对密度，即D0sA=D0A、D0sB=D0B，根据方程（A-6）可以得到两端界面处的体积黏度K0A、K0B，根据方程（A-4）可得到烧结开始0 s时界面处两端自由烧结的烧结应力σ0sA、σ0sB，根据方程（A-1～A-3）可得到界面处两端自由烧结的收缩速率D˙0fA、D˙0fB，根据方程（A-8）可得到界面处的界面应力Δσ0，根据方程（A-10）可得到0 s时界面处两端在界面应力作用下的实际收缩速率D˙0A、D˙0B，然后乘以烧结时间dt，就可以得到10 s时间后界面处两端相对密度的增量 ΔD0A、ΔD0B，然后与D0A、D0B相加即可得到10 s时间后两端的相对密度D10A=D0A+ΔD0A、D10B=D0B+ΔD0B，同样地根据方程（A-5）可得到10 s时两端硬质耐火相的颗粒半径R10A、R10B.这就完成了一个循环，如此循环迭代，就可以得到两端界面处在固相共烧结阶段任意时刻的相对密度数值，根据方程（A-9）可以得到其他位置相同时刻的相对密度数值.

第二步是计算部分液相共烧结致密化过程，设液相开始形成的第一个时刻为t1，根据物理模型可知该过程与固相共烧结类似，只是在使用方程（A-1）计算固相相对密度的时候不能再把两端的液相体积分数看成0，即gt1A≠0、gt1B≠0，需先根据与温度有关的函数求出t1时刻的液相体积分数g（t1）A、g（t1）B，然后根据方程 （A-1）便可得到两端界面处的固相体积分数D0sA＝D0A（1-g（t1）A）、D0sB＝D0B（1-g（t1）B），同样地，接下来全部按照第一步的步骤可以计算出（t1+10）s时界面处两端的相对密度D（t1+10）A、D（t1+10）B以及硬质耐火相的颗粒半径R（t1+10）A、R（t1+10）B.这就完成了一个循环，如此循环迭代，就可以得到两端界面处在部分液相共烧结阶段任意时刻的液相体积分数和相对密度数值，根据方程（A－9）可以得到其他位置相同时刻的液相体积分数和相对密度数值.

第三步是计算完全液相共烧结液相迁移以及致密化过程，设等温烧结第一个时刻为t2，根据物理模型可知该过程与部分液相共烧结致密化类似，所不同的是在计算液相体积分数时只需考虑液相迁移而不用考虑温度引起的变化，而且在t2时刻界面处两端的液相体积分数根据第二步结束时的计算结果可以得到，设为g（t2）A、g（t2）B，然后根据方程（A－1）便可得到两端界面处的固相体积分数D0sA＝D0A（1-g（t2）A）、D0sB＝D0B（1-g（t2）B），同样地，接下来全部按照第一步的步骤可以计算出（t2+10）s时界面处两端的相对密度D（t2+10）A、D（t2+10）B以及硬质耐火相的颗粒半径R（t2+10）A、R（t2+10）B，特别需要说明的是最后需要根据方程（A-7）更新下一个时间节点界面处两端的液相体积分数g（t2+10）A、g（t2+10）B.这就完成了一个循环，如此循环迭代，就可以得到两端界面处在完全液相共烧结阶段任意时刻的液相体积分数和相对密度数值，根据方程（A-9）可以得到其他位置相同时刻的液相体积分数和相对密度数值.

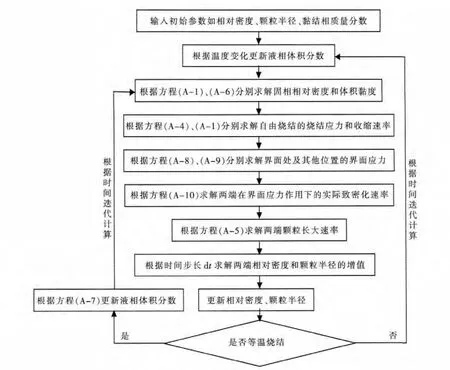
图3 液相共烧结模型计算过程示意图

然而在实际计算过程中，需要先根据两端自由烧结的收缩速率大小来判断界面应力的作用方向，为简化公式表示，现假设界面应力的作用方向一直不变，那么两端界面处整个计算过程可用以下部分公式进行表示：

以此类推，一直计算到时间t1，这时候黏结相开始形成液相但是没有发生迁移，假设使用F（T）来表示液相体积分数随着温度变化的函数，因此

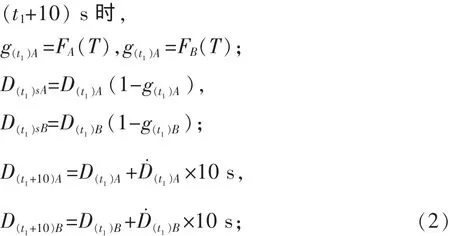
以此类推，一直计算到时间t2，这时候黏结相已经完全融化成为液相并开始迁移，假设使用P（g）来表示液相体积分数随着液相迁移变化的函数，因此

以此类推，一直计算到等温烧结结束，假设此时为t3，那么就可以得到两端界面处的液相体积分数g（t3）A、g（t3）B和相对密度数值D（t3）A、D（t3）B，根据液相体积分数可求出黏结相的质量分数，从而可以估算得到相应的理论密度 ρ（t3）Amax、ρ（t3）Bmax，最终得到相应的密度值 ρ（t3）A、ρ（t3）B：

同样地也可以得到其他位置相同时刻的液相体积分数、相对密度以及密度数值.

2 模型验证

假设A、B两端采用平均粒度分别为3 μm(R0A=1.5 μm)和 0.8 μm(R0B=0.4 μm)的 YG8 硬质合金混合料，按照与黏结剂按体积比58∶42放入XSM1/20-80混炼机中在温度170℃时混炼3 h并破碎，真空干燥8 h，采用HTSJ160B型夹层注射成型机制备均匀两层试验样品，并加工成5 mm×5 mm×36 mm长方体试样.压胚经过脱脂后相对密度分别为D0A=0.574、D0B=0.574，接下来将压胚进行真空烧结，其中烧结工艺如下：先以5℃/min加热到600℃保温60 min，然后以5℃/min升温至1 100℃保温40 min，最后以5℃/min加热到1 420℃保温60 min.采用EDX-GENESIS 60S能谱仪测量共烧结试样的元素分布，得到两端Co含量梯度分布.将真空共烧结后的试样切成9段如图4所示，再对每段试样密度进行测量，得到两端密度梯度分布.根据以上初始参数和附录B的相应数据，代入液相共烧结模型进行计算验证.

图4 试样分割示意图

2.1 Co相梯度

根据模型可以预测共烧结试样在1 420℃温度下烧结不同时间的Co相梯度分布如图5所示，可见随着时间的推移，Co相梯度分布趋向平缓，液相迁移压力梯度逐渐减小.

将模拟的数据与实验所测得的Co相含量梯度分布进行对比，结果如图6所示，从图6中可以看出共烧结试样在1 420℃下等温烧结60 min液相迁移的模拟结果与实验结果趋势一致.

图5 预测试样在1 420℃温度下烧结不同时间的Co相梯度分布图

图6 Co相含量梯度分布模拟与实验数据对比图

2.2 密度梯度

根据模型可以预测共烧结试样在任意位置任意时间的致密化过程，由于模拟计算过程中认为两端没有受到界面应力影响，因此将试样两端端点处以及界面处致密化曲线的模拟结果对比如图7所示，可见在界面应力和液相迁移的作用下，促进了界面处附近粗晶端的烧结而抑制了细晶端的烧结.

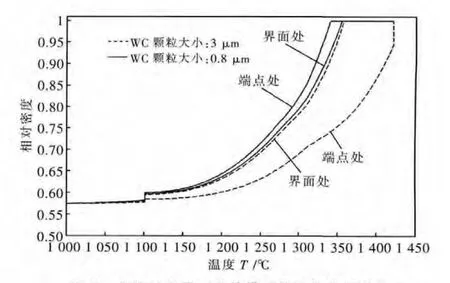
图7 两端以及界面处的模拟致密化曲线对比图

为进一步验证液相共烧结模型致密化规律，使用模型中方程（4）估算模拟密度的梯度分布，并与实验所测得的密度梯度分布对比如图8所示，可见模拟结果与实验结果符合很好.

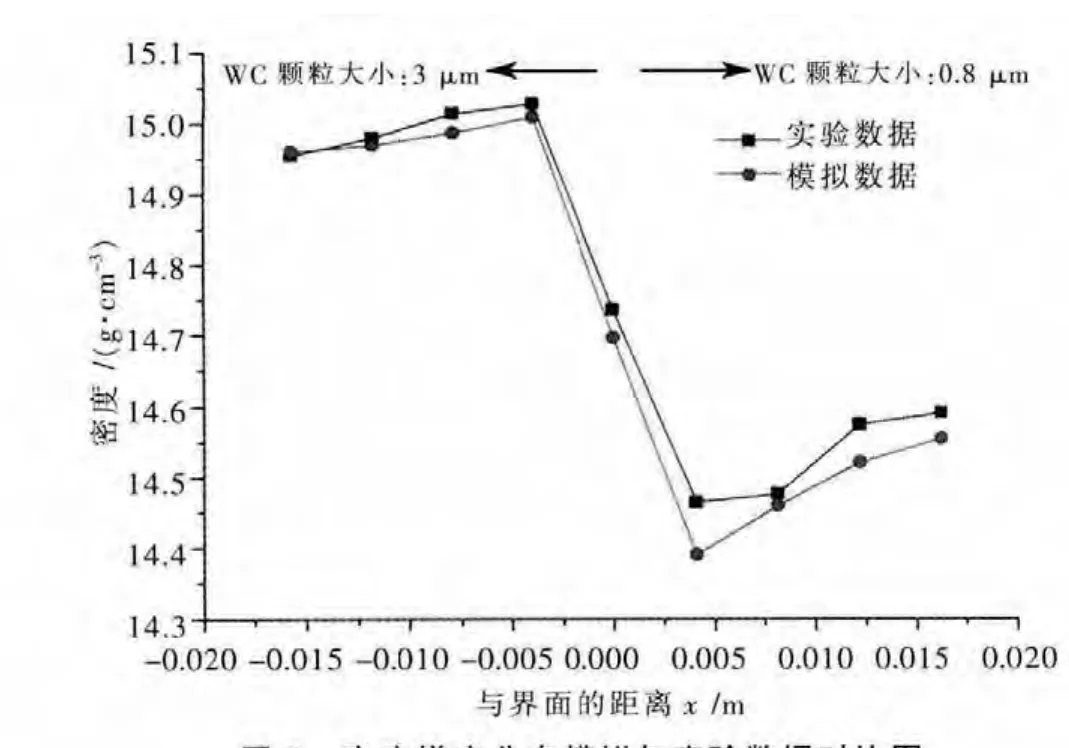
图8 密度梯度分布模拟与实验数据对比图

3 模型讨论

3.1 主要因素

在液相共烧结过程中，界面应力和液相迁移对两端烧结形成包括液相含量和密度的梯度分布至关重要.烧结前期两端不存在液相，只存在界面应力，为保持界面连续，界面应力会抑制收缩较快端的烧结而促进收缩较慢端的烧结，而且两端的收缩速率差异越大，则产生的界面应力越大，其作用会随着界面距离的增大而逐渐减弱，可见在烧结前期这个阶段的致密化是以界面应力的作用为主导；烧结后期两端已经高度致密化，虽然同时存在界面应力和液相迁移，而且液相迁移可能会引起界面应力的突变，然而由于体积黏度较大，两端致密化速率受到界面应力的影响很小甚至可以忽略，最后即使两端都达到全致密了，但是假如依然存在液相迁移压力梯度，液相还是会发生迁移，引起液相体积分数的变化，从而极大地影响了两端的致密化速率，可见在烧结后期这个阶段的致密化是以液相迁移的作用为主导.

简而言之，在液相共烧结法制备功能梯度材料的生产实践中，液相迁移对于两端最终液相以及密度的梯度分布具有较大的主导性作用，而界面应力对于最终的密度梯度分布影响较小，然而界面应力对于实际共烧结过程中界面的失效分析显得更为重要.

3.2 适用范围

液相共烧结模型是在液相烧结、液相迁移和固相共烧结模型的基础上提出来的，因此需要同时符合3个模型的基本假设，如液相烧结模型和固相共烧结模型都是基于黏弹性本构方程建立的；界面应力是基于连续介质不出现裂纹等宏观断裂缺陷的假设推导得到的，也就是说界面应力全部参与了致密化过程没有做其他形式的功；液相迁移模型要求固相骨架不是刚性的，从而随着液相体积的增减膨胀或者收缩，也就是说在边界移动的同时长度也会发生变化，而且系统不同位置只存在液相浓度梯度而不存在其他化学梯度；不同于常见的固-液-气三相系统，液相迁移的热力学驱动力是固液两相系统整体界面自由能的降低，即使在达到全致密不存在毛细管力的时候，只要存在液相迁移压力梯度，液相迁移依然会发生，因此在使用液相迁移模型的时候要求材料尽可能接近全致密；特别地，对于等温烧结才发生液相迁移的假设，实际上往往还没开始等温烧结就已经完全液化并发生迁移或者部分液化也会发生液相迁移，但是由于升温速度较快时间较短，在等温烧结前的液相迁移相对影响很小甚至可以忽略，例如模型验证的YG类硬质合金，液相出现到等温烧结只用了10多分钟，而将原来的等温烧结时间叠加20 min后再进行模拟，发现模拟结果与原来结果差别很小，因此验证了这个假设的合理性.

综上所述，液相共烧结模型需要满足以下假设：①基于黏弹性流动理论；②界面连续不出现裂纹等缺陷；③不是刚性的固相骨架；④不存在其他化学梯度；⑤出现液相到等温烧结的时间较短，而且在等温烧结时已高度致密化.

4 结 论

1）以颗粒半径、固相相对密度和液相体积分数为基本参数，建立了基于黏弹性理论的液相共烧结模型，并通过YG8硬质合金的实验加以验证，能较准确地预测密度梯度和Co相梯度分布情况.

2）造成液相共烧结梯度分布的主要原因是界面应力和液相迁移，烧结前期界面应力主导，而烧结后期液相迁移主导.如果只是粗略估算液相共烧结密度梯度分布可直接通过液相迁移模型进行简单估算.

3）液相共烧结模型可为梯度功能材料制备与结构优化设计提供理论依据，由于模型中的参数都具有物理意义，因此可进一步推广到其他双相结构复合材料的相关性能研究.

附录A

根据P.E.Mchugh等[16]的液相烧结模型可知，固相相对密度（也称为固相体积分数）增长速率，其中分别代表颗粒重排、液相熔化和烧结颈长大引起固相相对密度的变化速率，因此可得到整体相对密度D、固相相对密度Ds以及液相体积分数g的关系为：

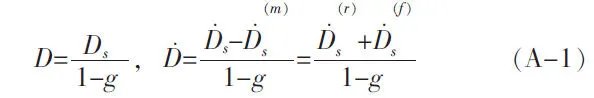
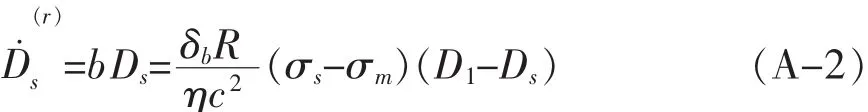
Ds为固相相对密度（如果），b是无量纲的因子 （b=1），δb为平衡状态的液体薄膜厚度（δb≈1.5 nm），R为固相颗粒半径，σs为烧结应力，σm为外加机械应力，η为液体黏度，c为烧结颈接触半径（根据几何关系可得c2=2R2δ）.此时，烧结颈长大引起固相相对密度的变化速率（f）为：

Ds为固相相对密度，δ为压应变，为应变速率，R是颗粒半径，Z是晶粒配位数，σs是烧结应力，σm是外加机械应力，Δp是气孔气压和外部气压的差（在计算过程中认为Δp=0），c是烧结颈接触半径 （根据几何关系可得c2=2R2δ），L是固相原子溶解析出反应速率常数，Ω是固相原子体积，k是波尔兹曼常数，T是温度，C1是烧结颈处液相中的固相原子浓度，δb是液相薄膜厚度（δb≈1.5 nm），Db是固相原子在液相晶界的扩散系数，一般认为LΩ和C1ΩδbDb是与温度有关的函数.在不考虑化学势存在的前提下，烧结应力σs主要包括毛细管力σ1和固液界面应力σs1，即：

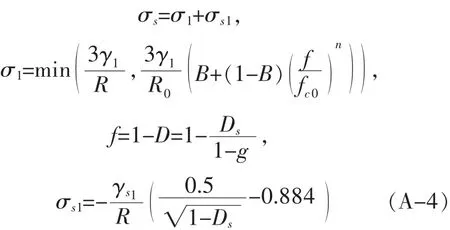
σ1促进烧结致密化，而σs1往往会阻碍烧结致密化，γ1为液相比表面能，f为孔隙率，fc0表示烧结后期大于2/3R0大孔隙的体积分数，B和n都是可调常数，γs1为固液界面的比表面能，R是颗粒半径，Ds为固相相对密度.此外，晶粒长大速率R˙会遵守以下演变方程为：

R是颗粒半径，γs1为固液界面的比表面能，L是固相原子溶解析出反应速率常数，Ω是固相原子体积，一般认为LΩ是与温度有关的函数.根据方程(A-1～A-5)可以得到体积黏度K为：

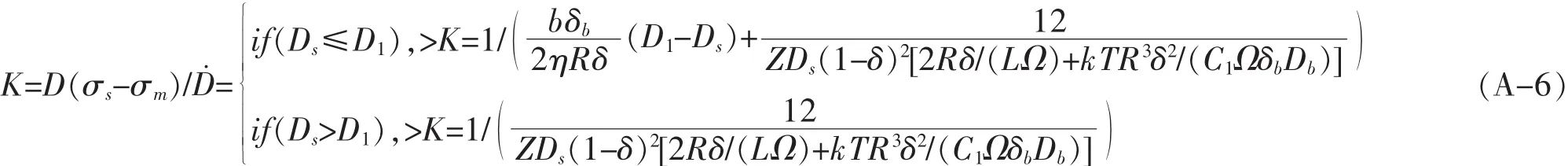
根据Zhigang Zak Fang等[17]的液相迁移模型可知，液相迁移控制方程为：

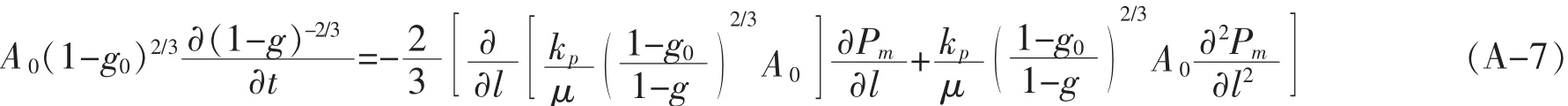
A0为液相迁移方向在初始时刻的横截面积（m2），t为时间（s），g为液相体积分数，g0为初始时刻的液相体积分数，l为液相迁移方向的距离（m），kp是液体渗透率（m2），μ 为液体黏度（kgm-1s-1），Pm为液相迁移压力（Pa）.特别说明一下，液相迁移控制方程是一个非线性微分方程，需要用到预测-修正的Mac-Cormack方法进行计算，具体可以参考文献[17].

根据何浩等[9]的固相共烧结模型可知，假设B端收缩速率较A端的要快，那么界面应力计算公式为：

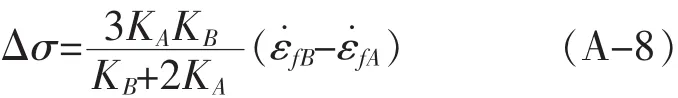
KA、KB分别为A端和B端的体积黏度，fA、fB分别为A端和B端自由烧结瞬时收缩速率，根据界面应力沿试样呈三次方分布逐渐递减的规律可知，界面应力在界面处为最大值Δσ，然后以三次方规律逐渐降低，那么离界面处距离x处的界面应力大小为：

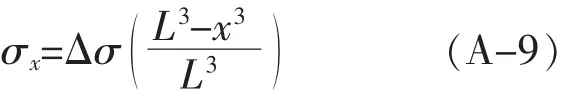
x为距离界面处的距离，L为试样界面到两端的距离（m），根据三向的受力分析可得界面处A、B两侧在界面应力作用下的实际致密化速率A、B分别为：

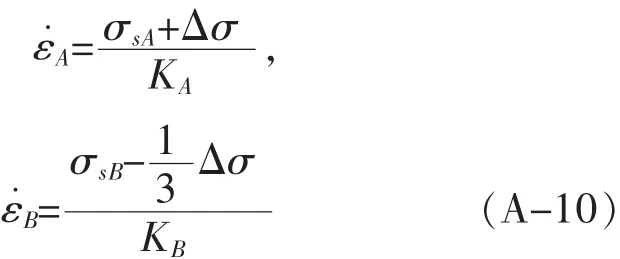
σsA、σsB分别为A端和B端自由烧结的烧结压力，界面应力在界面处为最大值Δσ，KA、KB分别为A端和B端的体积黏度.

附录B

根据Bjorn Uhrenius[20]的研究可知液相烧结的WC和Co的摩尔体积与温度的关系分别为：

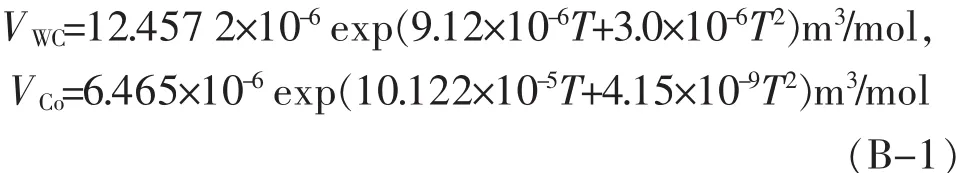
已知WC的摩尔质量MWC=196 g/mol，Co的摩尔质量MCo=59 g/mol，可得已知温度T的情况下在单位体积里Co相的质量分数wt和体积分数g相互转化的公式分别为：

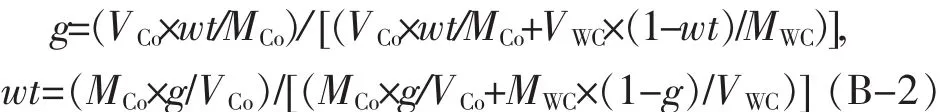
根据P.E.Mchugh[16]的研究可知WC-Co烧结体系液相烧结的相关数据，由于压胚初始密度较高，后期大孔隙的量很少，因此根据文献[21]可知fc0可取0.05，具体计算如下：

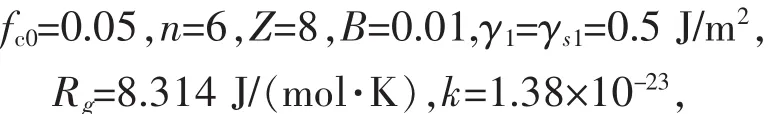
由于WC-Co烧结体系在还没达到Co相熔点之前就会形成大量柔软的Co-W-C合金颗粒来填充孔隙，也就是说在重排作用下能达到最大固相相对密度D1应该随着柔软的Co-W-C合金颗粒含量的增加而变大，又Co-W-C黏结相的体积分数是有关于温度的函数，因此方程（A-2）中的D1应该修正如下：

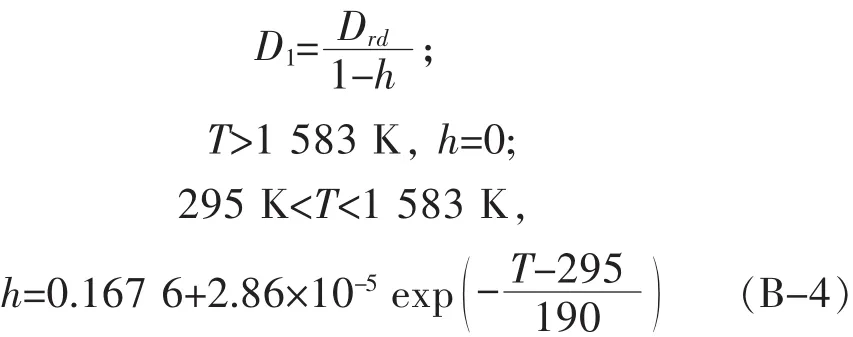
根据Zhigang Zak Fang[17]的研究可知，方程（A-7）中的液相迁移压力和渗透率计算如下：

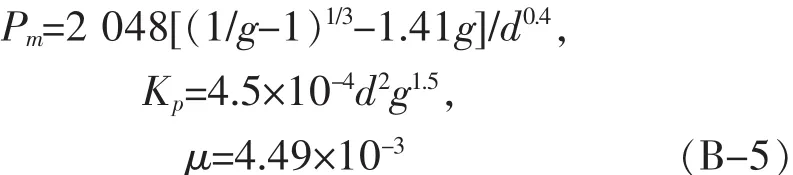
Pm是液相迁移压力 （Pa），g是液相体积分数，d是颗粒尺寸大小（m），Kp是渗透率（m2），μ 是 Co 液体黏度（kgm-1s-1）.

根据刘寿荣[22]的研究可知，由WC和Co组成无孔隙的理想致密体，则合金理论密度ρt可由下式进行估算：

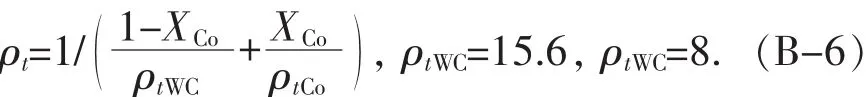
XCo其中表示 Co 相的质量分数，ρtWC、ρtCo分别代表WC和Co的理论密度（g/cm3）.

[1]张立,黄伯云,吴恩熙.双相结构梯度硬质合金的研究现状[J].材料导报,2000(12)：17-19.

[2]张文毓.硬质合金技术研究进展[J].材料开发与应用,2011,26(1)：61-65.

[3]羊建高,戴煜.硬质合金的发展趋势及特殊粉末的制备技术[J].稀有金属与硬质合金,2011(1)：48-51.

[4]张武装,刘咏,贺跃辉,等.涂层梯度硬质合金的研究进展[J].功能材料,2006,37(10)：1531-1534.

[5]邓福铭,陈启武.PDC超硬复合刀具材料及其应用[M].北京：化学工业出版社,2003.

[6]Simchi A.Densification and micro-structural evolution during co-sintering of Ni-base superalloy powders[J].Metallurgical and Materials Transactions A,2005,37(8)：2549-2557.

[7]FirouzdorV,imchiA,KokabAH.Aninvestigationofthedensification and micro-structural evolution of M2/316L stepwise graded composite during co-sintering [J].Journal of Materials Science,2008,43(1)：55-63.

[8]Firouzdor V,Simchi A.Co-sintering of M2/17-4PH powders for fabrication of functional graded composite layer[J].Journal of Composite Materials,2010,44(4)：417-435.

[9]何浩.粉末共注射成形及共烧结过程的研究[D].长沙：中南大学,2010.

[10]刘攀,何浩,李益民.基于黏弹性理论异种材料的共烧结致密化[J].中国有色金属学报,2011,21(6)：1389-1395.

[11]Maximenko A,Roebben G,Van O.Modelling of metal-binder migration during liquid-phase sintering of graded cemented carbides[J].Journal of Materials Processing Technology,2005,160(3)：361-369.

[12]Cooper R.烧结制造硬质合金复合材料时各层显微组织和性能演变的模型[C]//第十一届普兰西会议论文集,株洲：硬质合金编辑部,1985：323-329.

[13]刘咏,杨建高.梯度与新型功能梯度硬质合金[M].长沙：中南大学出版社,2010：117-119.

[14]程继贵,吴玉程,夏永红，等.层压法制备双层晶粒WC-Co梯度功能材料的研究[J].功能材料,2001,10(1)：1252-1256.

[15]Svoboda.J,Riedel H,Gaebel R.A model for liquid phase sintering[J].Acra mater,1996,44(8)：3215-3226.

[16]Mchugh P E,Riedel H.A liquid phase sintering model：Application to Si,N,and WC-Co[J].Actamuer,1997,45(7)：2995-3003.

[17]Fan P,Fang Z G Z,Sohn H Y.Mathematical modeling of liquid phase migration in solid-liquid mixtures：Application to the sintering of functionallygradedWC-Cocomposites[J].ActaMaterialia,2007,55：3111-3119.

[18]吴冲浒.WC-Co系硬质合金Co相的熔点[J].1994-2008 China academic journal electronic publishing house,1999,16(4)：201-205.

[19]Gillia O,Bouvard D,Phenomenological analysis of densification kinetics during sintering：Application to WC-Co mixture[J].Materials Science and Engineering,2000,279：185-191.

[20]Bjorn U.Evaluation of molar volumes in the Co-W-C system and calculation of volume fractions of phases in cemented carbides[J].Refractory Metals&Hard aterials,1993-1994,12：121-127.

[21]Maximenko A,Roebben G,Van Der Biest O.Modelling of metalbinder migration during liquid-phase sintering of graded cemented carbides[J],Materials Processing Technology,2005,160：361-369.

[22]刘寿荣.WC-Co硬质合金成分的磁性测定原理[J].硬质合金,1998,16(3)：129-135.