数字全息显微术应用于微器件的测量研究*
2014-12-26王红军李方方
王红军,李方方
(西安工业大学 光电工程学院,西安710021)
早在1948年英国物理学家丹尼斯·伽伯(D.Gabor)提出全息术的设想后[1],用水银灯发出的可见光代替电子波,获得了第一张全息图及其再现像.但是由于光源相干性的限制以及“孪生像”的问题,全息术的研究进展比较缓慢,直到1960年世界第一台激光器问世以后,激光作为一种高相干度的光源,推动了数字全息术的发展.1962年,利思(Leith)和厄帕特尼克斯(Upatnieks)将通信技术中的载频概念应用到空域中,首次提出了离轴全息的概念[2].随着计算机技术的发展,人们逐渐将其运用到全息术中,数字全息术应运而生.1967年J.W.Goodman和R.W.Lawrence提出了数字全息术[3],开辟了全息应用的新领域.20世纪90年代后期,随着计算机技术的进步和高质量电荷耦合器件CCD的出现,逐渐出现了基于复振幅位相定量分析的数字全息显微成像技术,结合了计算机再现技术和光学显微技术,可实现反射或透射物体的三维微观轮廓测量[4-5].该方法可定量分析样品的幅度和位相信息,为样品的定量检测分析带来了极大的方便.
数字全息术的迅猛发展使其应用领域得到广泛拓展,其中显微测量是最具有潜力的应用领域,相比其它测量技术具有系统简单、非接触、无损伤的特点[6].其应用已涉及到很多研究领域,如微光学、生物芯片、激光加工、生命科学、医疗诊断等[7-8].如利用数字全息显微技术可实现微器件形变测量的目的,包括受力压迫,温度变化,静电影响导致的形变,通过测量可以得到它的微小形变或者微小位移,进而反馈到实际的调节中,在提高准确率的同时大大节约了时间.下面对数字全息显微技术应用于微器件的测量方面进行具体的研究分析.
1 数字全息的记录与再现
图1所示为数字全息显微系统的原理图.光纤耦合激光器(波长λ=650nm)发出的光束,经分束器后分为两束光,一束用来照射待测样本,经调制后因携带有待测样本的信息形成物光波O,另一束直接照射到平面反射镜作为参考光波R,两束光波在CCD光敏面上干涉形成全息图,通过调节反射镜的位置,可改变物光波和参考光波之间的夹角,从而得到高质量的全息图.
CCD记录平面上的光强分布为

其中O*,R*分别是物光波和参考光波的共轭光波,经CCD抽样离散处理后的光强为
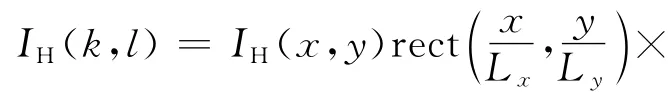
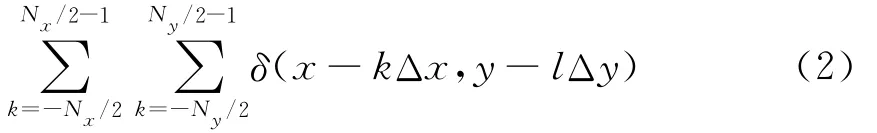
其中Lx,Ly为CCD的光敏面大小,Δx,Δy为像素大小,Nx,Ny为CCD像素数.
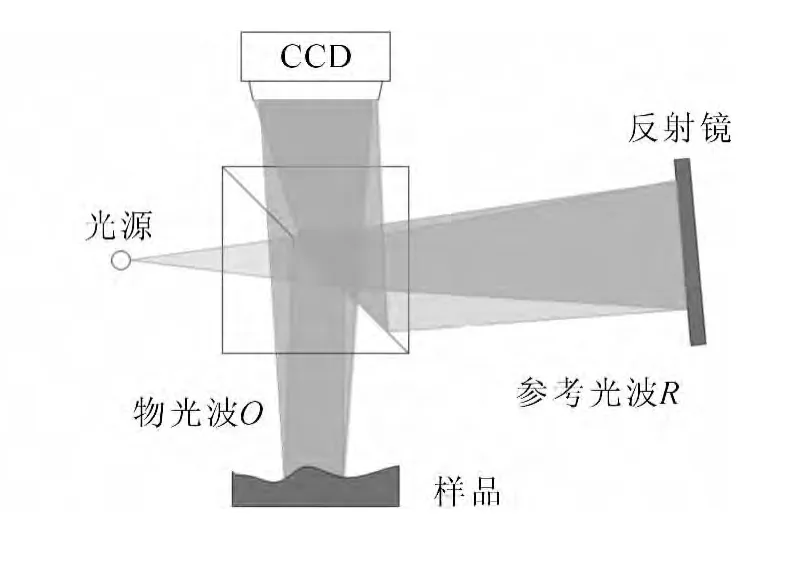
图1 数字全息显微实验光路Fig.1 Optical path of digital holographic microscopy experiment
在数字全息中,全息图可看作一孔径,物光波的重现就是参考光波经过孔径衍射的结果.图2是数字全息记录和再现示意图.
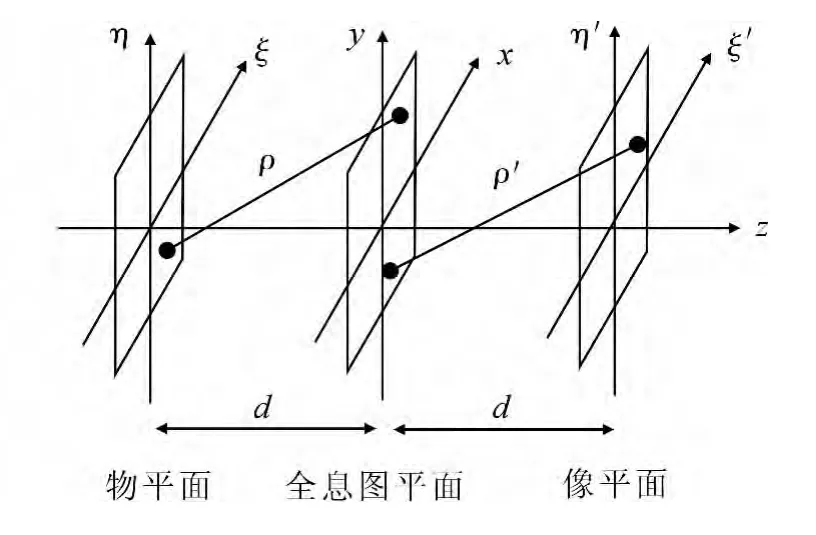
图2 数字全息记录和再现示意图Fig.2 Recording and reconstruction of digital holography
当用相干光波照射全息图时,衍射光波可近似用菲涅耳-基尔霍夫积分为
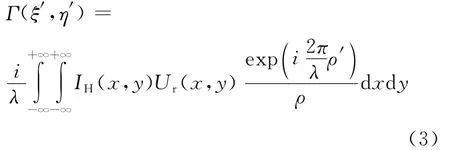
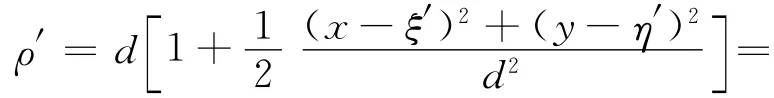
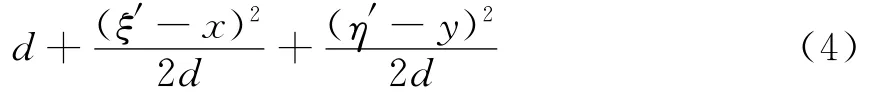
由于坐标x,y的值远远小于距离ξ′,η′,式(3)中的分母ρ′用d代替,再把式(4)代入,可以得到
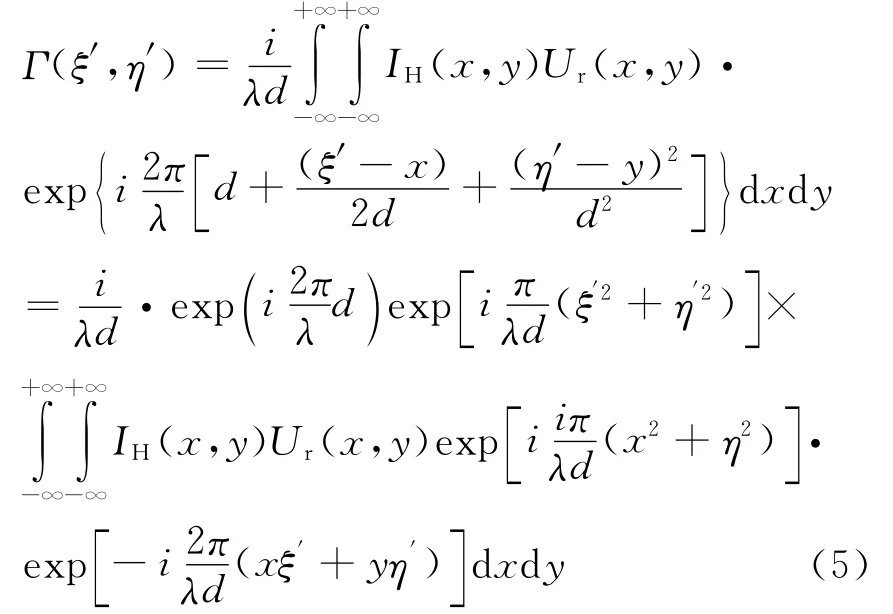
然后利用快速傅里叶变换FFT计算,进行后续的离散化处理.可以看出,在菲涅耳近似算法中,只用了一次快速傅里叶变换,如果把全息图平面所在的坐标看作空域坐标,那么重建像平面则位于空间频率域,重建图像中每个像素所代表的空间尺寸大小由重建距离d和所用波长λ决定.
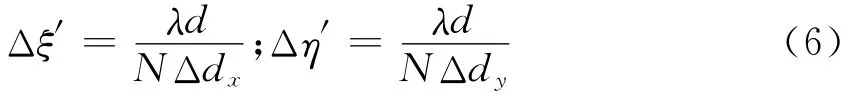
2 零级项和共轭像的抑制
在同轴全息中,三个衍射像频谱相互重叠,最终导致再现物光场不清晰,严重影响成像质量,而在离轴数字全息中,虽然可以实现零级、+1和-1级衍射像分离[9].但是由图3可以明显看到零级像的严重干扰,它位于像光场的中心,本身占据绝大部分的光能量,形成一个大的亮斑,造成另外两个衍射像黯淡,使再现像的质量严重下降,不宜观察与测量.随着再现距离的增大,再现像会越来越不清晰,当再现距离较近(接近于记录距离75mm)时,再现像的细节还是清晰可辨的,但是零级项、再现像和共轭像相互重叠,无法分离,而随着距离的增大,三者逐渐分离开来,像质会变得模糊.由此也验证了菲涅耳重建算法的重建图像像素大小是受重建距离影响的.
迄今为止,已经存在多种消除零级像和共轭像干扰的有效方法,比较常用的有如下几种:频域滤波法、空间滤波法和全息图减平均法,早期还提出全息图减零级强度和四步相移全息法[10-11],但后面这两种方法都需要记录多幅全息图,不适合于实时记录,而且对环境要求比较高.所以针对不同方法的优缺点,经过对待测样本结构特点进行分析,采用频域滤波法实现零级像和共轭像的消除.图4为全息图消除零级像和共轭像的过程.在滤波过程中,选择+1级频谱并将其移动到频谱的中心,然后进行傅立叶逆变换就可以获得预处理后的全息图,对该全息图进行再现就可以得到消除了零级像和共轭像的再现像.

图3 不同重建距离下的衍射像Fig.3 Diffraction of different reconstruction distance

图4 全息图去除背景光和共轭像Fig.4 Removing background light and conjugate image of hologram
3 实验结果和分析
为了保证全息图的质量,全息显微测量中需考虑物光和参考光的夹角.由奈奎斯特的采样定理可知,为保证图像采样的准确性,在一个条纹的周期内采样点不能少于两个[12].干涉条纹的间距要大于或等于CCD上两个像素点的大小,即
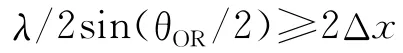
当参考光和物光的夹角θOR非常小时,近似sin(θOR/2)≈θOR/2,可得θOR/2≤λ/2Δx,即物参光的夹角范围为θ≤λ/2Δx,物参光夹角的大小和实验所用的激光器波长λ及CCD的像素大小有关.
实验中光源的波长λ=650nm,CCD像素为1 280×960,像元大小为Δx=4.65μm,则可计算得到物参光的最大夹角θmax=4°.因此为了能够得到高质量的全息图,保证再现像的质量,参考光和物光的夹角必须在很小的范围内,但同时参物光夹角的选取还要考虑到频谱分离条件,在离轴数字全息记录中,为实现零级,+1,-1级衍射像分离的目的,必须使物光和参考光倾斜一定角度,如果物参光夹角过小,则条纹比较稀疏,频谱+1、-1级和直流分量会发生重叠,再现像的噪声就比较大.
以MEMS刻线光栅为目标,调节反射镜使物光波与参考光波的夹角满足实验条件,用CCD记录得到的数字全息图.由CCD记录得到的数字全息图经过傅里叶变化得到其频谱图,用矩形滤波窗函数对进行滤波,得到只包含原始物光波的频谱,然后对其进行傅立叶逆变换得到消除噪声后的的全息图,最后重建出物光波,对应的重现距离值为75.50mm,获得了物光波的振幅和位相信息.图5为全息图和相应的处理结果.图5(b)可知,由于选取了合适的物参光夹角,零级像和±1级衍射像得到了很好的分离,图5(c)~5(d)为再现后包裹相位图和解包裹相位图,从相位图可用获取样本的轮廓信息.从位相图可重建出物体的轮廓信息,如图5(e)所示.图5(f)给出了图5(d)解包裹相位图在一个截面上的二维轮廓分布,可以得到MEMS器件的刻槽深度大约为160nm,栅距为430μm.
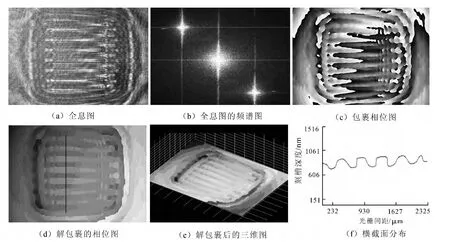
图5 全息图的再现结果Fig.5 Reconstruction result of numerical hologram
4 结 论
1)对不同重建距离下衍射像进行模拟,验证了菲涅耳重建算法的重建图像的像素大小由重建距离和所用波长决定的.
2)对物参光的夹角进行了分析研究,得出物参光的最大夹角θmax=4°,从而提高全息图质量,降低再现像的噪声.
3)用滤波的方法对零级项和孪生像进行了消除,继而进行重建,获得样品的定量位相信息,相比于传统测量方法具有非接触,无损伤,实时监测的特点.
[1] GABOR D.A New Microscopic Principle[J].Nature,1948,161:777.
[2] LEITH E,UPATNIEKS J.Reconstructed Wave Fronts and Communication Theory[J].Opt,1951,52:1123.
[3] GOODMAN J W,LAWRENEE R W.Digital Image for Mulation from Electronieally Detected Holograms[J].Opt,1967,11(3):77.
[4] CHARRIERE F,KUHN J,COLOMB T,et al.Characterization of Microlenses by Digital Holographic Microscopy[J].Applied Optics,2006,45(5):829.
[5] 钟丽云,张以谟,吕晓旭,等.数字全息中的一些基本问题分析[J].光学学报,2004,24(4):465.ZHONG Li-yun,ZHANG Yi-mo,LV Xiao-xu,et al.Analysis of Some Fundamental Issue about Digital Hologram[J].Acta Optica Sinica,2004,24(4):465.(in Chinese)
[6] 周文静,于瀛洁,陈明仪.数字全息显微测量技术的发展与最新应用[J].光学技术,2007,33(6):870.ZHOU Wen-jing,YU Ying-jie,CHEN Ming-yi.Recent Developments and Applications of Digital Micro-Holography[J].Optical Technique,2007,33(6):870.(in Chinese)
[7] 王云新,王大勇,赵洁,等.基于数字全息显微成像的微光学元件三维面形检测[J].光学学报,2011,31(4):0412003.WANG Yun-xin,WANG Da-yong,ZHAO Jie,et al.3DProfile Measurement for Micro-Optical Component by Using Digital Holographic Microscopy[J].Acta Optica Sinica,2011,31(4):0412003.(in Chinese)
[8] COLOMB T,CUCHE E,CHARRIERE F,et al.Automatic Procedure for Aberration Compensation in Digital Holographic Microscopy and Applications to Specimen Shape Compensation[J].Applied Optics,2006,45(5):851.
[9] 李俊昌,张亚萍,许蔚.高质量数字全息波面重建系统研究[J].物理学报,2009,58(8):5385.LI Jun-Chang,ZHANG Ya-Ping,XU Wei.High Quality Digital Holographic Wave-Front Reconstruction System[J].Acta Physica Sinica,2009,58(8):5385.(in Chinese)
[10] 马建设,任振波,苏萍,等.全息再现中几种消零级方法的像质评价及其改进[J].半导体光电,2013,34(4):713.MA Jian-she,REN Zhen-bo,SU Ping,et al.Comparison and Improvement of Image Quality Evaluation of Zero-order Elimination Methods in Holographic Reproduction[J].Semiconductor Optoelectronics,2013,34(4):713.(in Chinese)
[11] 候瑞宁,闫友房.离轴数字全息零级像和共轭像的消除方法[J].激光技术,2012,36(5):632.HOU Rui-ning,YAN You-fang.Elimination Method of Zero-Order Image and Conjugate Image of Off-Axis Digital Hologram[J].Laser Tehnology,2012,36(5):632.(in Chinese)
[12] LI Y.Digital Holography and Optical Contouring[D].Liverpool:Liverpool John Moores University,2009.
