单脉冲作用下在轨拦截器覆盖范围研究

武健，刘新学，舒健生，李亚雄，闫建峥

(1.第二炮兵工程大学906教研室，陕西西安710025;2.中国人民解放军96251部队，河南洛阳471003)

0 引言

轨道机动是动能型在轨拦截器对目标航天器实施拦截作战的前提，脉冲轨道机动在工程上易于实现，是各种轨道机动设计的基础［1-2］。为保证机动轨道设计和优化的可行性，在脉冲轨道机动设计与优化前，应该考虑目标航天器是否在在轨拦截器覆盖范围内。

文献［2］研究了在卫星轨道上任意一点施加大小固定、方向任意的脉冲后生成轨道的可达区域。文献［3］考虑脉冲幅值较小、生成轨道为椭圆轨道的情况，对初始轨道上任意点施加平面内幅值固定、方向任意的脉冲后卫星的机动范围进行了研究，所得结论适用于初始轨道为圆轨道和小偏心率椭圆轨道的情况。文献［4］推导了施加脉冲后生成轨道的运行规律，提出了利用优化理论确定卫星可达范围边界的方法，可用于初始偏心率较大的椭圆轨道。文献［5］利用包络线的方法确定了卫星在轨道平面内的可达范围。目前，这些理论研究大都集中于平面脉冲作用下卫星可达范围的确定［6-7］，但对任意方向单脉冲作用下卫星的可达范围研究较少。

本文围绕单脉冲作用下在轨拦截器覆盖范围展开研究，将初始轨道分为圆轨道和椭圆轨道，研究了单脉冲作用下在轨拦截器覆盖范围及描述形式。

1 模型假设与坐标系定义

本文研究中作如下假设:

(1)地球为均匀圆球，半径Rc=6 371 km;

(2)只考虑地球引力，忽略其他摄动力的影响;

(3)脉冲施加过程瞬间完成，忽略脉冲施加过程中在轨拦截器位置的变化;

(4)在轨拦截器提供的脉冲幅值较小，可提供大小不超过Δvmax、方向任意的脉冲。

本文研究主要在近焦点坐标系下，同时为了数学描述简捷，设计了一种近焦点坐标系球面坐标表示形式。

(1)近焦点坐标系

以轨道焦点为坐标原点，xy平面为轨道平面且x轴从焦点指向近地点，z轴与角动量方向一致，y轴与x轴和z轴构成右手正交坐标系［8］。

(2)近焦点坐标系的球面坐标描述形式

如图1所示，定义近焦点坐标的球面坐标形式为(ρ，φ，θ)，ρ为某矢量 T 的模;φ 为矢量 T 与其在xOy投影T'夹角;θ为T'与Ox轴夹角。

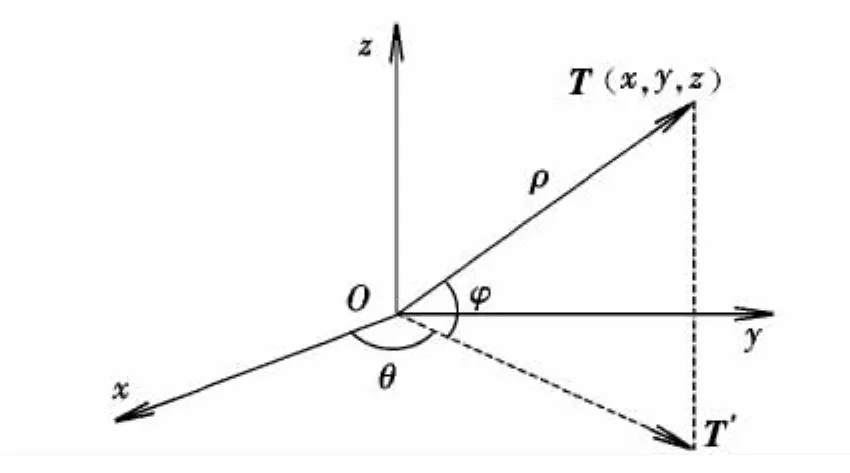
图1 近焦点坐标系的球面坐标形式Fig.1 Spherical coordinate of near focus coordinate system

球面坐标与直角坐标的转化关系为:

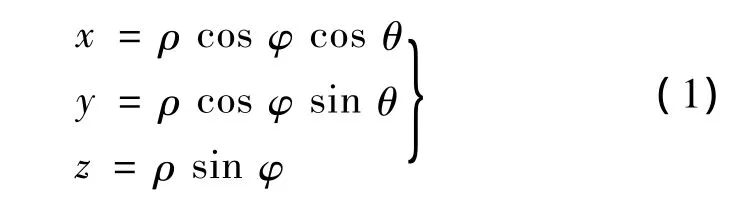
2 圆轨道在轨拦截器覆盖能力

脉冲Δv可分解为在轨道面内的脉冲ΔvR及垂直轨道面方向的脉冲ΔvW，且满足:

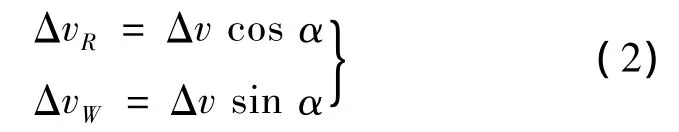
式中，α为脉冲矢量与其在轨道面的投影夹角。

2.1 平面脉冲作用下在轨拦截器覆盖范围

平面脉冲ΔvR作用下，利用活力公式推导出脉冲施加前后在轨拦截器的半长轴 a0和 af，具体为［9］:

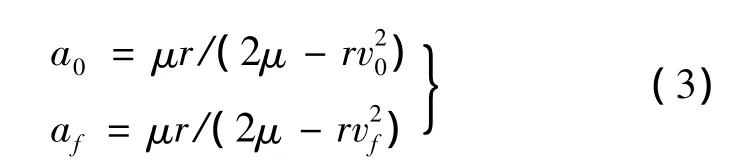
式中，μ为地球引力常数，r为脉冲施加时刻在轨拦截器的地心距;v0，vf为脉冲施加前后在轨拦截器的速度大小。vf计算如下:

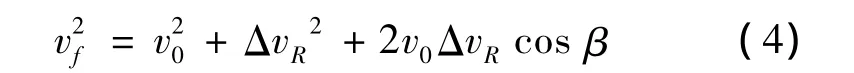
式中，β为脉冲矢量ΔvR与速度矢量v0的夹角。

脉冲施加前后在轨拦截器半长轴改变量为:

分析可知，Δa为vf的单调递增函数，当β=0且ΔvR=Δvmax时，半长轴增加最大;当β=π且ΔvR=Δvmax时，半长轴减少最大。由于圆轨道的特性(轨道上各点的地心距、速度大小都相等)，则在轨道上每一点施加大小相同、方向与该点速度方向一致(相反)的速度脉冲后，在轨拦截器生成轨道的地心距最大值(最小值)相等。初始轨道为圆形轨道时，平面单脉冲作用下在轨拦截器覆盖范围为一圆环，用球面坐标描述为:

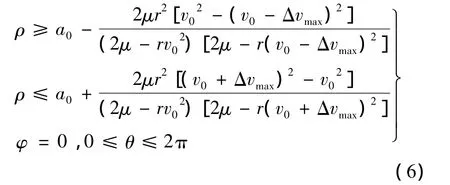
2.2 垂直轨道面脉冲作用下在轨拦截器覆盖范围

在垂直轨道面脉冲ΔvW作用下，轨道半长轴的变化Δa及轨道倾角变化Δi计算公式为:

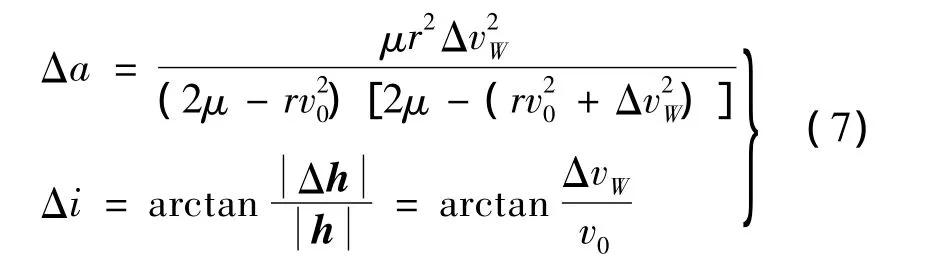
式中，h为角动量;Δh=r×ΔvW，为角动量改变量。

由于圆轨道的特征，在任意点施加方向、大小相同的垂直轨道面脉冲，在轨拦截器生成轨道地心距最大值(最小值)相等，垂直轨道面脉冲引起轨道倾角变化且大小相同。因此，垂直轨道面脉冲作用时，在轨拦截器覆盖范围为一曲面绕z轴旋转形成的区域，用球面坐标描述如下:

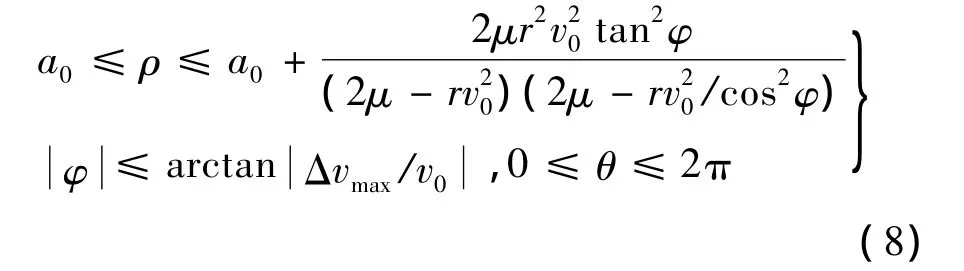
2.3 单脉冲作用下圆轨道在轨拦截器覆盖范围

任意方向、大小单脉冲作用时，可看成两个过程的叠加，平面脉冲改变轨道半长轴，垂直轨道面脉冲改变轨道倾角和轨道半长轴。综合2.1节和2.2节模型可得在轨拦截器覆盖范围为一曲面绕z轴旋转形成的包络区域，数学描述为:

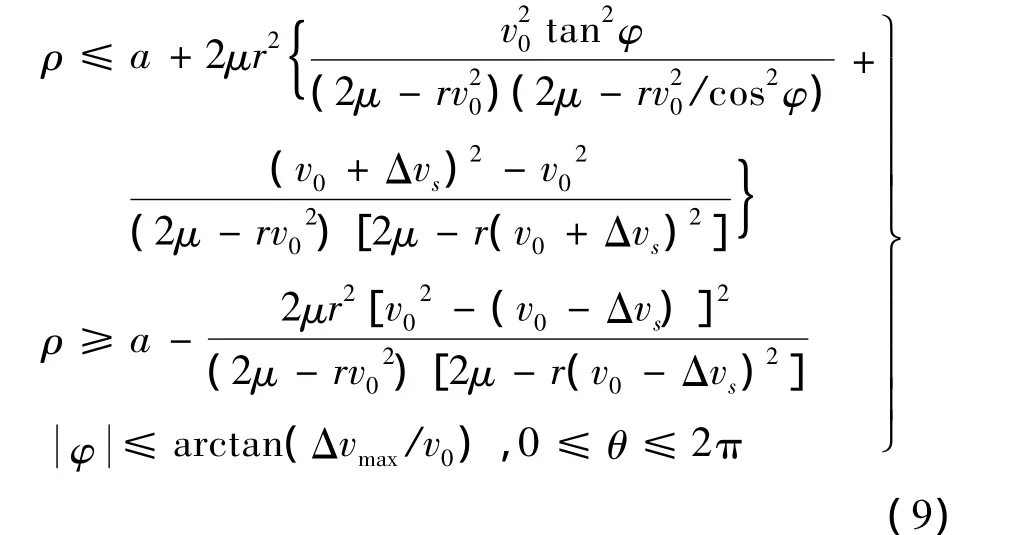
3 椭圆轨道在轨拦截器覆盖能力

3.1 平面脉冲作用下在轨拦截器覆盖范围

平面脉冲ΔvR作用下，在轨拦截器生成轨道的动量矩 h1和偏心率e，计算如下［10-11］:

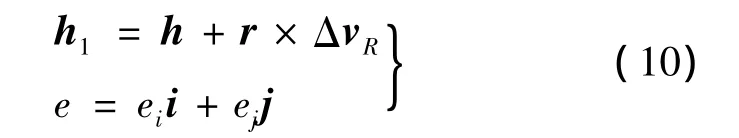
式中，i，j为近焦点坐标系 x，y轴的单位矢量;ei，ej为偏心率e在x，y轴的分量值，计算如下:

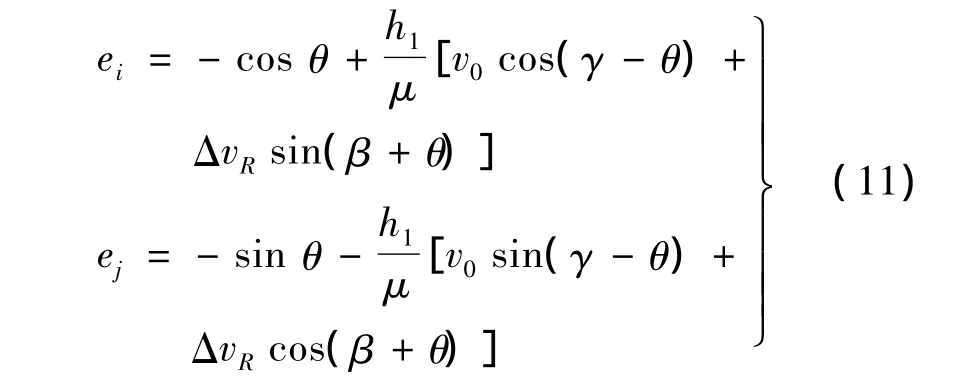
式中，θ为脉冲施加点的真近点角;γ为脉冲施加点在轨拦截器速度矢量与矢径垂线方向夹角。

θ，β 在［0，2π)变化时生成轨道曲线族［5］，生成的轨道半径统一描述为:

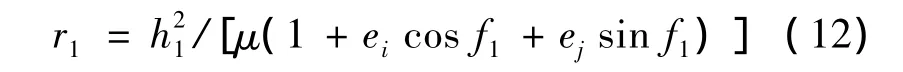
式中，f1为生成轨道上某点矢量与x轴夹角。

根据包络线的定义，曲线族的包络线即为在轨拦截器覆盖范围的边界。在轨拦截器覆盖范围的内外边界计算［5］如下:

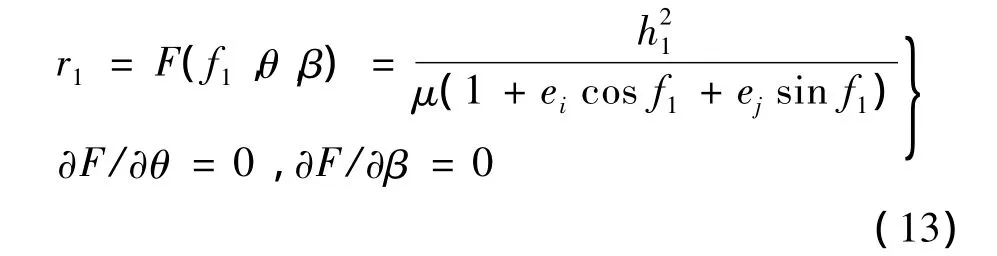
对上式进行求解，得到平面脉冲作用下在轨拦截器覆盖范围，具体求解过程参见文献［5］。

3.2 垂直轨道面脉冲作用下在轨拦截器覆盖范围

初始轨道为椭圆轨道，在垂直轨道面的脉冲作用下，用位置矢量描述在轨拦截器的覆盖范围较为复杂，本节用轨道根数描述垂直轨道面脉冲作用下在轨拦截器的覆盖范围。

在垂直轨道面脉冲作用下，根据高斯摄动方程得到在轨拦截器的轨道根数变化如下:

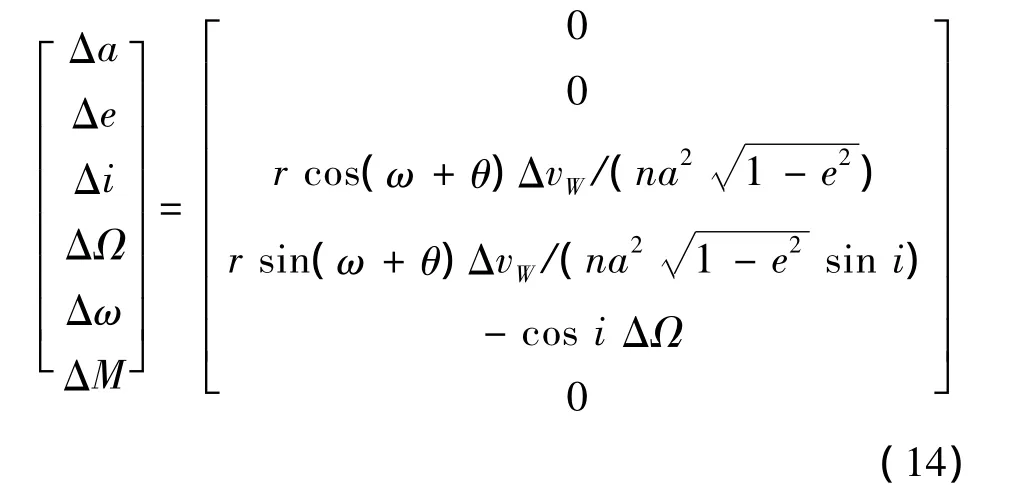
式中，Δa，Δe，Δi，ΔΩ，Δω，ΔM 为轨道根数变化量;n为平均运动常数。暂不考虑高斯摄动方程极值点情况，从式(14)可以得出，Δi，ΔΩ，Δω中两个变量独立。选Δi，ΔΩ作为描述在轨拦截器覆盖范围的参数，它们满足:

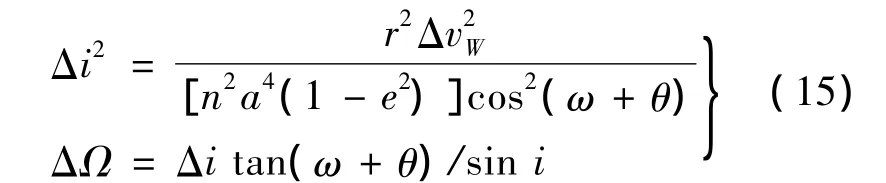
3.3 单脉冲作用下椭圆轨道在轨拦截器覆盖范围

在轨拦截器初始轨道为椭圆轨道，当有任意方向、大小的单脉冲作用时，可把该冲量看成平面脉冲和垂直轨道面脉冲的叠加。综合3.1节和3.2节模型，将(Δi，ΔΩ，r)作为描述在轨拦截器覆盖范围的参数。Δi和ΔΩ确定时，施加脉冲真近点角θ的位置确定，则式(13)退化为:

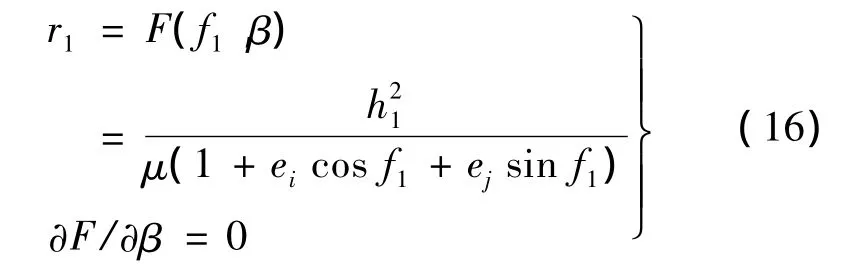
对上式求解，得到真近点角θ与β的关系［5］，联立式(15)得到单脉冲作用下在轨拦截器覆盖范围的数学描述如下:

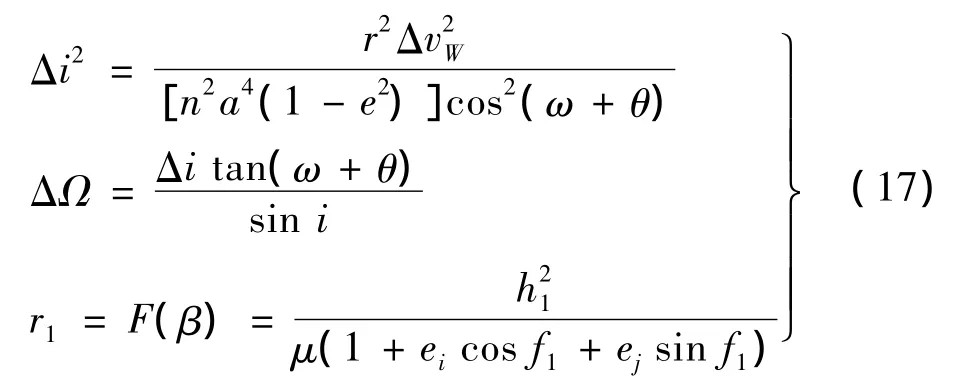
4 仿真计算及结果分析

4.1 初始轨道为圆轨道的情况

仿真条件取为:r=8 000 km，v=7.059 km/s，Δvmax=0.3 km/s。图2给出了平面脉冲作用下在轨拦截器的覆盖范围。

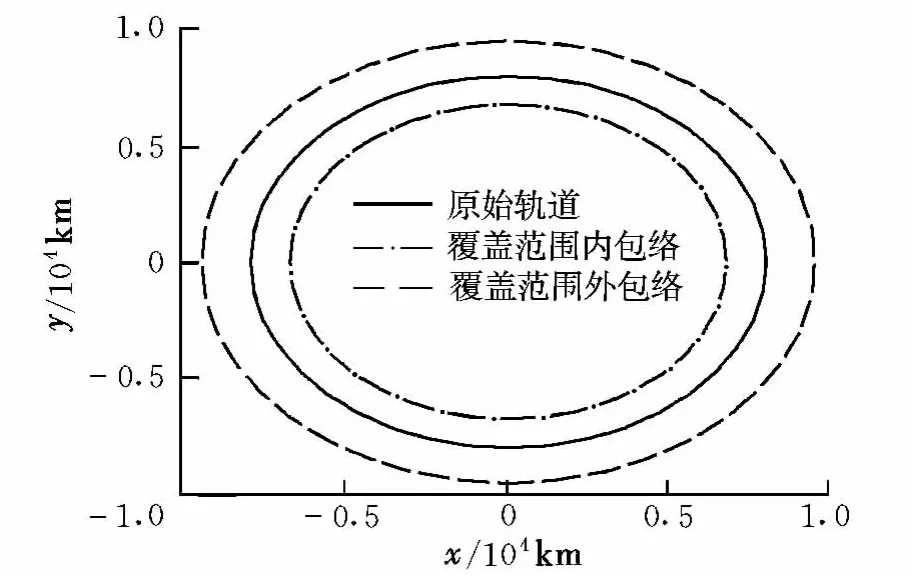
图2 在轨拦截器覆盖范围(平面脉冲)Fig.2 Coverage area of orbit-interception(coplanar impulse)

垂直轨道面脉冲作用下为绕近焦点坐标系z轴的旋转体，沿z轴且x＞0切面如图3所示。

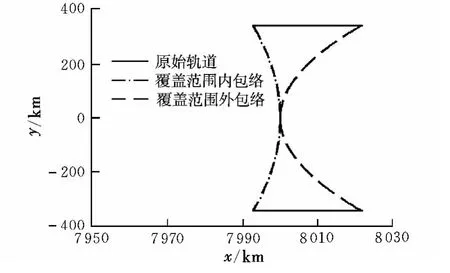
图3 覆盖范围切面图(垂直轨道面脉冲)Fig.3 Section diagram of coverage area(vertical impulse)

任意方向、大小单脉冲作用下，在轨拦截器的覆盖范围也是绕近焦点坐标系z轴的旋转体，沿z轴且x＞0切面如图4所示。

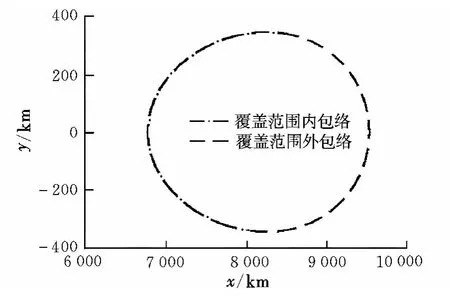
图4 覆盖范围切面图(任意方向)Fig.4 Section diagram of coverage area(any direction)

4.2 初始轨道为椭圆轨道的情况

仿真条件设置为:(a，e，i，Ω，ω，M)=(20 000 km，0.5，30°，45°，60°，0°)，Δvmax=0.3 km/s。图 5给出了平面脉冲作用下在轨拦截器覆盖范围。垂直脉冲作用下Δi，ΔΩ的变化范围如图6所示。任意方向、大小作用下，ΔΩ=0时在轨拦截器覆盖范围如图7所示。图8给出了ΔΩ=0时在轨拦截器覆盖范围。

从仿真结果可以看出，当最大变轨能力给定时，利用文中方法可以快速确定单脉冲作用下在轨拦截器的覆盖范围。

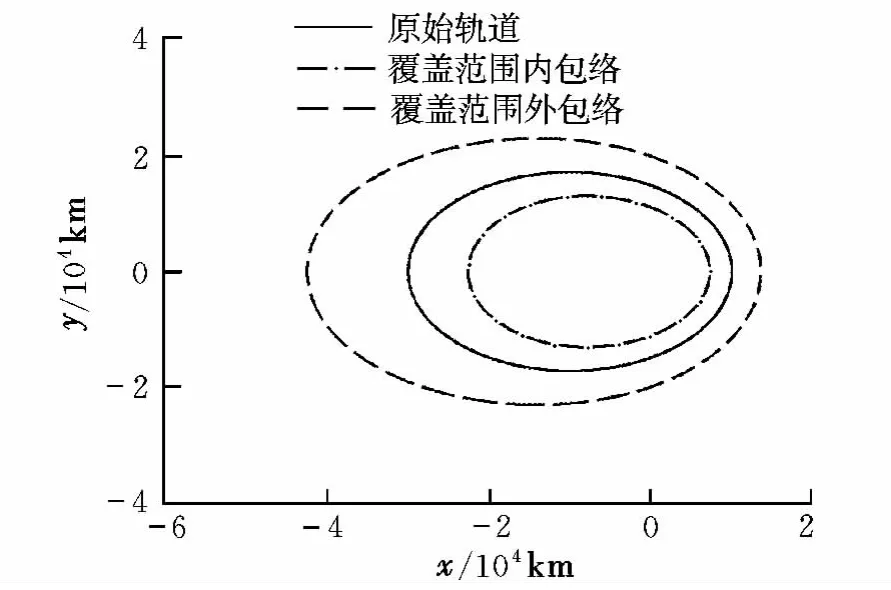
图5 在轨拦截器覆盖范围(平面脉冲)Fig.5 Coverage area of orbit-interception(coplanar impulse)

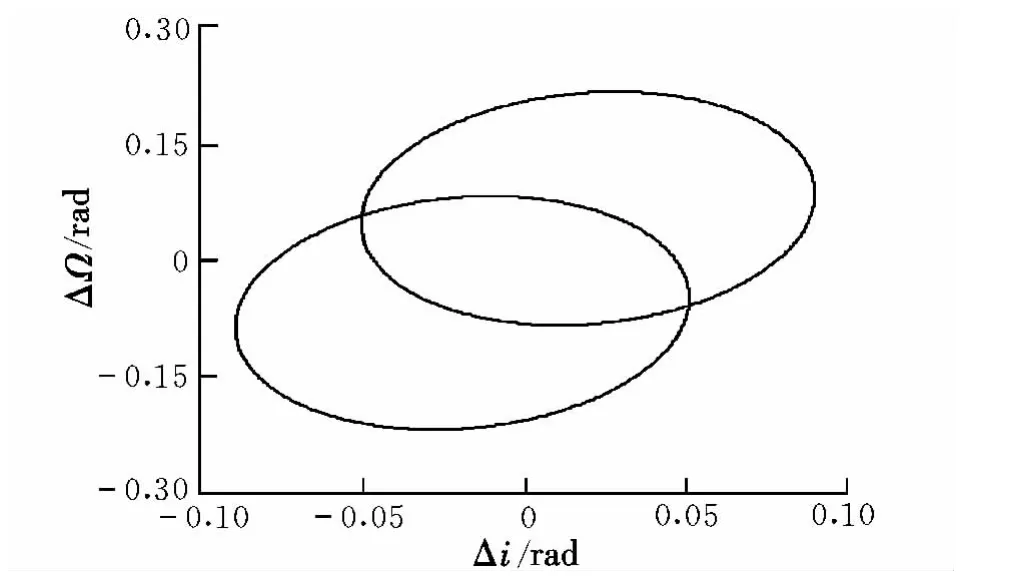
图6 在轨拦截器覆盖范围(垂直轨道面脉冲)Fig.6 Coverage area of orbit-interception(vertical impulse)

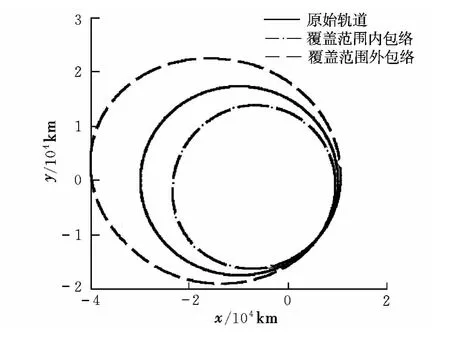
图7 在轨拦截器覆盖范围(Δi=0，ΔΩ=0)Fig.7 Coverage area of orbit-interception(Δi=0，ΔΩ =0)

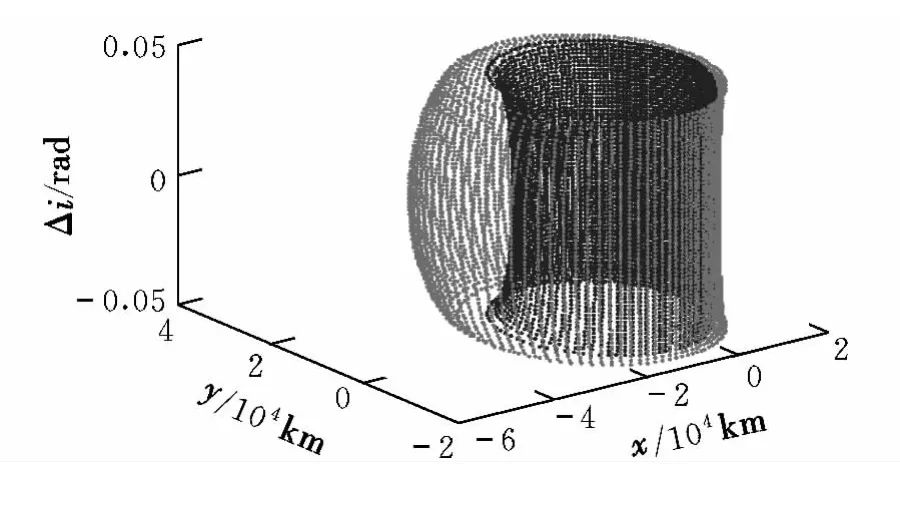
图8 在轨拦截器覆盖范围(ΔΩ=0)Fig.8 Coverage area of orbit-interception(ΔΩ =0)

5 结束语

作为动能型在轨拦截器实施机动及优化的前提，在给定最大变轨能力下的覆盖范围研究具有重要意义［12］。本文利用运动方程及高斯方程，分别研究了初始轨道为圆轨道及椭圆轨道在共面、垂直轨道面脉冲、任意方向脉冲作用等三种情况下在轨拦截器的覆盖范围。仿真表明，文中模型能够简捷有效地确定在轨拦截器的覆盖范围，为机动轨道设计与优化前提判断以及在轨拦截器的轨道设计提供技术支持。

［1］ Kamel O M，Soliman A S.On the optimization of the generalized coplanar Hohmann impulsive transfer adopting energy change concept［J］.Acta Astronautica，2005，56(4):431-438.

［2］ 李雪华，和兴锁，仲勤芳.单脉冲作用下卫星轨道的可达区域研究［J］.西北工业大学学报，2011，29(1):114-117.

［3］ 雪丹，李俊峰，宝音贺西.平面脉冲作用下卫星轨道的可达范围研究［J］.宇航学报，2009，30(1):88-92.

［4］ 雪丹，李俊峰.确定卫星可达范围的优化方法［J］.清华大学学报(自然科学版)，2009，49(11):1825-1855.

［5］ 雪丹，李俊峰，蒋方华.卫星在轨道平面内的可达范围研究［J］.力学学报，2010，42(2):337-342.

［6］ 常燕，周军.空间飞行器追踪区设计［J］.宇航学报，2006，27(6):1228-1232.

［7］ 陈茂良，周军，常燕.空间拦截攻击区和威胁区仿真研究［J］.航天控制，2009，27(1):41-48.

［8］ 周建华，徐波，冯全胜.轨道力学［M］.北京:科学出版社，2009:59-61.

［9］ 杨嘉墀，范剑峰，范秦鸿.航天器轨道动力学与控制［M］.北京:宇航出版社，1995:54-56.

［10］ Vinh N X，Gilbert E G，Howe R M，et al.Reachable domain for interception at hyperbolic speeds［J］.Acta Astronautica，1995，35(1):1-8.

［11］ Ranieri C L.Path-constrained trajectory optimization for proximity operations［R］.AIAA-2008-6275，2008.

［12］曹裕华，冯书兴，管清波.航天器军事应用建模与仿真［M］.北京:国防工业出版社，2010:1-8.