基于高斯过程的混凝土强度预测

林利森，肖义龙

（1.江西省安澜工程咨询有限公司，江西 南昌330001；2.河海大学设计研究院有限公司江西分公司，江西 南昌330006）

0 引言

随着我国经济的快速发展，工程建设项目中对混凝土的应用也将更加广泛。混凝土的抗压强度是混凝土的主要力学性质之一，在混凝土施工过程中经常会碰到浇筑各种配合比的大量混凝土而不知道其强度是否可以满足设计要求的问题。如何才能在短时间内得到所浇筑的混凝土预期的28 d强度是一个值得探究的科学问题，其对提高和控制施工质量具有重要的实际意义。

然而，混凝土强度的影响因素包括水泥的强度等级、水灰比、骨灰比、坍落度、水泥用量、粗骨料的最大尺寸、砂的细度模数、砂率等等，这些因素的共同作用决定了混凝土最终的强度。但是，这些影响因素与混凝土强度之间存在复杂的高维度非线性关系。多年来，为了探究各种因素之间的影响关系，国内外学者采用试验法、数值法、回归分析、随机模型等方法对混凝土强度的预测问题开展了大量的研究，并取得了一定的成效[1-2]。但由于该问题的高度复杂性，上述方法很难克服如数据有限，参数给不准的瓶颈问题。近年来，一些学者将神经网络（ANN）[3-4]、支持向量机（SVM）[5]等机器学习方法应用于混凝土强度的预测，取得了很好的研究成果，而由于这些方法本身还存在着一定的局限性，如：ANN对于小样本问题推广能力有限、SVM的核函数、核函数参数和损失函数难以确定等[6]。为此，探讨一种新的有效预测方法是很有必要的。

高斯过程（Gaussian Process，GP）是近年发展起来的一种新的机器学习方法，具有严格的统计学习理论基础，对处理高维数、小样本、非线性等复杂的问题具有很好的适应性[7～10]，现已成为机器学习领域的研究热点，并在许多领域都得到了成功的应用。

本文将高斯过程机器学习方法应用于混凝土强度预测，为混凝土强度的合理预测提供了一个有效的解决思路和方法。

1 高斯过程的原理简介

高斯过程是一种建立在高斯随机过程和贝叶斯学习理论基础上的机器学习方法。对于高斯过程机器学习原理存在两种不同的阐述方式，其一从函数空间观点[9-10]；其二从权重空间观点。本文从权重观点的角度进行阐述。

高斯过程回归模型实质上也是一种广义线性回归模型。首先假设有k个固定基函数的形式如｛φi（X）｝，则复杂的高维度非线性回归函数也可以通过基函数的线性组合表示，即：

根据贝叶斯原理，需要先设定一个先验参数权重w为满足均值为0，协方差矩阵为Σw的高斯分布，即：

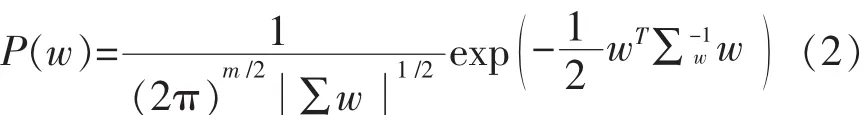
假设有m个观测值的训练样本集为D=｛（xi，ti）｜i=1，2，…，m｝，噪声ε服从相互独立且分布相同的高斯分布，其均值为零，方差为σ2n：

则含假设参数w的似然函数为：

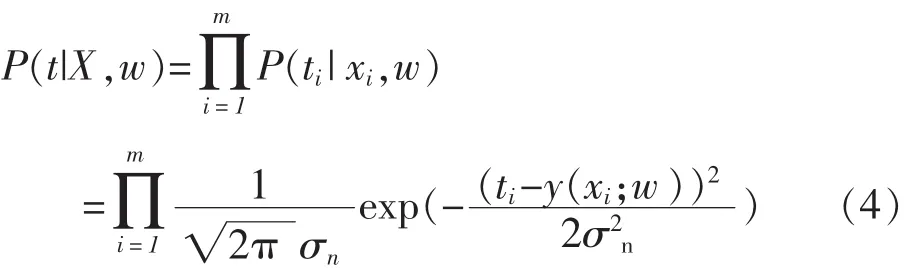
于是，基于权重w的后验分布为：

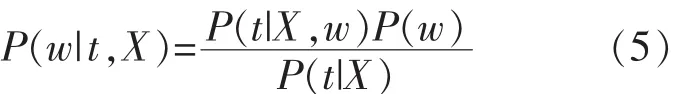
根据岭回归原理，权重w的最大后验概率的平均值wMAP可以通过求解下式的最小化获得：

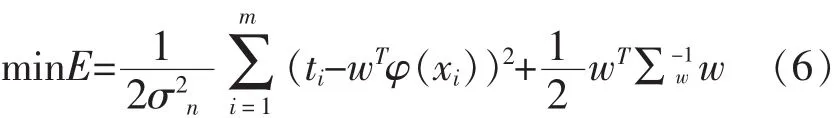
令β=1/σ2n，t=（t1，t2，…，tm）T，Φ表示为m×k的矩阵，即：

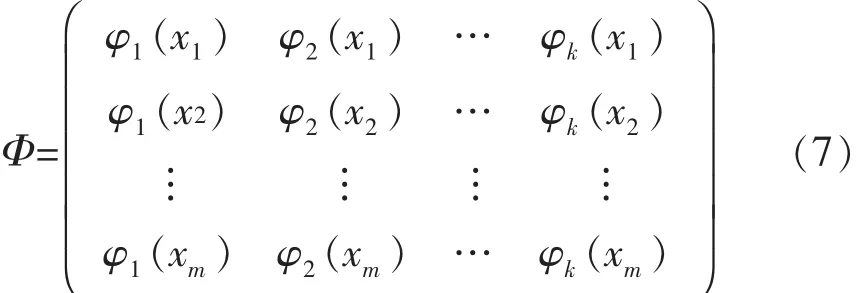
则式（6）也可以表示为：

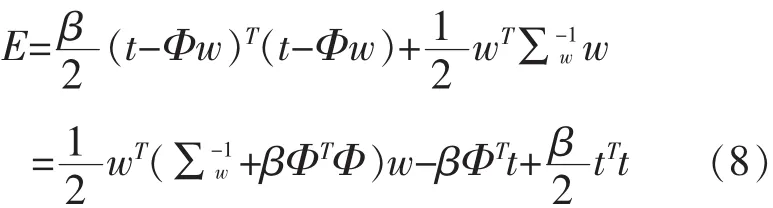
使式（8）最小化，则由E对权重w偏导数等于零（令A=βΦTΦ+Σ-1ww）得：

由上面的推导，获得了权重w的后验分布的具体形式，对测试样本x＊进行预测，则目标值的平均值表示为（设a=βA-1ΦTt）：

方差表示为：

在高斯过程机器学习中，常用的基函数形式为如下3种：

①平方指数协方差函数：

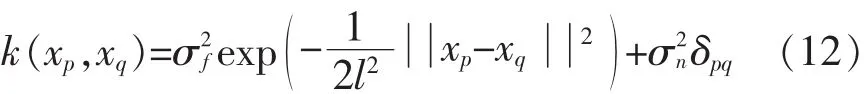
②当马特恩协方差函数中的参数v=3/2时，表达式形如：

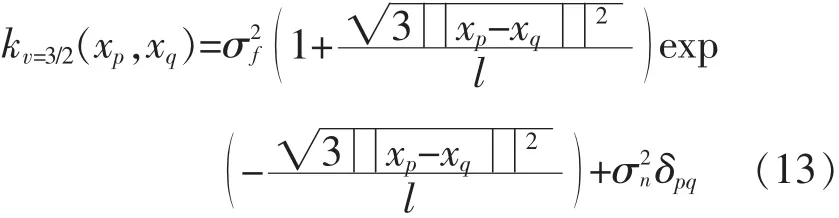
③线性协方差函数

式中最优超参数l、σf、σn即θ=（l，σf，σn），可通过极大似然法自适应获得。当其中xp=xj和xq=x＊时，则式（12）可表示为：

所以式（10）可写成：

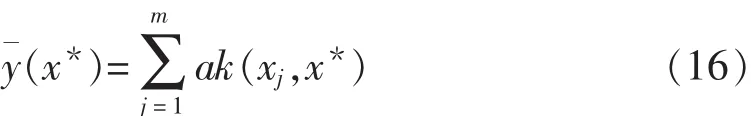
2 高斯过程的性能测试

为了更好地反映出高斯过程在处理小样本、非线性等复杂问题中具有很好的适应性的性能，在此引用一个经典的数学算例sinC函数进行分析[11～12]：

其中，学习样本由在x∈［-10，10］范围内等间距离散为10个随机变量x，然后对x对应的函数值y加上服从0.1倍的标准正态随机分布的噪音，最后分别采用四次多项式、ANN模型（BP神经网络）和GP模型对加噪后生成的10个学习样本（x，y）分别进行回归拟合分析（比较上述模型在学习样本被噪音腐蚀的情况下的拟合效果见图1）。

四次多项式函数形式为图1（a）；ANN回归时，其隐含层的神经元数目为5的拟合效果见图1（b）；神经元数目为15的拟合效果见图1（c）；采用GPR模型进行训练学习，自适应获取最优超参数对数后拟合效果见图 1（d）。

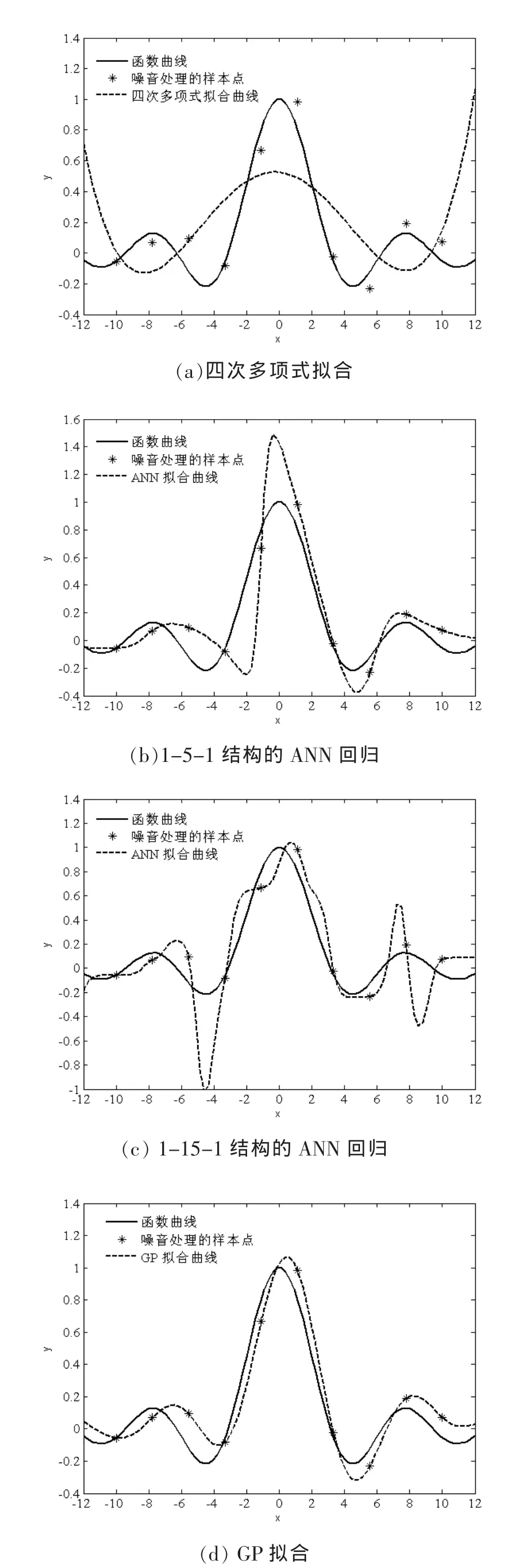
图1 不同模型的拟合效果比较

采用多项式拟合时，由于该函数的非线性较强，拟合曲线与真实函数的曲线相差甚远。即使增加学习样本的数量对其拟合效果亦无大的改进，其主要原因是多项式模型存在对高度非线性函数的拟合局限性问题。

采用ANN拟合时，其拟合效果较多项式拟合具有很大的改进，但也存在随着神经元数目的增加均会出现“过拟合”现象，而且拟合效果的精度与神经元数目存在很大的随机性（网络结构难以确定）。另外，值得指出的是，在算例的研究过程中发现，ANN的回归效果存在不稳定性，即使是同样的网络结构以及相同的参数，其回归效果也会存在较大的差异性。

采用GP拟合时，其拟合效果较ANN拟合精度具有一定的提高，同时不存在ANN的参数影响以及拟合效果不稳定性等问题。因为其最优超参数都是通过自适应获取，而且在算例的研究过程中发现，GP模型的参数一旦确定了，其最后的拟合效果就基本保持不变。因此，GP模型对于这种高度非线性函数的拟合效果更加令人满意。

3 工程实例研究

3.1 主要影响指标的确定

影响混凝土强度的因素众多，各因素之间又存在错综复杂的高度非线性关系。根据大量试验数据综合评定，最终选定了水泥强度、水泥用量、水灰比、骨灰比等9个指标作为主要影响因素。

3.2 高斯过程模型的建立步骤

（1）根据文献［3］中表2提供的33组混凝土试验数据（鉴于篇幅有限，不予以列出）建立学习样本（xi，yi）（i=1，2，…9），输入向量xi代表影响混凝土强度的 9个主要影响因素数值，输出标量yi代表混凝土强度。

（2）为了消除各主要影响因素之间存在的数量级差异，并提高GP的学习效果，有必要对样本数据进行如下的标准化处理：

（3）对学习样本进行学习，通过学习样本的对数似然（式（4））极大化获得最优的超参数。

（4）根据式（16）获得测试样本x＊（影响混凝土强度的9个主要因素组合）对应的混凝土强度的预测均值y＊。

根据上述步骤，采用MATLAB语言编制相应程序。

3.3 预测效果分析

采用文献［3］表5中的10个试验数据作为预测样本（见表 1）。

对学习样本进行学习，超参数对数初始值设为lnl=［-1，-1，-1，-1，-1，-1，-1］，lnσf=ln1.0，lnσn=ln0.01，以训练样本的极大似然为目标，采用共轭梯度优化算法搜索最优超参数。收敛标准设为最大迭代步数为300或迭代步之间的绝对目标值差值小于1×10-6。经过迭代得 到 最 优 超 参 数 值 为 ：l=［0.37，88.25，128.26，0.92，1.73，3.41，0.37，0.37，1.38］，σf=8.841，σn=0.49。

GP模型的预测结果见表2，从中可看出，GP模型预测样本的预测最大相对误差为2.06%。而文献［3］采用神经网络模型预测时，其精度明显不如GP。由此可见，两种模型相比较，GP模型对小样本问题的适应性较强，更简单实用，且精度高。

表1 混凝土试验数据实测值（预测样本）

表2 混凝土强度的实测值与预测值比较

4 结语

（1）传统方法难以处理混凝土强度与其影响因素之间存在高维度的复杂非线性关系，高斯过程机器学习方法能够很好的处理这种复杂关系。通过实例分析表明，混凝土强度的GP预测模型是可行的，且可以给出准确可靠的预测结果，对混凝土强度的预测具有很强的适用性。

（2）GP模型仅需有限个实测试验数据作为学习样本，就能建立相应的预测模型并预测出准确可靠的预测结果。然而，该方法预测精度的高低仍然会依赖于学习样本的质量好坏，如何获取高质量的学习样本将是该方法的下一步主要研究热点之一。

（3）高斯过程机器学习方法具有严格的统计理论基础、优良的学习和预测性能且实现容易等优点，现已成为当今机器学习领域的标准工具之一，在工程预测方面拥有广泛的应用前景。

［1］周慧麟，余永祯译.日本建筑学会，混凝土早期快速试验方法集（第一版）［M］.北京：中国建筑工业出版社，1991 年，6-11.

［2］吴中伟，康慧珍.高性能混凝土（第一版）［M］.北京：中国铁道出版社，1999，3-9.

［3］王继宗，倪鸿光，何锦云，等.混凝土强度预测和模拟的智能化方法［J］.土木工程学报，2003，36（10）：24-29.

［4］周 梅，刘 松，王海超，等.利用神经网络预测混凝土的抗压强度［J］.辽宁工程技术大学学报（自然科学版），1998，17（3）：275-277.

［5］武换娥，丁圣果，巩玉志，等.支持向量回归机在混凝土强度预测中的应用研究［J］.工业建筑，2007，37（增刊）： 991-995.

［6］肖义龙.基于高斯过程机器学习的结构可靠度分析方法研究［D］.广西大学， 2011，5-9.

［7］ M.Girolami and S.Rogers.Variational Bayesian multinomial probit regression with Gaussian process priors ［J］.Neural Computation，2006，18（8）：1790-1817.

［8］ R.B.Gramacy.tgp：An R package for Bayesian nonstationary， semiparametric nonlinear regression and design by treed Gaussian process models ［J］.Journal of Statistical Software， 2007，19 （19）：1-46.

［9］苏国韶，宋咏春，燕柳斌.岩体爆破效应预测的一种新方法［J］.岩石力学与工程学报，2007，26（增 1）：3509-3514.

［10］苏国韶，张 研，张小飞.高斯过程机器学习方法在地下水位预测中的应用［J］.中国农村水利水电， 2008（12）：48～50.

［11］邓万宇，郑庆华，陈 琳，等.神经网络极速学习方法研究［J］.计算机学报， 2010（2）：279～287.

［12］朱国强，刘士荣，俞金寿.支持向量机及其在函数逼近中的应用［J］.华东理工大学学报， 2002（5）：555-559.