由温度时序资料反演地下水流速的两种解析解及其比较

吴志伟，宋汉周

1.河海大学地球科学与工程学院，南京 210098

2.东北电力设计院，长春 130033

0 引言

地表水与地下水交换是水文学、水文地质学、环境科学、水资源管理等学科的研究重点之一，研究河床地表水与地下水交换的时空变化特征具有重要意义［1］。研究［2］发现，水作为热量的优良载体，在地表水与地下水交换过程中会携带能量变化的信息。利用热量在地质体中的传递规律，观测河床地下水温度场的时空分布，能够用来确定地表水与地下水之间的交换特征［3］。

早在20世纪60年代，Stallman［4］就介绍了利用地下水温度反演饱和多孔介质中垂向流流向和流速的方法——假设上部温度恒定，通过解析演算可以得到采用垂向温度曲线形态计算地下水流速的典型曲线法。此后，根据钻孔温度梯度的变化，采用Stallman模型计算地下水流速得到了广泛的应用［5］。但是Stallman模型假设浅部温度恒定，这显然是过于简化了，后续的研究开展了采用连续测温资料的“突变点”确定水文地质条件突变的方法［6］。而对于连续的温度波动资料，目前多数还是采用温度曲线形态定性地解释地下水流动，确定地表水与地下水交换的时空分布［7－9］，但是相关的定量研究还很少。渗流场与温度场耦合的数值模拟能有效地解决复杂的渗流传热问题［10］。数值模拟技术也在解释测温资料中得到应用，通过“试错法”拟合实测的钻孔温度曲线，得到地下水垂向流速［11］。

研究［2］发现，浅部地质体中的温度受大气温度影响，具有周期性波动特征，而不同深度处的温度波动是衰减的，且这种衰减特征与地下水活动密切相关；由此建立了采用温度时序资料计算垂向地下水流速的解析法。典型的解析模型有Hatch解［12］和Keery解［13］。 实 例 研 究［14－16］证 实 了 采 用 温 度 时 序曲线解析法能方便快捷地计算地下水垂向流速、确定地表水与地下水交换的时空分布特征。

上述解析模型假设垂向上能观测到温度的衰减，但若上、下2个测点的温度波动曲线一致，那么解析模型就不再适用；此外，在建立基本模型时，Keery解忽略了热弥散效应的影响，这必然引入一定的误差，已有研究尚未充分讨论Hatch解与Keery解的差异。

鉴于此，笔者基于解析模型的基本假设，通过算例研究了解析模型的适用性和局限性，讨论了Hatch解与Keery解的异同点；以期为有效地获取温度实测资料，并为由此解析地表水与地下水之间的交换而选用合适的求解方法提供依据。

1 温度资料反演地下水流速解析模型

1.1 基本原理

地表水体及其底部河床中渗透性介质的温度受气温影响，温度时序曲线具有日波动、季节波动等特征。河水与河床渗透性介质之间的热量交换受热对流作用的控制，即与地表水与地下水的交换过程密切相关。当地表水与地下水发生交换时，水流大小及方向对二者之间的能量传递过程具有显著影响。

如图1所示，在某测点垂向上可在不同位置（单井不同深度埋设探头）连续测量，以获得垂向上的温度波动差异。为了达到不同的研究目的，温度记录可以设置以时、天、月或年为时间间隔，得到观测点连续变化的温度波动资料。即，浅部测点（埋深为zs）温度时序曲线的振幅（As）必然大于深部测点（埋深为zd）的温度振幅（Ad），与此同时，二者存在相位滞后（Δφ）。

图1 温度时序资料确定地下水流速（v）方法示意图Fig.1 Sketch for determining seepage velocity（v）of streambed by temperature time－series records

如果没有地下水活动，河床浅部能观测到温度的日波动，再深的部位能观测到温度的季节波动或年波动。而在垂直向下水流作用的部位，表层水温的波动能够在岩土体中发生传导和对流，且渗流速度越大，热对流越强烈，在较深部位也能观测到温度波动，而且温度振幅衰减较慢，峰值延时较小；垂直向上的水流，对比于向下的水流作用，相同埋深点的温度振幅较小，峰值延时较大［17］。采用1D对流－传热模型，假设河水温度按正弦波动，得到河床渗透性介质的温度波动解析解；进一步得到利用同一测点不同深度处的温度时序曲线振幅比Ar（Ar＝As/Ad）和相位滞后Δφ来计算垂向地下水流速的解析法。

1.2 解析模型及2种解析解

1.2.1 1D瞬态对流－传热模型

在自然界中，河床地下水的垂向流动是普遍存在的，尤其是在河流的河谷中部。因此可以采用1D对流－传热模型来描述河床温度场。

首先对河床传热模型做如下简化：假设河床顶面水平、下部空间无限大、河床为均质各向同性的多孔介质，那么该半无限空间的1D瞬态热对流－传热方程［4］为

式中：T为深度z（m）处时刻t（s）的温度（℃）；ke为饱和多孔介质的等效热扩散系数（m2/s）；v为计算截面上的渗流流速（m/s，与z轴正方向相同为正，如图1所示，即向下的流速为正），基于典型单元体假设，v与地下水实际流速u存在关系式v＝neu，ne为有效孔隙度；ρw和cw分别为水的密度（kg/m3）和质量热容（J/（kg·℃））；ρ和c分别为饱和多孔介质的等效密度和等效质量热容。根据体积平均原理，ρ＝（1－ne）ρs＋neρw，c＝（1－ne）cs＋necw，ρs和cs分别为固体介质的密度和质量热容。

饱和多孔介质的等效热扩散系数ke定义为

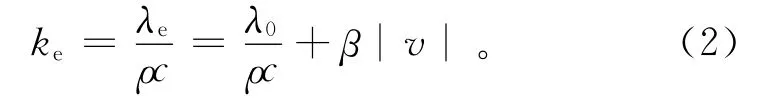
式中：λe为多孔介质的等效热传导系数（W/（m·℃））；λ0为基准热传导系数（W/（m·℃）），即没有地下水活动的热传导系数；β为热弥散系数（m）。对等效热扩散系数的定义考虑了水动力条件对介质传热的影响。

河水温度与气温的相关性密切，可以简化为按正弦波动的简单谐波信号：

式中：A为河水温度波动的振幅；P为温度波动周期；T0为上边界温度的非波动因子，约等于平均温度。在无穷远处的温度边界假定为地温不受波动因素及流体流动的影响。Hatch和Keery分别给出了上述模型的解析解。

1.2.2 1D瞬态对流－传热模型的解析解

1）Hatch解

Hatch［12］指出式（1）的解为

其中，

上述各式中的vT（温度前端运移速度）与地下水实际流速u之间的转换关系满足下式：

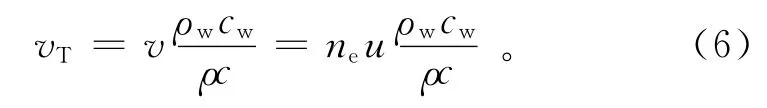
因河床渗透性介质满足均质各向同性假设，不同深度处的热物理参数相同，那么深处温度波动曲线与浅部温度波动曲线的振幅比Ar和相位滞后Δφ可以由式（4）得到：

式中，Δz为深处测点与浅部测点间的距离（m），Δz＝zd－zs。

由式（7）和式（8）分别得到温度前端运移速度vT，进而计算得到各计算时刻的渗流流速v。

2）Keery解

Keery［13］忽略地下水流动的热弥散效应，认为ke＝λ0/ρc，且直接采用渗流流速v计算，给出式（1）的解为

其中：

式（9）右侧即为某深度处温度曲线的波动因子，它受饱和多孔介质及流体的热物理参数、流速、表层温度波动等因素的影响。总体而言，受地质体的阻尼作用，当地下水流速恒定时，不同深度处温度曲线的振幅随着深度增加而衰减，峰值相位存在一定的滞后。同样由式（9）给出2个测点间的振幅比Ar和相位滞后Δφ，由此可得到由振幅比和相位滞后表示的地下水流速：

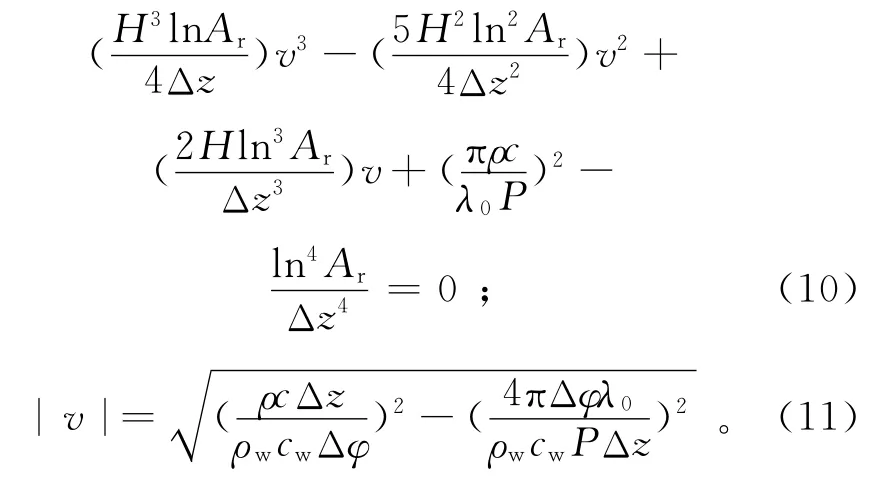
式中：H＝ρwcw/λ0。

1.3 工作方法

1.3.1 温度测量

目前常用的温度测量方法是将温度传感器布置在金属或PVC材质的护筒中，护筒管径不宜过大。若护筒为金属材质，可直接锤入河床；若护筒为PVC材质，可采用其他方法先成孔，然后埋设PVC管。护筒应保持竖直状态，且采取相应措施防止水流冲刷破坏。护筒与被测试位置的接触断面应设置滤孔和滤网，保证地下水能在护筒与岩土体中自由交换。测试护筒中地下水与测试点外围渗透性介质之间的热量平衡过程受护筒导热情况和滤网的渗透性影响。这种短暂的热平衡过程对温度时序资料测试成果有一定的影响，研究表明，护筒干扰对由振幅比计算地下水流速不会产生影响，而会给由相位滞后计算地下水流速带来误差［18］。

由于日周期波动信息观测起来较为经济，且波动振幅较大，是理想的温度时序资料，因此本文所述的温度时序资料解析模型以日周期信号为研究对象。一般情况下，浅部河床能观测到温度的日波动，传感器埋深越大，温度日波动特征越弱。传感器的埋置深度及埋设间距与地表水与地下水交换速率的大小有关：若地下水流速较大，则传感器需埋在较深的部位，传感器间距也应较大；若地下水流速较小，则传感器需埋在较浅的部位，传感器间距也应较小。

采用上述方法可以测得某一测点不同深度处的温度时序资料，采用前述解析模型能够计算该点的地下水流速在时间域上的变化。在平面上，可以布置多个测点，根据测点的势能差，采用Darcy定律，能够评价河床渗透性的空间差异。

1.3.2 温度时序资料滤波处理

实测的温度时序资料是多周期叠加的信号，为了应用前述解析模型，必须通过对测试数据进行滤波处理，得到按日周期波动的正弦信号。最简单的方法是通过快速傅里叶变换（FFT）的带通滤波，提取日周期信号。此外，可以采用更加适合处理周期性信号的动态谐波回归分析法（DHR法）对实测资料进行滤波处理。

1.3.3 地下水流速计算

深浅2个测点的温度实测资料经过滤波，得到按日波动的温度时序曲线，进而读取温度时序曲线的振幅和峰值相位。理论上，深部测点的温度振幅Ad总是小于等于浅部温度振幅As，0.0≤Ar≤1.0；相位滞后Δφ也是大于0的数。当岩土体热物理参数、任意2点的垂向距离、温度波动振幅比或相位差等参数已知时，采用 Hatch解（式（7）和式（8））或Keery解（式（10）及式（11））计算地下水流速。上述过程均可采用Matlab软件编写相应的程序来完成。式（7）及式（10）的根包含虚根，在实际应用过程中，取其实数根为地下水流速。

2 Hatch解与Keery解对比分析

2.1 计算参数

Hatch解中的等效热扩散系数ke是流速的函数，需采用迭代法求解；而Keery解忽略了热弥散效应的影响，计算比较简单。为了评价Keery解的这种处理是否有效，通过一个算例来分析该解析解由忽略热弥散效应所引入的误差。

参照溶质运移研究中的弥散度经验值，通常情况下，小尺度松散多孔介质的热弥散度值约为0.001～0.100m。因中砂最能代表河床渗透性介质，取中砂作为典型介质来评价上述两种解析解之间可能存在的差异，相关的热物理参数如表1所示。计算参数中的孔隙度0.37是中砂的典型值，介质的密度、质量热容和热导系数参照文献［19］，水的热物理参数参照相关手册［20］给出常温条件下的经验值。

表1 模型对比分析计算参数Table 1 Parameters for calculation

取测点间距为0.3m，相位差为π/10～π/5，振幅比为0.1～0.6，分别采用Keery解与Hatch解法计算地下水流速vk和vh。

2.2 对比分析结果

对比相同条件下两种解法的计算结果，得到Keery解不考虑热弥散系数（β）引入的误差如图2所示。因Hatch解考虑了热弥散效应，认为其计算值是相对精确的，图中Keery解的误差为（vk－vh）/vh。

当采用相位滞后法（图2a）计算时，对于1D瞬态热－流模型（式（1））的上述两种解法均不能确定地下水流向，得到的流速均为正值。图2a中：误差均为正值，说明Keery解析解计算得到的流速均大于Hatch解析解；当β≤0.01m时，两种解的计算结果很接近，β越大，Keery解带来的误差越大，当β＝0.10m时，两种解的计算结果最大偏差为12%；Δφ越小，两种解的计算结果差异越小。在本算例的假设条件下，解析解不适用于Δφ大于π/5的情况，因此对比分析未给出对应的情况。当β取值小于0.10 m时，采用Keery解所带来的误差是可以接受的。

图2 Keery解不考虑热弥散系数β引入的误差Fig.2 Error introduced by ignoring thermal diffusion coefficientβin Keery solution

当采用振幅比法（图2b）计算时，模型能够确定地下水流向，向下的流速为正，向上的流速为负。在本算例的假设条件下，计算得到的流速均为正值。图2b中：误差为负表示Keery解计算的流速小于Hatch解，说明当Ar＞0.3时，Keery解计算的流速偏小；当Ar＝0.3时，Keery解的相对误差最小。当β≤0.01m时，两种解析解的计算结果很接近，误差小于±6%；β越大，Keery解带来的误差越大；当β取值小于0.10m时，采用Keery解所带来的误差小于40%。当Keery解计算值大于Hatch解时：Ar越小，Kerry解析解所产生的误差越大；反之，Ar越大，Kerry解析解所产生的误差越小。

由以上分析可知：β越大，Keery解所产生的误差越大。当β＜0.01m时，Keery解忽略弥散效应的处理是可行的；当β＞0.10m，Keery解所产生的误差非常大。介质的热弥散度受介质空隙特征影响，并具有一定的尺度效应，可以结合流场介质特征确定是否可以忽略热弥散效应。Keery解与Hatch解除了本节所论述的差异外，二者的理论基础和计算方法是相同的。在后面的讨论中，只采用精度更高的Hatch解来进行分析。

3 模型解析解的适用性与局限性

3.1 解析解的适用性

采用温度时序资料解析模型计算地下水流速时，2个测点间必须存在振幅衰减和相位滞后。为了评价模型解析解的适用性，采用表1所列的典型介质的热物理参数计算振幅比及相位滞后与计算流速的关系，结果如图3所示。

图3 模型解析解确定地下水流速的适用性Fig.3 Limitations and applicability of the analytic model to determine seepage velocity in streambed

对于振幅比法：1）采用常规的测点距离（1.0m左右），振幅比法能有效评价流速在（－1.0～8.0）×10－5m/s的地下水活动。当地下水流速过小时，深处测点可能不存在温度的日波动；当地下水流速过大时，深浅2个测点的温度波动一致，同样无法采用该解析模型。2）振幅比法可以得到地下水流向，负值表示地下水补给地表水，只有2个测点的距离很小且振幅比较小时，才可以通过温度时序资料确定向上的地下水流动。3）测点距离越大，相同的振幅比所反映的地下水流速越大，即地下水流速较大时，需采用较大的测点距离。4）相同的测点距离，振幅比越大，深部温度波动振幅衰减越小，则地下水流速越大。5）当振幅比过大或过小时，振幅比的小幅变动代表了较大范围的流速，模型精度有所降低，因此需控制合理的测点间距，使得到的振幅比在合理范围内。

对于相位滞后法：1）采用常规的测点距离（1.0 m左右），相位滞后法能有效评价流速在（0.0～1.6）×10－4m/s的地下水活动，能计算的地下水流速的范围大于振幅比法。2）相位滞后法只能得到地下水流速，无法确定地下水流向。3）测点距离越大，相同的相位滞后所反映的地下水流速越大，对于大的地下水流速需采用大的测点距离。4）相同的测点距离，相位滞后越小，说明地下水流速越大。

3.2 解析解的优势

解析模型可以采用连续的温度观测资料评价研究时段内地表水与地下水交换速率的变化，操作较为简单。该模型特别适用于干旱地区或地下水集中开采地区的水资源研究，这些地区地表水与地下水的交换过程是动态变化的，通过地下水流速可以很容易地得到地表水与地下水水量交换的动态变化。

如果需要评价河床渗透性的空间分布，只需要测量测点水头差，根据Darcy定律即可计算测点间的平均渗透系数。这种评价是基于原位测试资料得到的，避免了取样扰动，显然评价结果更加可靠。

温度时序资料解析解的计算只需要2个测点的温度资料，温度测量既经济又可靠，使在研究区平面上布置多个测点成为可能。通过多点的测试成果，可以评价研究区河床渗透性介质渗透性的空间差异。

3.3 解析解的局限性

采用温度时序资料确定地下水与地表水交换的解析模型是基于1D半无限均质各向同性介质中热传导－对流模型得到的，只有当河床固相介质可以简化为均质、各向同性介质时才可以采用该模型。地质体的非均质性及各向异性对解析模型的精度会产生影响，如果浅部测点与深部测点的基本物理性质不一致，就无法得到采用振幅比或相位滞后计算地下水流速的解析解。

解析解只能用来计算地下水垂向流速，而河床地下水的多维流动是普遍存在的，多维流动对河水与河床的热量交换会产生一定的影响，也会给解析解带来一定的误差。因此在采用本文所述解析方法之前，需要初步查明河床渗透性介质的物理性质和地下水流场的基本特征，确定模型是否适用。

温度时序资料日波动信息的提取是决定模型精度的重要因素。采用合理的滤波方法提取有效的正弦信号，是处理温度实测资料的关键。温度时序资料曲线上常常含有突变点，这些突变点通常是由水动力条件或河水温度突变导致的。在滤波过程中，这些突变点可能会导致模型计算结果失真。

理论上采用竖向垂直剖面上任意2点的测温资料都可以计算2点之间的平均地下水流速。但是测点间距过大而地下水流速较小时，振幅比会过小，相位滞后会过大，影响模型计算，因此需要预估区内地下水流速以设置合理的测点间距。如果采用日波动信息计算地下水流速，测点的埋深不宜过大，因深部地质体中可能无法检测到日波动信息。如果需要评价河床的渗透性，可以同步测量测点间的水头差，由地下水流速和水力梯度计算介质渗透系数。而日波动信息适用于评价浅部河床的渗透性，季节波动或年波动适用于评价深部河床的渗透性。

4 工程实例

4.1 实测资料及其处理

为评价美国Russian河地表水资源与地下水资源的交换，索诺马水文局（Sonoma County Water Agency）以及美国地质调查局西区分部（Branch of Regional Research，Western Region ，USGS）在Russian河河床埋设了温度及水头传感器，连续观测河水及地下水的压力与温度变化［21］。此处选取日周期波动特征较为显著的某一测点的资料来分析。

首先将带滤网的PVC护筒打入河床渗透性介质，然后将温度探头悬挂在护筒中，分别测量0.00 m和0.30m处的水温。测试过程由数据记录仪控制、记录和存储，每15min记录一次。

采用动态谐波回归分析法（DHR法）［13］对实测资料进行滤波处理，设置基频为P＝12h，得到典型的按正弦简谐波波动的温度时序资料，如图4所示。DHR回归分析的计算值与实测值的拟合效果非常好，非周期因素具有若干“突变点”，反映水动力条件是不稳定的。采用数值方法提取了滤波之后的温度时序资料的振幅，即图中“基频振幅”所示，深部（0.30m）温度振幅与浅部（0.00m）温度振幅的比值为振幅比Ar。深浅2个测点滤波后的正弦曲线各极大值对应的相位滞后同样作为解析模型的输入变量，用于相位滞后法计算地下水流速。

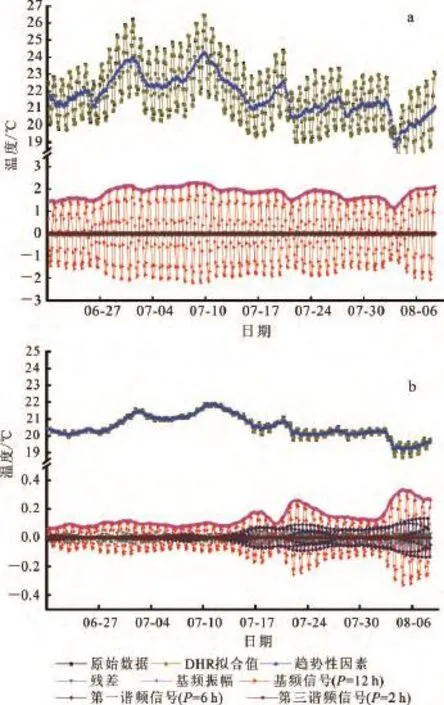
图4 测点温度时序资料DHR滤波分析成果Fig.4 Original and filtered temperature records

4.2 地表水与地下水交换速率

研究河段河床是未固结的砂砾石夹薄层淤泥或黏土。参照文献［19］，取岩土体的热物理参数如表1所示。采用2.2节所述之Hatch解析模型，得到观测时段内地表水与地下水交换速率的变化曲线，振幅比法的计算结果如图5所示，相位滞后法的计算结果如图6所示。研究时段内测点附近的地下水流速是动态波动的，具有如下特征：

1）振幅法与相位滞后法计算的地下水垂向流速差异不大，波动形态一致。当地下水补给河水时，相位滞后很小或超过π/2，无法采用解析模型计算，所以相位滞后法不能反映向上水流（图6）。而且相位滞后法只能反映地下水流速的大小，不能确定地下水流动方向，所以计算时间后段，振幅法确定的地下水流速存在负值，而相位滞后法无法确定正负。得到近似连续变化的河床地下水流速变化过程，对确定地表水与地下水的补排关系与补排量具有重要的应用价值。

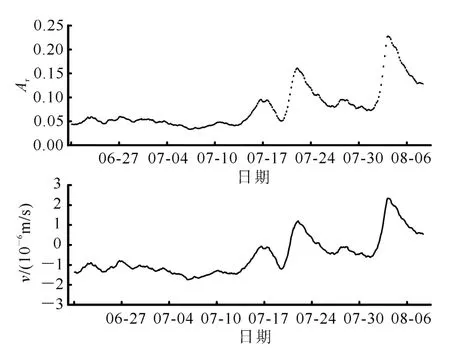
图5 振幅比法计算的地下水垂向流速Fig.5 GW－SW exchange velocity calculated from amplitude damping method

图6 相位滞后法计算的地下水垂向流速Fig.6 GW－SW exchange velocity calculated from phase lagging method

5 结语

1）对河床测温资料进行滤波处理，根据其振幅比和相位滞后可以计算地下水垂向流速，该方法可以方便快捷地评价地表水与地下水交换过程。

2）相对于Hatch解来说，Keery解忽略热弥散效应能引入较大的误差。当β＜0.01m时，Keery解忽略弥散效应的处理是可行的；当β＞0.10m时，Keery解所产生的误差非常大。

3）只有研究区能简化为均质多孔介质、地下水的1D垂向运动占主导地位时，才能采用解析法确定地下水流速；采用常规的测点距离（1.0m左右），振幅比法能有效评价流速在（－1.0～8.0）×10－5m/s的地下水活动，而相位滞后法能有效评价流速在（0.0～1.6）×10－4m/s的地下水活动。

4）后续的研究还需要进一步讨论多维流、岩土体非均质性对解析模型的影响。

2）7月17日之前是地下水补给河水，地下水流速较小且小幅波动，平均流速约为－1.0×10－6m/s。此时段河水水位较低，接受两岸地下水的补给。

3）7月17日—8月8日地下水流速总体上缓慢增大，震荡剧烈，大部分时段河水补给地下水，最大水流流速约为3.0×10－6m/s。地下水流速的动态变化曲线上存在2个峰值，分别是7月22日和8月4日，此时段河水受降雨影响，水位上升，地表水与地下水之间的水头差增大，地下水流速比较大。

上述分析表明，采用温度时序曲线解析法能够

（References）：

［1］王文科，杨泽元，程东会，等.面向生态的干旱半干旱地区区域地下水资源评价的方法体系［J］.吉林大学学报：地球科学版，2011，41（1）：137－144.Wang Wenke，Yang Zeyuan，Cheng Donghui，et al.Methods of Ecology－Oriented Groundwater Resource Assessment in Arid and Semi－Arid Area［J］.Journal of Jilin University：Earth Science Edition，2011，41（1）：137－144.

［2］方燕娜，廖资生，陈洪艳，等.吉林中部平原区地下水温动态变化影响因素的关联度分析［J］.吉林大学学报：地球科学版，2006，36（1）：66－72.Fang Yanna，Liao Zisheng，Chen Hongyan，et al.Correlativity Analysis of the Affect Factors on Groundwater Thermal Regime in the Plain Area of Central Jilin［J］.Journal of Jilin University：Earth Science Edition，2006，36（1）：66－72.

［3］Constantz J.Heat as a Tracer to Determine Streambed Water Exchanges［J/OL］.Water Resources Research，2008，44，W00D10，doi：10.1029/2008WR006996.

［4］Stallman R W.Steady One－Dimensional Fluid Flow in a Semi－Infinite Porous Medium with Sinusoidal Surface Temperature［J］.Journal of Geophysical Research，1965，70（12）：2821－2827.

［5］Anderson M P.Heat as a Ground Water Tracer［J］.Ground Water，2005，43（6）：951－968.

［6］Taniguchi M.Evaluation of Vertical Groundwater Fluxes and Thermal Properties of Aquifers Based on Transient Temperature－Depth Profiles［J］.Water Resources Research，1993，29（7）：2021－2026.

［7］Christian A，Kerst B，Ronny V，et al.A Simple Thermal Mapping Method for Seasonal Spatial Patterns of Groundwater－Surface Water Interaction［J］.Journal of Hydrology，2011，397（1/2）：93－104.

［8］Niswonger R G，Prudic D E，Fogg G E，et al.Method for Estimating Spatially Variable Seepage Loss and Hydraulic Conductivity in Intermittent and Ephemeral Streams［J/OL］.Water Resources Research，2008，44： W05418，doi：10.1029/2007WR006626.

［9］Brewster C J.Delineating and Quantifying Groundwater Discharge Zones Using Streambed Temperatures［J］.Ground Water，2004，42（2）：243－257.

［10］吴志伟，宋汉周.坝址温度场与变物性渗流场全耦合分析［J］.水利学报，2010，41（6）：703－710.Wu Zhiwei，Song Hanzhou.Fully－Coupled Analysis of Temperature Field and Variable Properties Seepage Field Around Dam－Site［J］.Journal of Hydraulic Engineering，2010，41（6）：703－710.

［11］Su G W，Jasperse J，Seymour D，et al.Estimation of Hydraulic Conductivity in an Alluvial System Using Temperatures［J］.Ground Water，2004，42（6）：890－901.

［12］Hatch C E，Fisher A T，Revenaugh J S，et al.Quantifying Surface Water－Groundwater Interactions Using Time Series Analysis of Streambed Thermal Records：Method Development［J］.Water Resources Research，2006，42（10）：W10410.

［13］Keery J，Binley A，Crook N，et al.Temporal and Spatial Variability of Groundwater－Surface Water Fluxes：Development and Application of an Analytical Method Using Temperature Time Series［J］.Journal of Hydrology，2007，336（1/2）：1－16.

［14］Hatch C E，Fisher A T，Ruehl C R，et al.Spatial and Temporal Variations in Streambed Hydraulic Conductivity Quantified with Time－Series Thermal Methods［J］.Journal of Hydrology，2010，389（3/4）：276－288.

［15］Cordon R P，Lautz L K，Briggs M A，et al.Automated Calculation of Vertical Pore－Water Flux from Field Temperature Time Series Using the VFLUX Method and Computer Program［J］.Journal of Hydrology，2012，420/421：142－158.

［16］Lautz L K.Observing Temporal Patterns of Vertical Flux Through Streambed Sediments Using Time－Series Analysis of Temperature Records［J］.Journal of Hydrology，2012，464/465：199－215.

［17］吴志伟，宋汉周.浅层地温场中热对流数值模拟［J］.岩土力学，2010，32（4）：1303－1308.Wu Zhiwei，Song Hanzhou.Numerical Simulation of Thermal Convection in Shallow Ground Temperature Field［J］.Rock and Soil Mechanics，2010，32（4）：1303－1308.

［18］Cardenas M B.Thermal Skin Effect of Pipes in Streambeds and Its Implications on Groundwater Flux Estimation Using Diurnal Temperature Signals［J/OL］.Water Resources Research，2010，12：W03536，doi：10.1029/2009WR008528.

［19］Healy R W，Ronan A D.Documentation of Computer Program VS2DH for Simulation of Energy Transport in Variably Saturated Porous Media［R］.Denver：US Geological Survey Information Center，1996.

［20］Weast R C.Handbook of Chemistry and Physics［M］.Boca Raton：Chemistry Rubra Pun Co Press，1982：261－263.

［21］Marisa H C，Hatch C E.Water Temperature，Stream Flow and Ground－Water Elevation in and Adjacent to the Russian River Between Hopland and Guerneville，CA，from 1998－2002［R］.Menlo Park：US Geological Survey Information Center，2003.