平面四参数转换在水利工程坐标系建立中的应用
2014-12-25许俊杰
许俊杰
(山西省水利水电勘测设计研究院 山西太原 030024)
0 引言
在工程控制网观测数据归算到国家坐标系统时,实测的边长要进行各项改正,改变各边的真实长度,从而引起长度变形,不利于大比例尺地形图测绘和施工放样[1]。近些年,在我国的水利工程中,施工区域有着狭窄、跨区长的特点,设计线路由于经过一些地表起伏较大的区域,会产生不同的长度变形。为满足水利工程建设的精度要求,控制测量时需选择合适的坐标系统,尤其需要采取有效的方法控制长度变形。坐标系统选择和长度变形控制对线路中线定桩、隧洞贯通、桥梁及渡槽的架设以及其他部分施工的精确度有着直接的影响[2]。
为避免重复测绘,使测量成果更有效利用,一般采用国家统一的3°带高斯平面直角坐标系。这样就使得工程测量控制网同国家测量系统相联系,利于测量成果相互转换利用。通过深入分析长度综合变形产生的原因,本文提出了在抵偿高程面上应用相似四参数模型经过“二次坐标变换”控制长度综合变形,使整个测区变形尽可能分布均匀[3]。
1 长度综合变形的控制
为了有效地控制投影长度变形,通常需要建立工程独立坐标系,将实测数据在独立坐标系下进行处理,另外,还需要将独立坐标系下的成果转换到国家坐标系下,以便为后续工程建设服务[4]。
1.1 长度综合变形值
由大地测量理论可知,将实地测量的真实长度投影到高斯平面上,需要加上两项改正,即实量边长归算至参考椭球面上的变形,与椭球面上的边长归算至高斯投影面上的变形之和,即为长度综合变形量,不同投影面上的同一距离近似相等,长度综合变形的计算公式为[5]

式中:Hm—长度所在高程面对于椭球面的高差;
s—实测水平距离;
R—测区中点的平均曲率半径;
ym—距离的两端点横坐标的均值。
式(1)中右边的第一项为实测距离到参考椭球面的改化,第二项为参考椭球面到高斯投影面的改正。由此可以得出,地面上的一段实测距离,在经过两次改正后,改变了真实长度。
为了便于计算,可以将椭球视为圆球,取其平均半径R=6371km,又取将式(1)写成相对变形的形式,则为[5]

式中,y表示测区中心的横坐标 (自然值),H表示测区平均高程,y与H均以km作单位。利用式(2)可以计算出测区所在坐标系统的长度综合变形的相对值。
工程控制网是工程施工测量和大比例尺测图的基础,就其实用性而言“长度综合变形愈小愈好”。通常情况下,工程控制网的坐标系统要求遵循长度综合变形不超过2.5cm/km(相对变形为1:40000)的原则[6],与四等平面控制网边长的精度相适应。
1.2 相似四参数坐标转换
工程坐标系的建立有多种方法,具体选择什么方法,需要综合多种因素作出选择,其最终的目的是减弱长度综合变形的大小。
长度综合变形在距离中央子午线近的区域越小,反之越大。在测区面积较大的情况下,边缘长度综合变形仍然不能满足高精度施工放样要求。总之,长度综合变形不够“均匀”,为了从整体上进一步控制长度综合变形,本文应用四参数转换模型进行“二次变换”来控制长度综合变形。
将一个平面坐标系下的坐标转换到另一个平面坐标系下可采用平面相似四参数模型,式(3)是平面相似四参数转换模型[7]
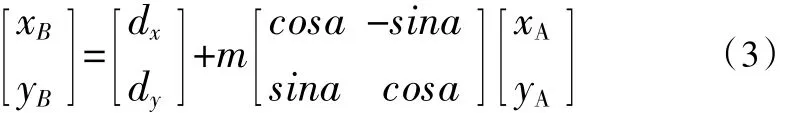
式中,dx,dy为平移参数,α为旋转参数,m为尺度参数。xB,yB为目标坐标系下的平面直角坐标,xA,yA为原坐标系下平面直角坐标。
为了求解四个参数至少需要2个重合点,将式(3)写观测方程的形式

经最小二乘求得四个参数dx,dy,u,w,再由式(5)求转换角a,进一步求解出尺度参数m。

1.3 二次坐标变换法
为了从整体上控制长度综合变形,选用四参数模型进行“二次坐标变换”的方法从全局出发进行坐标变换。二次变换的计算步骤:
(1)首先由测区的GPS控制点或已有的国家等级控制点计算抵偿高程面,计算公式

式中,ym是测区中心的横坐标,100 km,Hm和H抵,m。
(2)确定抵偿面位置后,在测区中均匀选取2个以上的控制点,将接近测区中心的一个作为“原点”,使它保持国家统一坐标值(x0,y0)不变,而把所选择的其他控制点坐标(x,y)换算到相应的抵偿高程面上。换算公式为
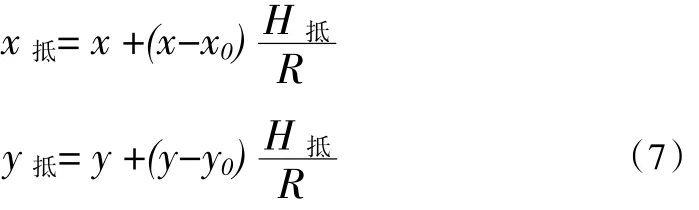
(3)在步骤(2)中选择的控制点既有国家控制点坐标值,也有抵偿面上的坐标值,这些点作为重合点应用四参数模型求转换参数。
(4)将测区内所有控制点利用已计算出的四参数转换到抵偿高程面上。具体的计算流程见图1。
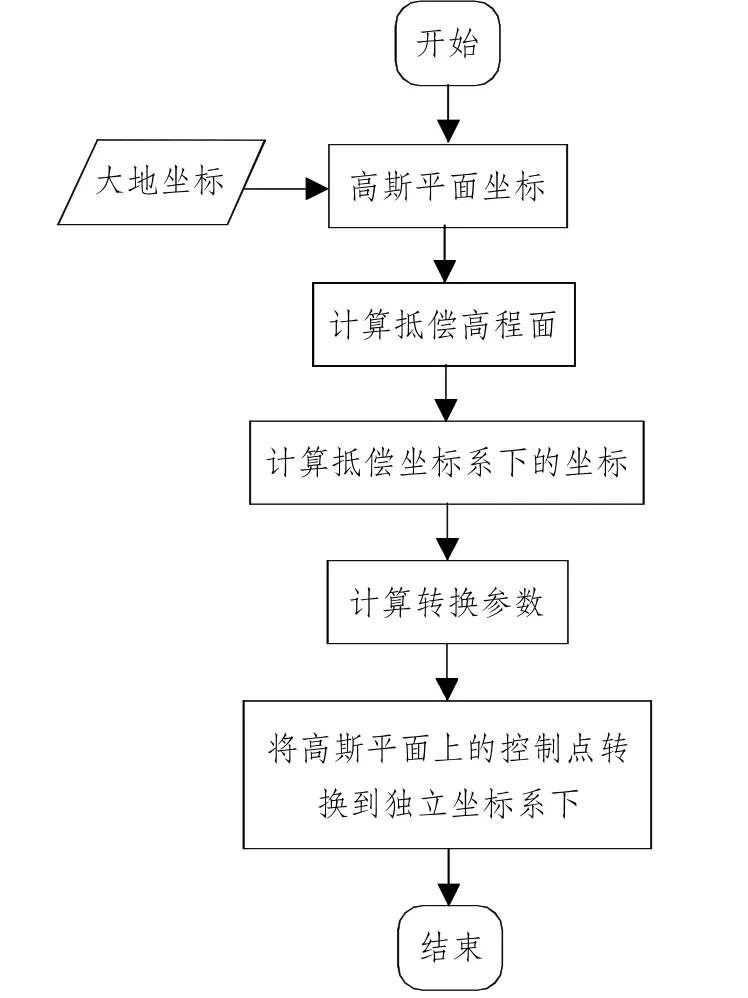
图1二次变换计算流程
2 实验分析
以某大水网输水工程坐标系统转换为例,用GPS实测了11个控制点,分布见图2。测区平均高为1300 m,中央子午线为111°,将GPS大地坐标转换为3°带高斯平面坐标,结果为表1(表中数据已经过处理)。
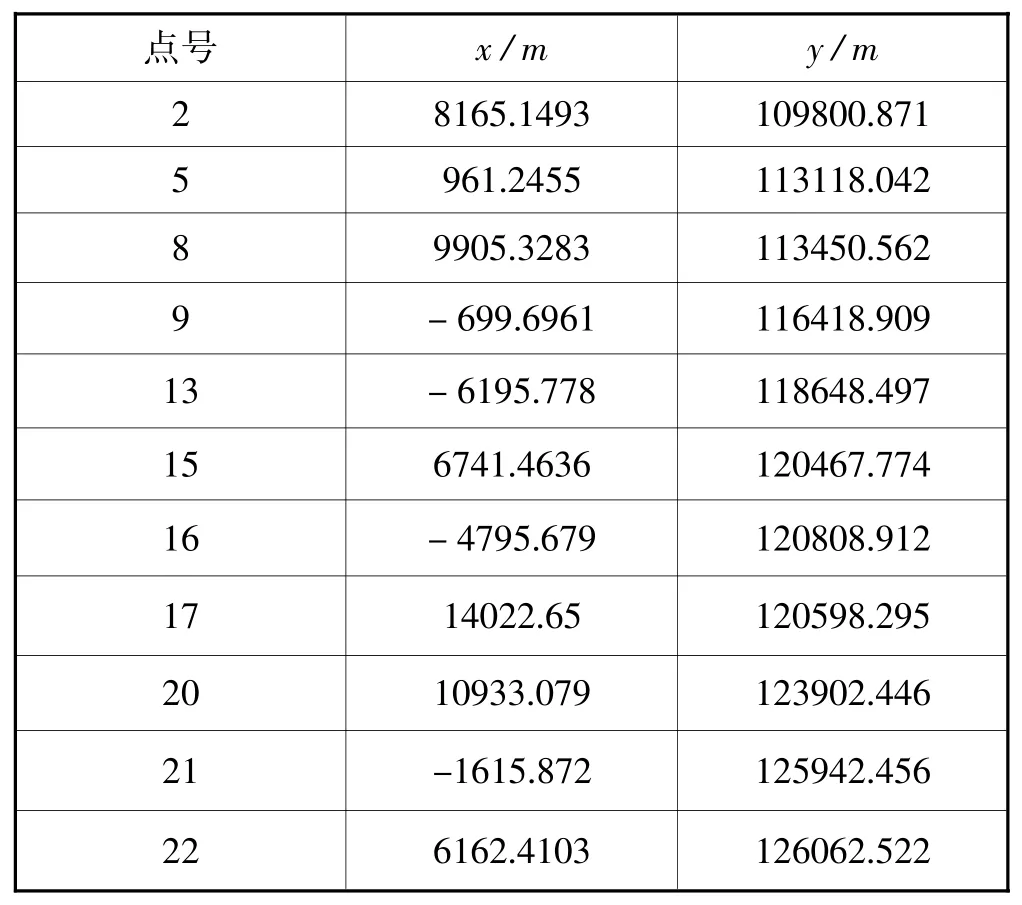
表1 高斯平面坐标

图2 控制点分布图
测区中心的横坐标y=120 km,由式(6)计算得抵偿高程面为H抵=170 m。由图2可知,15号点基本位于测区中心,因此选15号点作为原点,保持它在高斯平面上的坐标值(x0,y0)不变,选择其中4个点(2、17、13、22)按式(7)计算各点在抵偿高程面上的坐标,计算结果见表2。
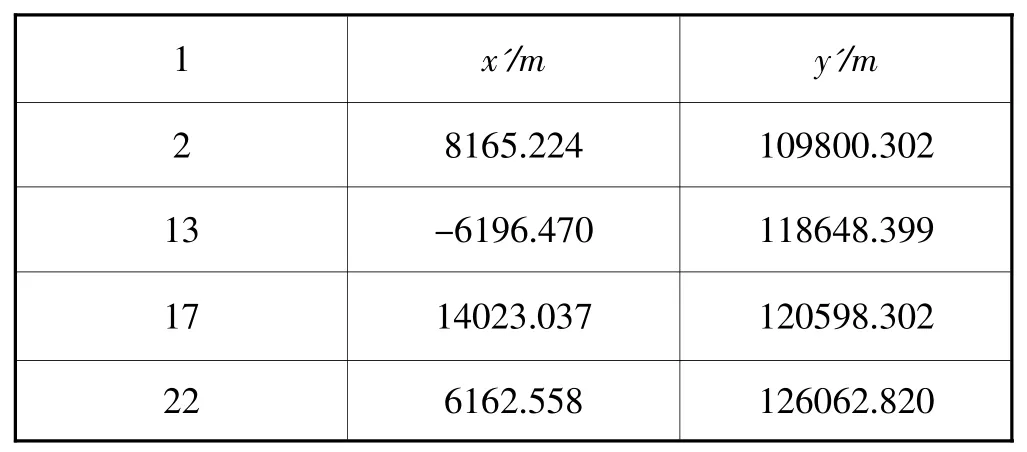
表2 抵偿高程面上的坐标
在高斯平面坐标系和具有抵偿投影面的高斯正形投影平面直角坐标系中有4个重合点,计算坐标转换四参数(dx=-0.576m,dy=-3.231m,a=-0.76′,m=1.000027)。然后利用四参数模型转换其他点坐标上,结果见表3。
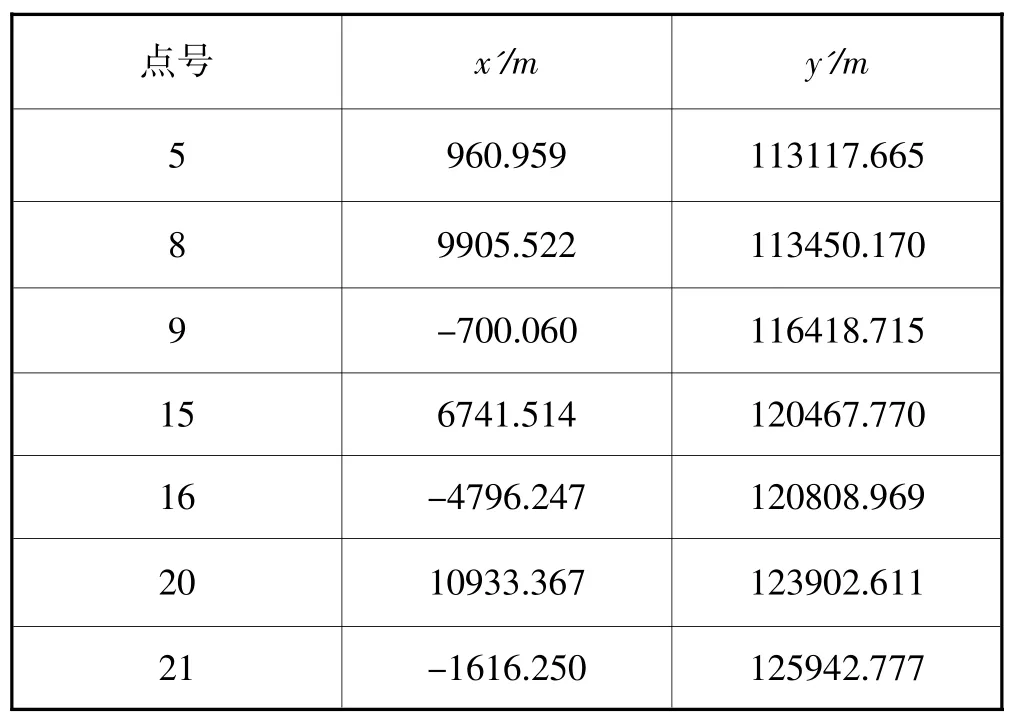
表3 二次变换后坐标
为了验证“二次变换”的可行性,实测了测区边缘的两条边长进行验证,即已知2号点到5号点、13号点到16号点两条边的实测长度,分别计算其在经过二次变换后的抵偿高程面上的长度S1和高斯平面坐标系下的长度S2及相对变形,计算结果如表4。从表中的结果可以看出,经过二次变换后的坐标反算距离与实测距离接近,其长度综合变形小于2.5cm/km的要求。

表4 长度变形对比
3 结论
通过变更投影面来抵偿长度综合变形将测区内的控制点成果投影到抵偿面上,该方法换算简便、概念直观,而且所得新坐标与原国家坐标系坐标十分接近,利于测区内外间的联系。然而由于受地形、测区控制点分布及测区面积大小的影响,测区内的长度综合变形并不“均匀”,在边界上长度变形甚至超限。为解决这一问题,本文提出了利用平面四参数转换模型进行坐标的二次变换,达到从整体上控制长度综合变形的目的。
四参数法的优点在于不需要提供当地椭球和地图通用模型就可利用最少的点计算出转换参数。而且在利用这种方法进行平面点位转换时,点位高程和平面坐标的转换分开进行,高程误差不会传播给平面坐标,而平面位置的误差也不会影响到高程的转换精度[8]。另外,为了实现一测多用,应用四参数模型将独立坐标系下的成果转换到国家坐标系中。
[1]陈顺宝,任建春,亓月,等.抵偿任意带高斯投影平面坐标系选择的研究[J].测绘通报,2005(07):21-23.
[2]陆鹏程,李全海,朱丹.铁路独立坐标系的建立及坐标转换[J].测绘科学,2012,37(1):20-22.
[3]刘传志.山区公路测设长度综合变形问题的研究[J].测绘工程,2007,16(4):60-62.
[4]秦菊芳,胡有云,等.高等级公路测设综合变形问题的研究[J].测绘通报,2002(9):28-30.
[5]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2006.
[6]中国有色金属工业协会.GB50026—2007工程测量规范[S].北京:中国计划出版社,2008.
[7]王建民,王发祥.高速铁路平面控制网测量数据处理方法研究[J].工程勘察,2011,39(7):86-89.
[8]杨国清,张予东.平面控制网四参数法坐标转换与残差内插[J].测绘通报,2010(11):48-50.
