基于Fluent的灌区明渠平板闸门三维流场数值模拟

2014-12-25徐宏海

山西水利科技 2014年2期

王勇徐宏海张菊

（北方工业大学机电工程学院北京100144）

明渠流动是对具有自由表面的水流在有限尺度的固体边界约束下的流动的一种概化[1]，包含大量的天然河流、水库和人工渠道。前人对明渠水流进行了大量的研究，为工程应用提供了重要指导[2][3]。这些研究主要着眼于具有高水头、大流量等特点的流动，针对广大灌区的小型明渠中水位传感器安放位置的研究较少。在水资源日趋紧张的形势下，推广使用具有计量功能的平板闸门，实现定量供水灌溉，是提高灌区水资源利用率的关键技术之一。研究灌区明渠平板闸门的流动特性，是提高闸门计量精度的前提。

计算机技术的发展使得基于计算流体动力学（CFD）的数值模拟技术在很大程度上替代了经典流体力学中的一些近似算法和图解法，使其在流体计算领域得到空前的应用。Fluent是目前比较流行的CFD软件，接口强大，方便导入多种格式的几何模型，包含丰富的物理模型、先进的数值方法及强大的前后处理功能。因此，本文将采用Fluent软件对矩形渠平板闸门闸孔出流的流动特性进行数值模拟。

1 VOF模型及控制方程

自由液面的数值模拟常用VOF[4]（Volume of Fluid）法。VOF法由C.W.Hirt和B.D.Nichols于1981年提出，该方法通过求解一套动量方程和连续方程模拟两种或多种流体的运动，追踪每种流体所占的体积，以此来确定自由液面。由于精度高、稳定性好、网格划分灵活，VOF模型已广泛用于明渠、水坝、阀[5]、泵[6]等领域的研究。

以水气二相流为例，VOF模型的核心思想是：定义函数qw（x,y,z,t）和qa（x,y,z,t）分别代表单元内水和空气的体积分数。在每个单元中,水和空气的体积分数之和为1,即：

若 qw=1，表明该单元充满水；若qw=0，则该单元充满空气；若0＜qw＜1，则该单元部分是水、部分是空气，该单元就必然包含自由液面。以液相的水为例，其体积函数控制方程为：

其中，t为时间，ui和xi分别为速度和坐标的分量，且{ui=u,v,w}，{xi=x,y,z},表明体积分数是时间和空间的函数，故VOF方法对流场的计算需要用非定常模型求解。

紊流模型采用标准k-ε紊流模型，引入VOF模型的k-ε方程如下：

连续性方程：

动量方程：

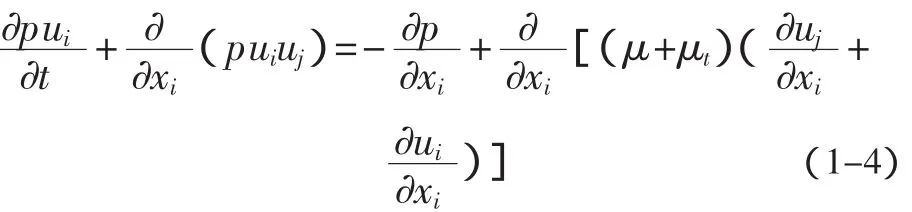
k方程：

ε方程：

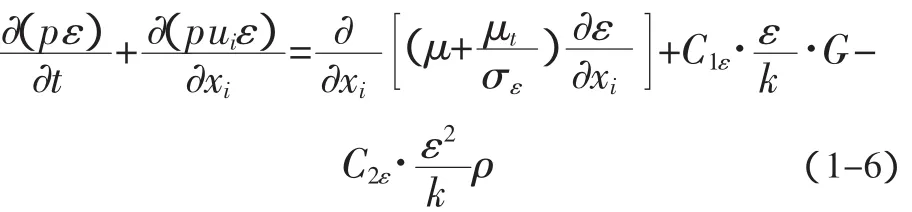
式中：ρ——按体积分数加权平均的密度；

μ——分子粘性系数；

P——修正压力；

σk、σε——紊流普朗特数；

G——由平均速度梯度引起的紊动能；

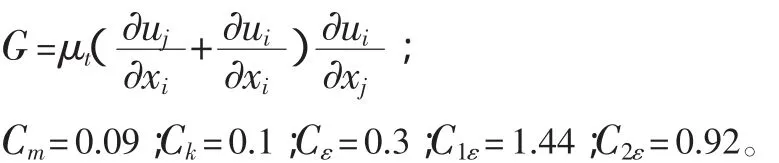
2 几何建模及网格划分

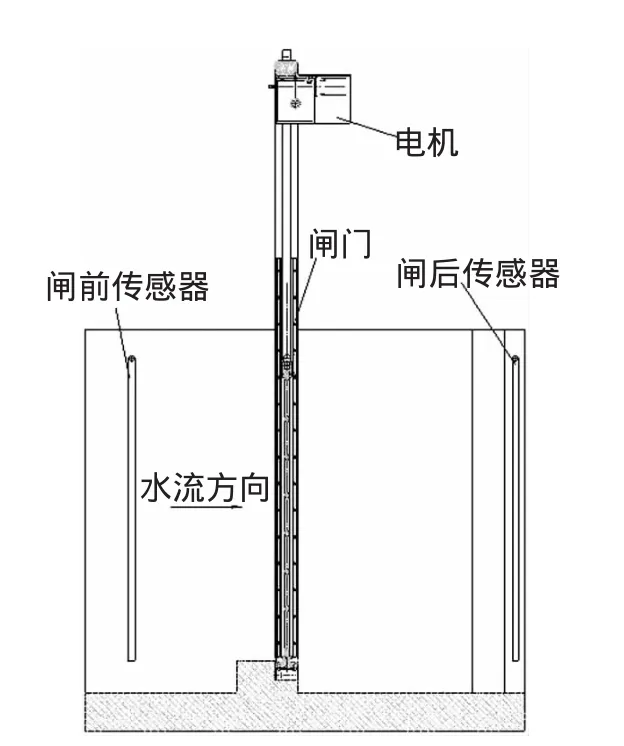
图1 闸门安装示意图

闸门安装示意图如图1所示，闸前、闸后传感器为压力传感器，用于测量闸门前、后的实时水位。

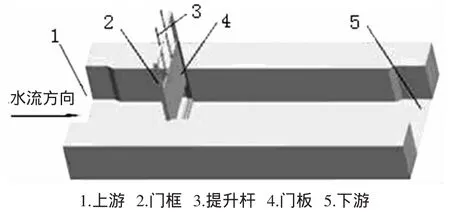
图2 明渠及闸门三维模型

水位传感器安放位置距离闸门较近时，受水流流态不稳定的影响常出现测量不准的情况，因此本文在建模时扩大了闸门前后扩口与闸门的距离来探讨合理的安放位置。矩形明渠及平板闸门三维模型如图2所示。明渠宽度为2.4m,闸门宽度为2m，为了便于安装，在闸门前后适当区域内渠道宽度收缩至2m；整个计算域长度为9.2m。

为了便于计算，对模型进行一些简化处理,由于闸门行程为1.2m，故上游计算域高为1.2m，初步对该问题仿真时发现下游水位不高于1m，因此下游计算域的高设为1m；由于明渠沿中心面严格对称，内部流场也因此呈对称分布，所以只需对中心面一侧做数值模拟即可得到整个流场的流态。简化后计算域尺寸为1.2m×1.2m×9.2m，纵向剖面如图3所示。

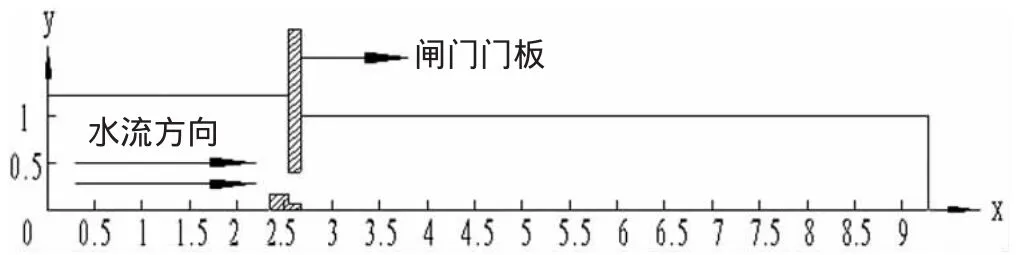
图3 计算域纵向剖面图

利用Gambit软件将几何模型划分为六面体网格,并在闸孔前后壁面附近适当范围加密网格，得到的网格文件共有189870个单元，网格的Skewness值最大为0.4，表明网格质量良好。

3 边界条件及求解方法

该型闸门目前用于山西省某引黄灌溉区的农渠，有1或2台水泵从水库向明渠上游供水，工作时根据需要选择1或2台水泵，水泵流量已知。由水泵流量和入口断面面积可得到水流进口断面平均流速(如公式3-1)，因此水流进口可采用速度进口；空气进口采用压力进口，下游出口采用压力出口，压力设为0，参考压力为一个大气压。湍流动能k和湍流耗散率ε的初始值分别按公式3-2、3-3计算[7]；固壁面采用无滑移不可入壁面，法向和切向速度均为0，忽略壁面糙度的影响；近壁区采用标准壁面函数法处理。

式中：Q—水泵流量；W—明渠宽度；h—上游水深；v—入口断面平均流速；I—湍流强度，I=0.16Re0.125，Re—雷诺数；l—特征尺度,l=0.07L，L—水力直径。

数值计算采用有限体积法离散微分方程组；对流项采用二阶迎风格式；压力速度耦合求解采用PISO算法，时间上采用隐式解法。

为提高灌溉效率，闸门实际工作时常使上游避免出现较低水位（即初始条件下的计算域进口水位），同时为降低闸门受力，需避免闸门开度过小，以此为原则并结合初步的仿真结果进行工况设计。初始条件中闸门开度（e）、计算域进口水位（h），进口速度（v）按表1给出。

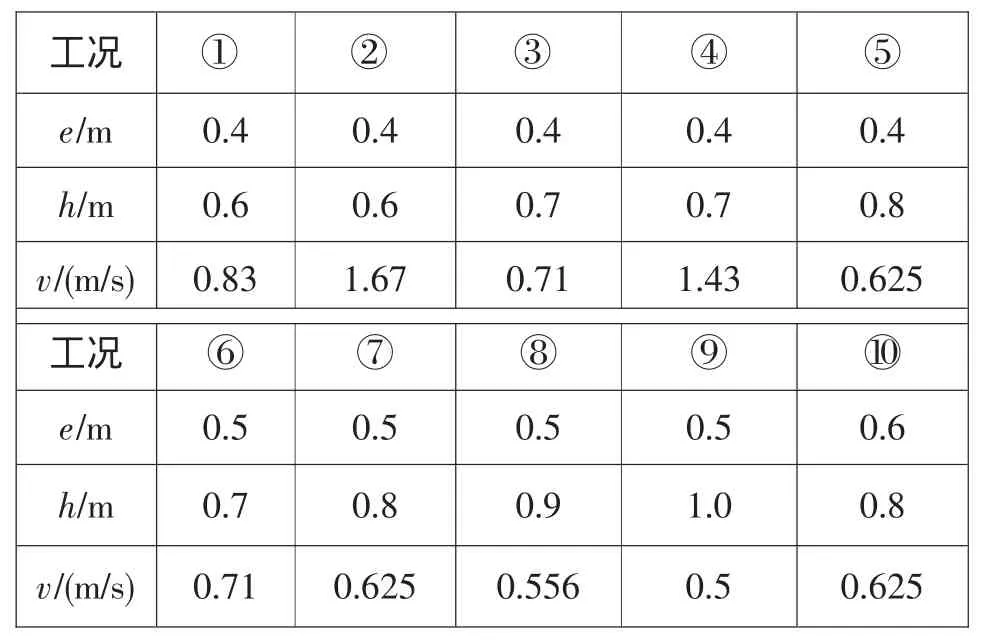
表1 仿真工况设计

4 结果分析

1）水位

（1）当闸门开度和计算域进口的初始水位一定，进口流量不同时，比较在工况①、②、③、④条件下其水位如图4、5所示，从计算域沿程3.5m处开始，水位已趋于平稳，工况①、②的水位差约0.054m，工况③、④的水位差约0.043m。当闸门开度和进口流量一定，计算域进口的初始水位不同时，比较工况①、③发现计算稳定后的闸前水位略低于初始水位，表明此时闸门并未对闸孔出流造成限制；工况②、④条件下闸前水位达到1.1m，水在闸前0.3m处出现了翻滚，水位升高至1.25m，表明闸门未限制出流。

图4 工况①、②条件下的水位

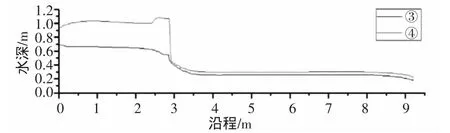
图5 工况③、④条件下的水位

（2）当计算域进口的初始水位和进口流量一定，闸门开度不同时，比较在工况⑤、⑦、⑩条件下水位如图6所示。稳定后的闸前水位均小于初始水位0.8m，同样表明闸门未限制出流，下游水位基本一致，三个工况的水位差在0.001m左右。

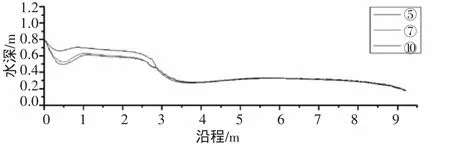
图6 工况⑤、⑦、⑩条件下的水位

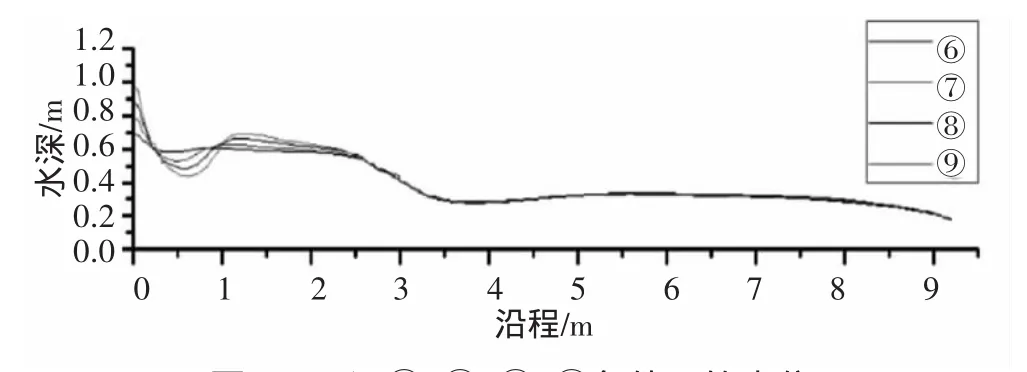
图7 工况⑥、⑦、⑧、⑨条件下的水位

（3）当闸门开度和进口流量一定，计算域进口的初始水位不同时，比较在工况⑥、⑦、⑧、⑨条件下水位如图7所示。各工况稳定后的闸前水位均小于其初始水位，表明闸门未限制出流，下游水位基本一致，相差在0.006m以内。

对比以上工况的水位，发现单、双泵供水时均在闸后约1.5m范围内出现明显的湍流，当双泵供水时上游水位较高，说明闸门开度已成为限制出流的因素，并且闸前易出现翻滚，为减小闸门门板受力应适当增大开度，闸后水位较单泵供水时高，但水流相对平稳；单泵供水时闸孔出流通畅，除闸后1.5m区域外，其余流场均很平稳，符合平板闸门在灌区明渠实际工作的情况，说明本次数值模拟采用的方法是合理的。

2）压力分布

笔者发现各工况条件下，明渠底部压力分布基本一致，只以工况①做分析，如图8所示。明渠上游收缩断面处由于宽度变小，迎水壁面压力突变，压力要大于附近；而下游处收缩断面由于宽度变大，出现了压降，压力要小于附近。在闸孔至下游0.6m区域内，受水流冲击，此处的压力分布也显示出不稳定性。