弧形闸门开度计算

代 威

（1太原理工大学 山西太原030024；2山西省水利水电勘测设计研究院 山西太原030024）

1 问题的引出

弧形闸门是一种应用十分广泛的闸门类型，具有结构简单、启门力小、水流条件好等优点，常被用于泄水建筑物上作为工作闸门使用。然而也正是因为闸门启闭时门叶绕固定水平铰轴转动，致使弧形闸门开度的计算并不像平面闸门的那样简单。

作为设计人员，经常会需要知道几个数据：1）当闸门提起一定高度时，启闭机此时将滑轮组提升了多高。2）当闸门完全提出孔口进入检修工位时，此时滑轮组提升了多少，即启闭机所需的最小行程是多少。3）当闸门提起一定高度时，闸门顶部提升了多少，当闸门提升多高时，闸门顶部就脱离了门槽限位。4）当闸门完全提出孔口进入检修工位时，此时门顶的相对高度是多高，会不会与启闭机下部混凝土大梁发生干涉。5）当一个拦河闸全部提出孔口泄流时，此时闸门顶部与启闭机房的相对位置关系又是怎样的。

几年前，笔者也曾面对过这些问题，当时作为“设计”，完全可以通过精确制图来回答这些问题。但是如果设计人员通过制图法得出了上述问题的结论，那么校核人员仍然用制图法校核，审查人员还是用制图法审查，那么恐怕有些不妥。其实通过几何推导，一样可以解决这些问题，而且通过计算机简单的编程，其效率远高于用精确制图法。

由于弧形闸门的特殊性，闸门面板曲率半径一般不等于吊耳曲率半径，故笔者上述的5个问题中，分两类:一类是启闭机行程与闸门开度的关系，即问题1与2；另一类是闸门门顶运行高度与闸门开度的关系，即问题3～5。下面将分别推导总结，推导中用到的数据全部为闸门总图、闸门及启闭机联系图内可方便读出的，且为必须标注的关键尺寸。

2 公式的推导

2.1 启闭机行程与闸门开度的关系

已知：

R—弧形闸门面板外缘曲率半径，mm；

R’—弧形闸门吊点所在位置曲率半径，mm；

A—弧形闸门支铰高度，mm；

H0—弧形闸门吊耳初始高度，mm；

X—起吊中心线距支铰中心水平距，mm；

Y—启闭机距支铰相对安装高度，mm；

h—闸门开度，mm。

另，O0为闸门关闭时，吊耳所在位置；

O1为闸门开度为h时，吊耳所在位置；

Q点为启闭机吊点所在位置。

求：

L—启闭机行程，mm；

具体内容见图1。

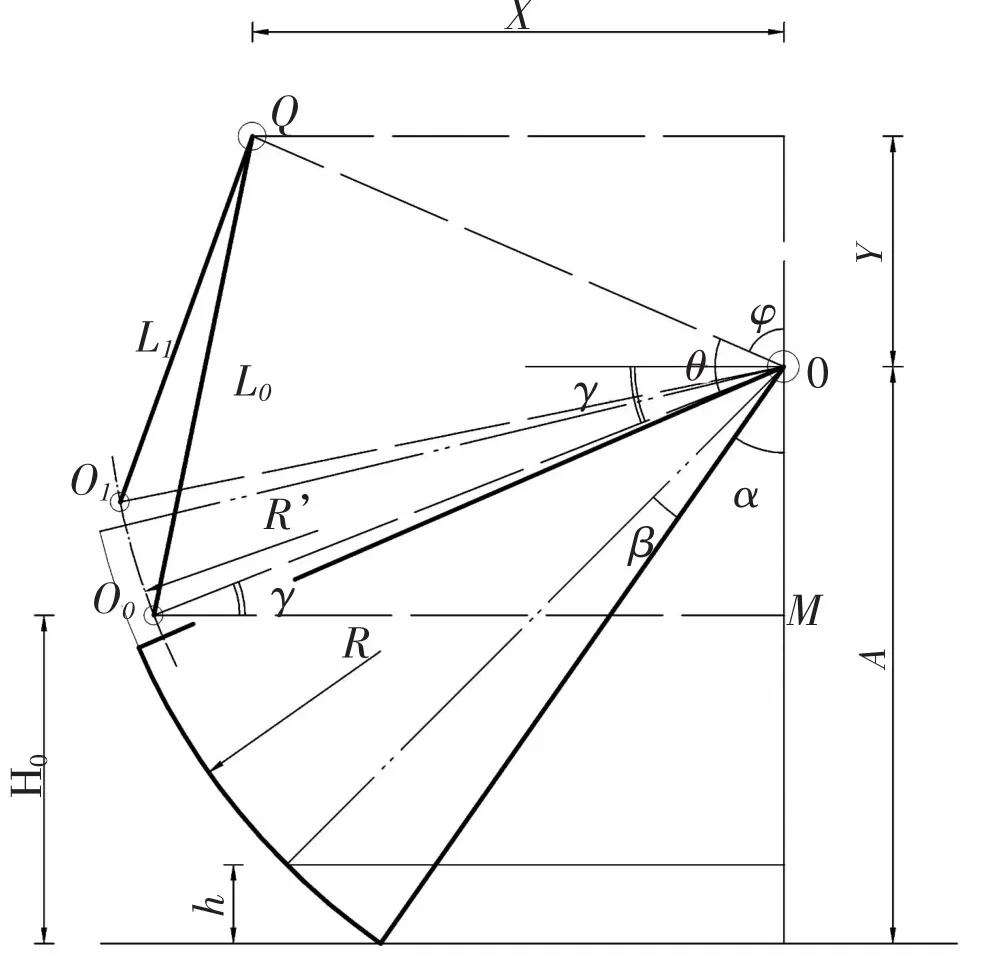
图1 启闭机行程计算图

推导公式过程如下：

由图1可知：

此时L0即为闸门关闭状态下钢丝绳组的初始伸长；

当闸门开启h高度时，门体转过的角度即为β角，故有：

此时L1即为闸门开度为h状态下钢丝绳组的伸长；

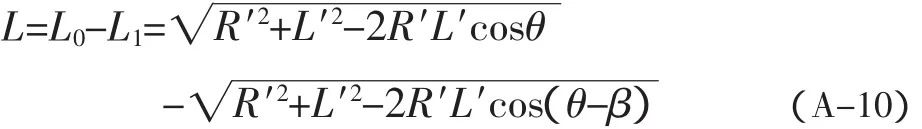
将（A-3）、（A-6）、（A-7）带入（A-10）可得 L 的最终计算结果。

L值即为在h开度下，启闭机的实际行程，当h取极大值时，所对应的L值即为启闭机的最小行程。

注：（A-4）式中，当吊耳高度高于支铰高度时，所有公式均不改变，此时仅仅为负数而已。

2.2 闸门门顶运行高度与闸门开度的关系

已知：

H—弧形闸门面板高度，mm；

LC—弧形闸门面板总弧长，mm；

h—闸门开度，mm；

其余同上。

求：

g—门顶启升高度，mm。

具体内容见图2。

图2 门顶启升高度计算图

推导公式过程如下：

由图2可知：g+H=H′+h

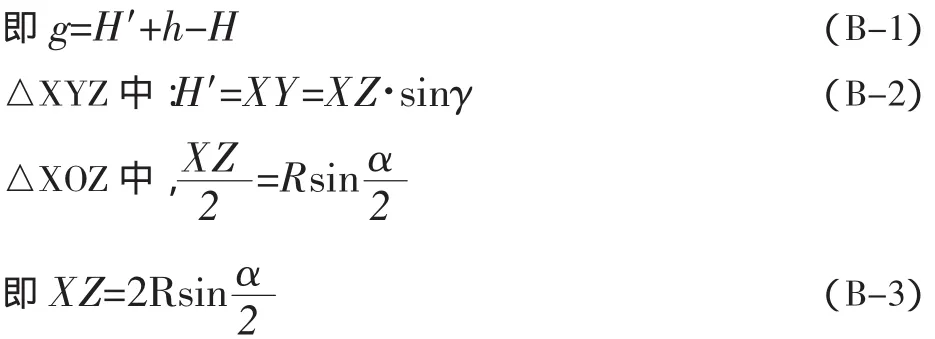
将（B-3）带入（B-2）中，可得：

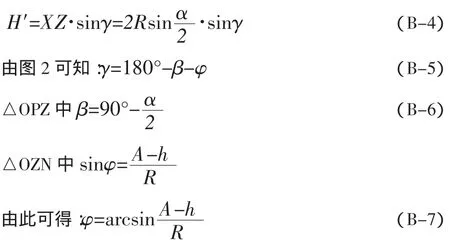
将（B-6）、（B-7）带入（B-5）中，可得：

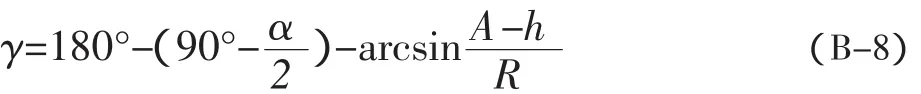
将（B-8）带入（B-4），可得：

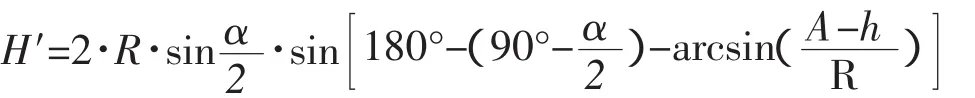
化简得：

将（B-9）带入（B-1），可得：

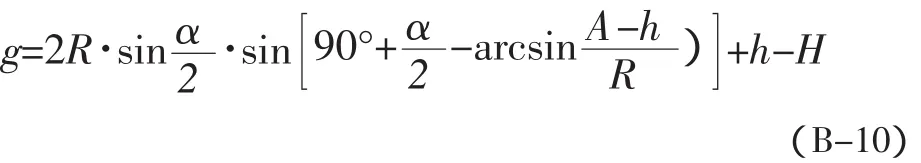
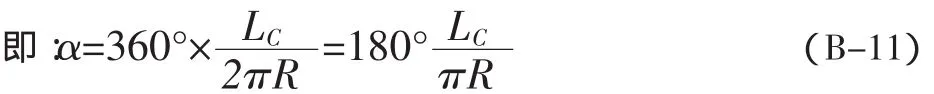
将（B-11）带入（B-10），可得：

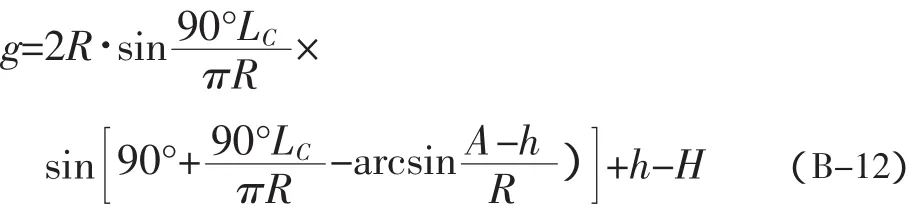
g值即为在h开度下，闸门门顶的启升高度。

3 应用举例

不论是（A-10）还是（B-12）看似公式有些繁琐，但是在计算机高度发达的今天，通过简单地Excel表格，使用一个仅需2×12的表格，将已知数据输入，立刻就能得到想要的数据。现以山西省晋中地区某水库底孔弧形工作闸门为例做以简单说明。

已知数据：R=9000 mm，H=5230 mm，A=6000 mm，LC=5797mm，H0=5500 mm,R’=8376mm,X=7477mm,Y=9323mm。将闸门提至极限位置即检修工位时，h=5800 mm。此时将数据带入（A-11）、（B-12）公式可得：L=5582mm，g=6094mm。考虑到余量，闸门实际选用启闭机行程5900 mm，启闭机平台净空高度6623mm。

本文中L及g的应用非常广泛，上例中仅计算了闸门极限位置是对应的关系。在实际应用中，通过计算机可以很容易地制作一张附表，附在“闸门与启闭机联系图”上，有了这样的表格，弧形闸门的开度就可以方便的控制，不但使得工程验收时对闸门开度控制有据可循，也便于运营管理部门平时对闸门运行时的开度进行较好的控制。