加载位置对道砟静态压碎形式的影响研究

张振超，赵春发，张 徐

(西南交通大学牵引动力国家重点实验室，四川成都 610031)

散体道床是铁路有砟轨道重要组成部分，它由满足一定粒径级配和强度要求的碎石道砟堆集而成，在轨道结构中起到分散轮轨集中荷载的作用。近年来，我国铁路高速化、重载化发展迅猛，在高密度、大轴重列车荷载作用下，道床承受的振动与冲击作用加剧，导致道砟破碎、粉化以及道床沉降、脏污、板结等病害问题更加突出，需要开展道砟力学行为及其磨损、破碎等机理研究，为高速及重载散体道床结构设计与维护提供指导。

国内外采用道砟箱或小尺寸道床结构开展了大量的室内试验及数值模拟分析，但由于道砟几何形态的随机性和物理力学性能的离散性，大多数研究集中在道床宏观力学行为与性能方面，对道砟破碎、磨损及粉化等现象研究不多［1-2］。Lim 等［3］对6类道砟进行单轴压碎试验，采用Weibull概率统计得到不同尺寸等级道砟颗粒的特征强度;苏勇［4］对一定粒径范围的石灰岩道砟进行单轴压碎试验，得到道砟颗粒强度与其尺寸的关系;Lobo-Guerrero等［5］对循环荷载作用下的道床特性进行模拟分析，比较了道砟可破碎和不可破碎两种情况下的道床沉降特性;Hossain等［6］建立几种简单颗粒的二维离散元模型，分析了道砟破碎对永久变形的影响;Lackenby等［7］通过室内三轴试验分析了围压对道砟破碎及变形的影响;Lu等［8］建立道砟动三轴试验数值模型，在考虑道砟破碎和表面磨损的情况下分析了不同围压对道砟集料变形的影响。井国庆等［9］采用简单颗粒组合模拟道砟，研究了不同黏结强度下道砟破碎对沉降的影响。这些研究有利于认清道砟力学性能与状态变化对道床结构性能的影响，但没有关注道砟破碎力学行为本身及其影响因素。

本文采用颗粒流分析软件PFC2D，建立单颗粒道砟的离散元模型，通过模拟不同位置加载情况下道砟的静态压碎行为，分析了外部接触与受力状态变化对道砟压碎过程及其破碎形式的影响。

1 道砟单轴压碎的离散元模型

1.1 道砟外形模拟与填充

碎石道床由形状不规则、带有棱角的道砟颗粒组成，颗粒形态对道砟之间接触及受力状态有重要影响，因此，道砟力学行为数值模拟应尽量考虑其真实几何外形。本文采用数码相机对道砟试验样本进行拍照(图1)，然后对获得的图像进行二值化处理［10］，在此基础上使用颗粒流分析软件PFC2D，建立道砟二维离散元模型，如图2所示。

图1 道砟样本

图2 道砟离散元模型

模型中采用了六边形密排圆盘单元填充道砟样本的二值化图像，显然，圆盘半径越小，道砟颗粒外形的模拟精度越高，但这会降低模型计算效率，两者权衡后选取圆盘单元半径为1 mm。

1.2 本构关系及参数选取

道砟材料的本构关系是通过定义单元间接触、滑动和黏结模型来实现的，正常条件下道砟颗粒之间并没有黏结，因此，颗粒间只需定义接触与滑动模型，但道砟内部单元之间仍需要定义黏结模型。本文采用线性接触模型，其刚度由接触杨氏模量确定;滑动模型依据莫尔—库伦强度理论建立，通过定义两接触体之间摩擦系数确定;单元间黏结模型采用了只能传递力的接触黏结模型［11］。

根据花岗岩道砟材质的物理力学性能，选取其接触杨氏模量为65 GPa，抗拉强度20 MPa，切向强度20 MPa，计算得到道砟离散元模型参数，见表1。

表1 道砟离散元模型参数

1.3 加载方式与加载位置

在道砟离散元模型上、下方分别生成墙体，模拟道砟单轴加载试验，墙体的法向和切向刚度均取5×1010N/m，表面摩擦系数取0.5。试验过程中底面墙体固定不动，起支承作用，上方墙体(加载板)以恒定速度向下移动，加载速率为1 mm/s。

同一颗道砟在道床中所处姿态不一样，其接触与受力状态不同，这会导致道砟破碎、磨损等力学行为也不一样，并影响到道床宏观力学性能与状态的变化。本文建立了5种位置加载时道砟单轴压碎试验数值模型，见图3。其中，在位置1加载时，道砟顶部和底部均为平面接触，上下受力面大小相近;位置2与位置1情况相似，但上受力面较小，相当于上棱角、下平面受力;在位置3和位置4加载时，道砟上下接触处均为棱角，但位置3时上、下接触处棱角更为突出;在位置5加载时，上下接触中心连线与竖向加载方向有明显夹角，且底部接触面存在一定的表面纹理。上述5种位置可以归分3类:位置1和位置2为第1类，位置3和位置4为第2类，位置5为第3类。

图3 5种位置加载时道砟单轴压碎试验的离散元模型

2 道砟单轴压碎过程分析

花岗岩试样单轴压缩至破坏的过程可分为5个阶段:微裂纹压密阶段、弹性变形阶段、裂纹初始阶段、裂纹稳定扩展及裂纹不稳定发展阶段。本文道砟离散元模型没有考虑初始缺陷，模拟结果将不能反映微裂纹压密阶段。

以在位置1加载时道砟压碎行为为例，分析道砟颗粒压碎过程。图4和5给出了道砟压碎过程不同阶段的力链分布图和黏结断裂分布图。图4中ε表示轴向应变，F表示荷载，线条粗细表征力的大小;图5中N表示黏结断裂数。图4显示，在道砟静态压缩初期，道砟处于弹性变形阶段，荷载力和单元间接触力随轴向应变增加而增大，力链分布均匀，上下接触表面的应力集中现象较明显。当轴向应变达到0.08%之后，道砟内部形成断裂面，载荷力随轴向应变增加而快速减小，道砟发生破碎后力链逐渐恢复到自然状态。图5清晰反映了道砟内部裂纹发生、稳定发展到贯穿整个道砟的过程。当道砟轴向应变为0.05%时内部黏结断裂数仅为12个;轴向应变增加到0.07%和0.08%时，黏结断裂数分别达到96个和181个，内部裂纹从上、下接触处向内部稳定扩展的趋势非常明显;当轴向应变为0.15%时，黏结断裂数为409个，此时裂纹已贯穿整个道砟。

图4 位置1加载时力链分布及其发展

图4和图5显示，道砟压碎过程中内部裂纹萌生与发展是一个逐步积累的过程，断裂面由上下接触处微裂纹扩展而成，断裂面扩展方向和速率与内部力链分布、黏结断裂增长速度有关。

图5 位置1加载时黏结断裂分布及其发展

3 加载位置对道砟压碎行为的影响

3.1 对道砟抗压强度的影响

采用McDowell等提出的最大诱导应力来表示道砟单轴抗压强度［12］，此概念来源于Jaeger提出的颗粒诱导应力［13］。其值为加载板上作用力与加载板和底座之间距离平方的比值。诱导应力主要反映荷载力大小，并不是道砟内部真实应力。

图6是在位置1～5加载时道砟诱导应力与轴向应变的关系曲线。可以看出，尽管加载位置不同，但所有曲线的波形基本相似，但不同加载位置得到的道砟最大诱导应力(抗压强度)差别较大。以诱导应力达到最大时作为分界点(称之为破碎临界点)，在临界点之前，道砟诱导应力均随轴向应变呈线性增长，表明道砟处于弹性变形阶段;在临界点之后诱导应力随轴向应变急剧减小，此时道砟破碎，随后诱导应力缓慢趋近于0。需要指出的是，在位置2加载时道砟压碎过程中出现了二次应力峰值，这是因为道砟先后出现了两个破裂面，但第一次破碎之前和第二次破碎之后的诱导应力与轴向应变关系曲线的走势不变。

表2给出了在不同位置加载时道砟压碎过程中的应力应变与黏结断裂数。5种加载位置时道砟单轴抗压强度分别为 21.56，27.91，7.10，8.86 和 4.78 MPa，说明在第1类位置加载得到的抗压强度明显大于其它2类位置，第3类位置最小;在位置2加载时的道砟抗压强度是位置5的5.8倍，可见道砟单轴抗压能力受加载位置的影响显著。这是因为不同加载位置时道砟接触与受力状态差异显著，并影响到道砟内部力链的分布，导致道砟破碎形式与方式不一样。例如，当加载位置为棱角时(位置3和4)，道砟表面接触面很小，力链路径窄，局部应力集中现象明显，道砟容易发生破碎;当道砟上、下加载位置连线有明显倾斜时(位置5)，道砟实际上受到了较强的剪切作用，此时道砟更容易破碎，单轴抗压强度也最小。

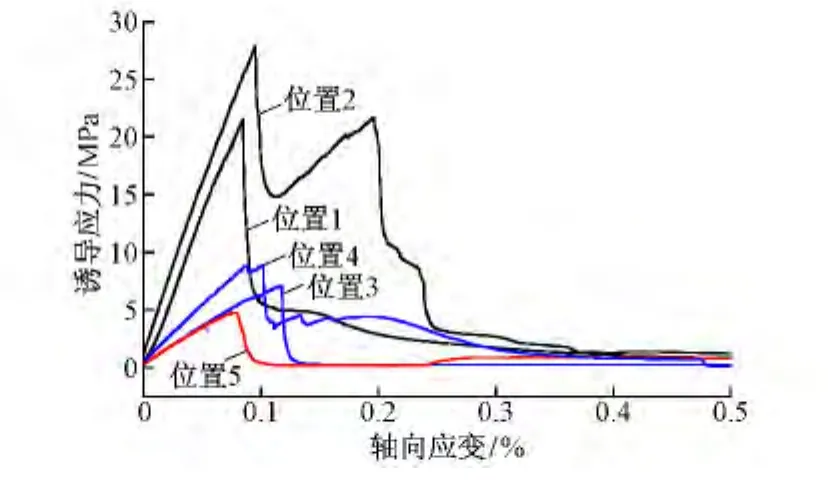
图6 道砟诱导应力与轴向应变关系

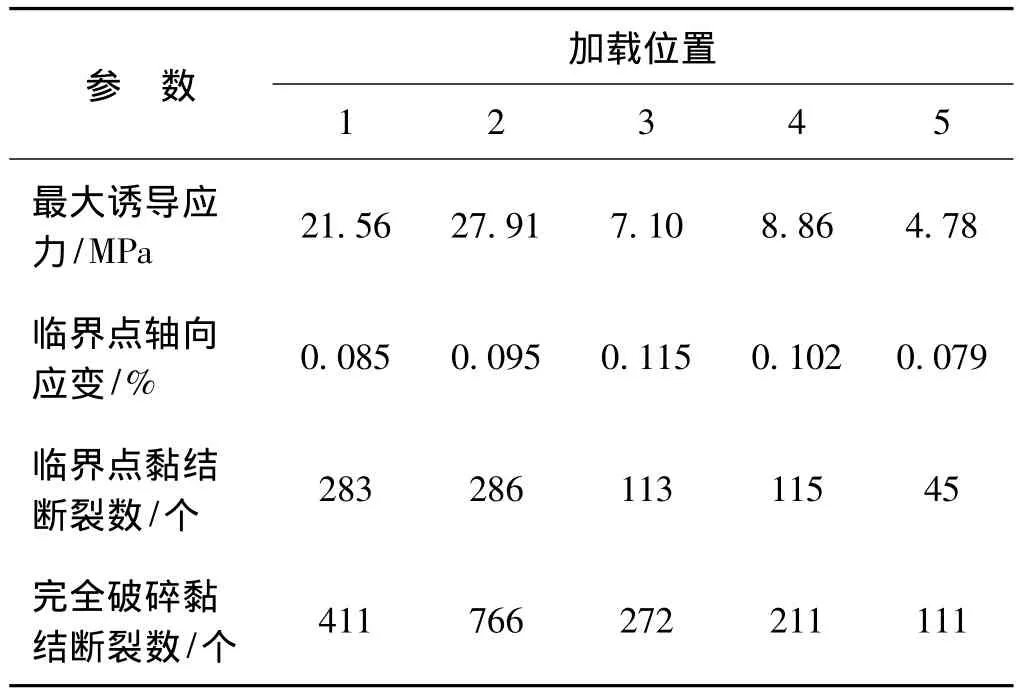
表2 道砟压碎过程中应力应变与黏结断裂数统计

由表2还可知，在5种加载位置时破碎临界点处道砟黏结断裂数分别为283，286，113，115 和45，说明道砟抗压强度越大，破碎临界点处对应的黏结断裂数越大。但是，破碎临界点处道砟轴向应变值并没有随抗压强度发生规律性变化。

3.2 对道砟压碎过程的影响

图7和图8分别为道砟压碎过程中黏结断裂数与轴向应变和诱导应力的关系曲线。图7表明，5种加载情况下道砟黏结断裂数与轴向应变曲线的变化趋势一致;但是，加载位置的类别不同，黏结断裂数初期增速不同，第1类位置时黏结断裂数初期增速大于其它2类位置，说明道砟抗压强度越大，黏结断裂数初期增速越大。此外，不同位置加载时道砟破碎后的黏结断裂数差别较大，表明道砟破碎时裂纹扩展规模或断裂面大小有明显差异;同样，如果该位置类别对应的抗压强度越大，破碎时黏结断裂数越多。

图7 压碎过程中黏结断裂数与轴向应变关系

图8 压碎过程中黏结断裂数与诱导应力关系

由图7还可见，对所有加载位置而言，道砟压缩到破碎临界点之前，黏结断裂数随轴向应变稳定增长，反映了内部裂纹的稳定生长;在道砟破碎过程中，黏结断裂数随轴向应变增加而增长的速度没有规律，说明内部裂纹扩展是不稳定的。

图8显示道砟内部黏结断裂数与诱导应力关系曲线变化趋势相似(位置2除外)。在不同位置加载时，关系曲线的幅值主要由最大诱导应力来决定，即道砟抗压强度越大，破碎临界点的黏结断裂数也越大。由图8还可见，道砟静态受压初期，黏结断裂数随诱导应力的增加缓慢增长，此阶段包含了内部裂纹的萌生及其初期缓慢生长;当诱导应力达到抗压强度的70%左右时，黏结断裂数增速明显加快，裂纹快速稳定扩展;当诱导应力达到最大以后，黏结断裂数仍在增长，但诱导应力却迅速减小，表明内部断裂面已形成并快速贯穿道砟。

3.3 对道砟破碎形式的影响

岩石试样的压碎破坏形式主要有4类:X状共轭斜面剪切破坏、单斜面剪切破坏、延性破坏和拉伸破坏。道砟破碎形式也应与其类似，而加载位置的改变有可能导致道砟破坏形式的改变。

图9是道砟压碎后的黏结断裂分布图。可以发现，加载位置对道砟黏结断裂的分布及其数量均有显著影响。在位置1加载时，道砟内部黏结断裂主要是拉伸失效，破碎时生成贯穿的剪切失效面，道砟破坏形式属于拉伸破坏。在位置2加载时，道砟压碎后其内部出现2个贯穿的断裂面，黏结断裂仍以拉伸失效为主，且黏结断裂数量是所有加载位置中最多的，道砟破碎形式仍属于拉伸破坏。在位置3和位置4加载时，上下棱角处因为应力集中出现了一定数量的拉伸失效，但断裂面中部是较为单纯的剪切失效，其破碎形式属于单斜面剪切破坏。在位置5加载时，道砟内部出现了很少的拉伸失效，仅在上下加载位置连线上生成剪切失效面，该剪切面与加载方向(竖向)夹角较大，道砟破碎属于单斜面剪切破坏。

图9 道砟压碎后的黏结断裂分布

以上分析表明，因为几何形状不规则，道砟以不同姿态静态受压时，上下表面接触状态及其接触面相对位置影响了道砟内部力链的分布。尽管这对道砟静态压碎过程影响不明显，但可能导致道砟破碎形式完全不一样，使得单颗道砟的抗压强度差别很大。

4 结论

通过模拟不同位置加载时道砟的静态压碎行为，比较分析了加载位置对道砟抗压强度、压碎过程以及破碎形式的影响，得出如下结论:

1)离散元模型能较好模拟道砟压碎过程中的弹性变形、裂纹萌生、裂纹稳定发展和不稳定扩展。不同位置加载时，贯穿道砟的断裂面均由上下接触处微裂纹扩展而成，断裂面扩展方向和速率与道砟内部力链分布、黏结断裂增长速度有关。

2)加载位置对道砟单轴抗压强度影响显著。上下加载位置为平面时，内部受力较均匀，道砟压碎需要的荷载较大，其单轴抗压强度要明显大于加载位置为棱角时;当加载位置中心连线与加载方向有较大夹角时，道砟容易发生剪切破坏，其单轴抗压强度最小。

3)道砟在不同位置加载时，其内部力链分布发生变化，导致道砟破坏形式有可能发生改变。当道砟有较稳定的加载平面时，内部黏结断裂以拉伸失效为主，道砟易发生拉伸破坏;当受力位置为棱角或上下加载位置中心连线与加载方向夹角较大时，道砟很容易发生单斜面剪切破坏。

［1］INDRARATNA B，SALIM W．Mechanics of Ballasted Rail Tracks:A Geotechnical Perspective［M］．London:Taylor＆Francis Group，2005．

［2］曾树谷．铁路散粒体道床［M］．北京:中国铁道出版社，1997．

［3］LIM W L，MCDOWELL G R，COLLOP A C．The application of Weibull statistics to the strength of railway ballast［J］．Granular Matter，2004，6(4):229-237．

［4］苏勇．含沙铁路道碴力学行为研究［D］．大连:大连理工大学，2011．

［5］LOBO-GUERRERO S，VALLEJO L E．Discrete element method analysis of railtrack ballast degradation during cyclic loading［J］．Granular Matter，2006，8(3-4):195-204．

［6］HOSSAIN Z，INDRARATNA B，DARVE F，et al．DEM analysis of angular ballast breakage under cyclic loading［J］．Geomechanics and Geoengineering:An International Journal，2007，2(3):175-181．

［7］LACKENBY J，INDRARATNA B，MCDOWELL G，et al．Effect ofconfiningpressureon ballastdegradation and deformation under cyclic triaxial loading［J］．Géotechnique，2007，57(6):527-536．

［8］LU M，MCDOWELL G R．Discrete element modelling of railway ballast under monotonic and cyclic triaxial loading［J］．Géotechnique，2010，60(6):459-467．

［9］井国庆，封坤，高亮，等．循环荷载作用下道砟破碎老化的离散元仿真［J］．西南交通大学学报，2012，47(2):187-191．

［10］付招兴．高速铁路道砟形态特征量化方法及其应用研究［D］．成都:西南交通大学，2013．

［11］Itasca Consulting Group，Inc．PFC3DVersion 4.0 Theory and Background［Z］．Minneapolis:Itasca Consulting Group，Inc．，2008．

［12］MCDOWELL G R．LIM W L，COLLOP A C．Measuring the strength of railway ballast［J］．Ground Engineering，2003，36(1):25-28．

［13］JAEGER J C．Failure of rocks under tensile conditions［J］．International Journal of Rock Mechanics and Mining Sciences＆ Geomechanics Abstracts，1967，4(2):219-227．