钢轨在轮轨力作用下的垂向应力响应特性

2014-12-25焦振华戴恒震周文静

铁道建筑 2014年11期

焦振华，戴恒震，刘冲，周文静

(大连理工大学，辽宁大连 116024)

无缝线路轨道因消除了大量的钢轨接头，具有列车行驶平稳性好、线路养护维修费用低和使用寿命长等优点，因而广泛地应用于高速铁路轨道结构中，这也是目前我国高速铁路轨道结构发展的重点。无缝线路钢轨因扣件和道床的约束，轴向不能自由伸缩，当钢轨温度升高或降低时，钢轨内部产生轴向压力或拉力，在车轮荷载作用下，可能导致钢轨胀曲或断轨，严重影响行车安全［1-2］。卢耀荣［3］在环形试验基地进行温度力和列车动载共同作用下动态稳定性试验，试验中发现无缝线路动态失稳有别于静态失稳的特征。钢轨的垂向应力间接反映了动态荷载，采集分析钢轨的动态响应，对无缝线路失稳的研究有指导意义。国内外关于钢轨动态的研究大多集中在车辆超偏载［4］和钢轨的固有频率与温度力［5］的关系。目前，还没有针对性地研究钢轨的垂向应力响应与列车车轮荷载之间的关系。

本文采用Abaqus有限元软件［6-7］建立无砟轨道的三维有限元模型，仿真分析了不同荷载作用下的钢轨轨腰处的垂向应力响应，并通过轮轨力加载试验台进行试验验证，得到了钢轨在不同荷载作用下，轨腰处的垂向应力响应的分布规律。

1 轮轨力加载试验台及有限元模型

1.1 轮轨力加载试验台

图1 轮轨力加载试验台及控制器

轮轨力加载试验台如图1所示。试验台主要由高速铁路轨道、轮轨力加载装置、控制器等组成。其中高速铁路轨道是严格按照哈大线的施工标准铺设而成的一段长20 m无砟轨道［8］。该无砟轨道由地基、CA砂浆、CRTSⅠ型轨道板、铁垫板、橡胶垫、扣件、钢轨等组成;轮轨力加载装置主要包括电液伺服作动器、控制器、压力反馈传感器和轮轨力加载头等组成。电液伺服作动器(型号:WSNF3A050T，主要性能指标:最大静态试验力为80 kN，频率范围为0.1～30.0 HZ)用于模拟列车车轮对钢轨的荷载。电液伺服作动器可通过控制器进行程式控制，模拟列车车轮对钢轨的静态或动态荷载。与钢轨接触的轮轨力加载头底面形状与列车车轮的踏面类似，以模拟列车车轮与钢轨的相互作用关系。

1.2 轨道试验台有限元模型

本文按照 CRTSⅠ型板式无砟轨道结构，在Abaqus有限元仿真软件中，建立了一段长度为5 130 mm的无缝线路仿真模型。有限元模型如图2所示。有限元模型车轮定义为分析刚体，其它各部件采用一阶六面体减缩积分单元C3D8R进行有限元划分，全局种子布置为30 mm，在钢轨的横截面及存在接触部位采用局部网格进行细化。各部件的材料属性如表 1 所示［9-10］。

图2 三维轮轨接触有限元模型

表1 无砟轨道模型各部分材料性质

分析过程中，选用静态通用分析步［11］。首先，在初始分析步定义好各部件之间接触关系及边界条件;其次，在第一分析步中定义重力场并在扣件上施加9 kN［12］的等效扣压力。从第二分析步开始，依次给车轮轴的中心参考点位置施加 60，80，100，120，140 和160 kN的车轮载荷，并分析钢轨在不同荷载作用下轨腰处的垂向应力响应。

2 有限元结果及其分析

本文主要研究无砟轨道钢轨在不同荷载作用下的垂向应力分布。选用如图2所示的坐标系，X为横向、Y为垂向、Z为轴向。根据坐标轴的定义，则S22表示钢轨的垂向正应力。图3至图6分别为钢轨的Mises综合应力和S22方向的正应力云图，车轮载荷为120 kN。从图3和图4中可以看出由于钢轨的工字型的特殊结构，在车轮载荷作用下，钢轨的垂向应力响应规律与采用矩形梁单元模拟分析得到的结果［4］存在差异。相比于矩形梁单元模型的分析结果，钢轨在不同荷载作用下，轨头与车轮接触区域的应力比较集中，除轨头与车轮接触区域外，垂向应力响应的最大区域分布在钢轨的跨中，轨腰内侧最上方。

图3 车轮荷载作用下轨腰外侧Mises应力分布

图4 车轮荷载作用下轨腰内侧Mises应力分布

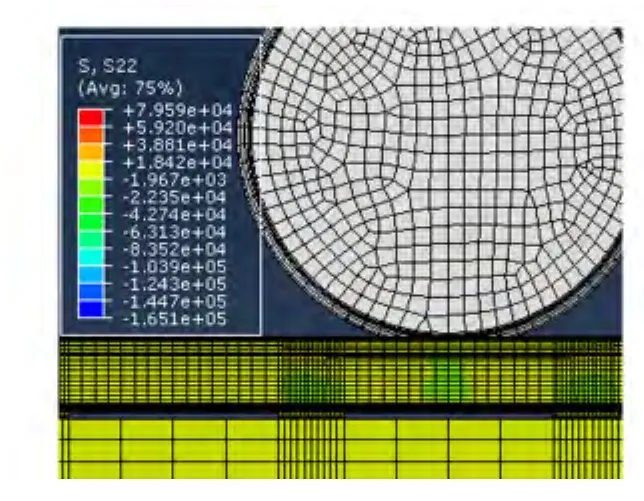
图5 车轮荷载作用下轨腰外侧S22应力分布

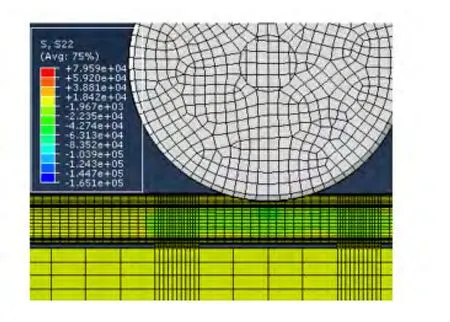
图6 车轮荷载作用下轨腰内侧S22应力分布

由于钢轨的轨头及轨底刚度较大，在车轮荷载作用下，轨腰处腹板区域的Mises主应力大约成45°分布在车轮荷载位置正下方的两侧。钢轨轨腰处的垂向应力最大区域分布在车轮荷载处轨腰最上方，如图5和图6所示。

选择车轮荷载当前作用跨，对一跨钢轨轨腰内侧上、中、下和轨腰外侧上、中、下的垂向应力进行分析，如图7所示。从图中可以看出，在轨底以上部分，轨腰内侧的垂向应力明显大于轨腰外侧;在钢轨的同一侧，轨腰上方的垂向应力响应大于轨腰下方。

图7 轨腰内侧和轨腰外侧S22正应力分布

根据图7中的分析结果，分别从模型中选取车轮荷载作用跨的跨中，轨腰内侧距离轨底平面高度分别为60，82，100，120 mm 处的4个位置点，分析钢轨的垂向应力与轮轨力之间的关系。如图8所示，图中4条曲线分别表示以上选取的4个位置处的垂向应力与车轮荷载大小之间的关系。从图8可以看出，在不同荷载作用下，钢轨的垂向应力响应与荷载大小基本成线性关系;在同一荷载作用下，钢轨垂直方向的同一横截面内，从钢轨的轨腰上侧至下侧，垂向应力响应变小。

图8 不同荷载作用下轨腰内侧垂向应力

3 试验验证及分析

为进一步验证以上有限元模型的分析结果，本文利用轮轨力加载试验台对钢轨进行加载试验，模拟列车车轮对钢轨的荷载作用。试验前，在轮轨力加载头的下方，轨腰内侧粘贴“共和”应变片，应变片的安装位置选择在钢轨的跨中，距离钢轨底部平面的高度分别为120，100，82和60 mm的位置。应变片安装完成后，利用无线传感网动态应变采集节点进行数据采集，应变片按照惠斯通半桥接法，采集频率为500 Hz，采集方式设置为实时采集。

试验前将荷载大小设置为0，对动态应变采集节点也清零后，分别按照 30，40，50，60，70，80 kN 的顺序依次给钢轨施加车轮荷载，记录钢轨轨腰内侧4个位置处应变片采集到的应变值大小。利用应变与应力和弹性模量之间的关系，将以上试验采集到的4个位置点的垂向应变转换成应力，与仿真计算结果进行对比，如图9所示。图中实线为试验结果，虚线为仿真计算结果。从图9可知，仿真计算结果与试验得到的结果吻合较好，误差在5%以内，垂向应力大小与钢轨所受车轮荷载基本成线性关系。