一种新的手写汉字生成方法
2014-12-25吕振伟
吕振伟
(太原学院 基础部,山西 太原030032)
0 引言
手写汉字的研究一直是模式识别领域的一个热点问题,已经有大量关于手写汉字识别的研究工作,但是手写汉字生成的研究并不多。同时,手写汉字生成的研究有其一定的意义,例如可以用来构建汉字数据库等等,因此本文将研究如何生成具有一定风格的汉字的问题。
手写汉字生成的比较早的工作来自于文献[1],其中把汉字分为了五层,分别为结构椭圆、简单笔划、复合笔划、偏旁部首和单字,在对训练样本的几个离散风格进行学习建立风格的模型以后,新的风格由训练样本风格的线性插值来表示,给定不同的参数就可以生成不同的风格。文献[2]把汉字分为两层,即笔划和单字,然后分别建立笔划和单字的统计模型。每一个笔划由表示笔划的特征点的概率密度函数来表示,而每一个单字由组成单字的笔划的联合概率密度函数来表示,但该模型太复杂,不易试验和操作。
本文也运用汉字的统计结构模型,把汉字分为三层:笔划、部首和单字,然后分别建立三个层次的统计模型,最后基于HCL2000汉字数据库来验证模型的有效性。
1 手写汉字生成的研究
因为手写汉字存在大小和倾斜等问题,所以需要对汉字进行匹配预处理以后才可以进行汉字的生成研究,对手写汉字进行预处理,其中包括汉字特征点的提取和汉字的匹配。由汉字结构可知,汉字由部首或笔划表示,部首由组成它的笔划表示,而笔划由组成它的特征点表示,特征点的提取由手工来完成。我们首先是建立汉字的统计模型,这主要运用主成份分析[3](PCA)和核主成份分析[4](KPCA)的方法,然后从统计模型中生成汉字,见图1汉字生成的系统结构图。
1.1 笔划的统计和生成
设某一笔划的样本为x1,…,xl,其中xi由M 个点组成,记 xi=(xi1,yi1,xi2,yi2,…,xiM,yiM),设 x1,…,xl为已匹配的笔划样本,运用KPCA对笔划的形状进行统计,可得笔划的模型:Vkφ(x)=Vkγ + ¯φ,其中γ为K维参数向量,它服从K维独立正态分布,即γ~N(0,Λ)。Vk是由V中前k个最大特征值对应的特征向量组成的矩阵,V是中心化核矩阵~K的特征向量矩阵,¯φ 是样本均值[6]。
有了笔划之后,我们接着讨论用笔划生成部首。设每一个笔划都用它的外部轮廓来表示,即用包括该笔划的矩形来表示.设矩形对角顶点的坐标表示为(x1,y1,x2,y2)。首先,对某一部首的样本进行匹配,然后应用新模型研究组成部首的各个笔划之间的相对大小和位置,设部首由m个笔划组成,每个笔划的矩形轮廓用(xi1,yi1,xi2,yi2),i=1,…,m 来表示,每个笔划包含的相对大小和位置关系xi用它的矩形轮廓和起点和终点来表示,设起点为(xis,yis),终点为(xie,yie),则 xi=(xi1,yi1,xi2,yi2,xie,yie,xis,yis),用X表示部首的各个笔划之间的相对大小和 位置关系,设部首有l个样本,我们建立新模型:

图1 汉字生成系统结构图

其中η为参数向量,它服从正态分布,即η~N(0,Λ),其中Λ是对角线为特征值的对角矩阵;ε=(ε1,…,εl)是误差变量,也可以把它看作噪声变量,它服从多维独立分布,且若ηi>0,则εi~N(0,σ2),其中,若 ηi=0,则 εi=0,1 ≤ i≤l,且η和ε独立,V是由特征向量组成的矩阵,这里假设它的列向量按特征值由大到小的顺序排列,Vk是由V的前k个最大特征值对应的特征向量组成的矩阵。给定某一参数η,可以用最小二乘法,求使得下式最小的。
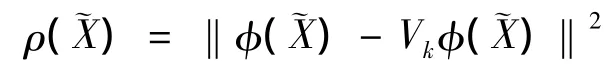
可以得到对应的部首中各个笔划之间的相对大小和位置关系。
1.2 部首的统计
部首的统计模型由两部分组成,第一部分是由在训练样本集上得到的部首的形状统计模型,它在所有部首样本上进行统计,而不是在各个风格子集上进行统计,因此得到的模型是对部首形状的整体统计,表示部首的一般形状,第二部分要用到测试样本集中的信息,此部分建立在各个风格子集上,它研究同一部首在不同汉字中的关系,本文假设这个关系与风格无关,所以我们只建立第二部分的模型,我们运用PCA来研究这个问题。
假设要研究的部首为r,要研究的汉字为w1和w2,则要研究的关系是给定w1的部首r之后,求出w2的部首r.设训练样本集上的风格为S1,…,Sm,即训练样本集共有m个风格.设某一风格S的样本子集中 w1,w2的样本数分别为 k1,k2,其中 S表示 S1,…,Sm中的任一风格,r是由特征点表示的n维向量,汉字w1中的笔划r记为r1,w2中的笔划r记为r2,要研究r1和r2的关系,首先建立样本对(r1,r2),显然共有k1×k2个这样的样本对,然后对部首r的各个笔划和部首中笔划的相对大小和位置关系进行匹配,这通过仿射变换来完成。设Δr=r2-r1,则风格S共有k1×k2个样本Δr,其中Δr包括两部分,一部分式r对应笔划的差另一部分式部首中笔划的相对大小和位置关系的差。
对样本集Δr进行PCA可得模型:Δr=μ+Ukb+ε,其中b是参数向量,它服从正态分布,即b~N(0,Λ),其中Λ是对角线为特征值的对角矩阵;ε是误差变量,也可以把它看作噪声变量,它也服从正态分布,即 ε ~ N(0,σ2I),其中,且 b和ε独立。
设在风格Si下模型为,假设研究的关系和风格独立,则Δr的统计模型如下:g(Δr)= ∫f(Δr|S)f(S)dS,这里假设各个风格的先验概率相等,因为共有m个风格,所以设每个风格的概率为,则g(Δr)可近似表示为:

由此我们得到了统计模型g(Δr)。假设在训练样本集上得到的部首的整体形状的模型为h(r),此处得到的部首模型仍然是由部首中的笔划和笔划之间的相对位置的大小模型组成,而KPCA和新模型不易求出在原样本空间对应的形状的显示表达式,所以不能通过公式f(r)=λg(Δr)+(1-λ)h(r)来直接求出部首的统计模型,为此我们给出了新的解决方法如下:
通过抽样给定模型h(r)和g(Δr)的参数,对于h(r),通过前面的方法,应用最小二乘法求出对应的形状Xh;对于g(Δr),给定其中的参数后利用测试样本中的部首的形状就可以直接求出对应的形状Xg,对Xh和Xg进行匹配,然后对匹配后的Xh和Xg进行线性插值,就可以得到最后的形状,线性插值如下:

其中λ为参数,0≤λ≤1。
上面只考虑了测试样本中只有一个汉字包含要研究的部首的情况,若测试样本中还有一个汉字也包含要研究的部首,为此我们建立模型:

对于模型2.1,在极端情况下,当λ=0时,X=Xh,这对应于测试样本数为零的情况,此时部首完全由训练样本学习得到;当λ=1时,X=Xg,这对应于测试样不数非常大的情况,此时,可以通过直接学习测试样本来求得部首的模型,通过这个模型可以解决两个汉字包含要研究的部首的问题。
由各个部首组成单字的模型和由各个笔划组成部首的模型类似,包括部首模型和部首之间的相对大小和位置模型两部分,其中部首模型由上面表示,部首之间的相对大小和位置模型用KPCA表示.给定单字的统计模型以后,通过随机抽样就可以生成汉字。
2 实验
本文在HCL2000汉字数据库的基础之上用Mathlab数学软件进行实验,样本库来自于文献[5],它是三个人写的样本集。实验中使用高斯核,在研究笔划的形状时,取σ=5,在研究笔划之间的空间大小和位置关系以及部首之间的空间大小和位置关系时取σ=20。
本实验通过学习其中两个人的手写汉字,并且给出第三个人的手写汉字“把”,最后生成符合第三个人手写风格的汉字“把”,实验生成的图像如下:

图2 生成的汉字”把”
在上图中得到了符合一定风格的汉字,这证明了本文提出模型的有效性。
3 实验运行的源代码
下面是mathlab软件实验本文改进方法kpca的源代码:




4 总结和展望
本文研究了手写汉字自动生成的问题,建立了汉字的统计结构模型,再PCA和KPCA方法的基础上给出了笔划、部首和单字的统计模型,从而实现了汉字的生成,以后的工作主要包括形状度量的建立和最终生成汉字的评价函数的建立两个方面。
[1]Songhua Xu,F.C.M.Lau,W.K.Cheung,Yunhe Pan.Automatic generation of artistic chinese calligraphy[J].IEEE Intelligent Systems,2005,20(3).
[2]Kim I J,Kim J H.Statistical character structure modeling and its application to handwritten Chinese character recognition[J].IEEE Trans PAMI,2003,25(15).
[3]Cootes,Taylor,et al..Active shape models:their training and application[J].Computer Vision and Image Understanding,1995,16(1).
[4]Y.Rathi,S.Dambreville,A.Tannenbaum.Statistical shape analysis using kernel pca[J].In:SPIE,Electronic Imaging,2006.
[5]任俊玲,郭军.HCL2000手写汉字数据库的更新及相关研究[J].中文信息学报,2005(5).
[6]M.B.Stegmann,D.D.Gomez.A brief introduction to statistical shape analysis.tech.rep.,Richard Petersens.Plads:Building 321,DK-2800 Kgs.Lyngby,2002.
