基于Pspice的电路容差分析在储能放电电路中的应用

熊莉英 黎 恒

(西南科技大学 信息工程学院，四川 绵阳621010)

在电子设备研制与应用中，经常会遇到因元器件参数漂移导致电路性能变化，电路功能失效等问题，这些问题不仅延长设计周期，还增加维护成本，因此在电路设计过程中需引入电路容差分析来提高电路的可靠性。

电路容差分析是由日本质量管理专家田口玄一于20 世纪60 年代提出的，作为“三次设计”（系统设计、参数设计、容差设计）的一种重要分支，它大大提高了电路可靠性，保证了电路的输出一致性、降低了设计生产成本。电路容差分析就是建立电路性能关于电路元器件参数容差范围的数学模型， 分析器件参数容差对电路性能的影响情况，从而优化设计。

1 电路容差分析方法

国家军标GJB/89-97《电路容差分析指南》中指出，容差分析是一种预测电路性能参数稳定性的方法。 常用的分析方法有两种，一是以灵敏度为基础的方法， 如最坏情况分析法，（Worst-Case Analysis），它是一种非概率统计方法，分析在电路组成元器件参数最坏情况下的线路性能参数偏差，它利用已知元器件参数的变化极限来预计电力性能参数变化是否超过了允许范围。 在预计电路性能参数变化范围时，元器件参数的变化取上、下极限值，因此它得到的是电路性能指标最大偏差，最严格地决定了元件所能容许的误差，虽然实际生产中，这种情况出现的概率很小，是一种很保守的情况分析，但它对衡量产品质量非常有用，即通过了最坏情况分析的设计，电路可靠性最好，对航天、反应堆等风险较大设备的电路尤为适用。

第二种方法是以概率统计为基础的方法， 如蒙特卡洛分析法，它是当电路组成部分的参数服从某种分布时。 对其进行大量随机抽样，对电路进行仿真分析，计算电路性能参数的统计特性和偏差范围的一种统计分析方法。

不论哪种分析方法都需要建立具体电路的数学模型，不但计算复杂，工作量巨大，而且电路模型不能通用，因此限制了容差分析技术在工程实际中的应用。 随着EDA（Electronic Design Automation）技术的飞速发展，出现了许多电子系统仿真软件，在这些软件上进行电路容差分析，可避免传统容差分析计算量大，参数调整缺乏灵活性等问题。在众多EDA 软件中，OrCAD 公司的Pspice 软件因其专业性强、 计算精度高、仿真结果合理等特点，使得在其基础上的电路容差分析具有更好的实用意义。

2 某装置储能放电单元电路指标分析

图1 储能放电单元电路模型

某装置中储能放电单元是其重要环节， 要求具备较高的可靠性，其电路模型如图1 所示，其中C 为储能电容，L 为放电回路总电感（包括电容器电感、传输线电感和负载电感），R 是放电回路等效电阻。 当该单元电路元器件参数发生偏差时，可能导致放电电流周期和幅值发生改变，从而使得某装置无法实现既定功能。 因此需研究各元件参数的偏差对电路性能的影响情况，并在保证放电电流周期和幅值的满足要求的前提下合理选择元件的偏差范围降低产品成本。

针对图1 电路放电电流周期T 和幅值IM两大指标分析如下，其放电电流的周期T 为：

可知放电电流周期T 只与电路中L 和C 参数相关，与R 无关，且L 和C 参数越小，放电周期就越小。

又据电路方程计算放电电流如下所述。

将式（2）对时间t 微分，得:

式（4）中:

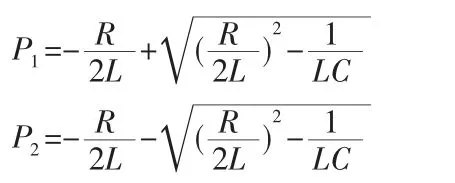
式（6）中：

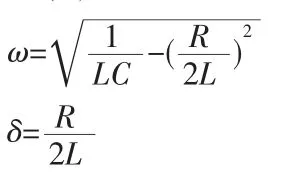
3 电路容差分析的Pspice 实现

系统对储能放电单元的性能参数要求为： 当电容C 储能电压稳定在2.0kV 时，放电电流周期要小于3.5μs ，放电电流第一峰值绝对值应大于等于3.0kA。 初始选择电路元件参数值及偏差如表1 所示。

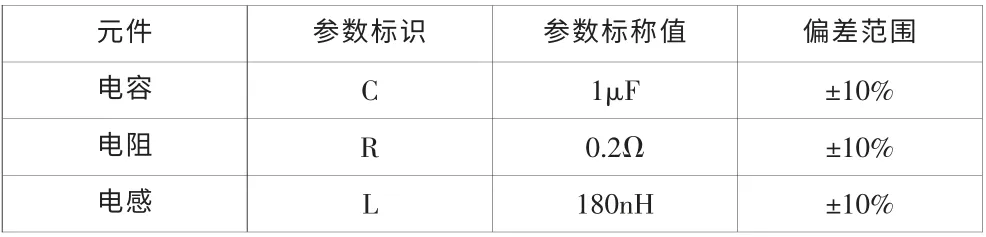
表1 电路元件参数及偏差值

为了保证设备的可靠性，在Pspice 中选用最坏情况分析。 设置电容C 的充电电压U0=2000kV，在设定偏差为±10%的情况下，对放电电流幅值及周期分别进行瞬态响应仿真， 仿真曲线如图2 及图3 所示。其中曲线1 为无偏差时情况，曲线2 为最坏情况曲线。

图2 无偏差和偏差为±10%时电流幅值IM 仿真曲线

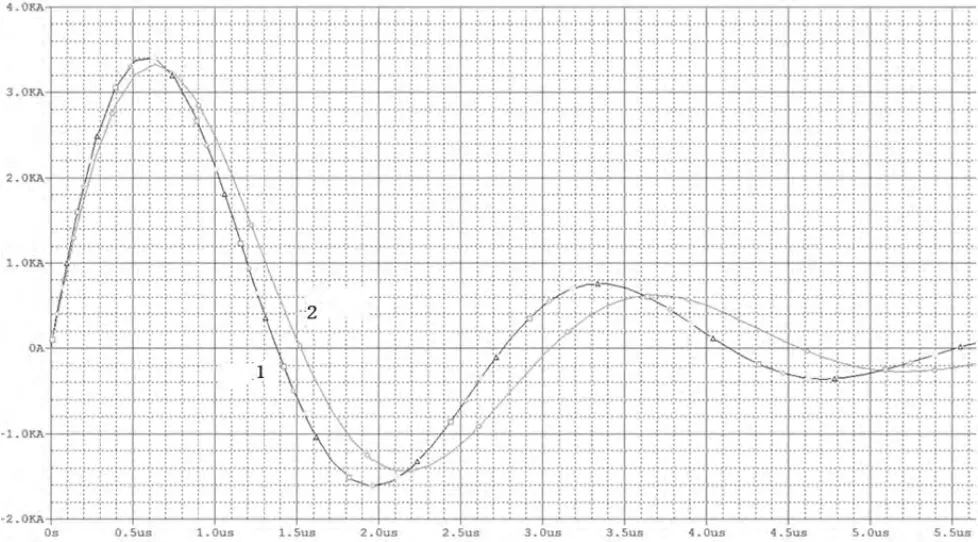
图3 无偏差和偏差为±10%电流周期T 仿真曲线

由仿真曲线可知，结果满足要求。

为了得到更好的经济指标，放宽器件的偏差要求，可继续将表1中的偏差范围取值为±11%或更大来进行仿真研究。 当偏差范围取值为±11%、±12%时， 系统仍然满足指标要求， 但当偏差范围取值为±13%时，电流幅值的仿真曲线为图4 所示，同样曲线1 为无偏差时情况，曲线2 为最坏情况曲线。

图4 无偏差和偏差为±13%电流幅值IM 仿真曲线

由图4 可知，在偏差取值为±13%时，电流幅值几乎小于3.0kA，电路可靠性不够，因此，选择元器件参数偏差为±12%，是经济指标和可靠性指标都较好的偏差范围。

4 结论

对某储能放电电路应用Pspice 进行最坏情况分析，显示该放电单元电路元器件参数偏差选为±12%的条件下， 放电电流周期和幅值均能满足电路性能指标要求，为实际生产提供了理论依据，节省了设计时间，扩大了器件选型范围，降低了电路成本。

［1］石永山，王飞，刘铭.电路容差分析在设计中的应用[J].光电技术应用，2010,12.

［2］杨华中.电子电路中的计算机辅助分析与设计方法[M].清华大学出版社，2008.

［3］李慧贞.基于EDA 技术的电路容差分析在电路设计中的应用[J].陕西科技大学学报，2010,7.

［4］牛晓春，郭利强，于天朋，何榧.容差分析技术在炮射导弹电路中的工程应用[J].国防技术基础，2009,11.