蒙特卡洛方法在战时车辆装备完好率计算中的应用

张忠义，龚 正，周 翔

(蚌埠汽车士官学校 运输勤务系，安徽 蚌埠233011)

汽车部(分)队担负着作战后勤运输保障的重要任务，而战时车辆的保障能力和维修水平是决定着后勤运输能力高低的一个重要指标。本文运用蒙特卡洛方法进行车辆装备完好率的建模研究，通过仿真方法可预先得到车辆完好率，以期对车辆战时完好率进行科学预测和随机评判。

1 战时车辆维修保障系统简介

按照部队有关车辆维修管理规定，目前的维修机构设置为3 级，分别为基层级、中继级和基地级保障机构，其相应承担不同的修理级别和任务。在与3 级维修机构的交换流通过程中，车辆作为间歇使用的系统，其遂行任务时间和作战消耗损伤的修复时间都与维修机构的保障能力、资源数量等因素发生交换关系，在这种交换关系中车辆的状态也会不断转移(如图1 所示)。在交换过程中，车辆各个需要维修的部件、总成作为子系统，也在不同级别的机构间流动，系统的最终目标是车辆的修复完毕。

图1 车辆状态转移

战时完好车是指能够顺利执行运输保障任务而不出现故障或影响使用的机械性破坏的车辆，完好车数与实有车数的比值(记为P)称为车辆的完好率，完好率的高低对于赢得战斗至关重要。

在战时某一阶段，车辆是否处于完好状态，其主要决定因素是维修保障工作的频率和时间长短，而维修保障机构遂行保障任务的能力和效率则主要取决于2 个方面:一是车辆本身的技术状况和战损程度;二是各级维修保障机构资源的配置及自身管理运行状况。同时，战时车辆使用是系统进入维修状态的直接动因，在建模之前，可以把车辆的维修保障活动视作一个“投入—产出”的过程。在这个过程中，维修保障人员时间、维修保障资源消耗为“投入”，车辆由故障车或战损车恢复为完好车则为“产出”，车辆完好率模型在这一前提下建立。

2 建模与算法

2.1 蒙特卡洛方法

蒙特卡洛方法亦称为概率模拟方法，也称为随机抽样技术或统计试验方法。它是通过随机变量的统计试验、随机模拟来求解工程技术问题的一种近似解方法。该方法解决问题的基本思想:①建立一个与所求解有关的概率模型，使所求解就是所建立模型的概率分布或数学期望;②对这个模型进行随机变量抽样观察，即产生随机变量;③用算术均值作为所求解的近似估计值［1］。

2.2 假设条件

在建立车辆装备完好率仿真模型之前，需要以下基本假设作为条件。

(1)车辆系统由5 个子系统构成，分别为发动机系统、电路系统、车载通信系统、供油系统和底盘系统。

(2)车辆由完好转为非完好的触发条件为战损或自身故障。

(3)车辆系统为串联系统，即车辆任意一个子系统未完成修复或任意一个维修级别没有完成工作，车辆的状态均为非完好。

(4)为便于仿真运算，车辆故障或战损类型为5 个子系统单独发生，不考虑子系统的并联故障。

(5)保障延误包括抢修急救时间、故障战损车辆后送、车材部件、保障设备以及维修人员延误等，本文将保障延误时间作为一个单独的随机变量考虑。

2.3 仿真模型

2.3.1 任务仿真

由于不同的作战等级和任务难度对应的任务步骤各不相同，在考虑任务仿真的过程中，忽略一些细节过程，简化任务事件数量，把车辆维修保障任务的几个关键环节抽象出来，进行简化设计，最终任务抽象为给基本任务分配装备、任务前准备、任务开始、任务执行、任务返回几个事件。任务返回时间取决于车辆的故障情况和战损程度。如果车辆在任务执行过程中没有发生故障或没有遭到袭击，按照正常执行任务完毕时间返回;如果车辆发生故障或遭到战损，则在故障或损伤发生时刻返回。

2.3.2 系统故障仿真

军用车辆发动机系统、电路系统、车载通信系统、供油系统和底盘系统中任一系统设备故障，都将导致车辆系统处于不能完成运输保障任务的状态，即非完好状态。车辆某一子系统或部件能正常使用的时间(寿命)一般服从某一概率分布函数，根据机械和电子领域常用的分布函数，各系统的分布密度如下。

(1)由于发动机系统、车载通信系统、供油系统和底盘系统多由机械类设备构成，或者其损坏原因多为机械损坏，故可采用机械类系统故障的分布函数，即威布尔分布，其可靠度分布密度为

式中:n为形态参数;t0为尺寸参数。

可靠度函数为

(2)电路系统多由电子设备构成，车辆电路系统可采用电子系统故障的分布函数，即指数分布，其可靠度分布密度为

式中λ为故障率。可靠度函数为

战时车辆非完好状态表现形式为故障或战损，车辆子系统由于自身不可靠而导致的故障比例为，因战损而导致的故障比例为βi

(3)车辆系统的可靠度分布函数为

式中fi(t)(i=1，2，…，5)为5 个子系统的可靠度分布密度函数。

2.3.3 维修保障仿真

维修保障仿真包括车辆日常维护仿真和修复性维修仿真。车辆日常维护主要包括出车前后检查、日常保养、定期检查等工作。车辆日常维护过程按照《车辆保养规定》来执行。车辆使用过程中发现故障后需要进行修复性维修，其主要目的是排除故障，将车辆由非完好状态转换为完好状态。这种类型的维修活动发生的时机、地点和执行维修作业的时间都具有不确定性。当车辆某一个子系统发生故障时，第一步是在基层级维修机构检测并排除故障，若由于本级的故障检测能力和修理能力的制约不能完成修复任务，则需将故障件送入中继级或基地级进行修复。由于不同修理级别配属的维修力量和资源不同，其对车辆的修复时间也会不同，可以通过对多个维修机构的实际数据采样并进行统计分析，得出故障子系统在某一维修保障级别能修复的概率，从而确定修复性维修工作地点。在仿真过程中，设第i个子系统发生故障在第1 级(基层级)维修的比例为γi1，在第2 级(中继级)维修的比例为γi2，在第3 级(基地级)维修的比例为γi3，且∑3j=1γij=1。车辆修复性维修停用模型如图2 所示。

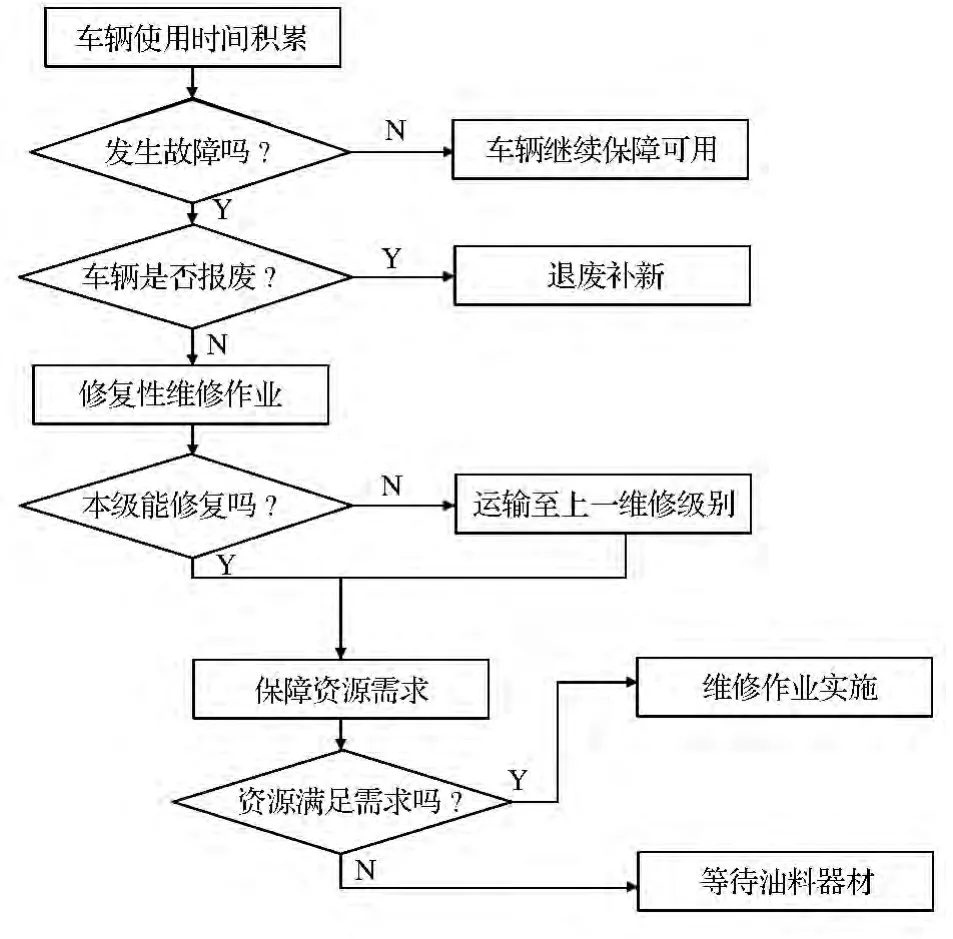
图2 维修停用模型

(1)系统修复时间。根据排队论原理，系统维修过程实质上类似于一个排队系统，车辆或其子系统发生不同类型的故障或损伤，则自动转入相应的维修队列，按故障系统优先级或先进先出的规则依次进行维修。故障车辆在维修队列中接受“服务”的时间分为维修保障延误时间和故障诊断修复时间2 个部分。根据常用故障修复模型惯例，故障修复时间服从指数分布。通过指数分布逆变换可在仿真过程中计算修复时间［2］。

(2)维修保障延误时间。指系统排队进出的总时间除去故障修复时间以外的所有时间。维修保障延误时间内车辆的状态依然是非完好。将维修保障延误时间作为一个单独的变量，根据惯例，其服从对数正态分布，维修保障延误时间的抽样TL为

式中:μ和σ为统计获得的对数正态分布参数;η1和η2为随机变量。

2.4 仿真计算

根据所建模型，应用Monte.Carlo 仿真方法，通过离散分布概率抽样技术实现车辆维修保障过程的随机过程［3］。

(1)将车辆技术状况、维修性能、日常管理情况等作为输入数据。

(2)仿真计算中，战损引起的故障为考虑前提，选取0 ～1 的随机数μ1，如果μ1小于战损率，则认为故障是由战损引起，反之则判定故障是由车辆自身技术状况不良引起。

(3)选取0 ～1 随机数μ2，根据μ2来判定战损的子系统:如μ2∈(0，β1)，则为发动机系统;如，则为电路系统;如则为车载通信系统;如，则为供油系统;如，则为底盘系统。

(4)如果μ1大于战损率，则考虑系统自身引发的故障。抽取0 ～1 随机数μ3，如果μ3大于车辆自身的可靠度，可判定车辆的非完好状态是由系统自身引起。

(5)选取0 ～1 随机数μ3，根据μ3来判定故障的子系统:如μ3∈(0，αi］，则为发动机系统;如，则为 电路 系统;如，则为车载通信系统;如则为供油系统;如，则为底盘系统。

(6)车辆任一子系统发生故障，即转入维修状态。可选取0 ～1 随机数μ5来确定故障子系统的维修机构:如μ5∈(0，γ21］，则在基层级维修机构;如μ5∈(γ21，γ21+γ22］，则在中继级维修机构;如μ5∈(γ21+γ22，1］，则在基地级维修机构。

(7)由相应维修机构点的指数分布逆变换可产生维修时间，按照对数正态分布抽样获取保障延误时间TL，2 个时间之和即为维修停用时间。

(8)车辆当天完好率的命令语句为

P=M/D(完好率为当天完好车辆数与仿真初始执行运输保障任务的车辆总数的比值)

3 仿真案例实验

3.1 数据设置

假设由100 台车辆组成的车队在执行运输保障任务，任务持续时间为10 d，任务保障频率为1次/(车·d)，每车次的行驶时间为5 h，仿真间隔时间设置为1 d(24 h)。定义战损率为每千车次战损的车辆数量，设前2 天的战损率为30/(千车·次)，3—6 天的战损率为50/(千车·次)，7—10 天为70/(千车·次)。在该假设中，车辆自身故障比例α、战损比例β和各级维修站点的维修比例r见表1。车辆各子系统使用时间(寿命)威布尔参数值见表2。各级维修站点平均维修值MTTR和保障延误时间分布参数值见表3。

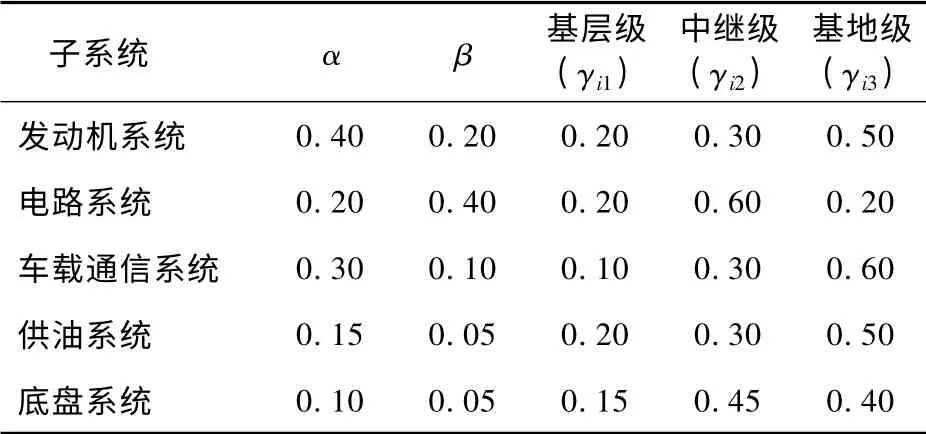
表1 车辆系统功能结构分解及α、β、γ 值

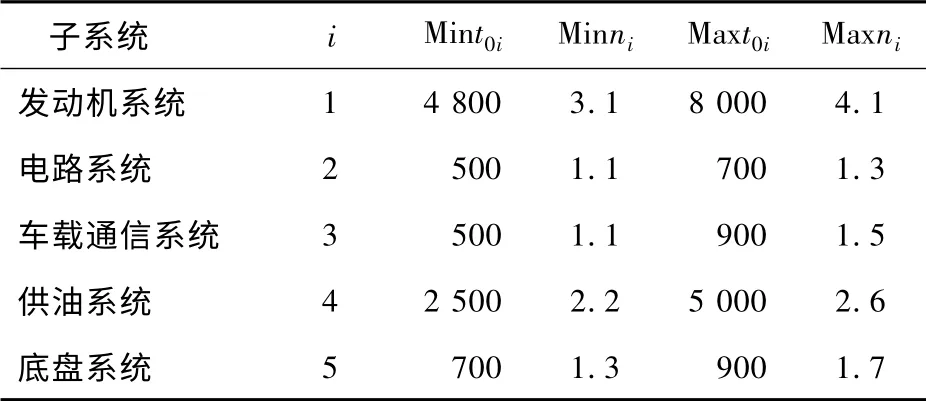
表2 各子系统威布尔参数值

表3 各维修站点平均维修值和保障延误时间分布参数值

3.2 仿真输出

图3—6 给出了车辆完好率变化曲线，表4 给出了第2、6、7、10 天的车辆装备完好率［4］。

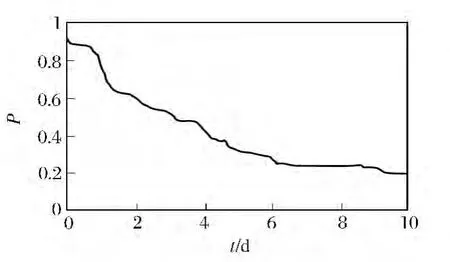
图3 威布尔参数为Min、MTTR 为B

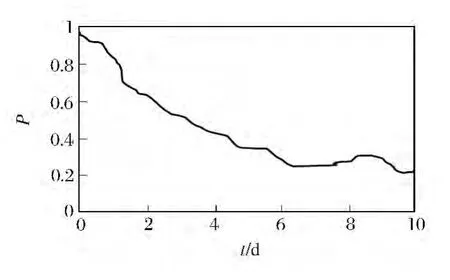
图4 威布尔参数为Max、MTTR 为B

图5 威布尔参数为Min、MTTR为A

图6 威布尔参数为Max、MTTR 为A

表4 车辆完好率

3.3 数据分析

从仿真输出图像可以看出，在遂行运输保障任务过程中，即使有各级维修机构的存在，但是车辆的总体完好率还是在逐渐下降的，排队系统中的修复作业和油料器材等待等是导致曲线波动的主要因素。图3 显示出运输保障任务完成后车辆的完好率只有初始状态的26%。图4 的仿真输出表明在改善车辆初始技术状态后，任务完成时车辆完好率提高3%。从图5 可以看出，在改善维修水平后，车辆完好率在任务完成后为27%。图6则反映出在改善了车辆初始状态性能和提高维修机构工作能力后，任务完成后车辆完好率可达到42%。

4 结 语

战时汽车部(分)队的车辆使用和管理效能高低的直接反应形式就是车辆的完好率，通过使用装备完好率研究领域的常用模型——蒙特卡洛算法，可以仿真计算战时车辆的完好率。仿真输出数据具有较高的参考价值和指导作用，能对汽车部(分)队战时的车辆使用和维修提供理论指导。通过对影响因素的分析，可以引导车辆和保障装备设计人员、使用管理和维修人员改进保障和维修方案，使军用车辆的战备率和完好率得到进一步提高。

［1］ 杨春，李本威.基于蒙特卡洛法的飞机装备完好率建模仿真［J］.航空计算技术，2010(9):71-72.

［2］ 韩维，李成.基于Markov 模型的机群完好率研究［J］. 飞机设计，2011(8):61-62.

［3］ 范英飙，王进才.装备维修保障与失效因素分析［J］.中国科技博览，2010(3):76-77.

［4］ 陈永胜.基于MATLAB 的混沌系统仿真［J］. 廊坊师范学院学报:自然科学版，2013(5):9-11.