基于动态窗口的轮廓查询技术研究

许兴义 陶明慧

（中国人民解放军西藏77635 部队，西藏 错那856700）

1 轮廓查询技术研究现状

空间数据库系统是描述、存储和处理空间数据及其属性数据的数据库系统。空间数据库是随着GIS 的开发和应用而发展起来的数据库新技术。它不是独立存在的系统，而是与应用紧密结合，通常是GIS 的核心。 空间查询优化是空间数据库相关技术研究的难点和突破点，轮廓查询技术已经成为空间查询及优化领域的热点课题。 “轮廓”（Skyline）这个概念最初是2001 年Borzsonyi 等人在VLDB（Very Large Databases）会议上作为一个操作被提出来的。 由于轮廓查询技术有着重要的理论研究价值和实际应用价值，所以一直是相关领域专家们的研究重点。 下面分别介绍国内外的研究成果。

D＆C （Divide-and-Conquer） 分治轮廓查询方法[1]，2001 年ICDE（Interational Conference on Data Engineering）会议上，Borzsonyi 等人提出。 该方法将数据集划分成多个分区，然后利用主存算法来分别计算每个分区内的局部轮廓，最终的轮廓通过将局部轮廓筛选并获得。 该方法仅对小数据集有效。因为，如果整个数据集符合内存大小，那么仅需要应用一次主存轮廓算法即可。 对于大数据集，分区的过程就需要至少一次读和写整个数据集，因此，导致严重的I/O 代价。 这种方法不适合在线处理，因为它不能在分区阶段完成之前返回任何轮廓点。

BNL （Block Nested Loop） 块嵌套循环轮廓查询方法[1]，2001 年ICDE 会议上，Borzsonyi 等人提出。这种方法就是基于这个思想扫描数据文件，在主存中保存一个轮廓点的候选列表，开始的时候列表中包含第一个数据点，随后的点p 分3 种情况：

（1）如果p 被表中的任何一个点支配，那么p 会被删除，它不是轮廓的一部分。

（2）如果p 支配列表中的任何点，那么p 将被插入列表中，并且列表中所有被p 支配的点都将被删除。

（3）如果p 既不被支配，也不支配列表中的点，那么它将被插入到列表中，它有可能是轮廓的一部分。

BNL 的一个问题就是列表可能变得比主存还要大，当这种情况发生时，所有溢出的数据点都被添加到一个临时文件中，这就需要多次执行BNL。 BNL 的优点就是它广泛的应用性，因为它无需索引或将数据文件排序就可以应用到任意维上。BNL 的主要问题就是对主存的依赖和在渐进处理方面存在缺陷。

位图轮廓查询方法（Bitmap）[2]，2001 年VLDB 会议上，Tan 等人提出。 将所有的信息在位图中编码来确定一个点是否在轮廓上。 位图法的效率依赖于位图操作的速度。 这个轮廓的计算是昂贵的，因为对于每一个要检测的数据点，必须检索所有点的位图来得到对应位。 如果不同值的数目非常大，那么，空间代价可能会很高。而且这种方法不适合动态数据集。

NN（Nearest Neighbor）最近邻轮廓查询方法[3]，2002 年VLDB 会议上，Donald Kossmann 等人提出。 它利用最近邻查询的结果来递归划分数据空间，分别求得轮廓。最近邻方法的查询速度比前几种方法都快，但是对于高维数据来说，该方法存在严重的空间重合问题。

SFS（Sort Filter Shyline）排序过滤轮廓查询方法，2003 年ICDE 会议上，Chomicki 等人提出了BNL 的改进方法。 根据一个优先选择函数首先对整个数据集进行排序， 候选点按照分值以升序插入到列表中，因为具有低分值的点可以支配大量的点，因此，使得修剪更有效。 SFS展现出渐进的特点，因为数据的预排序能够确保支配点p’的点p 必须在p’之前被访问，因此，能够立即将插入到列表中的点作为轮廓点进行输出。然而SFS 不得不扫描整个数据文件才能返回一个完整的轮廓。

BBS（Branch and Bound Skyline）分支限界轮廓查询方法，2005 年TODS（Transactions on Database Systems）会议上，D.Papadias 等人提出。它与前面的最近邻轮廓查询方法类似，采用分支限界矩形图，通过深度优先遍历算法来进行轮廓查询，该方法没有考虑到用户后期筛选计算的方便性，缺少一定的实际应用性，不能很好地满足用户的需求。

以上几种轮廓查询技术的比较如表1 所示。

表1 几种轮廓查询技术的比较

基于以上分析， 本论文将采用基于动态窗口的轮廓查询技术，可以较好解决以上查询方法存在的缺陷。

2 动态窗口轮廓查询技术

2.1 空间数据库轮廓查询示例

在d 维空间中，轮廓是一个d 维点的集合，点集合是由在所有维上不被其它任何一个点支配的点组成。 假定一个点的集合P1，P2，…，Ps， 点Pi支配点Pj当且仅当点Pi在任意轴上的坐标都不大于点Pj对应的坐标。 查询结果返回所有的点Pm，Pm是不被任一个Pn支配的点。

轮廓在涉及多标准决策的应用中起着非常重要的作用。 例如，在出行选择交通工具时，有火车和飞机可供选择，可是飞机价格比火车票贵一些，但乘坐火车花费路途时间又太长，如何选择适合自己最佳的方案，轮廓的计算可有效解决这样的问题。 如图1 所示：

图1 轮廓的示例

用x 轴来表示乘坐交通工具的价格，用y 轴来表示路途花费的时间，两个坐标轴表示的事物不同，所以单位尺度表示的意义也不同。坐标系中的点表示花费的时间。

点a,b,c 是最优候选集，这3 个点不被空间中任何其它对象支配，其它的点相对这3 个点不是费时长就是价格高或者二者都有，都不理想。 点a 时间相对来说长，有最长的时间但是价格低，点b 时间相对a来说短一些，但是价格相对高一些，点c 价格最高，但花时最少，根据用户自己的实际情况可选择不同的出行方式。

2.2 基于动态窗口查询的轮廓查询算法

2.2.1 算法思想[4-10]

基于动态窗口查询的轮廓查询算法通过窗口查询q 来访问所有轮廓点集合中的点，是将单个轮廓查询转换为多个不同的动态窗口查询，只有查询窗口的右边界是移动的。 查询窗口不断变化来缩小查询空间，访问有可能是轮廓上的点，并且每个数据点只访问一次。不用访问空间对象集合中的全部数据点。

如图2 所示，N1，N2是空间中的两个最小边界矩形（Minimum Bounding Rectangle，MBR），MBR 是用来界定地图大小的，确保要查询的空间信息都在该范围内，MBR 可人为设定，一般以地图的左下角和右上角标注。 首先生成一个查询窗口q，窗口的长q.length 是与y 轴距离最近的MBR 到y 轴的距离，即q.length=|0F|(0 是原点)，其宽q.width是与x 轴距离最远的MBR 到x 轴的距离，即q.width=|AF|。搜索到点a和h 在查询窗口q 中，因为在查询窗口内只有空间数据点a 和h，没有其它的点的横坐标小于点a 和h，且h 的纵坐标小于a 的纵坐标，所以点h 支配点a,点h 是轮廓点的点。 点h 支配矩形ABCD 内的数据点，因此矩形ABCD 内的所有点肯定不是轮廓中的点，有可能成为轮廓中的点的数据点必定在矩形DCEF 内，下一步就不必对矩形ABCD 进行搜索了，只要对矩形DCEF 进行搜索即可。 那么就以点h(点D)为查询窗口的一个顶点对矩形DCEF 进行搜索，采用相同的方法不断修剪查询空间。

图2 轮廓查询分析

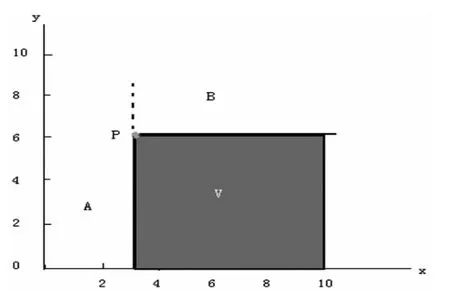
图3 查询的有效区域

对于每一个查询到的轮廓上的点p 来说，都对应着一个有效区域V，这个有效区域V 就是以点p 为左上角顶点的区域。 如图3 所示，点p 是刚查询到的轮廓点，阴影区就是点p 对应的有效区，接下来要查找的轮廓点都在这个有效区V 内。 因为区域A 内的空间数据点已经经过查询判断，区域B 内的点全部被点p 支配，所以只有区域V 是轮廓点所在的区域。 这样就只对这点p 的有效区进行查询，不必对整个空间进行查询。

2.2.2 算法描述

算法说明和分析中用到的符号表示如下：

S 表示空间数据点集；p 表示空间数据点集s 中的数据点；L 表示轮廓列表；Li表示轮廓列表中第i 个轮廓点；Pn表示第n 个查询窗口；VU表示查询窗口上边界的速率；VB表示查询窗口下边界的速率，VR表示查询窗口右边界的速率；N 表示MBR 构成的中间结点；q.length表示查询窗口q 的长度；q.width 表示查询窗口q 的宽度；p.x 表示数据点p 的x 坐标；p.y 表示数据点p 的x 坐标和y 坐标。

基于动态窗口查询的轮廓查询算法具体描述如下[11]：

输入：空间数据点集S

输出：轮廓点集L 及其对应的查询窗口

Begin

Step1:L=Φ;VU=0; VB=0;VL=0;VR=1;

q1.length=0;

q1.width=Maxdist_x(Ni);

n=1;

Step2:while q 的右边界没有到达所有MBR 的右边界do

If N 与q 相交then

{将N 中落入q 中的点进行比较，y 轴坐标最小的点Pi插入L 中，Li=Pi;

以点Pi为查询窗口的左上顶点，且n=n+1;

Qn.length=0; Qnwidth=‖Pi.y‖ ;

IfPi.y=Pi.y(i＜j) then

Pj从列表中删除；}

Return(Li, qn);

Return(Li, qn);

End while

End

2.2.3 算法分析

基于动态窗口查询的轮廓查询算法将单个轮廓查询转换为多个不同的动态窗口查询，只有查询窗口的右边界是移动的，其他边界都是静止的。 算法仅需要对有效区内的空间数据点进行查询，无须对整个空间的数据点进行搜索查询，有效地减少了查询空间，被访问点的数量明显减少。

查询窗口只访问轮廓点和与轮廓点具有部分相同坐标的点，并且每个数据点只访问一次。 被查询窗口检索到数据点不一定就是轮廓点，需要根据其坐标情况进一步的判断才行。 被检索到的数据点主要有下面3 种情况：

1）有多个数据点同时落入查询窗口中，即这些数据点具有相同的x 坐标。 如图4 所示。

图4 情况1 多个数据点落入查询窗口

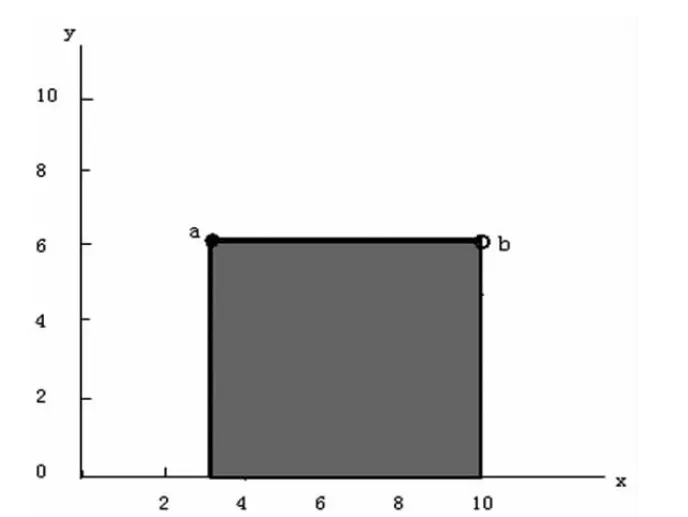
图5 情况2 落入查询窗口的数据点与轮廓点部分坐标相等

2）新落入窗口的数据点与上一个插入到轮廓列表L 中的轮廓点具有相同的y 坐标，根据轮廓的支配定义可知，新点被支配，不是轮廓点，所以将新点删除。 如图5 所示。

3）落入查询窗口但又不满足前两个条件的数据点肯定是轮廓上的点，将其加入轮廓列表L 中。

3 基于动态窗口轮廓查询技术设计与实现

下面举例对基于动态窗口查询的轮廓查询算法对人员管理信息系统中的数据对象（静态数据对象）进行轮廓查询，详细分析并说明其具体查询过程。

假设有空间数据点集S，S={a,b,c,d,e,f,g,h,i}，空间数据点的坐标分别 为a(1,9)，b(2,10)，c(4,8)，d(6,7)，e(10,8)，f(7,5)，g(5,6)，h(4,4)，i(3,2)，j(10,4)，k(9,1)，m(6,2)，n(8,3)分 别 表 示 流 动 人 员 暂 住 地、流 动 人 员 工 作地、发现流动人员位置、执法人员固定执勤点、发现大量流动人员位置、执法人员流动执勤点、临检人员、临检固定点、临检发现流动人员处、执法单位驻地、地方政府所在位置、临检流动点，如图6 所示。

根据这些点，生成其MBR 如图7 所示。

图6 空间数据

图7 MBR

假设所有空间数据点都在坐标系的第一象限中，建立坐标系。 设轮廓点集为L，查询过程：首先轮廓点集L 设为Φ，生成一个查询窗口q，查询窗口的一个顶点在原点0，其长q.length 是与y 轴距离最近的MBR 到y 轴的距离，其宽q.width 是与x 轴距离最远的MBR 到x 轴的距离， 如图8 所示。 当前检索到点a 落在查询窗口内， 将点a 插入L中，L={a}即首先检索到的是流动人员暂住地，并成为首个轮廓点。

图8 L={a}

然后查询窗口q 改为以点a 为一顶点， 其宽q.width 是-‖a.y‖,其中‖a.y‖表示点a 到x 轴的距离， 负号表示y 轴负方向的长度，这样点a 是查询窗口的左上角顶点。 相反，正号表示y 轴正方向的长度，那么点a 就是查询窗口的左下角顶点。 查询窗口q 的长q.length 由0开始不断增加，直到查询到中间输入，并且有空间点落入查询窗口中。如图9 所示，点i 落入查询窗口，i.y≠a.y，则将点i 插入L 中，L={a，i}即临检发现流动人员处成为轮廓点。

图9 L={a,i}

接着，查询窗口q 改为以点i 为一顶点，其宽q.width 是-‖i.y‖，其长q.length 由0 开始不断增加，直到有空间点落入查询窗口中。 如图10 所示，点m 落入查询窗口，m.y=i.y，因为点m 被点i 支配，则点m不插入到L 中，所以L={a,i}。

图10 L={a,i}

图11 L={a,i,k}

继续查询窗口q 改为以点m 为一顶点，其宽q.width 是-‖m.y‖,其长q.length 由0 开始不断增加，直到把空间点落入查询窗口中。 如图11 所示，点k 落入q 中，k.y=i.y，将点k 插入L 中，L={a,i,k}即地方政府所在位置成为第3 个轮廓点。

按照上面的方法继续执行，当查询窗口到达MBR 的右边界时，结束查询。 如图12 所示，查询结束，最终结果L={a,i,k}。

图13 是查询所得的轮廓，轮廓上有数据点a,i,k 即流动人员暂住地、 临检发现流动人员处和地方政府所在位置3 个空间位置为轮廓点。

图12 L={a,i,k}

图13 查询所得的轮廓

综上所述，窗口查询扫过的区域如图14 阴影部分所示，空间直线右上侧的点不在查询范围内， 所以在查询过程中不必对它们进行访问，从而大大减少结点访问数。

图14 查询区域

［1］BorzsonyiS,KossmannD,StockerK.The Sky line Operator[C]. ICDE, 2001.

［2］Tan K, Eng P,Ooi B,Efficient Progressive Skyline Computation[C].VLDB,2001.

［3］Kossmann D,Ramsak F,Rost S.Shooting Stars in the Sky: an Online Algorit -hm for Skyline Queries[C].VLDB,2002.

［4］Yu Jing, Liu Xin,Liu Guo-hua.A Window-based Algorithm for Skyline Queri -es[J].Computer Society,2005,9.

［5］Stojmenovic I,MiyakawaM.An Optimal Parallel Algorithm for Solving the Maximal Elements Problem in thePlane[J].Parallel Computing,1988,7.

［6］Matousek J.Computing Dominances in En [C]//information Pro-cessing Letters,1991,38.

［7］Roussopoulos N,Kelly S,Vincent F.Nearest Neighbor Queries[C].SIGMOD,1995.

［8］HjaltasonG,SametH.DistanceBrowsinginSpatialDatabases[C].ACMTODS,1999,24.

［9］Kossmann D Rost S Rost S.Shooting Stars in the Sky:an Online Algorithm for Skyline Queries[C].VLDB,2002.

［10］Wang Wei-ping,Li Jian-zhong,Zhang Dong-dong,Guo Long-jiang.Sliding Wi -ndow Based Method for Processing Continuous J-A Queries on Data Streams[J].Journal of Software,April 2006.

［11］刘国华,等.数据库新理论、方法及技术导论[M].电子工业出版社,2006.