基于突变理论与梯形模糊数的海洋视景仿真逼真度综合评定

梁洪涛，康凤举，翟楠楠

(西北工业大学航海学院，陕西西安710072)

视景仿真技术已经广泛应用于军事、工业、教育和其他领域［1-4］，特别在军用仿真中具有重要的作用，利用视景仿真技术对于军事作战人员在模拟训练中熟悉战场环境、掌握武器装备、提高作战决策能力有不可替代的作用.近几年国内外学者对逼真度理论研究也不断深入，模型或仿真的逼真度是由多维度量根据逼真度参照物来定性和定量测量的，是模型或仿真本质的属性.

在视景仿真逼真度指标体系及评定方法研究中，虽然研究者对视景仿真评估指标进行了初步划分和扩展［5-6］，但还没有形成一个标准、科学的逼真度指标体系;评估方法主要集中在层次分析法［7］、模糊评价法［8］、灰色关联方法［9］等多属性决策方法，这些方法利用自身特点从不同角度对多属性决策进行评价，但确定指标权重时，主观因素考虑较重，导致评判结果往往产生误差，影响最终决策.

文中将突变理论与梯形模糊数相结合，对3个典型海洋战场视景仿真逼真度系统进行综合评判.利用梯形模糊数方法对底层指标进行初始模糊隶属函数分析，根据突变模型的归一化公式进行量化计算，最后根据最终突变隶属函数值实现动态综合评判.

1 突变模型及其特性

突变理论是法国数学家托姆(Rene Thom)在1972年提出的一门现代新兴数学分支，是关于系统状态变量特征对控制变量依从关系的数学理论.该理论综合运用奇点理论、拓扑等价、结构稳定性、势函数与剖分引理等来研究自然界和社会现象中的多种形态、结构的非连续突变.

任何一个系统，其状态总要保持平衡，系统由一个平衡状态跃迁到另一个平衡状态时，即发生了突变，该过程的全貌可通过一个光滑的平衡曲面来描述.千差万别的突变现象，以其平衡曲面来分类.按照托姆突变理论分类定理，证明了渐变的控制因素(控制空间)所产生的突变行为(状态空间)，在控制空间不超过4维、状态空间不超过1维时，各种突变模型及特征如表1所示.

表1 突变模型及其特性

表1中后3列具体内涵如下:

1)势函数V(x)表示突变系统中状态变量和控制变量之间的关系，其中u，v，w，t为系统的控制变量，x为系统的状态变量，可以得到反映状态变量与控制变量间分解形式的分歧集方程.

2)平衡曲面方程M表示对于突变模型势函数V(x)的所有临界点集合.令V'(x)=0得到该平衡曲面方程，令V″(x)=0得该平衡曲面的奇点集，由V'(x)=0和V″(x)=0联立消去x，则得到系统的分歧集方程，它是突变理论的核心，各控制变量满足此方程时系统就会发生突变.

3)归一化方程由分解形式的分歧集方程导出，它将系统内部指标不同的质态归化为可比较的同一种质态，利用其对系统进行递归运算，求出各控制变量的突变值，最终获得表征系统状态特征的总突变隶属函数值.

2 梯形模糊数数据处理技术

三角形模糊数［10］已经应用于多指标系统评定，并取得了较好效果.但三角模糊数的相对最可能值仅是一个点值，对于大量存在的峰值较为扁平的量化分布，应用三角模糊数可能带来较大的模拟误差.针对这一问题，梯形模糊数却能通过“大概在某一范围，且最有可能在其中某一区间”的判定给予很好的解决［11］.

梯形模糊数的隶属度函数由4元组数来表示，如图1所示.

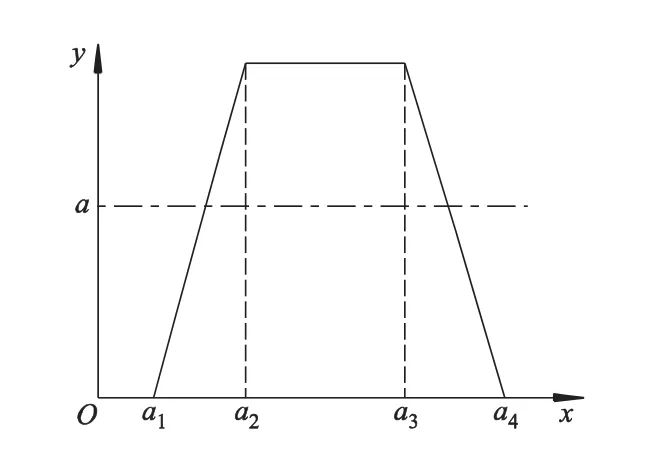
图1 梯形模糊数示意图

A=(a1，a2，a3，a4)，其中a1，a2，a3，a4为实数，且a1≤a2≤a3≤a4，它们之间的对应关系如下:

假设对某一个指标的模糊数的隶属函数为

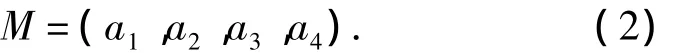
定量化计算采用α-截集技术，通过定义在α-截集的置信度区间，将梯形模糊数A转化为与一定可信度水平相对应的区间数进行计算，即

其中Aα为A的α-截集，它实际上是一个以α为自变量且可信度水平不低于α的数据集合.

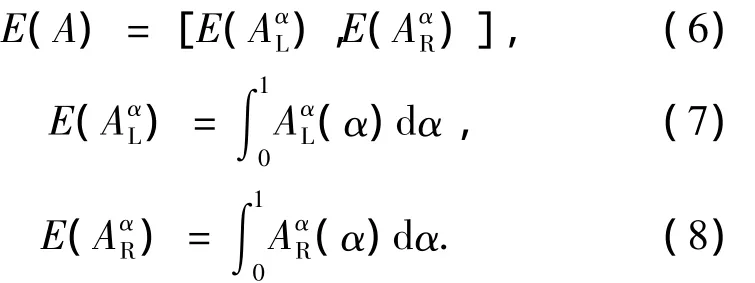
梯形模糊数的期望用期望区间的中值表示为

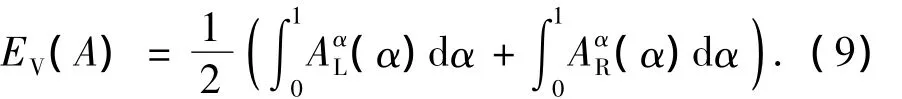
为减小个别专家的意见对权重结果的影响，提高评价结果可靠性，待选对象的最终评价结果通过多个专家意见加权来表示，即

对每一个指标计算出其多个专家加权信息即可以看作指标的初始隶属函数值，即

通过以上分析可知，可利用梯形模糊数对控制变量进行标准化，并计算其初始模糊隶属函数值.

3 基于梯形模糊数的突变决策方法

利用突变理论进行模糊综合分析与评判时，根据各个突变模型的归一化公式，并依照“非互补”或“互补”原则算出各层状态变量值，以蝴蝶型为例进行说明.假若系统的各个控制变量之间不相互关联，则应遵循“非互补”原则，即控制变量对应的突变级数值x值为xu，xv，xw，xt中最小值，即

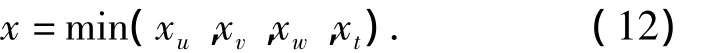
假若一个系统的控制变量之间存在明显的相互关联作用，则应遵循“互补”原则，即取诸控制变量相应的突变级数值平均值作为系统的x值，即

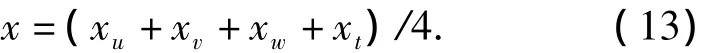
只有遵循上述“非互补”和“互补”原则，才能满足突变理论中分歧方程的要求.

在突变理论决策中对各控制变量间的相对重要性的考虑主要表现在相应的归一化公式中，主要控制变量在前，次要控制变量依次在后.为了避免控制变量的重要程度比较接近这个问题，根据专家经验和实践经验，舍弃次要且影响方案选择公正合理性的控制变量，同时淡化次要控制变量，突出起主导作用的控制变量，限制各控制变量评分的相对高低.

突变模型归一化公式中控制变量表征的是状态变量的不同方面的质态，其原始数据取值范围和度量单位互不相同，它们之间无法进行相互比较.因此，在使用归一化公式之前应依据突变理论决策的要求将底层指标的原始数据转化到［0，1］范围内的无量纲的越大越优型数值.

根据以上分析，可归纳出方案决策的具体步骤:

1)通过对典型海洋视景仿真系统分析，建立多层次多指标的综合评价指标体系.

2)利用式(1)-(11)对底层控制变量进行标准化，并计算各变量的初始模糊隶属函数值.

3)根据各子系底层控制变量数目选用相应突变模型的归一化公式，同时根据“非互补”或“互补”原则，利用式(12)-(13)不断递归运算，直至体系顶层，最终得到表征系统的总突变隶属函数值.

4)重复步骤1)-3)，分别计算出不同方案的突变隶属函数值.

5)根据不同方案总突变隶属函数值的排序，从而进行最终决策.

4 海洋视景仿真逼真度评定

海洋视景仿真作为一个复杂系统，在视景仿真系统设计中应当遵循一定的基本原则，已有原则主要体现在仿真实时性和一致性等特性，文中在此基础上提出和归纳海洋视景仿真所遵循的基本原则:

1)一致性.一致性是指在三维场景中各种画面在同一时空下的视觉效果，主要包括时空一致性和光照一致性.

2)实时性.视景仿真系统能够在限定的时间内进行实时仿真响应.

3)修正性.满足用户不需要修改内部代码的前提下自动或由用户手动修改其初始化参数.

4)组合性.根据用户需求，迅速地从模型库中提取所需分辨率仿真模型，并进行组合.

5)理解性.用户能够清晰地通过视觉理解视海洋战场仿真所表达的内容.

6)人机交互性.用户能够方便地在友好的人机界面上通过视点获取感兴趣的图形.

影响海洋视景逼真度的因素和环节很多，在考虑视景仿真遵循原则和处理控制变量的重要程度方法的基础上，文中针对典型海洋视仿真逼真度建立一套多层次多指标的逼真度评定指标体系［5-6］，比较全面地反映海洋视景仿真逼真度特性的全貌，各级指标及其描述见表2.

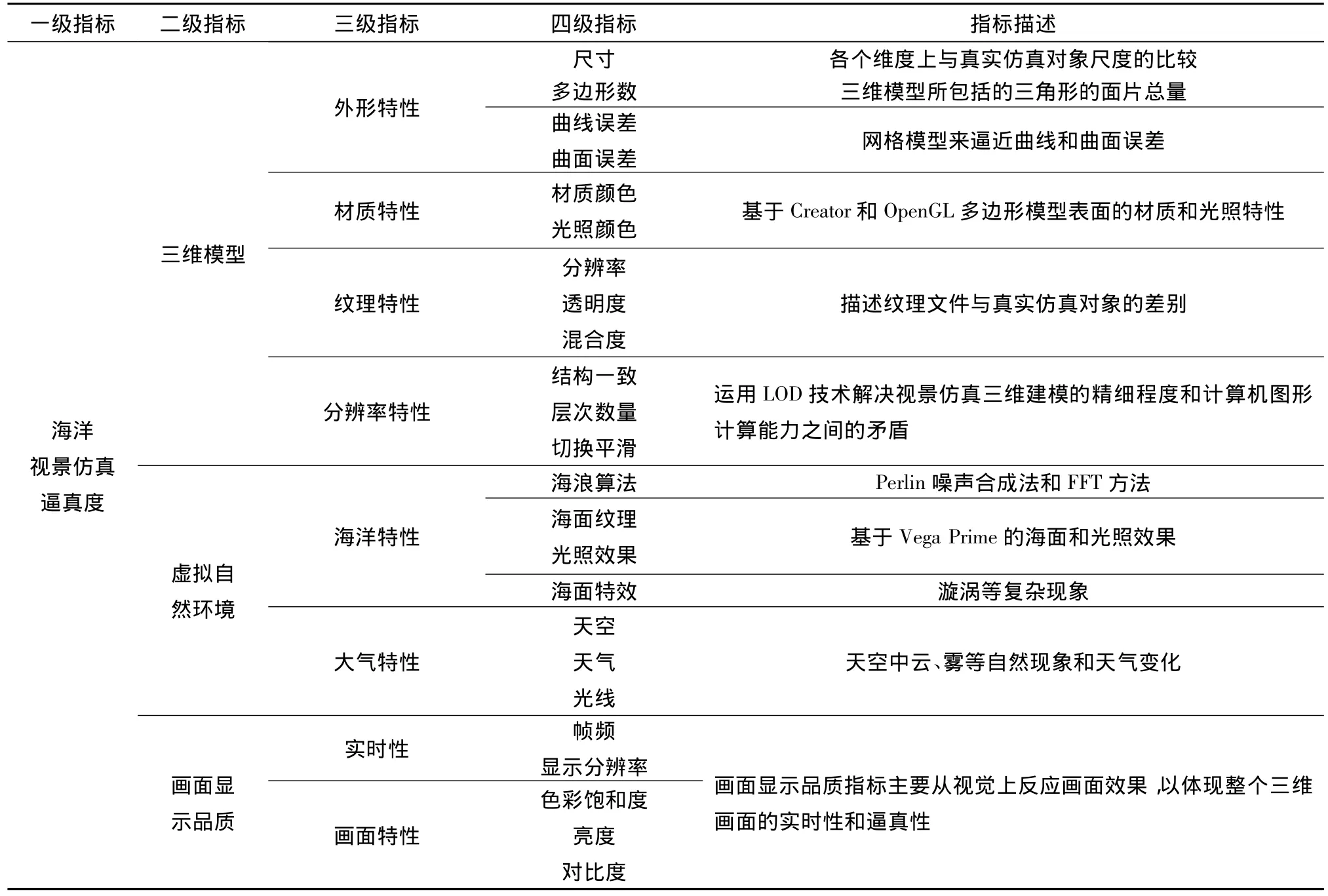
表2 视景仿真系统各级指标及其描述

3个海洋视景仿真画面分别如图2-4所示.其中三维实体主要用Creator和OpenGL进行建模，海浪采用Perlin噪声法和FFT方法的海浪模型，虚拟海洋自然环境采用Vega Prime.海洋视景仿真的测试环境:处理器为Intel(R)Core(TM)i7CPU/870，主频为2.93 GHz，内存为DRRII800/4 GB，显卡为NVIDA Ge-Force GTX 260/1 024 MB，硬盘为500 GB/7200 16M，软件配置为 Vega Prime 2.2，MultiGen Creator 3.0，OpenGL 2.0，Visual studio 2010，Window7.

根据方案决策模型对3个待选海洋视景仿真画面进行评定.

1)建立海洋视景仿真逼真度评定指标体系如表2所示.

2)根据专家对3个评价方案的底层指标进行梯形模糊评价，并计算初始模糊隶属函数值见表3.

图2 方案A

图3 方案B

图4 方案C

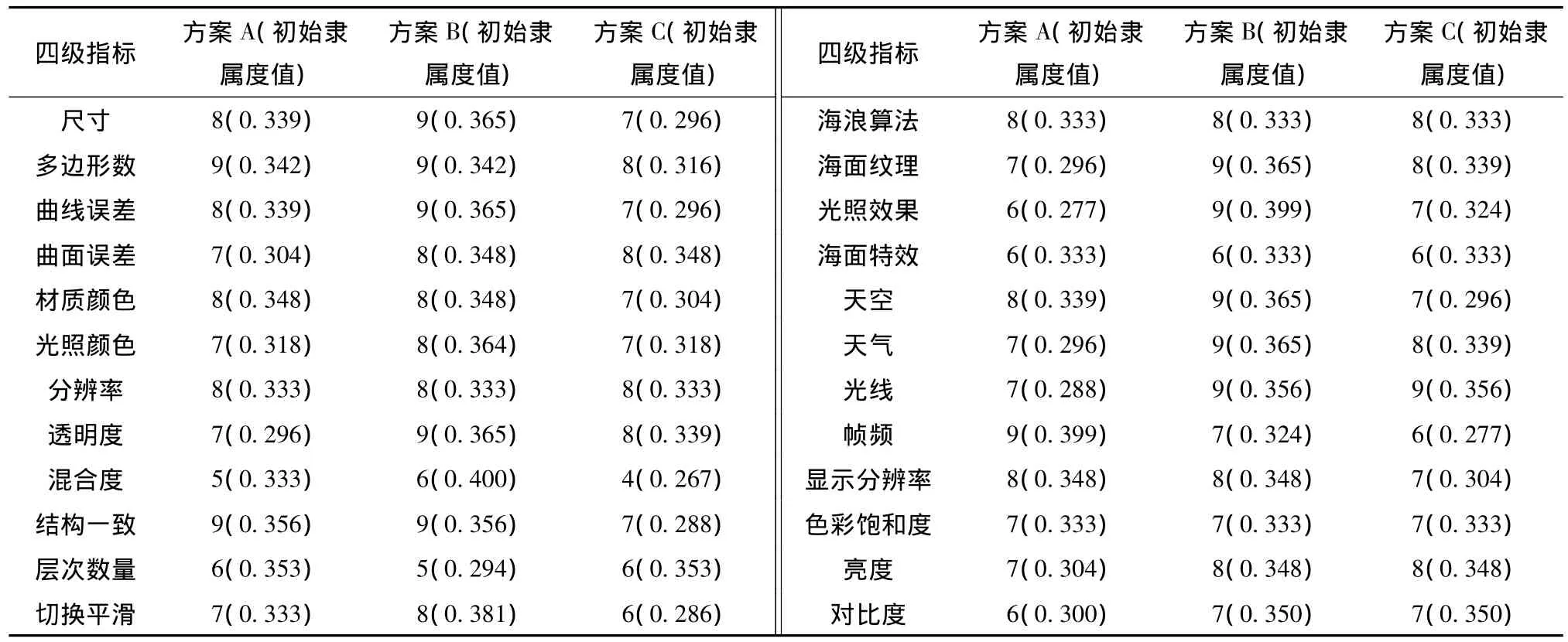
表3 四级指标量化及初始隶属度值

3)根据突变模型的控制变量及相应的归一化公式，可以分别计算出各个指标的突变数值，如三维模型中外形特性有4个指标应选用蝴蝶模型.三级指标中分辨率特性、大气特性和画面特性、二级指标画面显示品质，一级指标海洋视景仿真逼真度遵循“互补”原则，其他为“非互补”原则.

4)依次计算各级指标的突变隶属函数值和各方案的总突变隶属函数值.

5)根据各个方案总突变隶属函数值进行选优，最终结果如表4所示.

表4 决策评价最终数据结果

不同方案总突变隶属函数值如表4所示，可见B其为最佳方案.为了验证该方法的有效性，在相同条件下应用模糊层次分析法FAHP［5］进行验证.限于篇幅中间结果省略，最终计算结果见表4.根据表4可知，基于突变理论和梯形模糊数的决策方法能够有效解决逼真度评定问题.

5 结论

1)文中针对典型海洋视景仿真逼真度评定问题，总结出建立逼真的视景仿真系统所遵循的基本原则，建立了多层次逼真度的评定指标体系，提出了基于突变理论和模糊理论的决策方法，应用梯形模糊数方法可以对低层指标的不确定性进行有效的处理，利用突变理论方法利用归一化公式的内在机制动态递归决策.

2)该方法兼顾了专家知识的主观性和逼真度评定的模糊性，使决策或评判更趋于实际，为解决其他复杂多属性决策问题提供了一个新视角.

References)

［1］McMahan R P，Bowman D A，Zielinski D J，et al.E-valuating display fidelity and interaction fidelity in a virtual reality game［J］.IEEE Transactions on Visualization and Computer Graphics，2012，18(4):626-633.

［2］Behzadan A H，Kamat V R.Integrated information modeling and visual simulation of engineering operations u-sing dynamic augmented reality scene graphs［J］.Journal of Information Technology in Construction，2011，16:259-278.

［3］Ge Yong，Ge Zhenyang，Yi Huaifeng，et al.Visual simulation of upland rice root as related to soil compaction［C］∥Proceedings of2011Second International ConferenceonDigitalManufacturing＆Automation.Zhangjiajie:IEEE Computer Society，2011:1392-1394.

［4］Sampaio A Z，Viana L.Virtual reality used as a learning technology:visual simulation of the construction of a bridge deck［C］∥Proceedings of2013 8th Iberian Conference on Information Systems and Technologies.Lisbon:IEEE Computer Society，2013:1-5.

［5］唐 凯，康凤举.基于模糊AHP的视景仿真系统逼真度评估方法研究［J］.系统仿真学报，2008，20(22):6049-6053.Tang Kai，Kang Fengju.Evaluation method of visualization simulation fidelity based on fuzzy AHP［J］.Journal of System Simulation，2008，20(22):6049-6053.(in Chinese)

［6］王金华.基于仿真的自主水下航行器测试技术研究［D］.西安:西北工业大学航海学院，2009.

［7］Ohnishi S，Yamanoi T，Saito T.Fuzzy weights using sensitivity analysis for double inner dependence AHP［C］∥Proceedings of2012Annual Meeting of the North American Fuzzy Information Processing Society.Berkeley:IEEE Computer Society， 2012，doi:10.1109/NAFIPS.2012.6290990.

［8］张 晖，严新平，高 岩，等，基于模糊评价的安全感知与车速相关性分析［J］.江苏大学学报:自然科学版，2011，32(5):511-515.Zhang Hui，Yan Xinping，Gao Yan，et al.Relationship between driver safety cognition and vehicle speed based on fuzzy comprehensive evaluation［J］.Journal of Jiangsu University:Natural Science Edition，2011，32(5):511-515.(in Chinese)

［9］胡 文，刘红军.基于灰色理论的飞行模拟器逼真度评估［J］.先进制造与管理，2007，26(4):18-20.Hu Wen，Liu Hongjun.Flight simulator fidelity evaluation based on gray theory［J］.Advanced Manufacture and Management，2007，26(4):18-20.(in Chinese)［10］Yang Lei，Yang Xue，Dai Weidong.Performance evaluation of regional tourism cooperation based on triangular fuzzy number［C］∥Proceedings of2012International Conference on Management Science＆Engineering.Dallas:IEEE Computer Society，2012:867-873.

［11］李如忠，童 芳，周爱佳，等.基于梯形模糊数的地表灰尘重金属污染健康风险评价模型［J］.环境科学学报，2011，31(8):1790-1798.Li Ruzhong，Tong Fang，Zhou Aijia，et al.Fuzzy assessment model for the health risk of heavy metals in urban dusts based on trapezoidal fuzzy numbers［J］.Acta Scientiae Circumstantiae，2011，31(8):1790-1798.(in Chinese)