转柱泵瞬时流量的理论推导及数值模拟
2014-12-23孔繁余何玉洋
孔繁余,何玉洋,邵 飞,张 慧
(1.江苏大学流体机械工程技术研究中心,江苏镇江212013;2.北京航天航空大学能源与动力工程学院,北京100000)
国内外对于转柱泵瞬时流量的研究仍处于起步阶段.1982年 H.Fujiwara等[1]率先发明了转柱泵,介绍了转柱泵的工作原理和使用范围.聂如国等[2-4]开展过转柱泵的研发工作.至今为止,针对该泵的瞬时流量相关研究仍处于滞后阶段.在使用过程中,转柱泵的瞬时流量对泵的特性起着决定作用,所以对于瞬时流量的研究很有必要.笔者通过理论推导得到瞬时流量的理论计算公式,然后采用动网格技术和编译自定义函数,并结合k-ε湍流模型对内部流场进行非定常数值模拟[5].对比2种方法得到的结果,研究产生相异点的主要原因,分析几何参数以外的其他重要影响因素.
1 研究对象
转柱泵的主要几何参数:定子半径R=33.6 mm;转子外径r=31.5 mm;偏心距 ε =1.0 mm;转柱数为4;转柱外径rc=6.0 mm;转柱轴向长度B=8.0 mm;转柱槽宽度为 8.0 mm;转柱槽深度为 8.6 mm.转柱泵的结构如图1所示.

图1 转柱泵结构图
2 理论推导
转柱泵的排量是由相邻转柱围成的空间容积变化产生的[6].假设某相邻2转柱围成一容腔,如图2所示,右侧转柱表示2转柱旋转180°后所在的位置.且在左右两侧,转柱的位置关于x轴对称.3处抛面线1,3处是可变区域,剖面线2处近似为不变区域.因此转柱泵的排量与1,3处所占面积的变化有关.
在计算1处面积时,将转柱圆(半径为rc)近似为正方形,正方形的厚度t=2rc,1区域所占的面积就可以转化为如图3所示.其面积可以通过以下方法求出.如图3所示的坐标系Oxy,定子圆上某点的矢量半径为ρ(φ),是转角φ的函数,转角相对于x轴逆时针方向计算为正;V1为左侧容腔容积;V2为右侧容腔容积;容积缩小量为V=V1-V2.

图2 转柱泵截面面积图

图3 区域1面积图
滑片泵有许多滑片,每组相邻滑片围成的空间在转子旋转1周中经历1次吸排油过程,所以泵的排量为

平均理论流量为

式中:n为转速;z为转柱数.
由图3中的几何关系可得

式中:VF1,VF2分别为左、右侧容积内的滑片占用的容积.
ρ(φ)表示为[6]
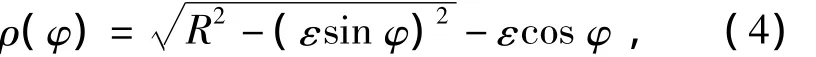
为了简化积分计算,将式(4)根号部分按照牛顿二项式定力展开级数,并忽略高次项可得

对于VF1,VF2有
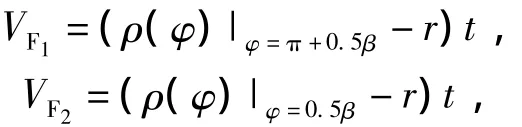
其中:

当滑片数z等于4时,有
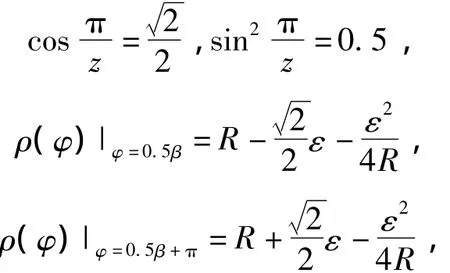
将上述各式代入式(3)得

所以,当滑片数z等于4时,单作用滑片泵排量和理论流量的计算公式为

因为是用正方形(t=2rc)的面积近似圆形(rc)的面积,所以对于求得的结果要添加修正系数:
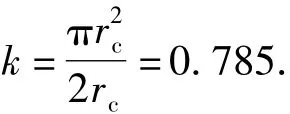
所以


瞬时流量可表示为抛面线3左右2处的面积S3,S'3分别为
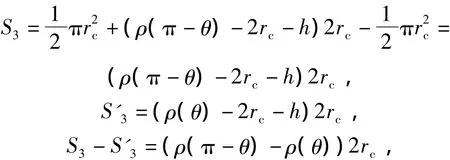
其中:

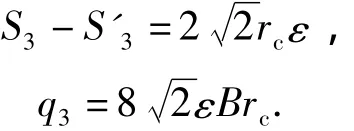
3区域的瞬时流量为
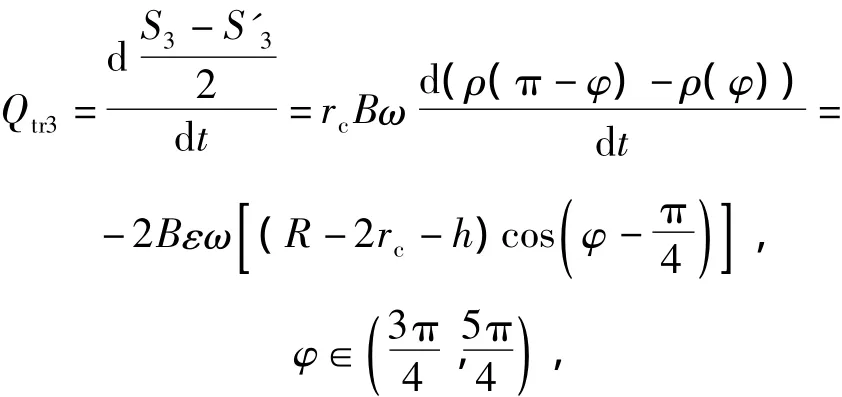
所以转柱数为4时的理论排量及理论流量为

推导出转柱泵瞬时流量的公式(8)后,代入各个参数,利用Matlab软件得到流量曲线,如图4所示.

图4 理论瞬时流量曲线
从式(8)及图4可以看出,转柱泵的瞬时流量成周期性脉动,脉动周期为,通过计算得到其平均流量为290.4 L·h-1,影响该泵瞬时流量的主要因素有偏心距ε,转柱数z,转柱的轴向宽度B,定子内壁半径R,转柱圆半径rc.
3 数值模拟
3.1 控制方程和边界条件
应用连续性方程和Reynolds平均Navier-stokes方程[7-8]模拟转柱泵内部流动,同时使用k-ε湍流模型封闭方程组,采用有限体积法将空间域上连续的控制方程转化为离散方程,压力和速度耦合方式选用PISO算法[8]进行非定常求解.设置进出口为压力边界条件,参考压力为1个大气压,固壁采用无滑移边界条件.输送介质为普通液压油,20℃时的体积弹性模量1.5 GPa,运动黏度为20×10-6m2·s-1.
3.2 动网格设置
使用In-Clinder模型定义旋转速度和时间步长,在实现动网格的过程中,未涉及网格分层和网格重新生成,网格节点位移是偏心距、旋转速度和转子半径的函数,在每一个时间历程内由用户自定义函数(UDF)[9]控制.
3.3 UDF运算
根据转柱槽内容积变化来编写UDF.转柱槽内容积旋转1周变化示意图如图5所示,大圆1和小圆2分别表示转柱槽上下表面质心运动轨迹.控制转柱槽内容积变化的UDF算法可以通过式(4)求得.
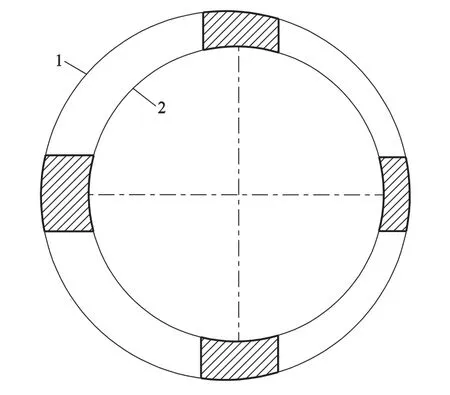
图5 转柱槽容积示意图
图6中,假设B点为上表面质心在二维图上的投影,连接原点O与B点,与下表面二维投影线相较于点A,又设圆Oj与OB交点为(xOj,yOj),交点满足下列关系:

式中:t0为旋转至某时刻所用的时间.
根据式(8)编写UDF程序.

图6 质心投影图
3.4 计算结果及分析
在排油窗口处设置监测点,监测该处的静压,得到转柱数为4,负载压力为0.25 MPa是瞬时流量随转子角度变化的模拟结果,如图7所示.
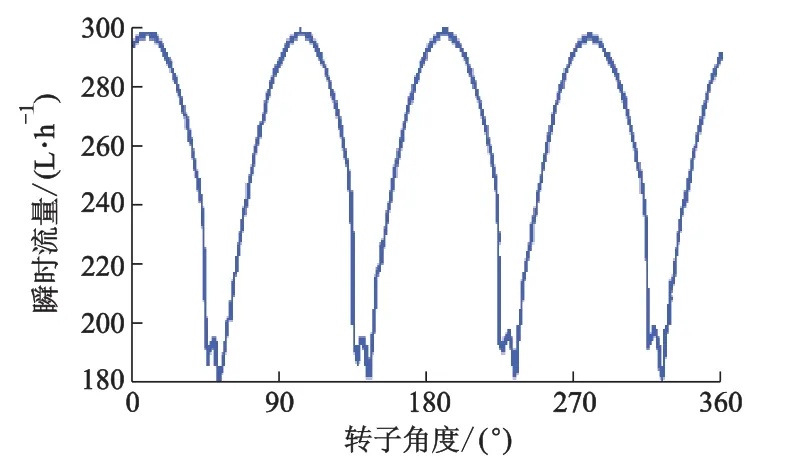
图7 模拟瞬时流量曲线
模拟出的平均流量为265 L·h-1,周期约为π/2;与理论推导的瞬时流量曲线相比,瞬时变化周期基本吻合,数值上偏低.这主要是因为理论值是按照几何体积变化计算得到的,但由于输送油具有可压缩性,体积的变化量一部分被输送油液的压缩量抵消了,导致实际出口流量略小于封闭容积的体积变化量.数值模拟设定了油液的体积弹性模量,计算的结果较为真实可信.
对比图7和图4明显的差别在于,图7中每个周期波谷会出现无规则振荡.主要是因为当转柱经过闭死区间,两转柱间的工作腔由于受到压缩[10-11],内部压力逐渐增大,当高压液体与排油窗口相连通时,高压工作腔突然卸压,瞬时流量迅速增大,配流盘内压力迅速升高并产生压力自由振荡,使瞬时流量出现上下波动,对工作腔产生很大的冲击.
转柱旋转角度 53.7°,54.6°和 55.6°的瞬时压力云图如图8所示,排油窗口处产生的一次压力波动,在这过程中配流盘转角是影响压力升高的重要因素,这样配流盘的转角也就直接影响了瞬时流量的上下波动,所以配流盘转角是除了转柱泵几何参数外的另一个重要影响因素.

图8 瞬时压力云图
4 结论
1)由理论推导和数值模拟方法,揭示了转柱泵的瞬时流量呈现周期性脉动,周期为
2)考虑了液压油的可压缩性,数值模拟结果比理论推导的结果略低,证明数值模拟更符合实际.
3)瞬时流量曲线与理论推导相比,配流盘内压力迅速升高,数值模拟的每个波谷会出现无规律的振荡.
4)配流盘内压力迅速升高造成了这种无规律的振荡,说明了配流盘转角对瞬时流量的脉动有着显著的影响,在设计过程中必须考虑到配流盘的转角.
References)
[1]Fujiwara H,Harada T,Murakami S,et al.Rotary roller vane pump made of specific-materials:USA,4362480[P].1982-12-07.
[2]聂如国.滚柱转子泵:中国,ZL9824459.5[P].1999-10-20.
[3]张生昌,方宏生,邓鸿英,等.电动喷雾器用高效低噪双作用滚柱转子泵研制[J].排灌机械,2008,26(4):18-21.Zhang Shengchang,Fang Hongsheng,Deng Hongying,et al.Design of double action roller rotary pump for electric sprayer with high efficiency and low noise[J].Drainage and Irrigation Machinery,2008,26(4):18-21.(in Chinese)
[4]张生昌,连加俤,邓鸿英,等.滚柱转子油泵滚柱与配流盘间隙的计算[J].排灌机械工程学报,2012,30(1):35-39.Zhang Shengchang,Lian Jiadi,Deng Hongying,et al.Calculation of gap between roller and valve plate for roller rotary oil pump[J].Journal of Drainage and Irrigation Machinery Engineering,2012,30(1):35-39.(in Chinese)
[5]王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004.
[6]何存兴.液压元件[M].北京:机械工业出版社,1982.
[7]邵 飞,孔繁余,王文廷,等.基于动网格的单作用滑片泵流量特性分析[J].流体机械,2011,39(8):14-18.Shao Fei,Kong Fanyu,Wang Wenting,et al.Analysis of flow characteristic in single-acting vane pump base on dynamic mesh method[J].Fluid Machinery,2011,39(8):14-18.(in Chinese)
[8]Riemslagh K,Vierendeels J,Dick E.An arbitrary Lagrangian-Eulerian finite-volume method for the simulation of rotary displacement pump flow[J].Applied Numberical Mathematics,2000,32:419-433.
[9]Issa R I.Solution of the implicitly discretised fluid flow equations by operator-splitting[J].Journal of Computational Physics,1986,62:40-65.
[10]Houzenaux G,Codina R.A finite method for the solution of rotary pumps[J].Computers&Fluids,2007,36(4):667-679.
[11]王 力,史振东,张建亭,等.变量叶片泵配流盘的设计理论[J].机械工程与自动化,2005(2):69-71.Wang Li,Shi Zhendong,Zhang Jianting,et al.Design of port plate of variable vane pump[J].Mechanical Engineering&Automation,2005(2):69-71.(in Chinese)
