基于Gabor特征与协同表示的人脸识别算法
2014-12-23张宏星李志勇
张宏星,邹 刚,赵 键,李志勇
(1.宁波工程学院 网络信息技术中心,浙江 宁波315211;2.国防科学技术大学 信息中心,湖南 长沙410073;3.中国人民解放军95380部队,广东 湛江524329)
0 引 言
稀疏表示 (sparse representation,SR)方法被广泛应用于模式分类与识别领域,Huang等人[1]将信号用一系列基函数进行稀疏编码,而后根据这些编码矢量来对信号进行分类。Wright等人[2]则提出了一种鲁棒的基于稀疏表示的人脸识别算法,该方法通过将待识别人脸图像用所有的模板图像进行稀疏编码表示后,再通过计算与各类模板图像集合之间的最小编码误差,来判断待识别人脸图像的类别归属。目前,这种基于稀疏表示的分类方法 (sparse representation based classification,SRC)已成功应用于人脸识别领域,并大大激发了基于稀疏的模式分类方法的研究工作。Gao等人[3]提出了基于核稀疏表示的人脸识别算法,Yang与Zhang[4]则利用基于Gabor特征的稀疏表示分类方法,通过自学习的Gabor不完备字典来降低算法的复杂度。Yang等人[5]将稀疏编码与线性空间金字塔匹配方法相结合,用于图像分类。文献 [6]综述总结了目前稀疏表示方法在计算机视觉和模式识别领域中的应用。
在基于稀疏表示的人脸识别方法中,一般假设待识别和模板库中的人脸图像均是已经校准后的图像,而目前稀疏表示方法也逐渐扩展至能处理未校准的或存在姿态变化的人脸图像,文献 [7]所提出的方法具备图像平面变换的不变性,文献 [8]所提出的方法则能适用于误配准和光照变化的情况,Peng等人[9]研究了如何同时将一系列线性相关图像进行校准。稀疏表示 (或称稀疏编码)的实质就是将一个信号y用字典来表示,即y ≈,其中α 为稀疏系数矢量。矢量α的稀疏性由l0范数来衡量,l0范数定义为矢量α 中的非零值的个数。由于l0范数最小化问题是NPhard问题,而l1范数最小化是最接近于l0范数最小化的凸函数,因此在稀疏表示方法中常利用l1范数来代替l0范数

其中,ε为误差阈值常量。尽管l1范数最小化要比l0范数最小化更简单有效,但是依然存在着计算复杂度较高,且目前出现了许多加速实现l1范数最小化求解的快速算法。根据文献 [10]的综述总结,目前有5种代表性的快速l1范数最小化求解方法:梯度投影法、同伦分析方法、迭代收缩阈值法、最近邻梯度法以及扩展拉格朗日乘子法。对于存在噪声的数据,一阶l1范数最小化求解方法 (典型算法如SpaRSA[11],FISTA[12]和ALM[13]等)更为有效。而对于人脸识别,同伦分析方法[14]和l1-ls 方法[15]则更加精确并具有更快的计算速度。
尽管基于稀疏表示的分类方法 (SRC)[2]成功应用于人脸识别领域并取得了不错的效果,但是其工作机制原理却仍然存在着诸多疑问。大多数文献均是着重强调了在人脸分类中l1范数稀疏特性的重要性,而协同表示 (collaborative representation,CR)[16]的重要性 却被忽视了。协同表示的质就是利用所有类别中的训练样本来共同表示待识别样本y。l1范数最小化问题使得基于稀疏的分类方法 (如SRC方法)的计算复杂度较高,而SRC 方法能成功应用于人脸识别是否就是l1范数的稀疏特性所决定的问题,一直存在 着诸 多疑问[16-18]。
针对上述疑问,Zhang等人[16]分析了SRC 方法的基本原理,在解释了稀疏性能够有效增强分类区别能力的基础之上,提出了在基于稀疏表示的分类方法中,协同表示要比l1范数的稀疏特性更为重要。由此,文献 [16]提出了一种基于协同表示和规则最小二乘的分类方法 (CRCRLS),与SRC方法相比,CRC-RLS具有较好的分类效果,并较大程度降低了计算复杂度。但是,由于CRC-RLS方法直接采用人脸图像的灰度特征,当存在光照、姿态等变化时,识别效果下降较快。本文提出了一种新的基于Gabor特征和协同表示的人脸识别算法,在提取人脸图像的Gabor特征后,再结合协同表示的方法进行人脸识别,取得了较好的识别效果。
1 Gabor特征提取
Gabor滤波器最早由David Gabor在1946 年提出,后来研究发现可以用Gabor滤波器来模拟人类视觉细胞感受野。Gabor滤波器能有效地提取图像多尺度下的局部方向性特征,其已成功应用于人脸识别领域[19]。Gabor特征属于局部区域特征,因此在光照、表情以及姿态等的变化下,Gabor特征要比其它全局特征如特征脸 (Eigenface)、随机脸 (Randomface)等更具鲁棒性和不变性。
Gabor滤波器[21]定义见式 (1)
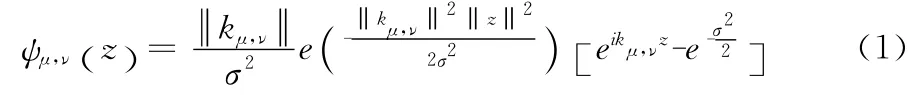
其中,μ 和ν 分 别 表 示Gabor 核 的 方 向 和 尺 度,z =(x ,y) 为图像的像素坐标值,小波矢量kμ,ν定义见式 (2)

图像中提取Gabor特征就是利用式(1)所示的Gabor滤波器组与图像进行卷积后完成的。令I x,( )y 为图像的灰度值分布,而图像I与一个Gabor核的卷积定义见式(3)
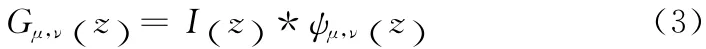
其中,z= (x ,y) ,“*”为卷积算子,Gμ,ν(z) 则代表了方向μ 与尺度v 下的Gabor核与图像的卷积结果。本文中采用的是5个尺度和8个方向下的Gabor滤波器组,因此最终所提取的图像 I (z) 的Gabor特征为集合
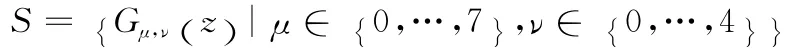
根据卷积定理可知,可通过快速傅里叶变换 (FFT)来求解式 (3)中的Gμ,ν(z)

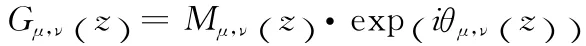
式中:Mμ,ν()z ——幅度值,θμ,ν()z ——相位值。幅度值信息Mμ,ν()z 包含了图像中的局部能量的差异性。图1显示了Gabor核在5 个尺度,8 个方向上的幅度值图像,可见Gabor特征具有尺度性、局部性以及方向性的特点。

图1 各参数为σ=2π,kmax =,f =时的Gabor核
为了能充分体现出Gabor小波的空间尺度性、空间局部性以及方向可选择性,本文将所有尺度和方向下的卷积结果串联起来形成了扩展的Gabor特征矢量χ,在串联之前,首先将每一个Gμ,ν(z)按照比率ρ进行下采样以降低矢量维数,再将其归一化为零均值和单位方差的矢量,最后将Gμ,ν()z 按行 (或列)的方向串联得到了扩展的Gabor特征矢量χ(ρ)
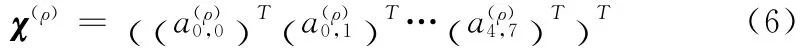
2 基于Gabor特征与协同表示的人脸分类识别算法(Gabor-CRC)
本节首先简要介绍了经典的基于稀疏表示的人脸分类识别算法 (SRC),在分析了SRC的优缺点后,提出了本文新的基于Gabor特征与协同表示的人脸分类识别算法 (Gabor-CRC)。
2.1 基于稀疏表示的人脸分类识别算法 (SRC)
令Xi= [si,1,si,2,…,si,niRm×ni 为第i类人脸的训练样本集,其中si,j,j=1,2,…,ni为第i类人脸的第j 个样本的m 维特征矢量。假设总共有K 类训练样本,则令所有的训练样本集为:X = [X1,X2,…,XK]。假设一个测试样本图像为y∈Rm,则可以将其用训练样本集来线性表示为y ≈ Xα, α = [α1;…αi;…αK], 其 中 αi=[αi,1,αi,2,…,αi,ni]T∈Rni 为与第i类的编码系数矢量。如果测试样本y属于第i类人脸,则通常会有yi≈Xiαi成立,这也意味着系数矢量α中的大多数k≠i时的系数αk几乎均为零,而仅有αi具有非零值
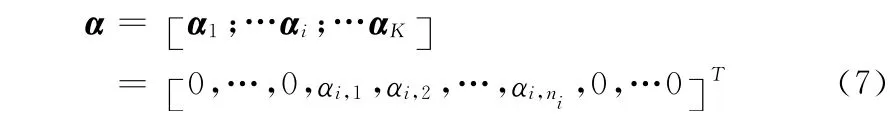
因此,由矢量α中的稀疏的非零值可以得到测试样本y的类属信息。具体的SRC算法流程见表1。

表1 SRC算法流程
2.2 基于协同表示的人脸识别算法 (CRC-RLS)
从表1所示的SRC算法流程中可知,SRC 算法有两个关键之处:第一,测试样本y 的编码稀疏矢量必须是稀疏的;第二,测试样本y 的稀疏编码是协同作用于全部训练样本集X 上的,而不仅仅是作用于每类训练样本的子集Xi。假设y属于数据集中的某一类,则y 基于X 的线性表示的系数是最稀疏的,因此具备可区分性从而能得到y 的类属信息。
在人脸识别中,每一类人脸图像均位于Rm中的子空间,即m 维的人脸图像可以用更低维的特征矢量来表示。如果采用第i类训练样本集合Xi来作为该类的字典,则Xi中的原子 (训练样本)将是相关的。假设每类训练样本是足够多,则所有属于第i类的图像完全能由Xi来表示,因此Xi是一个超完备字典。而由于第i类的训练样本间的相关性可知,属于第i类的测试样本y 能用字典Xi稀疏地表示。由上分析可知,为了使得降维后字典Xi满足超完备的要求,SRC算法要求训练样本足够多,但是人脸识别却属于典型的小样本问题,一般情况下Xi是非完备的。如果利用Xi来表示y,即使当y属于第i类也会导致较大的表示误差,因此最终导致分类结果的不稳定。最直接的解决方法是利用第i类的更多样本来表示y,但实际应用中却难以实现。
针对人脸识别应用而言,不同类别的人脸图像往往具有一定的相似性。也就是说,第j类的人脸样本有助于表示第i类的测试样本。在SRC 算法中,通过将所有其它类别训练样本来作为每类中可能的训练样本可以解决 “样本的缺失问题”,也就是在基于l1范数的稀疏性约束条件下,将测试样本y用所有训练样本X = [X1,X2,…,XK]来协同表示。文献[16]在分析了SRC算法的基本原理后,提出了SRC算法对于分类的有效性不是取决于基于l1范数的稀疏性,而是由其内在的协同表示性所决定的,因此可将基于l1范数的稀疏性约束条件简化为最小二乘约束问题,从而提出了基于协同表示的人脸分类识别算法(CRC-RLS)。
2.3 本文算法 (Gabor-CRC)
文献 [16]所提出的基于协同表示的人脸分类识别算法仅仅利用了原始人脸图像的特征 (灰度分布),当存在光照、表情以及姿态等变化时,存在识别准确率下降较快的问题,为进一步提高算法的准确率以及鲁棒性,本文将扩展的Gabor特征与CRC算法相结合,提出了一种新的基于Gabor特征和协同表示的人脸分类识别算法。
根据前面第二节中所提出的扩展的Gabor特征定义,提取所有训练样本集图像的扩展Gabor特征,设第i类训练样本集合所提取的对应扩展Gabor特征集为Xi=[χi,1,χi,2,…,χi,ni],则所有类的训练 样本Gabor特征集 为X =[X1,X2,…,XK]。为了能以较少的计算代价,用所有训练样本特征集来协同表示测试样本,可以将SRC 算法中的基于l1范数的稀疏性约束条件简化为规则化的最小二乘方法,即将式 (8)简化为

与SRC算法相比,CRC方法求解式 (11)所示的规则化最小二乘问题要远比求解式 (8)所示的基于l1范数的最优化问题更为简单。可以通过解析方法求得基于协同表示方法的最优解

令投影矩阵P= (XTX +λI)-1XT,则易见P是独立于y的,因此其可以在训练阶段就事先计算得到。如果一个测试样本y需要进行分类识别,可以通过将y 投影至P 上从而得到Py,由此可知CRC方法要比SRC 方法具有明显的速度优势。表2为本文的基于Gabor特征与协同表示的人脸分类识别算法流程。
3 实验结果与分析
本节分别在3 个标准人脸识别数据库,即Extended Yale B数据库、AR 数据库以及ORL 库中进行了本文所提的Gabor-CRC算法性能对比实验,本文选取了如最近邻分类算法 (NN)[2]、基于支持矢量机的分类算法 (SVM)[2]以及SRC[2]和CRC-RLS[16]等经典算法来作为比较算法。

表2 Gabor-CRC算法流程
3.1 Extended Yale B数据库上的实验
Extended Yale B数据库包含了38个人的2414幅正面人脸图像,考虑到经典的CRC以及SRC算法中均采用的是特征脸特征,因此,为了减少特征提取的复杂度,本实验中将该库中的人脸图像剪切和归一化为54×48像素大小的图像,这些图像均在不同的光照环境中所拍摄而成的。随机将数据库中的各类人脸对等分为两半,即每个人的人脸图像中有32张作为训练样本,而其余的作为测试样本。表3显示了NN算法、SVM 算法、SRC 算法、CRC-RLS算法与本文的Gabor-CRC算法的识别率与特征维数之间的关系。

表3 不同算法在Extended Yale B数据库上的识别性能比较
3.2 AR 数据库上的实验
在AR 数据库中选取具有光照变化以及表情变化的人脸图像作为实验数据,其中包括了50个男性和50个女性的正面人脸图像,本文实验中依然随机选取每个人的7幅人脸图像作为训练样本,而另外的7幅作为测试样本,所有的人脸图像均规则化为60×43像素大小的图像。实验的比较结果见表4。可以看出本文算法在维数较高时要比其它经典算法的识别率高很多,这也充分说明了基于Gabor特征和协同表示的人脸识别算法对光照和表情变化具有较好的鲁棒性。
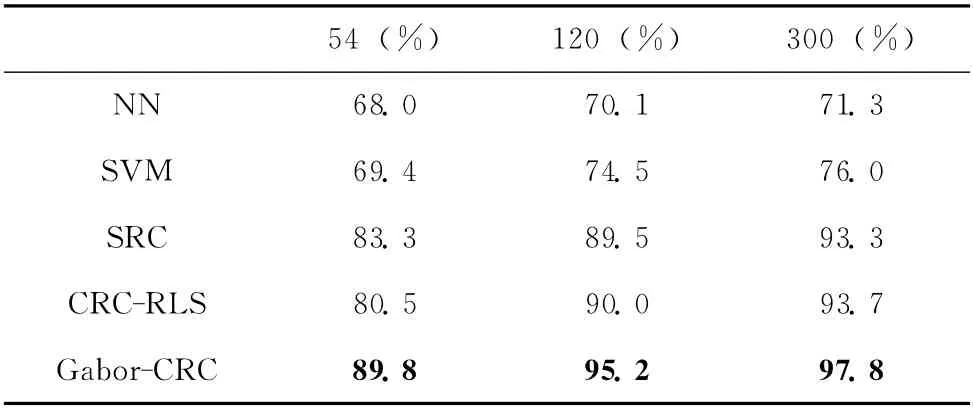
表4 不同算法在AR 数据库上的识别性能比较
3.3 ORL数据库上的实验
ORL数据库中包括了40 个人的人脸图像,其中每个人均有10 幅人脸图像,每幅图像均具有不同的姿态、表情,因此,在ORL数据库上的对比实验将验证本文算法对人脸的姿态、表情变化的鲁棒性。同样,对于每类人脸均随机抽取一半的人脸图像作为训练样本,而另外一半作为测试样本进行对比实验,最终结果见表5。可以看出,本文算法在ORL库上的识别率远高于其它基于特征脸的经典人脸识别算法。
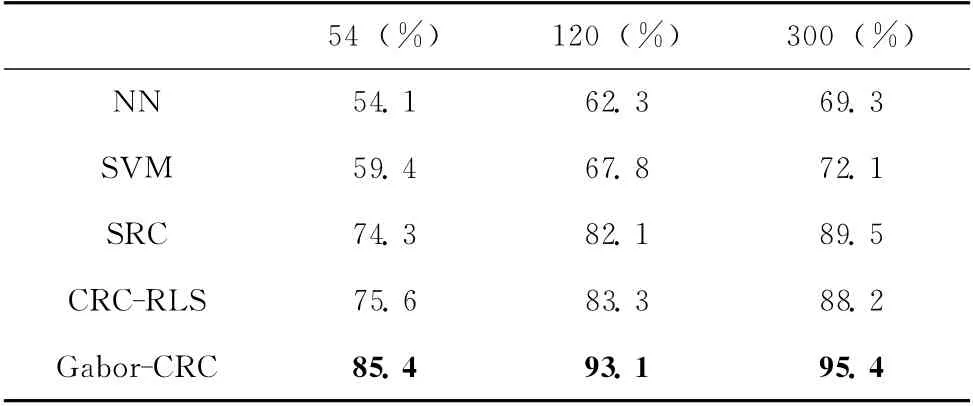
表5 不同算法在ORL数据库上的识别性能比较
3.4 算法速度的比较
本节将比较利用不同的快速l1范数最小化方法的SRC算法、CRC-RLS算法与本文的Gabor-CRC算法之间的算法速度,其中,SRC算法所采用的快速l1范数最小化方法包括Homotopy方法[14]、l1-ls 方 法[15]和ALM[13]。将 各 算 法所提取的特征维数固定为300后,分别比较各自的平均运行时间,结果见表6,可以看出,本文算法要比SRC 算法快很多,由于需要提取Gabor特征,因此要比CRC-RLS算法稍慢。
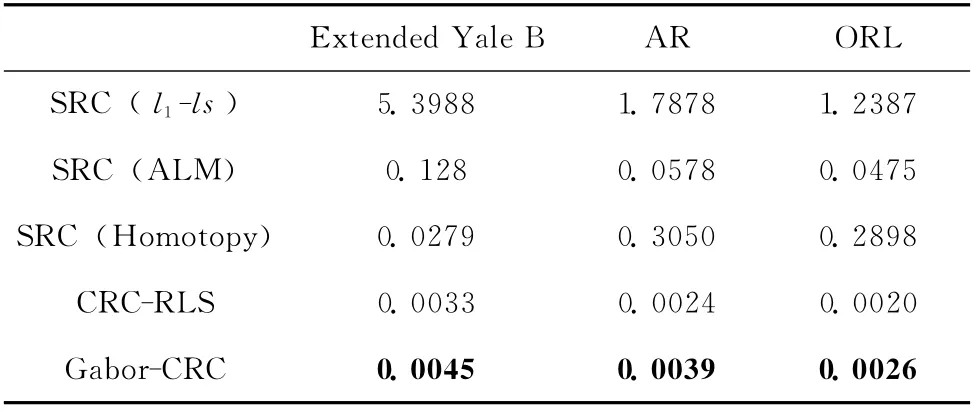
表6 不同算法在各数据库上的算法速度比较 (单位:秒)
4 结束语
基于稀疏表示的分类识别算法 (SRC)需要求解基于l1范数最小化问题,使得该方法计算复杂度较高。基于协同表示和规则最小二乘的分类识别方法 (CRC-RLS)指出协同表示特性决定了SRC算法的分类有效性,从而提出将基于l1范数最小化问题简化为最小二乘约束问题,从而使得算法复杂度得到大幅降低。本文首先提取人脸图像的规则化扩展Gabor特征,然后,将Gabor特征与协同表示的方法有机结合,最终提出了一种新的基于Gabor特征与协同表示的人脸识别算法 (Gabor-CRC)。经过在标准数据库上的统计实验,实验结果表明,本文所提的新方法不仅对于光照、表情和姿态等变化具备较强鲁棒性,而且运行速度较快。
[1]Huang K,Aviyente S.Sparse representation for signal classification [C]//Advances in Neural Information Processing Systems 19,2006.
[2]Wright J,Yang A Y,A Ganesh,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31 (2):210-227.
[3]Gao Shenghua,Tsang I W,Chia L.Kernel sparse representation for image classification and face recognition[C]//Proc of the 11th European Conference on Computer Vision,2010:1-14.
[4]Yang M,Zhang L.Gabor feature based sparse representation for face recognition with Gabor occlusion dictionary [C]//11th European Conference on Computer Vision,2010.
[5]Yang J,Yu K,Gong Y,et al.Linear spatial pyramid matching using sparse coding for image classification [C]//IEEE Conference on Computer Vision and Pattern Recognition,2009:1794-1801.
[6]Wright J,Ma Y,Mairal J,et al.Sparse representation for computer vision and pattern recognition [C]//Special Issue on Applications of Compressive Sensing &Sparse Representation,2010:1031-1044.
[7]Huang J Z,Huang X L,Metaxas D.Simultaneous image transformation and sparse representation recovery [C]//IEEE Conference on Computer Vision and Pattern Recognition,2008.
[8]Wagner A,Wright J,Ganesh A,et al.Towards a practical face recognition system:Robust registration and illumination by sparse representation [C]//IEEE Conference on Computer Vision and Pattern Recognition,2009.
[9]Peng Y,Ganesh A,Wright J,et al.RASL:Robust alignment by sparse and low-rank decomposition for linearly correlated images [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34 (11):2233-2246.
[10]Yang A Y,Ganesh A,Zhou Z H,et al.Fast l1-minimization algorithms and application in robust face recognition [J].IEEE Transactions on Image Processing,2013,22 (8):1057-7149.
[11]Wright S J,Nowak R D,Figueiredo M A T.Sparse reconstruction by separable approximation [C]//ICASSP,2008.
[12]Beck A,Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems [J].SIAM Journal on Imaging Science,2009,2 (1):183-202.
[13]Yang J,Zhang Y.Alternating direction algorithms for l1-problems in compressive sensing [C]//CAAM,2009.
[14]Malioutove D,Cetin M,Willsky A.Homotopy continuation for sparse signal representation [C]//ICASSP,2005.
[15]Kim S J,Koh K,Lustig M,et al.A interior-point method for large-scale l1-regularized least squares[J].IEEE Journal on Selected Topics in Signal Processing,2007,1 (4):606-617.
[16]Zhang L,Yang M,Feng X C.Sparse representation or collaborative representation:Which helps face recognition [J].ICCV,2011.
[17]Rigamonti R,Brown M,Lepetit V.Are sparse representations really relevant for image classification [C]//CVPR,2011.
[18]Shi Q,Eriksson A,Hengel A,et al.Is face recognition really a compressive sensing problem [C]//CVPR,2011.
[19]Kundra H,Arshima E R,Verma M.Image enhancement based on fuzzy logic[J].Computer Science and Network Security,2009,10 (9):141-145.
