基于显式算法的改进型SHTB实验模型研究

张君发，鞠玉涛，王蓬勃，许进升

（1.南京理工大学 机械工程学院，江苏 南京210094；2.上海航天动力技术研究所，上海201109）

0 引 言

霍普金森实验装置是研究材料动态力学性能最有效的实验装置之一。1949年Kolsky提出用于测试材料动态压缩力学性能的分离式霍普金森压杆实验技术的半个多世纪以来，该实验技术被应用于多种材料在高应变率下力学性能的测量中［1］。随着霍普金森杆实验技术的发展以及材料测试的要求，对霍普金森实验设备和实验精度的要求日益提高，许多学者通过计算机仿真或者实验的手段对该技术进行了更深入的研究，Ramírez［2］利用有限元方法研究波在杆中的传播并分析了整形片的作用；臧小为［3］对霍普金森杆过载波形整形以及系统分析软件进行了相关研究；丰平［4］研究了霍普金森杆中试件变形过程中应力均匀性和恒应变率的实现问题；焦楚杰［5］采用显示动力有限元软件LS－DYNA 对钢纤维高强混凝土的霍普金森压杆冲击实验过程进行了数值仿真。利用霍普金森压杆测试一般材料的动态压缩特性已趋于成熟。

霍普金森拉杆 （SHTB）装置是在霍普金森实验技术的基本原理上改进的用于测量材料动态拉伸力学性能的装置。典型的Hopkinson拉伸装置有块－杆型和间接式杆－杆型，包括摆锤式和旋转圆盘式。但是无论采用摆锤还是旋转圆盘都因其结构复杂、加工精度高、造价高不利于推广。2000年Nemat－Nasser研制出带有吸收杆，能实现单次加载的直接拉伸式杆—杆型霍普金森拉杆装置。它与压杆不同之处主要在于这种装置是用一沿入射杆运动的管状子弹打击入射杆端的法兰盘直接在入射杆中形成拉伸波，以后的传播特性与压杆中的压缩波完全类似。

然而在实际实验中由于装置本身的复杂性以及实验材料的多样性，尤其是在软质复合材料的高应变率拉伸研究中，传统的SHTB 装置不能满足实验要求。SHTB 实验技术同样也是建立在两个基本假定基础上的，即：杆中一维应力波假定；试件应力／应变沿其长度均匀分布假定［6］。针对SHTB的基本假定以及复杂材料动态拉伸实验的要求，传统SHTB装置在实验中具有以下不足：①直接拉伸式杆－杆型霍普金森拉杆装置原理的提出假设杆端部的法兰与入射杆是一体构造，这虽然满足一维应力波假设，但增加了其加工制造过程中的困难；②现今SHTB 装置的杆径一般不超过20mm，因为随着杆径的增加，波的弥散效应更加明显［7］，可能无法满足应力波的一维假定，然而复合材料的动态研究中需要保证试件的尺寸足够大以满足均质假设，因此需要更大尺寸的SHTB装置；③动态拉伸加载方式使得试件的安装和固定十分困难，传统SHTB 装置上无法获得软质复合材料的有效数据。

本文在传统SHTB装置的基础上，对模型的结构进行改进：将入射杆撞击端的法兰盘与入射杆之间采用螺纹连接，由于螺纹的增加使得应力波的传播变得更加复杂；将SHTB仿真模型的杆径扩大为30mm；对拉伸试件的装夹方式进行改进。基于ABAQUS显式算法数值仿真技术研究改进型霍普金森拉杆中入射波、反射波和透射波的一维假设以及试件的应力均匀进行研究，验证数据的有效性。利用数值仿真技术对实验装置模型的分析为SHTB装置的改进设计和实验提供理论基础。

1 物理模型及参数

图1为30mm 直接拉伸式杆－杆型SHTB装置的结构示意图，管状子弹在压差的作用下加速获得一定的速度撞击入射杆上的法兰，在入射杆中产生拉伸波。SHTB 杆和管状子弹材料选为LC4铝，密度ρ＝2850kg／m3，弹性模量E＝74GPa，泊松比ν＝0.33，杆直径为30mm，入射杆、透射杆和吸收杆的长度分别为3000mm、2000mm 和1000mm，管状子弹的内径为35mm，管状子弹外径和法兰盘直径为46mm，子弹长度为300mm。法兰盘与入射杆一端、入射杆的另一端与试件以及透射杆与试件之间都采用螺纹连接，螺纹大小为M16。

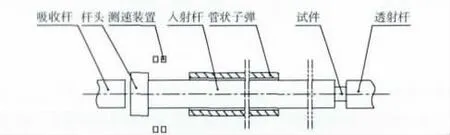
图1 30mm 霍普金森拉杆结构

该模型的加载方式是管状子弹以一定的速度撞击入射杆一段的法兰盘，所以数值模拟中赋予管状子弹18 m／s的初始速度。由于模型中的部件全部满足轴对称，为了在一定的计算资源中模型能够划分更小的单元，全部采用二维轴对称计算模型。

图2 （a）为法兰－杆一体的拉伸入射杆，为了便于拉伸杆件的加工，将入射杆撞击端的法兰盘与入射杆之间采用螺纹连接，如图2 （b）所示。

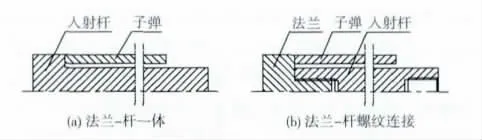
图2 入射杆撞击端结构

SHTB实验研究过程中，试件的安装和固定一直是研究的难点，尤其是对于软质材料的拉伸始终没有得到有效解决。Wang［8］利用巴西圆盘的SHPB装置对材料的拉伸性能进行研究，然而这种利用压杆研究拉伸性能的方式具有一定的局限性并且不适合软材料。Nicholas利用SHPB 对入射杆加载压缩波，当波传到试件处，试件外的刚性管将波传递到透射杆，压缩波在透射杆自由端反射为拉伸波对试件进行加载，拉伸试件采用螺纹与两杆连接。Fu［9］将两端带螺纹的试件直接装夹在直接拉伸式杆－杆SHTB 装置上。杆件和试件之间的螺纹连接使得试件处的应力波传播十分复杂，试件中的螺纹间隙容易造成应力集中，影响实验结果的可信度；每个试件两端都加工成带螺纹的哑铃型使得实验周期大大增加，尤其是软材料的螺纹加工难度大、固定效果不好。Sun［10］将哑铃型试件直接粘贴在入射杆和透射杆件之间，采用直接拉伸式杆－杆型SHTB 加载拉伸波。这种方式使得实验周期很大，每次实验都需要单独粘接固化，哑铃型试件粘接使得试件标距不容易确定，且试件长度较大无法实现应力均匀。

本文针对复合材料SHTB 拉伸试件的特点，改进了试件的装夹方式，如图3所示。采用两个带有螺纹的试件接头将试件与两杆件相连，试件两端粘接在接头的端部。这样使得拉伸试件的长度可以足够短，更容易满足应力均匀假设，同时试件接头的设计使得实验前可将多个试件与多组试件接头粘接固化，缩短实验周期。拉伸试件的尺寸为Φ16×5mm。

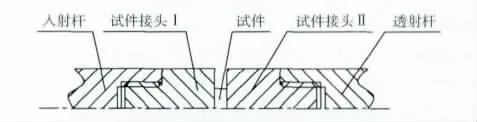
图3 SHTB拉伸试件连接

2 数值仿真过程及结果

2.1 入射波的一维验证

SHTB装置中由子弹撞击杆端法兰，然后间接对杆产生一个拉伸波。本文提出的实验台模型是在法兰与杆之间采用螺纹连接的方式，如图2所示。为了验证该模型中螺纹连接的影响，将其与尺寸相同的法兰－杆一体的模型进行对比，同时螺纹连接分别采用M16×1、M16×1.5和M16×3这3种不用的螺纹大小进行数值模拟。由于螺纹连接处的受力情况很复杂，所以螺纹连接处的网格加密。

分别对两种模型的子弹加载相同的初速度，图4和图5分别为模型应力等值线图和入射杆中点表面处的应力波形图，其中图4中240us为入射杆中点附近的应力等值线图，图4 （b）中螺纹代号为M16×1.5。从仿真结果可以看出：无论是法兰－杆一体模型还是法兰－杆螺纹连接模型，在其初始法兰位置处产生的应力等值线很乱，杆中的应力波不稳定；由于应力波传播过程受扰动介质与其周围介质的不断产生相互作用力，细长杆上应力等值线会逐渐变得垂直于杆轴方向，应力波逐渐变得稳定，当应力波传到干中点附近处其等值线变成一系列跟杆轴相垂直的平行线，杆中的应力波实现了稳定传播；螺纹对入射杆中点表面的波形基本没有消极影响，反而具有一定的滤波作用，减小加载波在杆件中点处的振荡。

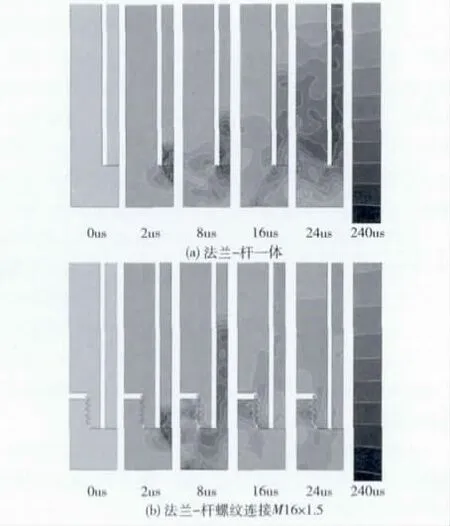
图4 入射杆中波形的产生及传播

从应力等值线图中可以看出应力传播过程是由混乱逐渐发展为较理想的一维应力波的，为更细致地了解这发展过程，在距离入射杆撞击端距离为1R、5R、20R 和50R 这

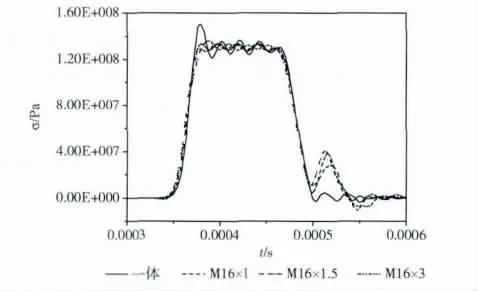
图5 入射杆中点表面处的应力波形图

4个截面处分别选取杆中心、距杆中心0.5R 处以及杆外表面3个不同单元，查看其应力情况，结果如图6所示。

图6 入射杆应力波形图

从图6中可以看出，法兰－杆一体模型在距离杆头1R的距离上已经基本实现一维传播，但波形振荡剧烈，随着波在入射杆中的传播振荡逐渐减小，并且满足σ0R＝σ0.5R＝σ1R，实现一维传播；法兰－杆螺纹连接模型在靠近头部处沿径向应力分布不均匀，并且波形有很强烈的震荡，随着波在杆中的传播其应力也能够逐渐趋于均匀，当距离L 达到20R 和50R 处，波形振荡减小，同一截面处的应力基本相等，杆件的弥散效应不明显。

综合以上仿真结果可知：改进后的法兰－入射杆螺纹连接模型对加载波有高频过滤效应，入射波满足一维应力波假设。

2.2 反射波的验证

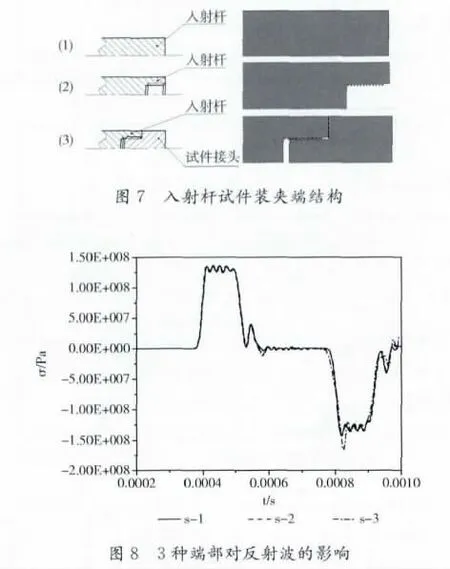
为了验证本文提出的试件装夹方式的有效性，首先需要研究入射杆试件接头的螺纹连接对反射波的影响。图7所示为入射杆试件装夹端的结构示意图。

图8为图7中3种形式对反射波的影响，从图8中可以看出：试件接头与入射杆连接处螺纹连接并没有使波形产生强烈振荡，加载波在入射杆端能够完全反射进入入射杆，所以该模型满足SHTB杆反射波的要求。

2.3 透射波的验证

根据应力波原理可知SHTB杆中试件的应力为

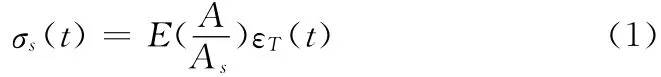
式中：A 和As分别是杆和试件的横截面积；E 是弹性杆的模量；εT（t）是透射波的应变值。从式中可以看出试件中的应力与透射波信号相关，为了验证该装置能理想地透射加载信号，数值仿真中采用两端带有螺纹的试件接头与入射杆和透射杆相连，试件接头的材料与杆材料相同。为了验证拉伸波的透射状况，两个试件接头中间不放置试件，假设其粘结在一起。

给管状子弹以某一初始速度，利用数值模拟仿真获得入射波、透射波以及试件接头内波形的对比如图9 所示。图9中将透射波和试件接头内应力波平移到与入射波相同的时间点，可以看出透射波和试件接头内的加载波的幅值和波宽都跟入射波相同，拉伸波可以无影响地透射到透射杆中，说明这种结构对透射波的传播没有消极影响，满足实验要求。

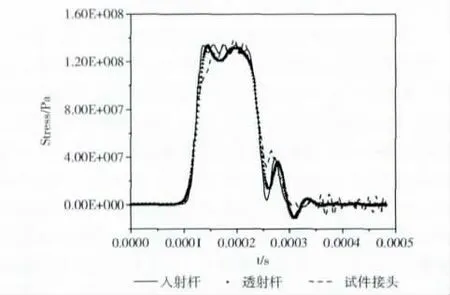
图9 波形传播对比

2.4 试件应力均匀性验证

依据Hopkinson杆的实验原理，实验过程中要求试件中应力均匀，即有εi（t）＋εr（t）＝εt（t），获得的入射波和反射波之和应该与获得的透射波相等。为了验证图3中模型满足应力均匀假设，在仿真过程中试件的材料需设为粘弹性材料，具体数值利用孟红磊［11］在低应变率下获得的改双基推进剂材料的拉伸力学性能。由于该模型在实际实验过程中采用强力胶粘贴在试件夹头上，所以数值仿真中试件两端与试件接头Ⅰ和试件接头Ⅱ之间的接触定义为 “tie”。

管状子弹撞击入射杆凸台，在入射杆中产生拉伸波，拉伸波透过试件接头Ⅰ对试件加载，由于试件的力学特性与杆材料不同，所以一部分入射杆反射进入入射杆形成反射波，其余部分进入透射杆产生透射波。模拟计算结果如图10所示，分别为入射杆和透射杆的中点处获得入射波、反射波和透射波的波形图，入射波和反射波相加获得计算透射波的值。

从图10中可以看出入射波和反射波之和获得的计算透射波信号与透射杆上的透射波一致，满足Hopkinson杆实验的试件应力均匀假设。

3 结束语

基于应力波理论和分离式霍普金森实验技术，对30mm SHTB装置的拉伸波生成方式和试件连接方式进行改进。改进后的装置模型加工和装配更加简单；试件的加工和装夹更加便捷，缩短了高应变率拉伸实验周期；能够满足软质复合材料高应变率实验要求并且由于试件的缩短而使得应变率提高。

图10 模拟真实试件 （线性粘弹性本构）

基于ABAQUS显式算法数值仿真技术对改进后的模型进行仿真研究，研究结果表明，改进后的装置模型满足SHTB实验一维应力波假设和试件应力均匀假设。数值仿真结果为较大杆径SHTB装置的改进设计和实验提供了理论基础。

［1］Lim A S，Lopatnikov S L，Gillespie J W.Development of the split－Hopkinson pressure bar technique for viscous fluid characterization［J］.Polymer Testing，2009，28 （8）：891－900.

［2］Ramírez H，Rubio－Gonzalez C.Finite－element simulation of wave propagation and dispersion in Hopkinson bar test［J］.Materials ＆Design，2006，27 （1）：36－44.

［3］ZANG Xiaowei.Study on the pulse shaping technique and a programming implementation for data processing of the Hopkinson bar experiments［D］.Nanjing：Nanjing University of Science and Technology，2010：15－46 （in Chinese）.［臧小为.霍普金森压杆过载波形整形及系统分析软件研究 ［D］.南京：南京理 工大学，2010：15－46.］

［4］FENG Ping，ZHANG Qingming，CHEN Yao.Influence of incident pulse of slope on stress uniformity and constant strain rate in SHPB test［J］.Transactions of Beijing Institute of Technology，2010，30 （5）：513－516 （in Chinese）. ［丰平，张庆明，陈姚.SHPB测试中斜坡加载对应力均匀性和恒应变率的影响分析 ［J］.北京理工大学学报，2010，30 （5）：513－516.］

［5］JIAO Chujie，JIANG Guoping，GAO Le，et al.Numerical simulation on impact resistance of steel fiber reinforced high strength concrete［J］.Journal of Jiangsu University（Natural Science Edition），2012，33 （3）：350－353 （in Chinese）. ［焦楚杰，蒋国平，高乐，等.钢纤维高强混凝土抗冲击性能的数值仿真［J］.江苏大学学报（自然科学版），2012，33 （3）：350－353.］

［6］Aleyaasin M，Harrigan J J.Wave dispersion and attenuation in viscoelastic polymeric bars：Analysing the effect of lateral inertia［J］.International Journal of Mechanical Sciences，2010，52（5）：754－757.

［7］Dai F，Huang S，Xia K W，et al.Some fundamental issues in dynamic compression and tension tests of rocks using split hopkinson pressure bar［J］.Rock Mechanics and Rock Engineering，2010，43 （6）：657－666.

［8］Wang Q Z，Li W，Xie H P.Dynamic split tensile test of flattened brazilian disc of rock with SHPB setup［J］.Mechanics of Materials，2009，41 （3）：252－260.

［9］Fu S Q，Wang Y，Wang Y.Tension testing of polycarbonate at high strain rates ［J］.Polymer Testing，2009，28 （7）：724－729.

［10］Sun X，Soulami A，Choi K S，et al.Effects of sample geometry and loading rate on tensile ductility of TRIP800steel［J］.Materials Science and Engineering A，2012，541：1－7.

［11］Meng Honglei.Research on numerical simulation method of structure integrity analysis for modified double base propellant grain［D］.Nanjing：Nanjing University of Science and Technology，2011：29－34 （in Chinese）. ［孟红磊.改性双基推进剂装药结构完整性数值仿真方法研究 ［D］.南京：南京理工大学，2011：29－34.］